No CrossRef data available.
Article contents
The number of maximum primitive sets of integers
Published online by Cambridge University Press: 28 January 2021
Abstract
A set of integers is primitive if it does not contain an element dividing another. Let f(n) denote the number of maximum-size primitive subsets of {1,…,2n}. We prove that the limit α = limn→∞f(n)1/n exists. Furthermore, we present an algorithm approximating α with (1 + ε) multiplicative error in N(ε) steps, showing in particular that α ≈ 1.318. Our algorithm can be adapted to estimate the number of all primitive sets in {1,…,n} as well.
We address another related problem of Cameron and Erdős. They showed that the number of sets containing pairwise coprime integers in {1,…n} is between 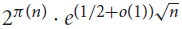 ${2^{\pi (n)}} \cdot {e^{(1/2 + o(1))\sqrt n }}$ and
${2^{\pi (n)}} \cdot {e^{(1/2 + o(1))\sqrt n }}$ and 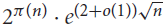 ${2^{\pi (n)}} \cdot {e^{(2 + o(1))\sqrt n }}$. We show that neither of these bounds is tight: there are in fact
${2^{\pi (n)}} \cdot {e^{(2 + o(1))\sqrt n }}$. We show that neither of these bounds is tight: there are in fact 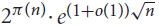 ${2^{\pi (n)}} \cdot {e^{(1 + o(1))\sqrt n }}$ such sets.
${2^{\pi (n)}} \cdot {e^{(1 + o(1))\sqrt n }}$ such sets.
MSC classification
Information
- Type
- Paper
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
Footnotes
Supported partly by the UK Research and Innovation Future Leaders Fellowship MR/S016325/1 and the Leverhulme Trust Early Career Fellowship ECF-2016-523.
Partially supported by the National Research, Development and Innovation Office NKFIH (grant PD115978 and BME NC TKP2020), the Lendület program and the János Bolyai Research Scholarship of the Hungarian Academy of Sciences. He has also received funding from the European Research Council (ERC) under the European Union’s Horizon 2020 research and innovation programme (grant agreement 648509). This publication reflects only its author’s view; the European Research Council Executive Agency is not responsible for any use that may be made of the information it contains.
Supported by the Lendület program of the Hungarian Academy of Sciences (MTA) and the BME-Artificial Intelligence FIKP grant of EMMI (BME FIKP-MI/SC).


