No CrossRef data available.
Article contents
On a conjecture of Conlon, Fox, and Wigderson
Published online by Cambridge University Press: 16 February 2024
Abstract
For graphs 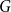 $G$ and
$G$ and 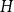 $H$, the Ramsey number
$H$, the Ramsey number 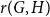 $r(G,H)$ is the smallest positive integer
$r(G,H)$ is the smallest positive integer 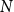 $N$ such that any red/blue edge colouring of the complete graph
$N$ such that any red/blue edge colouring of the complete graph 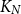 $K_N$ contains either a red
$K_N$ contains either a red 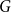 $G$ or a blue
$G$ or a blue 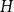 $H$. A book
$H$. A book 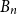 $B_n$ is a graph consisting of
$B_n$ is a graph consisting of  $n$ triangles all sharing a common edge.
$n$ triangles all sharing a common edge.
Recently, Conlon, Fox, and Wigderson conjectured that for any 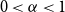 $0\lt \alpha \lt 1$, the random lower bound
$0\lt \alpha \lt 1$, the random lower bound 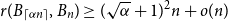 $r(B_{\lceil \alpha n\rceil },B_n)\ge (\sqrt{\alpha }+1)^2n+o(n)$ is not tight. In other words, there exists some constant
$r(B_{\lceil \alpha n\rceil },B_n)\ge (\sqrt{\alpha }+1)^2n+o(n)$ is not tight. In other words, there exists some constant 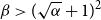 $\beta \gt (\sqrt{\alpha }+1)^2$ such that
$\beta \gt (\sqrt{\alpha }+1)^2$ such that 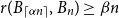 $r(B_{\lceil \alpha n\rceil },B_n)\ge \beta n$ for all sufficiently large
$r(B_{\lceil \alpha n\rceil },B_n)\ge \beta n$ for all sufficiently large  $n$. This conjecture holds for every
$n$. This conjecture holds for every 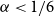 $\alpha \lt 1/6$ by a result of Nikiforov and Rousseau from 2005, which says that in this range
$\alpha \lt 1/6$ by a result of Nikiforov and Rousseau from 2005, which says that in this range 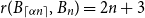 $r(B_{\lceil \alpha n\rceil },B_n)=2n+3$ for all sufficiently large
$r(B_{\lceil \alpha n\rceil },B_n)=2n+3$ for all sufficiently large  $n$.
$n$.
We disprove the conjecture of Conlon, Fox, and Wigderson. Indeed, we show that the random lower bound is asymptotically tight for every 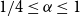 $1/4\leq \alpha \leq 1$. Moreover, we show that for any
$1/4\leq \alpha \leq 1$. Moreover, we show that for any 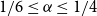 $1/6\leq \alpha \le 1/4$ and large
$1/6\leq \alpha \le 1/4$ and large  $n$,
$n$, 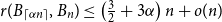 $r(B_{\lceil \alpha n\rceil }, B_n)\le \left (\frac 32+3\alpha \right ) n+o(n)$, where the inequality is asymptotically tight when
$r(B_{\lceil \alpha n\rceil }, B_n)\le \left (\frac 32+3\alpha \right ) n+o(n)$, where the inequality is asymptotically tight when 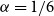 $\alpha =1/6$ or
$\alpha =1/6$ or 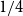 $1/4$. We also give a lower bound of
$1/4$. We also give a lower bound of 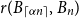 $r(B_{\lceil \alpha n\rceil }, B_n)$ for
$r(B_{\lceil \alpha n\rceil }, B_n)$ for 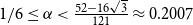 $1/6\le \alpha \lt \frac{52-16\sqrt{3}}{121}\approx 0.2007$, showing that the random lower bound is not tight, i.e., the conjecture of Conlon, Fox, and Wigderson holds in this interval.
$1/6\le \alpha \lt \frac{52-16\sqrt{3}}{121}\approx 0.2007$, showing that the random lower bound is not tight, i.e., the conjecture of Conlon, Fox, and Wigderson holds in this interval.
MSC classification
Information
- Type
- Paper
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press
Footnotes
Supported in part by National Key R&D Program of China (Grant No. 2023YFA1010202), NSFC (No. 12171088, 12226401) and NSFFJ (No. 2022J02018).


