Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Brightwell, Graham R.
and
Winkler, Peter
2009.
Submodular Percolation.
SIAM Journal on Discrete Mathematics,
Vol. 23,
Issue. 3,
p.
1149.
Basu, Riddhipratim
Sidoravicius, Vladas
and
Sly, Allan
2019.
Sojourns in Probability Theory and Statistical Physics - III.
Vol. 300,
Issue. ,
p.
90.
Bates, Erik
and
Podder, Moumanti
2021.
Avoidance couplings on non‐complete graphs.
Random Structures & Algorithms,
Vol. 59,
Issue. 1,
p.
25.

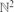 be
be 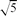 )/2.
)/2.