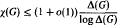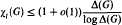Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kahn, Jeff
and
Kayll, P.Mark
1997.
Fractional v. Integral Covers in Hypergraphs of Bounded Edge Size.
Journal of Combinatorial Theory, Series A,
Vol. 78,
Issue. 2,
p.
199.
Kahn, Jeff
1997.
The Mathematics of Paul Erdös I.
Vol. 13,
Issue. ,
p.
345.
Molloy, Michael
1998.
Probabilistic Methods for Algorithmic Discrete Mathematics.
Vol. 16,
Issue. ,
p.
1.
McDiarmid, Colin
1998.
Probabilistic Methods for Algorithmic Discrete Mathematics.
Vol. 16,
Issue. ,
p.
195.
Vu, Van H.
1999.
On some simple degree conditions that guarantee the upper bound on the chromatic (choice) number of random graphs.
Journal of Graph Theory,
Vol. 31,
Issue. 3,
p.
201.
Kahn, Jeff
2000.
Asymptotics of the list-chromatic index for multigraphs.
Random Structures and Algorithms,
Vol. 17,
Issue. 2,
p.
117.
Grable, David A
and
Panconesi, Alessandro
2000.
Fast Distributed Algorithms for Brooks–Vizing Colorings.
Journal of Algorithms,
Vol. 37,
Issue. 1,
p.
85.
Mahdian, Mohammad
2000.
The strong chromatic index ofC4-free graphs.
Random Structures and Algorithms,
Vol. 17,
Issue. 3-4,
p.
357.
Molloy, Michael
and
Reed, Bruce
2000.
k-Colouring when k is close to Δ.
Electronic Notes in Discrete Mathematics,
Vol. 5,
Issue. ,
p.
235.
Kim, Jeong Han
2001.
Nearly Optimal Partial Steiner Systems.
Electronic Notes in Discrete Mathematics,
Vol. 7,
Issue. ,
p.
74.
Stacho, Ladislav
2001.
New upper bounds for the chromatic number of a graph.
Journal of Graph Theory,
Vol. 36,
Issue. 2,
p.
117.
Vu, Van H.
2001.
Some recent results on list coloring.
Electronic Notes in Discrete Mathematics,
Vol. 7,
Issue. ,
p.
170.
Amit, Alon
Linial, Nathan
and
Matoušek, Jiří
2002.
Random lifts of graphs: Independence and chromatic number.
Random Structures & Algorithms,
Vol. 20,
Issue. 1,
p.
1.
Vu, V. H.
2002.
Concentration of non‐Lipschitz functions and applications.
Random Structures & Algorithms,
Vol. 20,
Issue. 3,
p.
262.
Kim, Jeong Han
and
Lee, Sungchul
2003.
Tail bound for the minimal spanning tree of a complete graph.
Statistics & Probability Letters,
Vol. 64,
Issue. 4,
p.
425.
Kim, J. H.
and
Vu, V. H.
2004.
Divide and conquer martingales and the number of triangles in a random graph.
Random Structures & Algorithms,
Vol. 24,
Issue. 2,
p.
166.
Łuczak, Tomasz
and
Vigoda, Eric
2005.
Torpid mixing of the Wang–Swendsen–Kotecký algorithm for sampling colorings.
Journal of Discrete Algorithms,
Vol. 3,
Issue. 1,
p.
92.
Bayati, Mohsen
Kim, Jeong Han
and
Saberi, Amin
2007.
Approximation, Randomization, and Combinatorial Optimization. Algorithms and Techniques.
Vol. 4627,
Issue. ,
p.
326.
Randerath, Bert
and
Schiermeyer, Ingo
2007.
Graph Theory in Paris.
p.
339.
Hefetz, Dan
Krivelevich, Michael
Stojaković, Miloš
and
Szabó, Tibor
2008.
Planarity, Colorability, and Minor Games.
SIAM Journal on Discrete Mathematics,
Vol. 22,
Issue. 1,
p.
194.