Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T17:02:55.644Z Has data issue: false hasContentIssue false
  • English
  • Français

On convex holes in d-dimensional point sets

Part of: Discrete geometry Probabilistic theory: distribution modulo $1$; metric theory of algorithms

Published online by Cambridge University Press:  18 June 2021

Boris Bukh ,
Ting-Wei Chao  and
Ron Holzman
Boris Bukh*
Affiliation:
Department of Mathematical Sciences, Carnegie Mellon University, Pittsburgh, PA15213, USA
Ting-Wei Chao
Affiliation:
Department of Mathematical Sciences, Carnegie Mellon University, Pittsburgh, PA15213, USA
Ron Holzman
Affiliation:
Department of Mathematics, Technion-Israel Institute of Technology, Haifa3200003, Israel
*
*Corresponding author. Email: bbukh@math.cmu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a finite set 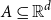$A \subseteq \mathbb{R}^d$, points 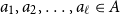$a_1,a_2,\dotsc,a_{\ell} \in A$ form an 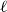$\ell$-hole in A if they are the vertices of a convex polytope, which contains no points of A in its interior. We construct arbitrarily large point sets in general position in 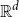$\mathbb{R}^d$ having no holes of size 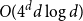$O(4^dd\log d)$ or more. This improves the previously known upper bound of order 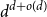$d^{d+o(d)}$ due to Valtr. The basic version of our construction uses a certain type of equidistributed point sets, originating from numerical analysis, known as (t,m,s)-nets or (t,s)-sequences, yielding a bound of 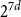$2^{7d}$. The better bound is obtained using a variant of (t,m,s)-nets, obeying a relaxed equidistribution condition.

Keywords

convex holesErdős–Szekeres theorem(t,m,s)-nets

MSC classification

Primary: 52C10: Erdős problems and related topics of discrete geometry
Secondary: 11K38: Irregularities of distribution, discrepancy
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 31 , Issue 1 , January 2022 , pp. 101 - 108
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Supported in part by US taxpayers through NSF CAREER grant DMS-1555149.

‡

Work done during a visit at the Department of Mathematics, Princeton University, supported by the H2020-MSCARISE project CoSP–GA No. 823748.

References

Aichholzer, O., Balko, M., Hackl, T., KynČl, J., Parada, I., Scheucher, M., Valtr, P. and Vogtenhuber, B. (2020) A superlinear lower bound on the number of 5-holes. J. Combin. Theory Ser. A 173 105236, 31. arXiv:1703.05253.CrossRefGoogle Scholar
BÁrÁny, I. and FÜredi, Z. (1987) Empty simplices in Euclidean space. Canad. Math. Bull. 30(4) 436–445. https://faculty.math.illinois.edu/ z-furedi/PUBS/furedi_barany_empty-simplices.pdf.CrossRefGoogle Scholar
Bukh, B. and Chao, T.-W. (2021) Digital almost nets. arXiv:2102.12872.Google Scholar
ErdÖs, P. (1975) On some problems of elementary and combinatorial geometry. Ann. Mat. Pura Appl. (4) 103 99–108. https://users.renyi.hu/ p_erdos/1975-25.pdf.CrossRefGoogle Scholar
ErdÖs, P. and Szekeres, G. (1935) A combinatorial problem in geometry. Compositio Math. 2 463–470.Google Scholar
Gerken, T. (2008) Empty convex hexagons in planar point sets. Discrete Comput. Geom. 39(1–3) 239–272.CrossRefGoogle Scholar
Harborth, H. (1978) Konvexe FÜnfecke in ebenen Punktmengen. Elem. Math. 33(5) 116–118. doi: 10.5169/seals-32945.Google Scholar
Horton, J. D. (1983) Sets with no empty convex 7-gons. Canad. Math. Bull. 26(4) 482–484.CrossRefGoogle Scholar
Katchalski, M. and Meir, A. (1988) On empty triangles determined by points in the plane. Acta Math. Hungar. 51(3–4) 323–328.CrossRefGoogle Scholar
NicolÁs, C. M. (2007) The empty hexagon theorem. Discrete Comput. Geom. 38(2) 389–397.CrossRefGoogle Scholar
Niederreiter, H. and Xing, C. (1996) Low-discrepancy sequences and global function fields with many rational places. Finite Fields Appl. 2(3) 241–273.CrossRefGoogle Scholar
SchÜrer, R. (2008) A new lower bound on the t-parameter of (t,s)-sequences. In Monte Carlo and quasi-Monte Carlo methods 2006, Springer, Berlin, pp. 623–632.CrossRefGoogle Scholar
Sobol’, I. M. (1967) Distribution of points in a cube and approximate evaluation of integrals. Ž. VyČisl. Mat i Mat. Fiz. 7 784–802. http://mi.mathnet.ru/zvmmf7334.Google Scholar
Valtr, P. (1992) Sets in ${\bf R}^d$ with no large empty convex subsets. Discrete Math. 108(1–3) 115–124. Topological, algebraical and combinatorial structures. Frolk’s memorial volume.CrossRefGoogle Scholar
Xing, C. P. and Niederreiter, H. (1995) A construction of low-discrepancy sequences using global function fields. Acta Arith. 73(1) 87–102.CrossRefGoogle Scholar