Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T18:35:03.540Z Has data issue: false hasContentIssue false
  • English
  • Français

On Komlós’ tiling theorem in random graphs

Part of: Graph theory

Published online by Cambridge University Press:  25 July 2019

Rajko Nenadov  and
Nemanja Škorić
Rajko Nenadov*
Affiliation:
Department of Mathematics, Monash University, ETH Zurich, 8092 Zürich, Switzerland
Nemanja Škorić
Affiliation:
Institute of Theoretical Computer Science, ETH Zurich, 8092 Zürich, Switzerland, Email: nskoric@inf.ethz.ch
*
*Corresponding author. Email: rajkon@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Given graphs G and H, a family of vertex-disjoint copies of H in G is called an H-tiling. Conlon, Gowers, Samotij and Schacht showed that for a given graph H and a constant γ>0, there exists C>0 such that if 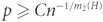$p \ge C{n^{ - 1/{m_2}(H)}}$ , then asymptotically almost surely every spanning subgraph G of the random graph 𝒢(n, p) with minimum degree at least

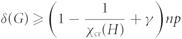$\delta (G) \ge (1 - \frac{1}{{{\chi _{{\rm{cr}}}}(H)}} + \gamma )np$
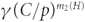contains an H-tiling that covers all but at most γn vertices. Here, χcr(H) denotes the critical chromatic number, a parameter introduced by Komlós, and m2(H) is the 2-density of H. We show that this theorem can be bootstrapped to obtain an H-tiling covering all but at most $\gamma {(C/p)^{{m_2}(H)}}$ vertices, which is strictly smaller when 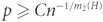$p \ge C{n^{ - 1/{m_2}(H)}}$ . In the case where H = K3, this answers the question of Balogh, Lee and Samotij. Furthermore, for an arbitrary graph H we give an upper bound on p for which some leftover is unavoidable and a bound on the size of a largest H -tiling for p below this value.

MSC classification

Primary: 05C80: Random graphs
Secondary: 05C35: Extremal problems
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 29 , Issue 1 , January 2020 , pp. 113 - 127
Copyright
© Cambridge University Press 2019 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Allen, P., Böttcher, J., Ehrenmüller, J. and Taraz, A. (2015) Local resilience of spanning subgraphs in sparse random graphs. Electron. Notes Discrete Math. 49 513–521.CrossRefGoogle Scholar
Allen, P., Böttcher, J., Hàn, H., Kohayakawa, Y. and Person, Y. (2016) Blow-up lemmas for sparse graphs. arXiv:1612.00622Google Scholar
Alon, N. and Yuster, R. (1992) Almost H-factors in dense graphs. Graphs Combin . 8 95–102.CrossRefGoogle Scholar
Alon, N. and Yuster, R. (1996) H-factors in dense graphs. J. Combin. Theory Ser. B 66 269–282.CrossRefGoogle Scholar
Balogh, J., Lee, C. and Samotij, W. (2012) Corrádi and Hajnal’s theorem for sparse random graphs. Combin. Probab. Comput. 21 23–55.CrossRefGoogle Scholar
Balogh, J., Morris, R. and Samotij, W. (2015) Independent sets in hypergraphs. J. Amer. Math. Soc. 28 669–709.CrossRefGoogle Scholar
Conlon, D., Gowers, W., Samotij, W. and Schacht, M. (2014) On the KŁR conjecture in random graphs. Israel J. Math . 203 535–580.CrossRefGoogle Scholar
Corrádi, K. and Hajnal, A. (1963) On the maximal number of independent circuits in a graph. Acta Math. Acad. Sci. Hungar. 14 423–439.CrossRefGoogle Scholar
Erdös, P. and Rényi, A. (1960) On the evolution of random graphs. Magyar Tud. Akad. Mat. Kutató Int. Közl. 5 17–61.Google Scholar
Gerke, S. and McDowell, A. (2015) Nonvertex-balanced factors in random graphs. J. Graph Theory 78 269–286.CrossRefGoogle Scholar
Hajnal, A. and Szemerédi, E. (1970) Proof of a conjecture of P. Erdös. In Combinatorial Theory and its Applications, II (Proc. Colloq., Balatonfüred, 1969), North-Holland, pp. 601–623.Google Scholar
Huang, H., Lee, C. and Sudakov, B. (2012) Bandwidth theorem for random graphs. J. Combin. Theory Ser. B 102 14–37.CrossRefGoogle Scholar
Johansson, A., Kahn, J. and Vu, V. (2008) Factors in random graphs. Random Struct. Alg . 33 1–28.CrossRefGoogle Scholar
Kim, J. H. and Vu, V. H. (2000) Concentration of multivariate polynomials and its applications. Combinatorica 20 417–434.CrossRefGoogle Scholar
Kohayakawa, Y. (1997) Szemerédi’s regularity lemma for sparse graphs. In Foundations of Computational Mathematics, Springer, pp. 216–230.CrossRefGoogle Scholar
Kohayakawa, Y., Łuczak, T. and Rödl, V. (1997) On K 4-free subgraphs of random graphs. Combinatorica 17 173–213.CrossRefGoogle Scholar
Komlós, J. (2000) Tiling Turán theorems. Combinatorica 20 203–218.Google Scholar
Komlós, J., Sárközy, G. and Szemerédi, E. (2001) Proof of the Alon–Yuster conjecture. Discrete Math . 235 255–269.CrossRefGoogle Scholar
Kühn, D. and Osthus, D. (2009) Embedding large subgraphs into dense graphs. In Surveys in Combinatorics 2009, Vol. 365 of London Mathematical Society Lecture Note Series, Cambridge University Press, pp. 137–167.CrossRefGoogle Scholar
Kühn, D. and Osthus, D. (2009) The minimum degree threshold for perfect graph packings. Combinatorica 29 65–107.CrossRefGoogle Scholar
Saxton, D. and Thomason, A. (2015) Hypergraph containers. Inventio. Math. 201 925–992.CrossRefGoogle Scholar
Shokoufandeh, A. and Zhao, Y. (2003) Proof of a tiling conjecture of Komlós. Random Struct. Alg . 23 180–205.CrossRefGoogle Scholar