Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-28T03:43:38.098Z Has data issue: false hasContentIssue false
  • English
  • Français

On minimal Ramsey graphs and Ramsey equivalence in multiple colours

Part of: Extremal combinatorics

Published online by Cambridge University Press:  09 March 2020

Dennis Clemens ,
Anita Liebenau  and
Damian Reding
Dennis Clemens
Affiliation:
Institut für Mathematik, Technische Universität Hamburg, 21073Hamburg, Germany
Anita Liebenau*
Affiliation:
School of Mathematics and Statistics, UNSW Sydney, SydneyNSW2052, Australia
*
*Corresponding author. Email: a.liebenau@unsw.edu.au
Get access Rights & Permissions [Opens in a new window]

Abstract

For an integer q ⩾ 2, a graph G is called q-Ramsey for a graph H if every q-colouring of the edges of G contains a monochromatic copy of H. If G is q-Ramsey for H yet no proper subgraph of G has this property, then G is called q-Ramsey-minimal for H. Generalizing a statement by Burr, Nešetřil and Rödl from 1977, we prove that, for q ⩾ 3, if G is a graph that is not q-Ramsey for some graph H, then G is contained as an induced subgraph in an infinite number of q-Ramsey-minimal graphs for H as long as H is 3-connected or isomorphic to the triangle. For such H, the following are some consequences.

  • For 2 ⩽ r < q, every r-Ramsey-minimal graph for H is contained as an induced subgraph in an infinite number of q-Ramsey-minimal graphs for H.

  • For every q ⩾ 3, there are q-Ramsey-minimal graphs for H of arbitrarily large maximum degree, genus and chromatic number.

  • The collection 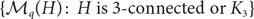$\{\mathcal M_q(H) \colon H \text{ is 3-connected or } K_3\}$ forms an antichain with respect to the subset relation, where 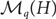$\mathcal M_q(H)$ denotes the set of all graphs that are q-Ramsey-minimal for H.

We also address the question of which pairs of graphs satisfy 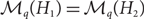$\mathcal M_q(H_1)=\mathcal M_q(H_2)$ , in which case H1 and H2 are called q-equivalent. We show that two graphs H1 and H2 are q-equivalent for even q if they are 2-equivalent, and that in general q-equivalence for some q ⩾ 3 does not necessarily imply 2-equivalence. Finally we indicate that for connected graphs this implication may hold: results by Nešetřil and Rödl and by Fox, Grinshpun, Liebenau, Person and Szabó imply that the complete graph is not 2-equivalent to any other connected graph. We prove that this is the case for an arbitrary number of colours.

MSC classification

Primary: 05D10: Ramsey theory
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 29 , Issue 4 , July 2020 , pp. 537 - 554
Check for updates
Copyright
© Cambridge University Press 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Supported by an ARC Decra Fellowship. Previously at Monash University where this research was partly carried out.

References

Axenovich, M., Rollin, J. and Ueckerdt, T. (2017) Conditions on Ramsey nonequivalence. J. Graph Theory 86 159–192.Google Scholar
Balister, P., Lehel, J. and Schelp, R. (2006) Ramsey unsaturated and saturated graphs. J. Graph Theory 51 22–32.CrossRefGoogle Scholar
Bloom, T. and Liebenau, A. (2018) Ramsey equivalence of Kn and Kn + Kn-1. Electron. J. Combin. 25 P3.4.Google Scholar
Bodkin, C. (2016) Folkman numbers and a conjecture in Ramsey theory. Master’s thesis, FU Berlin.Google Scholar
Bollobás, B., Donadelli, J., Kohayakawa, Y. and Schelp, R. (2001) Ramsey minimal graphs. J. Brazil. Comput. Soc. 7 27–37.CrossRefGoogle Scholar
Burr, S., Erdős, P., Faudree, R., Rousseau, C. and Schelp, R. (1981) Ramsey-minimal graphs for star-forests. Discrete Math. 33 227–237.Google Scholar
Burr, S., Erdős, P. and Lovász, L. (1976) On graphs of Ramsey type. Ars Combin. 1 167–190.Google Scholar
Burr, S., Faudree, R. and Schelp, R. (1977) On Ramsey-minimal graphs. In Proc. 8th Southeastern Conference on Combinatorics, Graph Theory and Computing, pp. 115–124.Google Scholar
Burr, S., Nešetřil, J. and Rödl, V. (1985) On the use of senders in generalized Ramsey theory for graphs. Discrete Math. 54 1–13.Google Scholar
Conlon, D. (2009) A new upper bound for diagonal Ramsey numbers. Ann. of Math. 170 941–960.Google Scholar
Erdős, P. (1947) Some remarks on the theory of graphs. Bull. Amer. Math. Soc. 53 292–294.CrossRefGoogle Scholar
Erdős, P. and Szekeres, G. (1935) A combinatorial problem in geometry. Compositio Math. 2 463–470.Google Scholar
Faudree, R. (2018) Ramsey minimal graphs for forests. Ars Combin 31 117–124.Google Scholar
Folkman, J. (1970) Graphs with monochromatic complete subgraphs in every edge coloring. SIAM J. Appl. Math. 18 19–24.Google Scholar
Fox, J., Grinshpun, A., Liebenau, A., Person, Y. and Szabó, T. (2014) What is Ramsey-equivalent to a clique? J. Combin. Theory Ser. B 109 120–133.Google Scholar
Fox, J., Grinshpun, A., Liebenau, A., Person, Y. and Szabó, T. (2016) On the minimum degree of minimal Ramsey graphs for multiple colours. J. Combin. Theory Ser. B 120 64–82.Google Scholar
Fox, J. and Lin, K. (2006) The minimum degree of Ramsey-minimal graphs. J. Graph Theory 54 167–177.CrossRefGoogle Scholar
Graham, R. and Rödl, V. (1987) Numbers in Ramsey theory. Surveys Combin. 123 111–153.Google Scholar
Guo, H. and Warnke, L. (2020) Packing nearly optimal Ramsey R(3, t) graphs. https://doi.org/10.1007/s00493-019-3921-7 CrossRefGoogle Scholar
Hàn, H., Rödl, V. and Szabó, T. (2018) Vertex Folkman numbers and the minimum degree of minimal Ramsey graphs. SIAM J. Discrete Math. 32 826–838.CrossRefGoogle Scholar
Lin, S. (1972) On Ramsey numbers and K r -coloring of graphs. J. Combin. Theory Ser. B 12 82–92.CrossRefGoogle Scholar
Łuczak, T. (1994) On Ramsey minimal graphs. Electron. J. Combin 1 R4.CrossRefGoogle Scholar
Nešetřil, J. and Rödl, V. (1976) The Ramsey property for graphs with forbidden complete subgraphs. J. Combin. Theory Ser. B 20 243–249.Google Scholar
Ramsey, F. (1930) On a problem of formal logic. Proc. London Math. Soc. 30 264–286.CrossRefGoogle Scholar
Rödl, V. and Ruciński, A. (1995) Threshold functions for Ramsey properties. J. Amer. Math. Soc. 8 917–942.CrossRefGoogle Scholar
Rödl, V. and Siggers, M. (2008) On Ramsey minimal graphs. SIAM J. Discrete Math. 22 467–488.CrossRefGoogle Scholar
Spencer, J. (1977) Asymptotic lower bounds for Ramsey functions. Discrete Math. 20 69–76.CrossRefGoogle Scholar
Szabó, T., Zumstein, P. and Zürcher, S. (2010) On the minimum degree of minimal Ramsey graphs. J. Graph Theory 64 150–164.Google Scholar
Thomason, A. (1988) An upper bound for some Ramsey numbers. J. Graph Theory 12 509–517.CrossRefGoogle Scholar