Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ahlswede, R.
and
Cai, N.
2006.
General Theory of Information Transfer and Combinatorics.
Vol. 4123,
Issue. ,
p.
979.
Hellmuth, Marc
Ostermeier, Lydia
and
Stadler, Peter F.
2012.
A Survey on Hypergraph Products.
Mathematics in Computer Science,
Vol. 6,
Issue. 1,
p.
1.
Leader, Imre
Milićević, Luka
and
Tan, Ta Sheng
2018.
Decomposing the complete r-graph.
Journal of Combinatorial Theory, Series A,
Vol. 154,
Issue. ,
p.
21.
Althöfer, Ingo
Boche, Holger
Deppe, Christian
Tamm, Ulrich
Winter, Andreas
and
Yeung, Raymond W.
2025.
Information Theory and Related Fields.
Vol. 14620,
Issue. ,
p.
505.
Tamm, Ulrich
2025.
Information Theory and Related Fields.
Vol. 14620,
Issue. ,
p.
274.

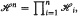 where ℋ
where ℋ
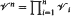 into sets that are elements of
into sets that are elements of  . The main result was that
. The main result was that
