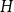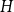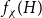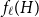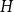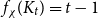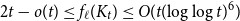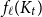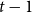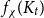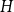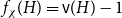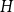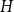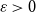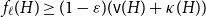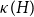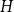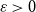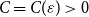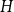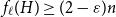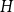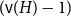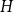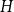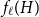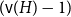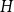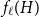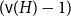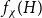1. Introduction
All graphs considered in this paper are finite, have no loops and no parallel edges. Given graphs
![]() $G$
and
$G$
and
![]() $H$
, we say that
$H$
, we say that
![]() $G$
contains
$G$
contains
![]() $H$
as a minor, in symbols,
$H$
as a minor, in symbols,
![]() $G\succeq H$
, if a graph isomorphic to
$G\succeq H$
, if a graph isomorphic to
![]() $H$
can be obtained from a subgraph of
$H$
can be obtained from a subgraph of
![]() $G$
by contracting edges.
$G$
by contracting edges.
Hadwiger’s colouring conjecture, first stated in 1943 by Hugo Hadwiger [Reference Hadwiger8], is among the most famous and important open problems in graph theory. It claims a deep relationship between the chromatic number of graphs and their containment of graph minors, as follows.
Conjecture 1 (Hadwiger [Reference Hadwiger8]). Let
![]() $t \in \mathbb{N}$
. If a graph
$t \in \mathbb{N}$
. If a graph
![]() $G$
is
$G$
is
![]() $K_t$
-minor-free, then
$K_t$
-minor-free, then
![]() $\chi (G)\le t-1$
.
$\chi (G)\le t-1$
.
Hadwiger’s conjecture has been proved for all values
![]() $t \le 6$
, see [Reference Robertson, Seymour and Thomas26] for the most recent result in this sequence, resolving the
$t \le 6$
, see [Reference Robertson, Seymour and Thomas26] for the most recent result in this sequence, resolving the
![]() $K_6$
-minor-free case. For
$K_6$
-minor-free case. For
![]() $t=5$
, the conjecture states that
$t=5$
, the conjecture states that
![]() $K_5$
-minor-free graphs are
$K_5$
-minor-free graphs are
![]() $4$
-colorable. Since planar graphs are
$4$
-colorable. Since planar graphs are
![]() $K_5$
-minor-free, this special case already generalises the famous four colour theorem that was proved in 1976 by Appel, Haken and Koch [Reference Appel and Haken1, Reference Appel, Haken and Koch2].
$K_5$
-minor-free, this special case already generalises the famous four colour theorem that was proved in 1976 by Appel, Haken and Koch [Reference Appel and Haken1, Reference Appel, Haken and Koch2].
Given that during 80 years of study little progress has been made towards resolving Hadwiger’s conjecture for
![]() $t \ge 7$
, it seems natural to approach the conjecture via meaningful relaxations. For instance, much of recent work has focused on its asymptotic version. The so-called linear Hadwiger conjecture states that for some absolute constant
$t \ge 7$
, it seems natural to approach the conjecture via meaningful relaxations. For instance, much of recent work has focused on its asymptotic version. The so-called linear Hadwiger conjecture states that for some absolute constant
![]() $C\ge 1$
, every
$C\ge 1$
, every
![]() $K_t$
-minor-free graph is
$K_t$
-minor-free graph is
![]() $\lfloor Ct \rfloor$
-colorable. Starting with a breakthrough result by Norin, Postle and Song [Reference Norin, Postle and Song20] in 2019, there has been a set of papers providing some exciting progress towards this conjecture [Reference Norin and Postle21, Reference Postle23–Reference Postle25]. This culminated in the currently best known upper bound of
$\lfloor Ct \rfloor$
-colorable. Starting with a breakthrough result by Norin, Postle and Song [Reference Norin, Postle and Song20] in 2019, there has been a set of papers providing some exciting progress towards this conjecture [Reference Norin and Postle21, Reference Postle23–Reference Postle25]. This culminated in the currently best known upper bound of
![]() $O(t \log \log t)$
for the chromatic number of
$O(t \log \log t)$
for the chromatic number of
![]() $K_t$
-minor-free graphs by Delcourt and Postle [Reference Delcourt and Postle6] in 2021.
$K_t$
-minor-free graphs by Delcourt and Postle [Reference Delcourt and Postle6] in 2021.
Another natural relaxation, proposed by Seymour [Reference Seymour27, Reference Seymour28], suggests replacing the condition that the considered graphs exclude
![]() $K_t$
as a minor by the stronger condition that they exclude a particular, possibly non-complete graph
$K_t$
as a minor by the stronger condition that they exclude a particular, possibly non-complete graph
![]() $H$
on
$H$
on
![]() $t$
vertices as a minor.
$t$
vertices as a minor.
Conjecture 2 (
![]() $H$
-Hadwiger’s conjecture [Reference Seymour27, Reference Seymour28]).
$H$
-Hadwiger’s conjecture [Reference Seymour27, Reference Seymour28]).
![]() $H$
-minor-free graphs are
$H$
-minor-free graphs are
![]() $({\textrm{v}}(H)-1)$
-colorable.
$({\textrm{v}}(H)-1)$
-colorable.
Note that Hadwiger’s conjecture would imply the truth of this statement for every
![]() $H$
. Also note that this upper bound on the chromatic number would be best possible for every
$H$
. Also note that this upper bound on the chromatic number would be best possible for every
![]() $H$
, as the complete graph
$H$
, as the complete graph
![]() $K_{{\textrm{v}}(H)-1}$
has chromatic number
$K_{{\textrm{v}}(H)-1}$
has chromatic number
![]() ${\textrm{v}}(H)-1$
but is too small to host an
${\textrm{v}}(H)-1$
but is too small to host an
![]() $H$
-minor.
$H$
-minor.
![]() $H$
-Hadwiger’s conjecture can easily be verified using a degeneracy-colouring approach if
$H$
-Hadwiger’s conjecture can easily be verified using a degeneracy-colouring approach if
![]() $H$
is a forest, and it is also known to be true for spanning subgraphs of the Petersen graph [Reference Hendrey and Wood9]. A particular case of
$H$
is a forest, and it is also known to be true for spanning subgraphs of the Petersen graph [Reference Hendrey and Wood9]. A particular case of
![]() $H$
-Hadwiger’s conjecture which has received special attention in the past is when
$H$
-Hadwiger’s conjecture which has received special attention in the past is when
![]() $H=K_{s,t}$
is a complete bipartite graph. Woodall [Reference Woodall37] conjectured in 2001 that every
$H=K_{s,t}$
is a complete bipartite graph. Woodall [Reference Woodall37] conjectured in 2001 that every
![]() $K_{s,t}$
-minor-free graph is
$K_{s,t}$
-minor-free graph is
![]() $(s+t-1)$
-colorable. Also this problem remains open, but if true it would resolve
$(s+t-1)$
-colorable. Also this problem remains open, but if true it would resolve
![]() $H$
-Hadwiger’s conjecture for all bipartite
$H$
-Hadwiger’s conjecture for all bipartite
![]() $H$
. Several special cases of this conjecture have been solved by now. Most notably, Kostochka [Reference Kostochka14, Reference Kostochka15] proved that for some function
$H$
. Several special cases of this conjecture have been solved by now. Most notably, Kostochka [Reference Kostochka14, Reference Kostochka15] proved that for some function
![]() $t_0(s)=O(s^3\log ^3 s)$
,
$t_0(s)=O(s^3\log ^3 s)$
,
![]() $H$
-Hadwiger’s conjecture holds whenever
$H$
-Hadwiger’s conjecture holds whenever
![]() $H=K_{s,t}$
and
$H=K_{s,t}$
and
![]() $t \ge t_0(s)$
. The conjecture is also true for
$t \ge t_0(s)$
. The conjecture is also true for
![]() $H=K_{3,3}$
, which can be seen using the structure theorem for
$H=K_{3,3}$
, which can be seen using the structure theorem for
![]() $K_{3,3}$
-minor-free graphs by Wagner [Reference Wagner35] and the fact that planar graphs are
$K_{3,3}$
-minor-free graphs by Wagner [Reference Wagner35] and the fact that planar graphs are
![]() $5$
-colorable. In addition, the statement has been proved for
$5$
-colorable. In addition, the statement has been proved for
![]() $H=K_{2,t}$
when
$H=K_{2,t}$
when
![]() $t \ge 1$
[Reference Chudnovsky, Reed and Seymour5, Reference Myers18, Reference Woodall37, Reference Woodall38], for
$t \ge 1$
[Reference Chudnovsky, Reed and Seymour5, Reference Myers18, Reference Woodall37, Reference Woodall38], for
![]() $H=K_{3,t}$
when
$H=K_{3,t}$
when
![]() $t \ge 6300$
[Reference Kostochka and Prince16] and for
$t \ge 6300$
[Reference Kostochka and Prince16] and for
![]() $H=K_{3,4}$
[Reference Jørgensen10]. In a different direction, Norin and Turcotte [Reference Norin and Turcotte22] recently proved
$H=K_{3,4}$
[Reference Jørgensen10]. In a different direction, Norin and Turcotte [Reference Norin and Turcotte22] recently proved
![]() $H$
-Hadwiger’s conjecture for all sufficiently large bipartite graphs of bounded maximum degree that belong to a class of graphs with strongly sublinear separators.
$H$
-Hadwiger’s conjecture for all sufficiently large bipartite graphs of bounded maximum degree that belong to a class of graphs with strongly sublinear separators.
1.1. List colouring
 $H$
-minor-free graphs
$H$
-minor-free graphs
In this paper, we shall be concerned with the list chromatic number of graphs that exclude a fixed graph
![]() $H$
as a minor. List colouring is a well-known and popular subject in the area of graph colouring, whose introduction dates back to the seminal paper of Erdős, Rubin and Taylor [Reference Erdős, Rubin and Taylor7]. A list assignment for a graph
$H$
as a minor. List colouring is a well-known and popular subject in the area of graph colouring, whose introduction dates back to the seminal paper of Erdős, Rubin and Taylor [Reference Erdős, Rubin and Taylor7]. A list assignment for a graph
![]() $G$
is a mapping
$G$
is a mapping
![]() $L:V(G)\rightarrow 2^{\mathbb{N}}$
assigning to every vertex
$L:V(G)\rightarrow 2^{\mathbb{N}}$
assigning to every vertex
![]() $v \in V(G)$
a finite set
$v \in V(G)$
a finite set
![]() $L(v)$
of colours, also called the list of
$L(v)$
of colours, also called the list of
![]() $v$
. An
$v$
. An
![]() $L$
-colouring of
$L$
-colouring of
![]() $G$
is a proper colouring
$G$
is a proper colouring
![]() $c:V(G)\rightarrow \mathbb{N}$
for which every vertex must choose a colour from its list, that is,
$c:V(G)\rightarrow \mathbb{N}$
for which every vertex must choose a colour from its list, that is,
![]() $c(v) \in L(v)$
for every
$c(v) \in L(v)$
for every
![]() $v \in V(G)$
. Finally, we say that
$v \in V(G)$
. Finally, we say that
![]() $G$
is
$G$
is
![]() $k$
-choosable for some integer
$k$
-choosable for some integer
![]() $k \ge 1$
if there exists a proper
$k \ge 1$
if there exists a proper
![]() $L$
-colouring for every list assignment
$L$
-colouring for every list assignment
![]() $L$
satisfying
$L$
satisfying
![]() $|L(v)|\ge k$
for all
$|L(v)|\ge k$
for all
![]() $v \in V(G)$
. The list chromatic number of
$v \in V(G)$
. The list chromatic number of
![]() $G$
, denoted
$G$
, denoted
![]() $\chi _\ell (G)$
, is the smallest integer
$\chi _\ell (G)$
, is the smallest integer
![]() $k$
such that
$k$
such that
![]() $G$
is
$G$
is
![]() $k$
-choosable. Note that trivially
$k$
-choosable. Note that trivially
![]() $\chi (G)\le \chi _\ell (G)$
for every graph
$\chi (G)\le \chi _\ell (G)$
for every graph
![]() $G$
, but conversely no relationship holds, as
$G$
, but conversely no relationship holds, as
![]() $\chi _\ell (G)$
is unbounded even on bipartite graphs
$\chi _\ell (G)$
is unbounded even on bipartite graphs
![]() $G$
, see [Reference Erdős, Rubin and Taylor7].
$G$
, see [Reference Erdős, Rubin and Taylor7].
The first open problem regarding list colouring of minor-closed graph classes was raised already in 1979 in the seminal paper by Erdős, Rubin and Taylor [Reference Erdős, Rubin and Taylor7], who asked to determine the maximum list chromatic number of planar graphs. This question was answered in the 1990s in work of Thomassen [Reference Thomassen33] and Voigt [Reference Voigt34]. Thomassen proved that every planar graph is
![]() $5$
-choosable, and Voigt gave the first examples of planar graphs
$5$
-choosable, and Voigt gave the first examples of planar graphs
![]() $G$
with list chromatic number
$G$
with list chromatic number
![]() $\chi _\ell (G)=5$
.
$\chi _\ell (G)=5$
.
The latter result also answered a question by Borowiecki [Reference Borowiecki4] in the negative, who had asked whether one could potentially strengthen Hadwiger’s conjecture to the list colouring setting by asserting that every
![]() $K_t$
-minor-free graph
$K_t$
-minor-free graph
![]() $G$
satisfies
$G$
satisfies
![]() $\chi _\ell (G)\le t-1$
.
$\chi _\ell (G)\le t-1$
.
Given the previous discussion, it is natural to study the maximum list chromatic number of
![]() $K_t$
-minor-free graphs, see also [39] for an open problem garden entry about this problem. To make the following presentation more convenient, for every graph
$K_t$
-minor-free graphs, see also [39] for an open problem garden entry about this problem. To make the following presentation more convenient, for every graph
![]() $H$
we denote by
$H$
we denote by
![]() $f_\chi (H)$
and
$f_\chi (H)$
and
![]() $f_\ell (H)$
, respectively, the maximum (list) chromatic number of
$f_\ell (H)$
, respectively, the maximum (list) chromatic number of
![]() $H$
-minor-free graphs. Note that with this notation, the
$H$
-minor-free graphs. Note that with this notation, the
![]() $H$
-Hadwiger’s conjecture amounts to saying that
$H$
-Hadwiger’s conjecture amounts to saying that
![]() $f_\chi (H)={\textrm{v}}(H)-1$
.
$f_\chi (H)={\textrm{v}}(H)-1$
.
Let us briefly summarise previous work regarding bounds on
![]() $f_\ell (K_t)$
. The construction of Voigt mentioned above shows that
$f_\ell (K_t)$
. The construction of Voigt mentioned above shows that
![]() $f_\ell (K_5)\ge 5$
. Thomassen’s result regarding the
$f_\ell (K_5)\ge 5$
. Thomassen’s result regarding the
![]() $5$
-choosability of planar graphs was later extended by Škrekovski [Reference Škrekovski29] to
$5$
-choosability of planar graphs was later extended by Škrekovski [Reference Škrekovski29] to
![]() $K_5$
-minor-free graphs, thus proving that
$K_5$
-minor-free graphs, thus proving that
![]() $f_\ell (K_5)=5$
. Until today none of the values
$f_\ell (K_5)=5$
. Until today none of the values
![]() $f_\ell (K_t)$
with
$f_\ell (K_t)$
with
![]() $t \ge 6$
have been determined precisely, a list of the currently best known lower and upper bounds for
$t \ge 6$
have been determined precisely, a list of the currently best known lower and upper bounds for
![]() $f_\ell (K_t)$
for small values of
$f_\ell (K_t)$
for small values of
![]() $t$
can be found in [Reference Barát, Joret and Wood3]. In 2007, Kawarabayashi and Mohar [Reference Kawarabayashi and Mohar12] made two conjectures regarding the asymptotic behaviour of
$t$
can be found in [Reference Barát, Joret and Wood3]. In 2007, Kawarabayashi and Mohar [Reference Kawarabayashi and Mohar12] made two conjectures regarding the asymptotic behaviour of
![]() $f_\ell (K_t)$
, namely that (A)
$f_\ell (K_t)$
, namely that (A)
![]() $f_\ell (K_t)=O(t)$
, this is known as the list linear Hadwiger conjecture, and that (B)
$f_\ell (K_t)=O(t)$
, this is known as the list linear Hadwiger conjecture, and that (B)
![]() $f_\ell (K_t)\le \frac{3}{2}t$
for every
$f_\ell (K_t)\le \frac{3}{2}t$
for every
![]() $t$
. In 2010, Wood [Reference Wood36], inspired by the fact that
$t$
. In 2010, Wood [Reference Wood36], inspired by the fact that
![]() $f_\ell (K_5)=5$
, proposed an even stronger conjecture stating that
$f_\ell (K_5)=5$
, proposed an even stronger conjecture stating that
![]() $f_\ell (K_t)=t$
for every
$f_\ell (K_t)=t$
for every
![]() $t \ge 5$
. This strong conjecture was refuted in 2011 by Barát, Joret and Wood, who gave a construction showing that
$t \ge 5$
. This strong conjecture was refuted in 2011 by Barát, Joret and Wood, who gave a construction showing that
![]() $f_\ell (K_t) \ge \frac{4}{3}t-O(1)$
. However, the weaker conjecture (B) by Kawarabayashi and Mohar still remained open. Recently, a new lower bound of
$f_\ell (K_t) \ge \frac{4}{3}t-O(1)$
. However, the weaker conjecture (B) by Kawarabayashi and Mohar still remained open. Recently, a new lower bound of
![]() $f_\ell (K_t) \ge 2t-o(t)$
was established by the second author [Reference Steiner30], thus refuting conjecture (B). As for upper bounds, the best currently known bound is
$f_\ell (K_t) \ge 2t-o(t)$
was established by the second author [Reference Steiner30], thus refuting conjecture (B). As for upper bounds, the best currently known bound is
![]() $f_\ell (K_t) \le Ct (\!\log \log t)^6$
, which was established in 2020 by Postle [Reference Postle25]. Some previous work also addressed bounds on
$f_\ell (K_t) \le Ct (\!\log \log t)^6$
, which was established in 2020 by Postle [Reference Postle25]. Some previous work also addressed bounds on
![]() $f_\ell (H)$
when
$f_\ell (H)$
when
![]() $H$
is non-complete. In particular, Woodall [Reference Seymour27] conjectured in 2001 that
$H$
is non-complete. In particular, Woodall [Reference Seymour27] conjectured in 2001 that
![]() $f_\ell (K_{s,t})=s+t-1$
for all integers
$f_\ell (K_{s,t})=s+t-1$
for all integers
![]() $s, t \ge 1$
, and proved this in the case when
$s, t \ge 1$
, and proved this in the case when
![]() $s=t=3$
. From the previously mentioned works [Reference Chudnovsky, Reed and Seymour5, Reference Myers18, Reference Woodall37, Reference Woodall38] it was also known that
$s=t=3$
. From the previously mentioned works [Reference Chudnovsky, Reed and Seymour5, Reference Myers18, Reference Woodall37, Reference Woodall38] it was also known that
![]() $f_\ell (K_{2,t})=t+1$
for
$f_\ell (K_{2,t})=t+1$
for
![]() $t \ge 1$
. Additionally, a result by Jørgensen [Reference Jørgensen10] implied the truth of the conjecture for
$t \ge 1$
. Additionally, a result by Jørgensen [Reference Jørgensen10] implied the truth of the conjecture for
![]() $K_{3,4}$
, and Kawarabayashi [Reference Kawarabayashi11] proved that
$K_{3,4}$
, and Kawarabayashi [Reference Kawarabayashi11] proved that
![]() $f_\ell (K_{4,t})\le 4t$
for every
$f_\ell (K_{4,t})\le 4t$
for every
![]() $t$
. Despite this positive evidence, Woodall’s conjecture was recently disproved by the second author [Reference Steiner31] showing that
$t$
. Despite this positive evidence, Woodall’s conjecture was recently disproved by the second author [Reference Steiner31] showing that
![]() $f_\ell (K_{s,t})\ge (1-o(1))( 2s+t)$
for all large values of
$f_\ell (K_{s,t})\ge (1-o(1))( 2s+t)$
for all large values of
![]() $s \le t$
. A positive result comes from the aforementioned result of Norin and Turcotte [Reference Norin and Turcotte22], which also works for list colourings and shows that
$s \le t$
. A positive result comes from the aforementioned result of Norin and Turcotte [Reference Norin and Turcotte22], which also works for list colourings and shows that
![]() $f_\ell (H)={\textrm{v}}(H)-1$
for all large bipartite graphs
$f_\ell (H)={\textrm{v}}(H)-1$
for all large bipartite graphs
![]() $H$
of bounded maximum degree in a graph class with strongly sublinear separators.
$H$
of bounded maximum degree in a graph class with strongly sublinear separators.
1.2. Our contribution
The above discussion shows that when excluding a sufficiently large complete or a sufficiently large balanced complete bipartite graph
![]() $H$
, the value of
$H$
, the value of
![]() $f_\ell (H)$
exceeds the trivial lower bound
$f_\ell (H)$
exceeds the trivial lower bound
![]() $f_\ell (H) \ge{\textrm{v}}(H)-1$
by at least a constant factor. This means that, in a strong sense, one cannot hope for extending Hadwiger’s conjecture to list colouring with the same quantitative bounds. However, note that if
$f_\ell (H) \ge{\textrm{v}}(H)-1$
by at least a constant factor. This means that, in a strong sense, one cannot hope for extending Hadwiger’s conjecture to list colouring with the same quantitative bounds. However, note that if
![]() $H$
is a complete or a balanced complete bipartite graph, then
$H$
is a complete or a balanced complete bipartite graph, then
![]() $H$
is quite dense in the sense that it has a quadratic number of edges. On the other extreme of the spectrum, the previously mentioned result by Norin and Turcotte [Reference Norin and Turcotte22] shows that
$H$
is quite dense in the sense that it has a quadratic number of edges. On the other extreme of the spectrum, the previously mentioned result by Norin and Turcotte [Reference Norin and Turcotte22] shows that
![]() $f_\ell (H)={\textrm{v}}(H)-1$
does hold for large classes of graphs
$f_\ell (H)={\textrm{v}}(H)-1$
does hold for large classes of graphs
![]() $H$
with a constant maximum degree (and thus, with a linear number of edges). This naturally opens up a new question, as follows: How sparse must the desired minor
$H$
with a constant maximum degree (and thus, with a linear number of edges). This naturally opens up a new question, as follows: How sparse must the desired minor
![]() $H$
be, such that one can hope for a list colouring extension of
$H$
be, such that one can hope for a list colouring extension of
![]() $H$
-Hadwiger’s conjecture? Concretely, which structural and density properties of graphs
$H$
-Hadwiger’s conjecture? Concretely, which structural and density properties of graphs
![]() $H$
guarantee that
$H$
guarantee that
![]() $f_\ell (H)={\textrm{v}}(H)-1$
? While one might be tempted to hope for a nice description of the class of all graphs
$f_\ell (H)={\textrm{v}}(H)-1$
? While one might be tempted to hope for a nice description of the class of all graphs
![]() $H$
satisfying
$H$
satisfying
![]() $f_\ell (H)={\textrm{v}}(H)-1$
, Theorem 3 below speaks a word of caution: Any given graph
$f_\ell (H)={\textrm{v}}(H)-1$
, Theorem 3 below speaks a word of caution: Any given graph
![]() $F$
can be augmented, by the addition of sufficiently many isolated vertices, to a graph
$F$
can be augmented, by the addition of sufficiently many isolated vertices, to a graph
![]() $H$
in this class.
$H$
in this class.
Theorem 3.
For every graph
![]() $F$
there exists
$F$
there exists
![]() $k_0=k_0(F)$
such that for every
$k_0=k_0(F)$
such that for every
![]() $k \ge k_0$
the graph
$k \ge k_0$
the graph
![]() $H$
obtained from
$H$
obtained from
![]() $F$
by the addition of
$F$
by the addition of
![]() $k$
isolated vertices satisfies
$k$
isolated vertices satisfies
![]() $f_\ell (H)={\textrm{v}}(H)-1$
. In fact, every
$f_\ell (H)={\textrm{v}}(H)-1$
. In fact, every
![]() $H$
-minor-free graph is
$H$
-minor-free graph is
![]() $({\textrm{v}}(H)-2)$
-degenerate.
$({\textrm{v}}(H)-2)$
-degenerate.
This shows that arbitrary graphs
![]() $F$
can show up as induced subgraphs of graphs
$F$
can show up as induced subgraphs of graphs
![]() $H$
with
$H$
with
![]() $f_\ell (H)={\textrm{v}}(H)-1$
. To avoid such artificial constructions and to make a nice structural description of the graph class at hand more likely, it seems natural to ask for the largest class that is closed under taking subgraphs such that all members
$f_\ell (H)={\textrm{v}}(H)-1$
. To avoid such artificial constructions and to make a nice structural description of the graph class at hand more likely, it seems natural to ask for the largest class that is closed under taking subgraphs such that all members
![]() $H$
of this class satisfy
$H$
of this class satisfy
![]() $f_\ell (H)={\textrm{v}}(H)-1$
.Footnote
1
$f_\ell (H)={\textrm{v}}(H)-1$
.Footnote
1
Problem 4.
Characterise the class
![]() $\mathcal{H}$
of graphs
$\mathcal{H}$
of graphs
![]() $H$
such that
$H$
such that
![]() $f_\ell (H')={\textrm{v}}(H')-1$
for all
$f_\ell (H')={\textrm{v}}(H')-1$
for all
![]() $H'\subseteq H$
.
$H'\subseteq H$
.
The main contributions of this paper are Theorems 5 and 7 below, which establish new lower bounds on
![]() $f_\ell (H)$
and strongly limit the horizon for positive instances of Problem 4. The first result proves a lower bound on
$f_\ell (H)$
and strongly limit the horizon for positive instances of Problem 4. The first result proves a lower bound on
![]() $f_\ell (H)$
in terms of
$f_\ell (H)$
in terms of
![]() ${\textrm{v}}(H)$
and the vertex-connectivity
${\textrm{v}}(H)$
and the vertex-connectivity
![]() $\kappa (H)$
, implying that
$\kappa (H)$
, implying that
![]() $f_\ell (H)$
exceeds
$f_\ell (H)$
exceeds
![]() ${\textrm{v}}(H)$
by a constant factor for all large graphs of linear connectivity.Footnote
2
${\textrm{v}}(H)$
by a constant factor for all large graphs of linear connectivity.Footnote
2
Theorem 5.
For every
![]() $\varepsilon \gt 0$
there exists
$\varepsilon \gt 0$
there exists
![]() $n_0=n_0(\varepsilon )\in \mathbb{N}$
such that every graph
$n_0=n_0(\varepsilon )\in \mathbb{N}$
such that every graph
![]() $H$
on at least
$H$
on at least
![]() $n_0$
vertices satisfies
$n_0$
vertices satisfies
![]() $f_\ell (H)\ge (1-\varepsilon )({\textrm{v}}(H)+\kappa (H))$
.
$f_\ell (H)\ge (1-\varepsilon )({\textrm{v}}(H)+\kappa (H))$
.
In particular, this result immediately generalises both of the lower bounds of
![]() $f_\ell (K_t)\ge 2t-o(t)$
and
$f_\ell (K_t)\ge 2t-o(t)$
and
![]() $f_\ell (K_{s,t})\ge (1-o(1))(2s+t)$
previously established by the second author in [Reference Steiner30, Reference Steiner31] by noting that
$f_\ell (K_{s,t})\ge (1-o(1))(2s+t)$
previously established by the second author in [Reference Steiner30, Reference Steiner31] by noting that
![]() $\kappa (K_t)=t-1$
and
$\kappa (K_t)=t-1$
and
![]() $\kappa (K_{s,t})=s$
for
$\kappa (K_{s,t})=s$
for
![]() $s \le t$
. It also has the following simple consequence, showing that the graphs in
$s \le t$
. It also has the following simple consequence, showing that the graphs in
![]() $\mathcal{H}$
have a subquadratic number of edges.
$\mathcal{H}$
have a subquadratic number of edges.
Corollary 6.
For every
![]() $n \in \mathbb{N}$
, let
$n \in \mathbb{N}$
, let
![]() $h(n)$
denote the maximum possible number of edges of an
$h(n)$
denote the maximum possible number of edges of an
![]() $n$
-vertex graph in
$n$
-vertex graph in
![]() $\mathcal{H}$
. Then
$\mathcal{H}$
. Then
![]() $\lim _{n\rightarrow \infty }\frac{h(n)}{n^2}=0$
.
$\lim _{n\rightarrow \infty }\frac{h(n)}{n^2}=0$
.
Proof. Towards a contradiction, suppose the statement is not true. Then there is some constant
![]() $\delta \gt 0$
such that there exist arbitrarily large graphs
$\delta \gt 0$
such that there exist arbitrarily large graphs
![]() $H \in \mathcal{H}$
with average degree at least
$H \in \mathcal{H}$
with average degree at least
![]() $\delta{\textrm{v}}(H)$
. By a classical result of Mader [Reference Mader17], every graph of average degree at least
$\delta{\textrm{v}}(H)$
. By a classical result of Mader [Reference Mader17], every graph of average degree at least
![]() $4(k-1)$
for some integer
$4(k-1)$
for some integer
![]() $k \ge 2$
contains a
$k \ge 2$
contains a
![]() $k$
-connected subgraph. As
$k$
-connected subgraph. As
![]() $\mathcal{H}$
is closed under subgraphs, this implies that there are arbitrarily large graphs
$\mathcal{H}$
is closed under subgraphs, this implies that there are arbitrarily large graphs
![]() $H \in \mathcal{H}$
with connectivity at least
$H \in \mathcal{H}$
with connectivity at least
![]() $\frac{\delta }{4}{\textrm{v}}(H)$
. Then, using
$\frac{\delta }{4}{\textrm{v}}(H)$
. Then, using
![]() $\varepsilon \;:\!=\; \frac{\delta }{8}$
and Theorem 5, for sufficiently large
$\varepsilon \;:\!=\; \frac{\delta }{8}$
and Theorem 5, for sufficiently large
![]() $H \in \mathcal{H}$
with average degree at least
$H \in \mathcal{H}$
with average degree at least
![]() $\delta{\textrm{v}}(H)$
, we have
$\delta{\textrm{v}}(H)$
, we have
![]() $f_\ell (H) \geq (1-\varepsilon )(1+\frac{\delta }{4}){\textrm{v}}(H) = (1+\frac{\delta }{8}-\frac{\delta ^2}{32}){\textrm{v}}(H) \gt{\textrm{v}}(H)$
. However, we have
$f_\ell (H) \geq (1-\varepsilon )(1+\frac{\delta }{4}){\textrm{v}}(H) = (1+\frac{\delta }{8}-\frac{\delta ^2}{32}){\textrm{v}}(H) \gt{\textrm{v}}(H)$
. However, we have
![]() $f_\ell (H) ={\textrm{v}}(H)-1$
by the definition of
$f_\ell (H) ={\textrm{v}}(H)-1$
by the definition of
![]() $\mathcal{H}$
, which yields the desired contradiction and concludes the proof.
$\mathcal{H}$
, which yields the desired contradiction and concludes the proof.
Our second result addresses to what extent sparsity of
![]() $H$
can push
$H$
can push
![]() $f_\ell (H)$
closer to the trivial lower bound
$f_\ell (H)$
closer to the trivial lower bound
![]() ${\textrm{v}}(H)-1$
, by showing that for any fixed
${\textrm{v}}(H)-1$
, by showing that for any fixed
![]() $\varepsilon \gt 0$
, asymptotically almost all
$\varepsilon \gt 0$
, asymptotically almost all
![]() $n$
-vertex graphs
$n$
-vertex graphs
![]() $H$
with average degree of order
$H$
with average degree of order
![]() $C\log n$
for a sufficiently large constant
$C\log n$
for a sufficiently large constant
![]() $C$
are far from being in
$C$
are far from being in
![]() $\mathcal{H}$
, in the sense that
$\mathcal{H}$
, in the sense that
![]() $f_\ell (H)$
is separated from
$f_\ell (H)$
is separated from
![]() ${\textrm{v}}(H)-1$
by a factor of at least
${\textrm{v}}(H)-1$
by a factor of at least
![]() $2-\varepsilon$
.
$2-\varepsilon$
.
Theorem 7.
For every
![]() $\varepsilon \gt 0$
there exists a constant
$\varepsilon \gt 0$
there exists a constant
![]() $C=C(\varepsilon )\gt 0$
such that asymptotically almost every graph
$C=C(\varepsilon )\gt 0$
such that asymptotically almost every graph
![]() $H$
on
$H$
on
![]() $n$
vertices with
$n$
vertices with
![]() $\lceil C n\log n \rceil$
edges satisfies
$\lceil C n\log n \rceil$
edges satisfies
![]() $f_\ell (H)\ge (2-\varepsilon ) n$
.
$f_\ell (H)\ge (2-\varepsilon ) n$
.
Together with Corollary 6, this hints at the graphs in
![]() $\mathcal{H}$
typically being quite sparse. It also shows that the lower bound
$\mathcal{H}$
typically being quite sparse. It also shows that the lower bound
![]() $f_\ell (K_t)\ge 2t-o(t)$
for complete graphs from [Reference Steiner30] applies in equal strength to almost all
$f_\ell (K_t)\ge 2t-o(t)$
for complete graphs from [Reference Steiner30] applies in equal strength to almost all
![]() $t$
-vertex graphs
$t$
-vertex graphs
![]() $H$
with
$H$
with
![]() $\omega (t \log t)$
edges, despite them being (much) sparser than
$\omega (t \log t)$
edges, despite them being (much) sparser than
![]() $K_t$
.
$K_t$
.
Our proofs of Theorems 5 and 7 are based on several extensions and refinements of the probabilistic approach for lower bounding
![]() $f_\ell (K_t)$
and
$f_\ell (K_t)$
and
![]() $f_\ell (K_{s,t})$
introduced by the second author in [Reference Steiner30, Reference Steiner31]. However, several new ideas are required to overcome obstacles arising from the largely increased generality of the setup. For instance, to prove Theorem 7 one has to construct graphs avoiding rather sparse graphs
$f_\ell (K_{s,t})$
introduced by the second author in [Reference Steiner30, Reference Steiner31]. However, several new ideas are required to overcome obstacles arising from the largely increased generality of the setup. For instance, to prove Theorem 7 one has to construct graphs avoiding rather sparse graphs
![]() $H$
as a minor. While the constructions in [Reference Steiner30, Reference Steiner31] were based on the fact that clique sums of graphs under mild assumptions preserve
$H$
as a minor. While the constructions in [Reference Steiner30, Reference Steiner31] were based on the fact that clique sums of graphs under mild assumptions preserve
![]() $K_t$
- and
$K_t$
- and
![]() $K_{s,t}$
-minor-freeness, a corresponding statement is no longer true for sparse graphs
$K_{s,t}$
-minor-freeness, a corresponding statement is no longer true for sparse graphs
![]() $H$
of much lower connectivity.
$H$
of much lower connectivity.
1.3. Organisation of the paper
In Section 2 we prove two probabilistic results on random bipartite graphs that exhibit properties of these graphs that are crucial for our constructions in the proofs of Theorems 5 and 7. We then present the proofs of our main results Theorem 5 and Theorem 7 in, respectively, Section 3 and Section 4. Finally, in Section 5 we separately prove Theorem 3. The latter proof is self-contained and independent of the results in the other three sections.
1.4. Notation and terminology
By
![]() $\kappa (G)$
we denote the vertex-connectivity of a graph
$\kappa (G)$
we denote the vertex-connectivity of a graph
![]() $G$
, i.e., the minimum
$G$
, i.e., the minimum
![]() $k$
such that
$k$
such that
![]() $G$
is
$G$
is
![]() $k$
-connected. Given integers
$k$
-connected. Given integers
![]() $m, n \ge 1$
and an edge-probability
$m, n \ge 1$
and an edge-probability
![]() $p \in [0,1]$
, we use
$p \in [0,1]$
, we use
![]() $G(m,n;p)$
to denote the bipartite Erdős-Rényi random graph with bipartition classes
$G(m,n;p)$
to denote the bipartite Erdős-Rényi random graph with bipartition classes
![]() $A$
and
$A$
and
![]() $B$
of sizes
$B$
of sizes
![]() $m$
and
$m$
and
![]() $n$
, respectively, and in which a pair
$n$
, respectively, and in which a pair
![]() $ab$
with
$ab$
with
![]() $a\in A$
and
$a\in A$
and
![]() $b \in B$
is chosen as an edge of
$b \in B$
is chosen as an edge of
![]() $G(m,n;p)$
independently with probability
$G(m,n;p)$
independently with probability
![]() $p$
. For integers
$p$
. For integers
![]() $m, n \ge 1$
we denote by
$m, n \ge 1$
we denote by
![]() $G(n;m)$
a random graph drawn uniformly from all graphs on vertex set
$G(n;m)$
a random graph drawn uniformly from all graphs on vertex set
![]() $[n]=\{1,\ldots,n\}$
with exactly
$[n]=\{1,\ldots,n\}$
with exactly
![]() $m$
edges.
$m$
edges.
While the original definition of the graph minor-containment relation
![]() $\succeq$
is via edge contractions and deletions, for proving the results in this paper it will be more convenient to think about graph minor models. Given a graph
$\succeq$
is via edge contractions and deletions, for proving the results in this paper it will be more convenient to think about graph minor models. Given a graph
![]() $G$
and a graph
$G$
and a graph
![]() $H$
, an
$H$
, an
![]() $H$
-minor model is a collection
$H$
-minor model is a collection
![]() $(Z_h)_{h \in V(H)}$
of pairwise disjoint and non-empty subsets of
$(Z_h)_{h \in V(H)}$
of pairwise disjoint and non-empty subsets of
![]() $V(G)$
with the property that
$V(G)$
with the property that
![]() $G[Z_h]$
is a connected graph for every
$G[Z_h]$
is a connected graph for every
![]() $h \in V(H)$
and such that for every edge
$h \in V(H)$
and such that for every edge
![]() $h_1h_2 \in E(H)$
, there exists at least one edge in
$h_1h_2 \in E(H)$
, there exists at least one edge in
![]() $G$
with endpoints in
$G$
with endpoints in
![]() $Z_{h_1}$
and
$Z_{h_1}$
and
![]() $Z_{h_2}$
. The sets
$Z_{h_2}$
. The sets
![]() $Z_h, h \in V(H)$
are also called the branch sets of the minor model. It is well-known and easy to see that for every pair of graphs
$Z_h, h \in V(H)$
are also called the branch sets of the minor model. It is well-known and easy to see that for every pair of graphs
![]() $G$
and
$G$
and
![]() $H$
we have
$H$
we have
![]() $G \succeq H$
if and only if there exists an
$G \succeq H$
if and only if there exists an
![]() $H$
-minor model in
$H$
-minor model in
![]() $G$
.
$G$
.
2. Probabilistic lemmas
In this short preparatory section we prove two simple auxiliary results (Lemmas 9 and 11) that will be used in the proofs of both our main results in Section 3 and 4. The lemmas capture two simple but important properties exhibited by bipartite Erdős-Rényi random graphs. These properties will later be used to lower bound the list chromatic number of the graphs in our constructions for Theorems 5 and 7 and to argue that they exclude a given graph as a minor.
Two basic tools from probability theory that we will use in the following are the classical Chernoff concentration bounds, stated below. A standard application of the Chernoff bounds yields an upper bound on the maximum degree of bipartite graphs with linear expected degree, stated below without proof.
Lemma 8 (Chernoff). Let
![]() $X$
be a binomially distributed random variable. Then the following bounds hold for every
$X$
be a binomially distributed random variable. Then the following bounds hold for every
![]() $\delta \in (0,1]$
:
$\delta \in (0,1]$
:
Lemma 9.
Let
![]() $p \in (0,1]$
be a constant. Then w.h.p. the random bipartite graph
$p \in (0,1]$
be a constant. Then w.h.p. the random bipartite graph
![]() $G=G(n, n; p)$
has maximum degree at most
$G=G(n, n; p)$
has maximum degree at most
![]() $2pn$
.
$2pn$
.
In order to compactly state and refer to our next lemma below, it is convenient for us to introduce a technical definition for the following relationship between a graph
![]() $H$
and a bipartite graph
$H$
and a bipartite graph
![]() $G$
with vertex bipartition
$G$
with vertex bipartition
![]() $A,B$
. Let
$A,B$
. Let
![]() $G^\complement$
denote the graph complement of
$G^\complement$
denote the graph complement of
![]() $G$
. We are interested in the existence of
$G$
. We are interested in the existence of
![]() $\widetilde{H}$
-minor models in
$\widetilde{H}$
-minor models in
![]() $G^\complement$
, where
$G^\complement$
, where
![]() $\widetilde{H}$
is a subgraph of
$\widetilde{H}$
is a subgraph of
![]() $H$
. For fixed integers
$H$
. For fixed integers
![]() $k,l$
, consider the situation where
$k,l$
, consider the situation where
![]() $X_1, \ldots, X_{k} \subseteq A, Y_1, \ldots, Y_k \subseteq B$
are pairwise disjoint subsets of
$X_1, \ldots, X_{k} \subseteq A, Y_1, \ldots, Y_k \subseteq B$
are pairwise disjoint subsets of
![]() $A$
and
$A$
and
![]() $B$
and
$B$
and
![]() $x_1,\ldots,x_k, y_1, \ldots, y_l \in V(H)$
are distinct vertices of
$x_1,\ldots,x_k, y_1, \ldots, y_l \in V(H)$
are distinct vertices of
![]() $H$
. Let
$H$
. Let
![]() $\widetilde{H}$
be the induced subgraph by the vertices
$\widetilde{H}$
be the induced subgraph by the vertices
![]() $\{x_1,\ldots,x_k, y_1, \ldots, y_l\}$
and let
$\{x_1,\ldots,x_k, y_1, \ldots, y_l\}$
and let
![]() $Z_{x_1} \;:\!=\; X_1, \ldots, Z_{x_k} \;:\!=\; X_k, Z_{y_1} \;:\!=\; Y_1, \ldots, Z_{y_l} \;:\!=\; Y_l$
. Then the branch sets
$Z_{x_1} \;:\!=\; X_1, \ldots, Z_{x_k} \;:\!=\; X_k, Z_{y_1} \;:\!=\; Y_1, \ldots, Z_{y_l} \;:\!=\; Y_l$
. Then the branch sets
![]() $(Z_v)_{v \in V(\widetilde{H})}$
form an
$(Z_v)_{v \in V(\widetilde{H})}$
form an
![]() $\widetilde{H}$
-minor model in
$\widetilde{H}$
-minor model in
![]() $G^\complement$
if and only if each branch set is connected and for each edge of the form
$G^\complement$
if and only if each branch set is connected and for each edge of the form
![]() $x_i y_j \in E(H)$
there is an edge between
$x_i y_j \in E(H)$
there is an edge between
![]() $Z_{x_i}$
and
$Z_{x_i}$
and
![]() $Z_{y_j}$
in
$Z_{y_j}$
in
![]() $G^\complement$
. Therefore,
$G^\complement$
. Therefore,
![]() $(Z_v)_{v \in V(\widetilde{H})}$
is not an
$(Z_v)_{v \in V(\widetilde{H})}$
is not an
![]() $\widetilde{H}$
-minor model in
$\widetilde{H}$
-minor model in
![]() $G^\complement$
if there is an edge
$G^\complement$
if there is an edge
![]() $x_i y_j \in E(H)$
such that
$x_i y_j \in E(H)$
such that
![]() $G$
contains all edges between
$G$
contains all edges between
![]() $X_{i}$
and
$X_{i}$
and
![]() $Y_{j}$
. This relationship, with some additional constraints on branch set size and subgraph size, is captured by the following property.
$Y_{j}$
. This relationship, with some additional constraints on branch set size and subgraph size, is captured by the following property.
Definition 10 (Property
![]() $\textsf{P}$
). Let
$\textsf{P}$
). Let
![]() $0\lt \delta \lt 1$
,
$0\lt \delta \lt 1$
,
![]() $s \in \mathbb{N}$
and let
$s \in \mathbb{N}$
and let
![]() $H$
be a graph on
$H$
be a graph on
![]() $n$
vertices. We say that a bipartite graph
$n$
vertices. We say that a bipartite graph
![]() $G$
with bipartition
$G$
with bipartition
![]() $\{A, B\}$
satisfies property
$\{A, B\}$
satisfies property
![]() $\textsf{P}(H, \delta,s)$
if for all integers
$\textsf{P}(H, \delta,s)$
if for all integers
![]() $k, l \geq \delta n$
the following holds:
$k, l \geq \delta n$
the following holds:
If
![]() $x_1,\ldots,x_k, y_1, \ldots, y_l \in V(H)$
are distinct vertices satisfying
$x_1,\ldots,x_k, y_1, \ldots, y_l \in V(H)$
are distinct vertices satisfying
![]() ${\textrm{e}}_H(\{x_1,\ldots,x_k\},\{y_1,\ldots,y_l\}) \ge s$
and
${\textrm{e}}_H(\{x_1,\ldots,x_k\},\{y_1,\ldots,y_l\}) \ge s$
and
![]() $X_1, \ldots, X_{k} \subseteq A$
,
$X_1, \ldots, X_{k} \subseteq A$
,
![]() $Y_1, \ldots, Y_{l} \subseteq B$
are pairwise disjoint sets of size at most
$Y_1, \ldots, Y_{l} \subseteq B$
are pairwise disjoint sets of size at most
![]() $\frac{1}{\delta }$
each, then there exists an index pair
$\frac{1}{\delta }$
each, then there exists an index pair
![]() $(i,j) \in [k]\times [l]$
such that
$(i,j) \in [k]\times [l]$
such that
![]() $x_iy_j \in E(H)$
and
$x_iy_j \in E(H)$
and
![]() $xy \in E(G)$
for every
$xy \in E(G)$
for every
![]() $(x,y) \in X_i \times Y_j$
.
$(x,y) \in X_i \times Y_j$
.
Lemma 11.
Let
![]() $\delta, p \in (0,1)$
be constants. Then there exists a constant
$\delta, p \in (0,1)$
be constants. Then there exists a constant
![]() $D=D(\delta,p)\gt 1$
and a sequence
$D=D(\delta,p)\gt 1$
and a sequence
![]() $q_n=1-o(1)$
such that with
$q_n=1-o(1)$
such that with
![]() $s=s(n)\;:\!=\;\lceil D n \log n \rceil$
for every
$s=s(n)\;:\!=\;\lceil D n \log n \rceil$
for every
![]() $n$
-vertex graph
$n$
-vertex graph
![]() $H$
the random bipartite graph
$H$
the random bipartite graph
![]() $G = G (n,n;p)$
satisfies
$G = G (n,n;p)$
satisfies
![]() $\textsf{P}(H, \delta,s)$
with probability at least
$\textsf{P}(H, \delta,s)$
with probability at least
![]() $q_n$
.
$q_n$
.
Proof. Choose any constant
![]() $D\gt \max \{1,3p^{-(1/\delta ^2)}\}$
. Let
$D\gt \max \{1,3p^{-(1/\delta ^2)}\}$
. Let
![]() $A, B$
be the vertex bipartition of
$A, B$
be the vertex bipartition of
![]() $G$
with
$G$
with
![]() $|A| = |B| = n$
, let
$|A| = |B| = n$
, let
![]() $H$
be an
$H$
be an
![]() $n$
-vertex graph and let
$n$
-vertex graph and let
![]() $k, l \ge \delta n$
. There are at most
$k, l \ge \delta n$
. There are at most
![]() $n^n$
choices of distinct vertices
$n^n$
choices of distinct vertices
![]() $x_1, \ldots, x_k, y_1, \ldots, y_l \in V(H)$
and at most
$x_1, \ldots, x_k, y_1, \ldots, y_l \in V(H)$
and at most
![]() $n^{2n}$
choices of disjoint vertex sets
$n^{2n}$
choices of disjoint vertex sets
![]() $X_1, \ldots, X_k \subseteq A, \ Y_1, \ldots, Y_l \subseteq B$
. Consider a fixed such choice satisfying the premises in Definition 10 and the random event that for every pair
$X_1, \ldots, X_k \subseteq A, \ Y_1, \ldots, Y_l \subseteq B$
. Consider a fixed such choice satisfying the premises in Definition 10 and the random event that for every pair
![]() $(i,j) \in [k]\times [l]$
such that
$(i,j) \in [k]\times [l]$
such that
![]() $x_iy_j \in E(H)$
, not all of the potential edges between
$x_iy_j \in E(H)$
, not all of the potential edges between
![]() $X_i$
and
$X_i$
and
![]() $Y_j$
are included in
$Y_j$
are included in
![]() $G$
. The probability that this holds is
$G$
. The probability that this holds is
![]() $\prod _{x_iy_j \in E(H)}(1-p^{|X_i||Y_j|}) \leq (1-p^{(1/\delta ^2)})^{Dn\log n}$
, where we used the premises that the sets
$\prod _{x_iy_j \in E(H)}(1-p^{|X_i||Y_j|}) \leq (1-p^{(1/\delta ^2)})^{Dn\log n}$
, where we used the premises that the sets
![]() $X_i, Y_j$
are of size at most
$X_i, Y_j$
are of size at most
![]() $\frac{1}{\delta }$
and that there are at least
$\frac{1}{\delta }$
and that there are at least
![]() $s\ge Dn\log n$
edges of the form
$s\ge Dn\log n$
edges of the form
![]() $x_iy_j\in E(H)$
. Using a union bound over the choices described above, we have
$x_iy_j\in E(H)$
. Using a union bound over the choices described above, we have
 \begin{align*}\mathbb {P}(G\text { does not satisfy property }\textsf {P}(H,\delta,s)) &\le n^{3n} (1-p^{(1/\delta ^2)})^{Dn\log n} \\[5pt] &\le \exp\!(3n\log n - p^{(1/\delta ^2)} Dn\log n).\end{align*}
\begin{align*}\mathbb {P}(G\text { does not satisfy property }\textsf {P}(H,\delta,s)) &\le n^{3n} (1-p^{(1/\delta ^2)})^{Dn\log n} \\[5pt] &\le \exp\!(3n\log n - p^{(1/\delta ^2)} Dn\log n).\end{align*}
We have
![]() $3-p^{(1/\delta ^2)}D\lt 0$
and thus the above expression tends to
$3-p^{(1/\delta ^2)}D\lt 0$
and thus the above expression tends to
![]() $0$
as
$0$
as
![]() $n\rightarrow \infty$
. Setting
$n\rightarrow \infty$
. Setting
![]() $q_n\;:\!=\;1-\exp\!((3-p^{(1/\delta ^2)}D)n\log n)$
then concludes the proof of the lemma.
$q_n\;:\!=\;1-\exp\!((3-p^{(1/\delta ^2)}D)n\log n)$
then concludes the proof of the lemma.
3. Proof of Theorem 5
In this section, we present the proof of Theorem 5. We start off by making use of Lemmas 9 and 11 from the previous section to establish the existence of small
![]() $H$
-minor-free graphs that are in a sense “almost complete”, as follows.
$H$
-minor-free graphs that are in a sense “almost complete”, as follows.
Lemma 12.
For every
![]() $\varepsilon \in (0,\frac{1}{2})$
there exists an integer
$\varepsilon \in (0,\frac{1}{2})$
there exists an integer
![]() $N=N(\varepsilon )$
such that for every
$N=N(\varepsilon )$
such that for every
![]() $n \ge N$
and every
$n \ge N$
and every
![]() $n$
-vertex graph
$n$
-vertex graph
![]() $H$
with
$H$
with
![]() $\kappa (H)\ge \varepsilon n$
there exists a graph
$\kappa (H)\ge \varepsilon n$
there exists a graph
![]() $F$
with the following properties:
$F$
with the following properties:
-
• The vertex set of
 $F$
can be partitioned into two disjoint sets
$F$
can be partitioned into two disjoint sets
 $A$
and
$A$
and
 $B$
such that both
$B$
such that both
 $A$
and
$A$
and
 $B$
form cliques in
$B$
form cliques in
 $F$
and
$F$
and
 $|A|=\lfloor (1-2\varepsilon )\kappa (H)\rfloor$
,
$|A|=\lfloor (1-2\varepsilon )\kappa (H)\rfloor$
,
 $|B|=\lfloor (1-2\varepsilon )n\rfloor$
.
$|B|=\lfloor (1-2\varepsilon )n\rfloor$
. -
• Every vertex in
 $B$
has at most
$B$
has at most
 $\varepsilon n$
non-neighbors in
$\varepsilon n$
non-neighbors in
 $F$
.
$F$
. -
•
 $F$
is
$F$
is
 $H$
-minor-free.
$H$
-minor-free.
Proof. Define
![]() $p\;:\!=\;\frac{\varepsilon }{2}$
and
$p\;:\!=\;\frac{\varepsilon }{2}$
and
![]() $\delta \;:\!=\;\varepsilon ^2$
. By Lemma 9 there is a sequence
$\delta \;:\!=\;\varepsilon ^2$
. By Lemma 9 there is a sequence
![]() $p_n=1-o(1)$
such that
$p_n=1-o(1)$
such that
![]() $G(n,n;p)$
has maximum degree at most
$G(n,n;p)$
has maximum degree at most
![]() $2pn=\varepsilon n$
with probability at least
$2pn=\varepsilon n$
with probability at least
![]() $p_n$
, and by Lemma 11 there exists an absolute constant
$p_n$
, and by Lemma 11 there exists an absolute constant
![]() $D\gt 0$
and a sequence
$D\gt 0$
and a sequence
![]() $q_n=1-o(1)$
such that for every
$q_n=1-o(1)$
such that for every
![]() $n$
-vertex graph
$n$
-vertex graph
![]() $H$
the probability that
$H$
the probability that
![]() $G(n,n;p)$
satisfies property
$G(n,n;p)$
satisfies property
![]() $\textsf{P}(H, \delta, \lceil Dn\log n\rceil )$
is at least
$\textsf{P}(H, \delta, \lceil Dn\log n\rceil )$
is at least
![]() $q_n$
. Let
$q_n$
. Let
![]() $n_1$
be such that
$n_1$
be such that
![]() $p_n, q_n\gt \frac{1}{2}$
for every
$p_n, q_n\gt \frac{1}{2}$
for every
![]() $n \ge n_1$
. Moreover, let
$n \ge n_1$
. Moreover, let
![]() $n_2 \in \mathbb{N}$
be chosen large enough such that the inequality
$n_2 \in \mathbb{N}$
be chosen large enough such that the inequality
![]() $\delta ^2 n^2\ge D n \log n$
holds for every
$\delta ^2 n^2\ge D n \log n$
holds for every
![]() $n \ge n_2$
. Finally, we put
$n \ge n_2$
. Finally, we put
![]() $N\;:\!=\;\max \{n_1,n_2\}$
and let
$N\;:\!=\;\max \{n_1,n_2\}$
and let
![]() $n \geq N$
be arbitrary. By our choice of
$n \geq N$
be arbitrary. By our choice of
![]() $N$
, there then exists at least one bipartite graph
$N$
, there then exists at least one bipartite graph
![]() $G$
with bipartition
$G$
with bipartition
![]() $\{A',B'\}$
such that
$\{A',B'\}$
such that
![]() $|A'|=|B'|=n$
,
$|A'|=|B'|=n$
,
![]() $G$
has maximum degree at most
$G$
has maximum degree at most
![]() $\varepsilon n$
, and
$\varepsilon n$
, and
![]() $G$
satisfies property
$G$
satisfies property
![]() $\textsf{P}(H,\delta, \lceil Dn\log n\rceil )$
. Let
$\textsf{P}(H,\delta, \lceil Dn\log n\rceil )$
. Let
![]() $A \subseteq A', B \subseteq B'$
be chosen (arbitrarily) such that
$A \subseteq A', B \subseteq B'$
be chosen (arbitrarily) such that
![]() $|A|=\lfloor (1-2\varepsilon )\kappa (H)\rfloor$
,
$|A|=\lfloor (1-2\varepsilon )\kappa (H)\rfloor$
,
![]() $|B|=\lfloor (1-2\varepsilon )n\rfloor$
. Note that this is possible as
$|B|=\lfloor (1-2\varepsilon )n\rfloor$
. Note that this is possible as
![]() $\kappa (H)\lt{\textrm{v}}(H)=n$
. We now define
$\kappa (H)\lt{\textrm{v}}(H)=n$
. We now define
![]() $F$
as the graph complement of the induced subgraph
$F$
as the graph complement of the induced subgraph
![]() $G[A \cup B]$
of
$G[A \cup B]$
of
![]() $G$
. Since
$G$
. Since
![]() $A$
and
$A$
and
![]() $B$
are independent sets in
$B$
are independent sets in
![]() $G$
, they form cliques in
$G$
, they form cliques in
![]() $F$
. Thus the first item of the lemma is satisfied. To verify the second item, it suffices to note that since
$F$
. Thus the first item of the lemma is satisfied. To verify the second item, it suffices to note that since
![]() $G$
has maximum degree at most
$G$
has maximum degree at most
![]() $\varepsilon n$
, the same is true for
$\varepsilon n$
, the same is true for
![]() $G[A \cup B]$
, and thus every vertex in
$G[A \cup B]$
, and thus every vertex in
![]() $F$
can have at most
$F$
can have at most
![]() $\varepsilon n$
non-neighbors in
$\varepsilon n$
non-neighbors in
![]() $F$
.
$F$
.
It thus remains to prove that
![]() $F$
is indeed
$F$
is indeed
![]() $H$
-minor-free. Towards a contradiction, suppose that there exists an
$H$
-minor-free. Towards a contradiction, suppose that there exists an
![]() $H$
-minor model
$H$
-minor model
![]() $(Z_h)_{h \in V(H)}$
in
$(Z_h)_{h \in V(H)}$
in
![]() $F$
. Let
$F$
. Let
![]() $X_A, X_B, X_{AB}$
be the partition of
$X_A, X_B, X_{AB}$
be the partition of
![]() $V(H)$
defined as follows:
$V(H)$
defined as follows:
![]() $X_A\;:\!=\;\{h \in V(H)|Z_h \subseteq A\}$
and
$X_A\;:\!=\;\{h \in V(H)|Z_h \subseteq A\}$
and
![]() $X_B\;:\!=\;\{h \in V(H)|Z_h \subseteq B\}$
contain those branch sets which are subsets of
$X_B\;:\!=\;\{h \in V(H)|Z_h \subseteq B\}$
contain those branch sets which are subsets of
![]() $A$
or of
$A$
or of
![]() $B$
, respectively, and
$B$
, respectively, and
![]() $X_{AB}\;:\!=\;\{h \in V(H)|Z_h \cap A \neq \emptyset \neq Z_h \cap B\}$
contains the branch sets which overlap with both
$X_{AB}\;:\!=\;\{h \in V(H)|Z_h \cap A \neq \emptyset \neq Z_h \cap B\}$
contains the branch sets which overlap with both
![]() $A$
and
$A$
and
![]() $B$
.
$B$
.
Our goal now is to find at least
![]() $\delta n$
vertices in
$\delta n$
vertices in
![]() $X_A$
and in
$X_A$
and in
![]() $X_B$
whose corresponding vertex subsets of
$X_B$
whose corresponding vertex subsets of
![]() $A$
or of
$A$
or of
![]() $B$
have size at most
$B$
have size at most
![]() $\frac{1}{\delta }$
and which have at least
$\frac{1}{\delta }$
and which have at least
![]() $D n \log n$
edges between them. We will then be able to use property
$D n \log n$
edges between them. We will then be able to use property
![]() $\textsf{P}(H,\delta,\lceil Dn\log n\rceil )$
to complete the proof.
$\textsf{P}(H,\delta,\lceil Dn\log n\rceil )$
to complete the proof.
Note that we have
![]() $|X_B|+|X_{AB}|\le |B|\le (1-2\varepsilon )n$
as the sets in
$|X_B|+|X_{AB}|\le |B|\le (1-2\varepsilon )n$
as the sets in
![]() $(Z_h)_{h \in V(H)}$
are pairwise disjoint. Given that
$(Z_h)_{h \in V(H)}$
are pairwise disjoint. Given that
![]() $|X_A|+|X_B|+|X_{AB}|={\textrm{v}}(H)=n$
, this implies that
$|X_A|+|X_B|+|X_{AB}|={\textrm{v}}(H)=n$
, this implies that
![]() $|X_A| \ge 2\varepsilon n$
. Since the sets
$|X_A| \ge 2\varepsilon n$
. Since the sets
![]() $(Z_h)_{h \in X_A}$
are disjoint and since
$(Z_h)_{h \in X_A}$
are disjoint and since
![]() $|A|\le (1-2\varepsilon )\kappa (H)\lt (1-2\varepsilon )n\lt n$
, there cannot be more than
$|A|\le (1-2\varepsilon )\kappa (H)\lt (1-2\varepsilon )n\lt n$
, there cannot be more than
![]() $\delta n$
sets of size greater than
$\delta n$
sets of size greater than
![]() $\frac{1}{\delta }$
in the collection
$\frac{1}{\delta }$
in the collection
![]() $(Z_h)_{h \in X_A}$
. Hence, there exists
$(Z_h)_{h \in X_A}$
. Hence, there exists
![]() $k \ge 2\varepsilon n-\delta n\ge \delta n$
and
$k \ge 2\varepsilon n-\delta n\ge \delta n$
and
![]() $k$
distinct vertices
$k$
distinct vertices
![]() $x_1, \ldots,x_k \in X_A$
such that
$x_1, \ldots,x_k \in X_A$
such that
![]() $|Z_{x_i}| \le \frac{1}{\delta }$
for
$|Z_{x_i}| \le \frac{1}{\delta }$
for
![]() $i=1,\ldots,k$
. Note that
$i=1,\ldots,k$
. Note that
![]() $H$
has minimum degree at least
$H$
has minimum degree at least
![]() $\kappa (H)$
, for otherwise one could separate a vertex in
$\kappa (H)$
, for otherwise one could separate a vertex in
![]() $H$
from the rest of the graph by deleting fewer than
$H$
from the rest of the graph by deleting fewer than
![]() $\kappa (H)$
vertices. Using this, we have
$\kappa (H)$
vertices. Using this, we have
for every
![]() $i=1,\ldots,k$
, where in the last step we used that
$i=1,\ldots,k$
, where in the last step we used that
![]() $\kappa (H)\ge \varepsilon n$
by assumption. Consider for any fixed index
$\kappa (H)\ge \varepsilon n$
by assumption. Consider for any fixed index
![]() $i \in [k]$
the set collection
$i \in [k]$
the set collection
![]() $(Z_h)_{h \in N_H(x_i) \cap X_B}$
. Since the sets are pairwise disjoint and contained in the set
$(Z_h)_{h \in N_H(x_i) \cap X_B}$
. Since the sets are pairwise disjoint and contained in the set
![]() $B$
of size at most
$B$
of size at most
![]() $n$
, as above it follows that at most
$n$
, as above it follows that at most
![]() $\delta n$
sets in this collection can be of size greater than
$\delta n$
sets in this collection can be of size greater than
![]() $\frac{1}{\delta }$
. Consequently, for each
$\frac{1}{\delta }$
. Consequently, for each
![]() $i \in [k]$
there exists a subset
$i \in [k]$
there exists a subset
![]() $N_i \subseteq N_H(x_i) \cap X_B$
of size at least
$N_i \subseteq N_H(x_i) \cap X_B$
of size at least
![]() $2\delta n-\delta n=\delta n$
such that
$2\delta n-\delta n=\delta n$
such that
![]() $|Z_h| \le \frac{1}{\delta }$
for every
$|Z_h| \le \frac{1}{\delta }$
for every
![]() $h \in N_i$
and
$h \in N_i$
and
![]() $i \in [k]$
. Let
$i \in [k]$
. Let
![]() $y_1,\ldots,y_l \in X_B$
be distinct vertices such that
$y_1,\ldots,y_l \in X_B$
be distinct vertices such that
![]() $\{y_1,\ldots,y_l\}=\bigcup _{i=1}^{k}{N_i}$
. Then clearly,
$\{y_1,\ldots,y_l\}=\bigcup _{i=1}^{k}{N_i}$
. Then clearly,
![]() $l \ge |N_1|\ge \delta n$
. Furthermore, we have
$l \ge |N_1|\ge \delta n$
. Furthermore, we have
 \begin{equation*}{\textrm {e}}_H(\{x_1,\ldots,x_k\},\{y_1,\ldots,y_l\})\ge \sum _{i=1}^{k}{|N_i|} \ge k\cdot \delta n\ge \delta ^2 n^2\ge D n\log n,\end{equation*}
\begin{equation*}{\textrm {e}}_H(\{x_1,\ldots,x_k\},\{y_1,\ldots,y_l\})\ge \sum _{i=1}^{k}{|N_i|} \ge k\cdot \delta n\ge \delta ^2 n^2\ge D n\log n,\end{equation*}
where in the last step we used our assumption that
![]() $n \ge N \ge n_2$
.
$n \ge N \ge n_2$
.
We can now use that
![]() $G$
satisfies property
$G$
satisfies property
![]() $\textsf{P}(H,\delta,\lceil Dn\log n\rceil )$
, which directly implies that there exists a pair
$\textsf{P}(H,\delta,\lceil Dn\log n\rceil )$
, which directly implies that there exists a pair
![]() $(i,j) \in [k]^2$
such that
$(i,j) \in [k]^2$
such that
![]() $x_iy_j \in E(H)$
and
$x_iy_j \in E(H)$
and
![]() $G$
contains all edges of the form
$G$
contains all edges of the form
![]() $xy$
where
$xy$
where
![]() $(x,y) \in Z_{x_i}\times Z_{y_j}$
. However, by definition of
$(x,y) \in Z_{x_i}\times Z_{y_j}$
. However, by definition of
![]() $F$
this means that there exists no edge in
$F$
this means that there exists no edge in
![]() $F$
which has endpoints in both
$F$
which has endpoints in both
![]() $Z_{x_i}$
and
$Z_{x_i}$
and
![]() $Z_{y_j}$
. This is a contradiction to our initial assumption that
$Z_{y_j}$
. This is a contradiction to our initial assumption that
![]() $(Z_h)_{h \in V(H)}$
form an
$(Z_h)_{h \in V(H)}$
form an
![]() $H$
-minor model in
$H$
-minor model in
![]() $F$
. Thus,
$F$
. Thus,
![]() $F$
does not contain
$F$
does not contain
![]() $H$
as a minor, which establishes the third item of the lemma and concludes the proof.
$H$
as a minor, which establishes the third item of the lemma and concludes the proof.
Our next lemma below guarantees that for sufficiently well-connected graphs
![]() $H$
, the property of being
$H$
, the property of being
![]() $H$
-minor-free is preserved when pasting together two graphs along a sufficiently small clique. This statement will then be used in the proof of Theorem 5 to glue several copies of the
$H$
-minor-free is preserved when pasting together two graphs along a sufficiently small clique. This statement will then be used in the proof of Theorem 5 to glue several copies of the
![]() $H$
-minor-free graph from Lemma 12 along a common clique, thus eventually creating a graph that is still
$H$
-minor-free graph from Lemma 12 along a common clique, thus eventually creating a graph that is still
![]() $H$
-minor-free but has an increased list chromatic number. The lemma is folklore in the graph minors community, see also Section 3.1 in [Reference Norin19].
$H$
-minor-free but has an increased list chromatic number. The lemma is folklore in the graph minors community, see also Section 3.1 in [Reference Norin19].
Lemma 13.
Let
![]() $G_1, G_2$
be
$G_1, G_2$
be
![]() $H$
-minor-free graphs and let
$H$
-minor-free graphs and let
![]() $C\;:\!=\;V(G_1) \cap V(G_2)$
. If
$C\;:\!=\;V(G_1) \cap V(G_2)$
. If
![]() $C$
forms a clique in both
$C$
forms a clique in both
![]() $G_1$
and
$G_1$
and
![]() $G_2$
and if
$G_2$
and if
![]() $|C|\lt \kappa (H)$
, then the graph union
$|C|\lt \kappa (H)$
, then the graph union
![]() $G_1 \cup G_2$
is also
$G_1 \cup G_2$
is also
![]() $H$
-minor-free.
$H$
-minor-free.
The last ingredient required to complete the proof of Theorem 5 is a simple but important idea on how to lower-bound the list chromatic number of a graph that is obtained from a fixed graph
![]() $F$
by repeated pasting along the same clique. Since the statement will also be reused for the proof of Theorem 7 in the next section, we decided to isolate it here. We use the following terminology:
$F$
by repeated pasting along the same clique. Since the statement will also be reused for the proof of Theorem 7 in the next section, we decided to isolate it here. We use the following terminology:
Definition 14 (Pasting). Let
![]() $F$
be a graph, let
$F$
be a graph, let
![]() $S \subseteq V(F)$
and
$S \subseteq V(F)$
and
![]() $K \in \mathbb{N}$
. A
$K \in \mathbb{N}$
. A
![]() $K$
-fold pasting of
$K$
-fold pasting of
![]() $F$
at
$F$
at
![]() $S$
is any graph that can be expressed as the union of
$S$
is any graph that can be expressed as the union of
![]() $K$
isomorphic copies
$K$
isomorphic copies
![]() $F_1, \ldots,F_K$
of
$F_1, \ldots,F_K$
of
![]() $F$
with the property that
$F$
with the property that
![]() $V(F_i) \cap V(F_j)=S$
for all
$V(F_i) \cap V(F_j)=S$
for all
![]() $1 \le i \lt j \le K$
.
$1 \le i \lt j \le K$
.
Lemma 15.
Let
![]() $m,n,d \in \mathbb{N}$
with
$m,n,d \in \mathbb{N}$
with
![]() $d \le m$
and let
$d \le m$
and let
![]() $F$
be a graph whose vertex set is partitioned into two cliques
$F$
be a graph whose vertex set is partitioned into two cliques
![]() $A$
,
$A$
,
![]() $B$
such that every vertex in
$B$
such that every vertex in
![]() $B$
has at least
$B$
has at least
![]() $|A|-d$
neighbours in
$|A|-d$
neighbours in
![]() $A$
. Let
$A$
. Let
![]() $K = (|A|+|B|-1)^{|A|}$
and let
$K = (|A|+|B|-1)^{|A|}$
and let
![]() $F^{(K)}$
be a
$F^{(K)}$
be a
![]() $K$
-fold pasting of
$K$
-fold pasting of
![]() $F$
at
$F$
at
![]() $A$
. Then
$A$
. Then
![]() $\chi _\ell (F^{(K)}) \geq |A|+|B|-d$
.
$\chi _\ell (F^{(K)}) \geq |A|+|B|-d$
.
Proof. Let
![]() $F_1,\ldots,F_K$
be an ordering of the copies of
$F_1,\ldots,F_K$
be an ordering of the copies of
![]() $F$
in the pasting graph
$F$
in the pasting graph
![]() $F^{(K)}$
, and let
$F^{(K)}$
, and let
![]() $B_1,\ldots,B_K$
be the corresponding copies of
$B_1,\ldots,B_K$
be the corresponding copies of
![]() $B$
. Let
$B$
. Let
![]() $f : [|A|+|B|-1]^A \rightarrow [K]$
be an arbitrary bijection and let
$f : [|A|+|B|-1]^A \rightarrow [K]$
be an arbitrary bijection and let
![]() $c_1,\ldots,c_K : A \rightarrow [|A|+|B|-1]$
be the ordering of colour assignments to
$c_1,\ldots,c_K : A \rightarrow [|A|+|B|-1]$
be the ordering of colour assignments to
![]() $A$
that satisfies
$A$
that satisfies
![]() $f(c_i) = i$
for all
$f(c_i) = i$
for all
![]() $i \in [K]$
. Consider the list assignment
$i \in [K]$
. Consider the list assignment
![]() $L : V(F^{(K)}) \rightarrow 2^{[|A|+|B|-1]}$
defined as follows:
$L : V(F^{(K)}) \rightarrow 2^{[|A|+|B|-1]}$
defined as follows:
 $L(a) \;:\!=\; [|A|+|B|-1]$
for all
$L(a) \;:\!=\; [|A|+|B|-1]$
for all
 $a \in A$
$a \in A$
 $L(b) \;:\!=\; [|A|+|B|-1] \setminus \{c_i(a) \mid a \in A \setminus N_{F_i}(b) \}$
for all
$L(b) \;:\!=\; [|A|+|B|-1] \setminus \{c_i(a) \mid a \in A \setminus N_{F_i}(b) \}$
for all
 $b \in B_i$
for all
$b \in B_i$
for all
 $i \in [K]$
$i \in [K]$
Given that every vertex in
![]() $B$
by assumption has at most
$B$
by assumption has at most
![]() $d$
non-neighbors in
$d$
non-neighbors in
![]() $F$
, we have
$F$
, we have
![]() $|L(v)| \geq |A|+|B|-1-d$
for all
$|L(v)| \geq |A|+|B|-1-d$
for all
![]() $v \in V(F^{(K)})$
. Now assume towards a contradiction that
$v \in V(F^{(K)})$
. Now assume towards a contradiction that
![]() $F^{(K)}$
admits a proper
$F^{(K)}$
admits a proper
![]() $L$
-colouring
$L$
-colouring
![]() $c$
and let
$c$
and let
![]() $i \in [K]$
be the unique index satisfying
$i \in [K]$
be the unique index satisfying
![]() $c_i(a) = c(a)$
for all
$c_i(a) = c(a)$
for all
![]() $a \in A$
. Then let
$a \in A$
. Then let
![]() $c_{F_i} : A \cup B_i \rightarrow [|A|+|B|-1]$
be the colouring
$c_{F_i} : A \cup B_i \rightarrow [|A|+|B|-1]$
be the colouring
![]() $c$
restricted to the graph
$c$
restricted to the graph
![]() $F_i$
. Since
$F_i$
. Since
![]() ${\textrm{v}}(F_i) = |A|+|B|$
, there exist by the pigeonhole principle vertices
${\textrm{v}}(F_i) = |A|+|B|$
, there exist by the pigeonhole principle vertices
![]() $u,v \in V(F_i)$
with
$u,v \in V(F_i)$
with
![]() $c(u) = c(v)$
. Since
$c(u) = c(v)$
. Since
![]() $c$
is proper and
$c$
is proper and
![]() $A$
,
$A$
,
![]() $B$
are cliques, we have
$B$
are cliques, we have
![]() $uv \notin E(F_i)$
and
$uv \notin E(F_i)$
and
![]() $u \in A$
,
$u \in A$
,
![]() $v \in B$
without loss of generality. However,
$v \in B$
without loss of generality. However,
![]() $c(u) \notin L(v)$
by the construction of
$c(u) \notin L(v)$
by the construction of
![]() $L$
, a contradiction.
$L$
, a contradiction.
By assembling the previously established pieces, we can now easily deduce Theorem 5.
Proof of Theorem
5. Let a constant
![]() $\varepsilon \gt 0$
be given choose
$\varepsilon \gt 0$
be given choose
![]() $\tilde{\varepsilon }\in (0, \frac{\varepsilon }{4})$
. Let
$\tilde{\varepsilon }\in (0, \frac{\varepsilon }{4})$
. Let
![]() $N=N(\tilde{\varepsilon })$
be as in Lemma 12. We now set
$N=N(\tilde{\varepsilon })$
be as in Lemma 12. We now set
![]() $n_0\;:\!=\;\max \{N,\lceil \frac{4}{\varepsilon ^2}\rceil \rceil \}$
and claim that Theorem 5 holds for this choice of
$n_0\;:\!=\;\max \{N,\lceil \frac{4}{\varepsilon ^2}\rceil \rceil \}$
and claim that Theorem 5 holds for this choice of
![]() $n_0$
.
$n_0$
.
Let
![]() $H$
be a graph on
$H$
be a graph on
![]() $n \ge n_0$
vertices. We have to prove that
$n \ge n_0$
vertices. We have to prove that
![]() $f_\ell (H)\ge (1-\varepsilon )(n+\kappa (H))$
. If
$f_\ell (H)\ge (1-\varepsilon )(n+\kappa (H))$
. If
![]() $\kappa (H)\lt \varepsilon n$
, then this follows directly from the trivial lower bound via
$\kappa (H)\lt \varepsilon n$
, then this follows directly from the trivial lower bound via
Thus, we may now assume
![]() $\kappa (H)\ge \varepsilon n$
, in particular,
$\kappa (H)\ge \varepsilon n$
, in particular,
![]() $\kappa (H) \ge \tilde{\varepsilon } n$
. Using
$\kappa (H) \ge \tilde{\varepsilon } n$
. Using
![]() $n \ge N$
and Lemma 12 we now find that there exists an
$n \ge N$
and Lemma 12 we now find that there exists an
![]() $H$
-minor-free graph
$H$
-minor-free graph
![]() $F$
whose vertex set is partitioned into two cliques
$F$
whose vertex set is partitioned into two cliques
![]() $A, B$
such that
$A, B$
such that
![]() $|A|=\lfloor (1-2\tilde{\varepsilon })\kappa (H)\rfloor \lt \kappa (H)$
and
$|A|=\lfloor (1-2\tilde{\varepsilon })\kappa (H)\rfloor \lt \kappa (H)$
and
![]() $|B|=\lfloor (1-2\tilde{\varepsilon })n\rfloor$
, and such that every vertex in
$|B|=\lfloor (1-2\tilde{\varepsilon })n\rfloor$
, and such that every vertex in
![]() $B$
has at most
$B$
has at most
![]() $\tilde{\varepsilon }n$
non-neighbors in
$\tilde{\varepsilon }n$
non-neighbors in
![]() $F$
. Let
$F$
. Let
![]() $d\;:\!=\;\lfloor \tilde{\varepsilon }n \rfloor$
and
$d\;:\!=\;\lfloor \tilde{\varepsilon }n \rfloor$
and
![]() $K\;:\!=\;(|A|+|B|-1)^{|A|}$
. Let
$K\;:\!=\;(|A|+|B|-1)^{|A|}$
. Let
![]() $F^{(K)}$
denote a
$F^{(K)}$
denote a
![]() $K$
-fold pasting of
$K$
-fold pasting of
![]() $F$
at the clique
$F$
at the clique
![]() $A$
. Since every vertex in
$A$
. Since every vertex in
![]() $B$
has at least
$B$
has at least
![]() $|A|-d$
neighbours in
$|A|-d$
neighbours in
![]() $A$
, we can apply Lemma 15 to find that
$A$
, we can apply Lemma 15 to find that
using
![]() $n \ge n_0 \ge \frac{4}{\varepsilon ^2}$
in the last step. In addition, since
$n \ge n_0 \ge \frac{4}{\varepsilon ^2}$
in the last step. In addition, since
![]() $|A|\lt \kappa (H)$
, the graph
$|A|\lt \kappa (H)$
, the graph
![]() $F^{(K)}$
is
$F^{(K)}$
is
![]() $H$
-minor-free by repeated application of Lemma 13. We conclude that
$H$
-minor-free by repeated application of Lemma 13. We conclude that
![]() $f_\ell (H)\ge (1-\varepsilon )({\textrm{v}}(H)+\kappa (H))$
, as desired.
$f_\ell (H)\ge (1-\varepsilon )({\textrm{v}}(H)+\kappa (H))$
, as desired.
4. Proof of Theorem 7
In this section, we present the proof of Theorem 7. The theorem claims a lower bound on
![]() $f_\ell (H)$
for almost all graphs
$f_\ell (H)$
for almost all graphs
![]() $H$
on
$H$
on
![]() $n$
vertices and
$n$
vertices and
![]() $\lceil C n \log n\rceil$
edges for some large constant
$\lceil C n \log n\rceil$
edges for some large constant
![]() $C\gt 0$
. However, in fact the only condition on the graph
$C\gt 0$
. However, in fact the only condition on the graph
![]() $H$
our lower bound proof relies upon is the following pseudo-random graph property, guaranteeing the existence of many edges between every pair of disjoint linear-size vertex subsets in
$H$
our lower bound proof relies upon is the following pseudo-random graph property, guaranteeing the existence of many edges between every pair of disjoint linear-size vertex subsets in
![]() $H$
.
$H$
.
Definition 16 (Property
![]() $\textsf{Q}$
, graph family
$\textsf{Q}$
, graph family
![]() $\mathcal{Q}_n$
). Let
$\mathcal{Q}_n$
). Let
![]() $\delta \gt 0$
and
$\delta \gt 0$
and
![]() $D \gt 1$
be arbitrary. We say that a graph
$D \gt 1$
be arbitrary. We say that a graph
![]() $H$
with
$H$
with
![]() $n$
vertices satisfies property
$n$
vertices satisfies property
![]() $\textsf{Q}(\delta, D)$
if for every two disjoint vertex sets
$\textsf{Q}(\delta, D)$
if for every two disjoint vertex sets
![]() $A, B \subseteq V(H)$
with
$A, B \subseteq V(H)$
with
![]() $|A|,|B| \geq \delta n$
, we have
$|A|,|B| \geq \delta n$
, we have
![]() ${\textrm{e}}_H(A,B)\ge D n \log n$
. Let
${\textrm{e}}_H(A,B)\ge D n \log n$
. Let
![]() $\mathcal{Q}_{n} (\delta, D)$
denote the family of
$\mathcal{Q}_{n} (\delta, D)$
denote the family of
![]() $n$
-vertex graphs
$n$
-vertex graphs
![]() $H$
that satisfy property
$H$
that satisfy property
![]() $\textsf{Q}(\delta, D)$
.
$\textsf{Q}(\delta, D)$
.
Crucially, property
![]() $\textsf{Q}(\delta,D)$
is satisfied for almost all graphs on
$\textsf{Q}(\delta,D)$
is satisfied for almost all graphs on
![]() $n$
vertices with an average degree of
$n$
vertices with an average degree of
![]() $C\log n$
for a large enough constant
$C\log n$
for a large enough constant
![]() $C$
. The proof uses a standard probabilistic argument and is therefore omitted.
$C$
. The proof uses a standard probabilistic argument and is therefore omitted.
Lemma 17.
Let
![]() $\delta \gt 0$
,
$\delta \gt 0$
,
![]() $D \gt 1$
be arbitrary and let
$D \gt 1$
be arbitrary and let
![]() $m:\mathbb{N}\rightarrow \mathbb{N}$
be defined as
$m:\mathbb{N}\rightarrow \mathbb{N}$
be defined as
![]() $m(n) = \lceil \frac{D^2}{ \delta ^2} n\log n\rceil$
. Then with high probability as
$m(n) = \lceil \frac{D^2}{ \delta ^2} n\log n\rceil$
. Then with high probability as
![]() $n \rightarrow \infty$
, a random graph
$n \rightarrow \infty$
, a random graph
![]() $H = G(n;m(n))$
drawn uniformly from all
$H = G(n;m(n))$
drawn uniformly from all
![]() $n$
-vertex graphs with
$n$
-vertex graphs with
![]() $m(n)$
edges satisfies property
$m(n)$
edges satisfies property
![]() $\textsf{Q}(\delta, D)$
.
$\textsf{Q}(\delta, D)$
.
In our next step towards proving Theorem 7, we establish the following statement somewhat analogous to Lemma 12, showing how to build small and close-to-complete
![]() $H$
-minor-free graphs for a given graph
$H$
-minor-free graphs for a given graph
![]() $H \in \mathcal{Q}_n(\delta,D)$
.
$H \in \mathcal{Q}_n(\delta,D)$
.
Lemma 18.
Let
![]() $\delta \in (0,1)$
,
$\delta \in (0,1)$
,
![]() $D \gt 1$
,
$D \gt 1$
,
![]() $n \in \mathbb N$
, and
$n \in \mathbb N$
, and
![]() $H \in \mathcal{Q}_{n}(\delta, D)$
be arbitrary. Moreover, let
$H \in \mathcal{Q}_{n}(\delta, D)$
be arbitrary. Moreover, let
![]() $G$
be a bipartite graph with bipartition
$G$
be a bipartite graph with bipartition
![]() $\{A, B\}$
,
$\{A, B\}$
,
![]() $|A| = |B| = \lfloor (1-3\delta )n\rfloor$
satisfying property
$|A| = |B| = \lfloor (1-3\delta )n\rfloor$
satisfying property
![]() $\textsf{P}(H, \delta,s)$
for
$\textsf{P}(H, \delta,s)$
for
![]() $s=\lceil Dn\log n\rceil$
. Then its complement graph
$s=\lceil Dn\log n\rceil$
. Then its complement graph
![]() $G^\complement$
does not contain
$G^\complement$
does not contain
![]() $H[U]$
as a minor for any
$H[U]$
as a minor for any
![]() $U \subseteq V(H)$
with
$U \subseteq V(H)$
with
![]() $|U| \geq (1-\delta )n$
.
$|U| \geq (1-\delta )n$
.
Proof. Assume
![]() $G^\complement$
contains
$G^\complement$
contains
![]() $H[U]$
as a minor for some
$H[U]$
as a minor for some
![]() $U \subseteq V(H)$
with
$U \subseteq V(H)$
with
![]() $|U| \geq (1-\delta )n$
. Let
$|U| \geq (1-\delta )n$
. Let
![]() $(Z_h)_{h \in U}$
be an
$(Z_h)_{h \in U}$
be an
![]() $H[U]$
-minor model in
$H[U]$
-minor model in
![]() $G^\complement$
and define
$G^\complement$
and define
![]() $X_A \;:\!=\; \{h \in U \mid Z_h \subseteq A\}$
,
$X_A \;:\!=\; \{h \in U \mid Z_h \subseteq A\}$
,
![]() $X_B \;:\!=\; \{h \in U \mid Z_h \subseteq B\}$
, and
$X_B \;:\!=\; \{h \in U \mid Z_h \subseteq B\}$
, and
![]() $X_{AB} \;:\!=\; \{h \in U \mid Z_h \cap A \neq \emptyset \neq \ Z_h \cap B\}$
. We have
$X_{AB} \;:\!=\; \{h \in U \mid Z_h \cap A \neq \emptyset \neq \ Z_h \cap B\}$
. We have
![]() $|X_A| + |X_{AB}| \leq |A|$
,
$|X_A| + |X_{AB}| \leq |A|$
,
![]() $|X_B| + |X_{AB}| \leq |B|$
, and
$|X_B| + |X_{AB}| \leq |B|$
, and
![]() $|X_A| + |X_B| + |X_{AB}|=|U| \geq (1-\delta )n$
, which implies
$|X_A| + |X_B| + |X_{AB}|=|U| \geq (1-\delta )n$
, which implies
![]() $|X_A|, |X_B| \ge (1-\delta )n-(1-3\delta )n=2\delta n$
.
$|X_A|, |X_B| \ge (1-\delta )n-(1-3\delta )n=2\delta n$
.
Since the branch sets
![]() $(Z_h)_{h \in X_A}$
in
$(Z_h)_{h \in X_A}$
in
![]() $A$
and the branch-sets
$A$
and the branch-sets
![]() $(Z_h)_{h \in X_B}$
in
$(Z_h)_{h \in X_B}$
in
![]() $B$
are pairwise disjoint, at most
$B$
are pairwise disjoint, at most
![]() $\delta (1-3\delta ) n\lt \delta n$
branch sets in each of
$\delta (1-3\delta ) n\lt \delta n$
branch sets in each of
![]() $(Z_h)_{h \in X_A}$
and
$(Z_h)_{h \in X_A}$
and
![]() $(Z_h)_{h \in X_B}$
can be larger than
$(Z_h)_{h \in X_B}$
can be larger than
![]() $\frac{1}{\delta }$
. Thus, there are at least
$\frac{1}{\delta }$
. Thus, there are at least
![]() $2\delta n-\delta n=\delta n$
branch sets of size at most
$2\delta n-\delta n=\delta n$
branch sets of size at most
![]() $\frac{1}{\delta }$
in
$\frac{1}{\delta }$
in
![]() $(Z_h)_{h \in X_A}$
as well as in
$(Z_h)_{h \in X_A}$
as well as in
![]() $(Z_h)_{h \in X_B}$
. Thus for
$(Z_h)_{h \in X_B}$
. Thus for
![]() $k\;:\!=\;l\;:\!=\; \lceil \delta n \rceil$
, there exist distinct vertices
$k\;:\!=\;l\;:\!=\; \lceil \delta n \rceil$
, there exist distinct vertices
![]() $x_1, \ldots, x_{k} \in X_A$
,
$x_1, \ldots, x_{k} \in X_A$
,
![]() $y_1,\ldots,y_l \in X_B$
such that
$y_1,\ldots,y_l \in X_B$
such that
![]() $|Z_{x_i}|, |Z_{y_j}| \le \frac{1}{\delta }$
for all
$|Z_{x_i}|, |Z_{y_j}| \le \frac{1}{\delta }$
for all
![]() $1 \le i, j \le k=l$
. Since
$1 \le i, j \le k=l$
. Since
![]() $H\in \mathcal{Q}_n(\delta,D)$
, we have
$H\in \mathcal{Q}_n(\delta,D)$
, we have
![]() ${\textrm{e}}_H(\{x_1,\ldots,x_k\},\{y_1,\ldots,y_l\})\ge \lceil D n \log n\rceil =s$
. Next we use our assumption that
${\textrm{e}}_H(\{x_1,\ldots,x_k\},\{y_1,\ldots,y_l\})\ge \lceil D n \log n\rceil =s$
. Next we use our assumption that
![]() $G$
satisfies property
$G$
satisfies property
![]() $\textsf{P}(H, \delta,s)$
. It implies that there exists an edge
$\textsf{P}(H, \delta,s)$
. It implies that there exists an edge
![]() $x_i y_j \in E(H)$
with
$x_i y_j \in E(H)$
with
![]() $(i,j) \in [k]\times [l]$
such that
$(i,j) \in [k]\times [l]$
such that
![]() $G$
contains all the edges
$G$
contains all the edges
![]() $xy$
with
$xy$
with
![]() $(x,y) \in Z_{x_i} \times Z_{y_j}$
. Then, however, there is an edge between vertices
$(x,y) \in Z_{x_i} \times Z_{y_j}$
. Then, however, there is an edge between vertices
![]() $x_i$
and
$x_i$
and
![]() $y_j$
in
$y_j$
in
![]() $H$
, but no edge between the corresponding branch sets
$H$
, but no edge between the corresponding branch sets
![]() $Z_{x_i}$
and
$Z_{x_i}$
and
![]() $Z_{y_j}$
in
$Z_{y_j}$
in
![]() $G^\complement$
, a contradiction.
$G^\complement$
, a contradiction.
The next auxiliary statement we need is Lemma 19 below, which establishes a weak analogue of Lemma 13 for graphs
![]() $H\in \mathcal{Q}_n(\delta,D)$
. Note that as these graphs may have sublinear minimum degree and connectivity, Lemma 13 cannot be used to obtain the same statement.
$H\in \mathcal{Q}_n(\delta,D)$
. Note that as these graphs may have sublinear minimum degree and connectivity, Lemma 13 cannot be used to obtain the same statement.
Lemma 19.
Let
![]() $\delta \gt 0$
,
$\delta \gt 0$
,
![]() $D \gt 1$
,
$D \gt 1$
,
![]() $H \in \mathcal{Q}_n(\delta, D)$
and let
$H \in \mathcal{Q}_n(\delta, D)$
and let
![]() $F$
be a graph with a clique
$F$
be a graph with a clique
![]() $W \subseteq V(F)$
of size
$W \subseteq V(F)$
of size
![]() $\lfloor (1-3\delta )n\rfloor$
. Let
$\lfloor (1-3\delta )n\rfloor$
. Let
![]() $K \in \mathbb{N}$
and let
$K \in \mathbb{N}$
and let
![]() $F^{(K)}$
be a
$F^{(K)}$
be a
![]() $K$
-fold pasting of
$K$
-fold pasting of
![]() $F$
at
$F$
at
![]() $W$
. If
$W$
. If
![]() $F^{(K)}$
contains
$F^{(K)}$
contains
![]() $H$
as a minor, then there exists
$H$
as a minor, then there exists
![]() $U \subseteq V(H)$
with
$U \subseteq V(H)$
with
![]() $|U|\ge (1-\delta )n$
such that
$|U|\ge (1-\delta )n$
such that
![]() $F$
contains
$F$
contains
![]() $H[U]$
as a minor.
$H[U]$
as a minor.
Proof. In the following, let
![]() $F_1, \ldots, F_K$
denote the copies of
$F_1, \ldots, F_K$
denote the copies of
![]() $F$
such that
$F$
such that
![]() $F^{(K)}=\bigcup _{i=1}^{K}{F_i}$
.
$F^{(K)}=\bigcup _{i=1}^{K}{F_i}$
.
Suppose
![]() $F^{(K)}$
has an
$F^{(K)}$
has an
![]() $H$
-minor and fix an
$H$
-minor and fix an
![]() $H$
-minor model
$H$
-minor model
![]() $(Z_h)_{h\in V(H)}$
in
$(Z_h)_{h\in V(H)}$
in
![]() $H$
. Let us denote
$H$
. Let us denote
![]() $X_W \;:\!=\; \{h \in V(H) \mid Z_h \cap W \neq \emptyset \}$
and
$X_W \;:\!=\; \{h \in V(H) \mid Z_h \cap W \neq \emptyset \}$
and
![]() $\xi _W\;:\!=\;|X_W|$
, and
$\xi _W\;:\!=\;|X_W|$
, and
![]() $X_i \;:\!=\; \{h \in V(H) \mid Z_h \subseteq V(F_i) \setminus W\}$
and
$X_i \;:\!=\; \{h \in V(H) \mid Z_h \subseteq V(F_i) \setminus W\}$
and
![]() $\xi _i\;:\!=\;|X_i|$
for every
$\xi _i\;:\!=\;|X_i|$
for every
![]() $i \in [K]$
. Note that since every branch-set
$i \in [K]$
. Note that since every branch-set
![]() $Z_h$
induces a connected subgraph of
$Z_h$
induces a connected subgraph of
![]() $F$
, every vertex
$F$
, every vertex
![]() $h \in V(H)$
appears in exactly one of the sets
$h \in V(H)$
appears in exactly one of the sets
![]() $X_W, X_1,\ldots,X_K$
, i.e., they form a partition of
$X_W, X_1,\ldots,X_K$
, i.e., they form a partition of
![]() $V(H)$
. In particular, we have
$V(H)$
. In particular, we have
![]() $\xi _W+\sum _{i=1}^{K}{\xi _i}={\textrm{v}}(H)=n$
.
$\xi _W+\sum _{i=1}^{K}{\xi _i}={\textrm{v}}(H)=n$
.
We have
![]() $\xi _W \leq |W|\le n-3\delta n$
and thus
$\xi _W \leq |W|\le n-3\delta n$
and thus
![]() $\sum _{i=1}^{K} \xi _i=n-\xi _W \geq 3 \delta n$
. In the following, let us w.l.o.g. assume
$\sum _{i=1}^{K} \xi _i=n-\xi _W \geq 3 \delta n$
. In the following, let us w.l.o.g. assume
![]() $[K]$
is ordered such that
$[K]$
is ordered such that
![]() $\xi _1 \geq \xi _2 \geq \cdots \geq \xi _K$
. We claim that
$\xi _1 \geq \xi _2 \geq \cdots \geq \xi _K$
. We claim that
![]() $\xi _1\ge (1-\delta )n-\xi _W$
. Towards a contradiction, suppose in the following that
$\xi _1\ge (1-\delta )n-\xi _W$
. Towards a contradiction, suppose in the following that
![]() $\xi _1 \lt (1-\delta )n - \xi _W$
. We first note that using this assumption, we have that
$\xi _1 \lt (1-\delta )n - \xi _W$
. We first note that using this assumption, we have that
![]() $\sum _{i=2}^K \xi _i=n-(\xi _W+\xi _1) \gt n-(1-\delta )n=\delta n$
.
$\sum _{i=2}^K \xi _i=n-(\xi _W+\xi _1) \gt n-(1-\delta )n=\delta n$
.
Now suppose for a first case that
![]() $\xi _1 \ge \delta n$
. Then the two disjoint sets of vertices
$\xi _1 \ge \delta n$
. Then the two disjoint sets of vertices
![]() $X_1$
and
$X_1$
and
![]() $\bigcup _{i=2}^{K}{X_i}$
in
$\bigcup _{i=2}^{K}{X_i}$
in
![]() $H$
are both of size at least
$H$
are both of size at least
![]() $\delta n$
. By property
$\delta n$
. By property
![]() $\textsf{Q}(\delta,D)$
this implies that
$\textsf{Q}(\delta,D)$
this implies that
![]() ${\textrm{e}}_H(X_1,\bigcup _{i=2}^{K}{X_i})\ge Dn\log n\gt 0$
. In particular there exists
${\textrm{e}}_H(X_1,\bigcup _{i=2}^{K}{X_i})\ge Dn\log n\gt 0$
. In particular there exists
![]() $2 \le i \le K$
and an edge
$2 \le i \le K$
and an edge
![]() $uv\in E(H)$
for some
$uv\in E(H)$
for some
![]() $u \in X_1$
and
$u \in X_1$
and
![]() $v \in X_i$
. This implies that there must exist an edge in
$v \in X_i$
. This implies that there must exist an edge in
![]() $F^{(K)}$
connecting a vertex in
$F^{(K)}$
connecting a vertex in
![]() $Z_u\subseteq V(F_1)\setminus W$
to a vertex in
$Z_u\subseteq V(F_1)\setminus W$
to a vertex in
![]() $Z_v\subseteq V(F_i)\setminus W$
. However, by construction of
$Z_v\subseteq V(F_i)\setminus W$
. However, by construction of
![]() $F^{(K)}$
no such edges exist, and so we arrive at the desired contradiction in this first case.
$F^{(K)}$
no such edges exist, and so we arrive at the desired contradiction in this first case.
For the second case, suppose that
![]() $\xi _1\lt \delta n$
(and thus in particular
$\xi _1\lt \delta n$
(and thus in particular
![]() $\xi _i\lt \delta n$
for all
$\xi _i\lt \delta n$
for all
![]() $i \in [K]$
). Let
$i \in [K]$
). Let
![]() $j \in [K]$
be the smallest index such that
$j \in [K]$
be the smallest index such that
![]() $\sum _{i=1}^{j}{\xi _i}\gt \delta n$
(this is well-defined, since
$\sum _{i=1}^{j}{\xi _i}\gt \delta n$
(this is well-defined, since
![]() $\sum _{i=1}^K{\xi _i}\ge 3\delta n$
, see above). By the minimality of
$\sum _{i=1}^K{\xi _i}\ge 3\delta n$
, see above). By the minimality of
![]() $j$
, we have
$j$
, we have
![]() $\sum _{i=1}^{j}{\xi _i}=\xi _j+\sum _{i=1}^{j-1}{\xi _j}\le \delta n+\delta n=2\delta n$
. This implies that
$\sum _{i=1}^{j}{\xi _i}=\xi _j+\sum _{i=1}^{j-1}{\xi _j}\le \delta n+\delta n=2\delta n$
. This implies that
![]() $\sum _{i=j+1}^K{\xi _i}=\sum _{i=1}^K{\xi _i}-\sum _{i=1}^j{\xi _i}\ge 3\delta n - 2\delta n =\delta n$
. In consequence, we find that the two disjoint vertex sets
$\sum _{i=j+1}^K{\xi _i}=\sum _{i=1}^K{\xi _i}-\sum _{i=1}^j{\xi _i}\ge 3\delta n - 2\delta n =\delta n$
. In consequence, we find that the two disjoint vertex sets
![]() $\bigcup _{i=1}^{j}{X_i}, \bigcup _{i=j+1}^{K}{X_i}$
in
$\bigcup _{i=1}^{j}{X_i}, \bigcup _{i=j+1}^{K}{X_i}$
in
![]() $H$
are both of size at least
$H$
are both of size at least
![]() $\delta n$
. Hence, using property
$\delta n$
. Hence, using property
![]() $\textsf{Q}(\delta,D)$
we have
$\textsf{Q}(\delta,D)$
we have
![]() ${\textrm{e}}_H(\bigcup _{i=1}^{j}{X_i},\bigcup _{i=j+1}^{K}{X_i})\ge Dn\log n\gt 0$
. Similar as above, this implies the existence of two indices
${\textrm{e}}_H(\bigcup _{i=1}^{j}{X_i},\bigcup _{i=j+1}^{K}{X_i})\ge Dn\log n\gt 0$
. Similar as above, this implies the existence of two indices
![]() $i,i'$
with
$i,i'$
with
![]() $1 \le i\le j\lt i'\le K$
such that there exists an edge between
$1 \le i\le j\lt i'\le K$
such that there exists an edge between
![]() $V(F_i)\setminus W$
and
$V(F_i)\setminus W$
and
![]() $V(F_{i'})\setminus W$
in
$V(F_{i'})\setminus W$
in
![]() $F^{(K)}$
. As this is impossible by construction of
$F^{(K)}$
. As this is impossible by construction of
![]() $F^{(K)}$
, a contradiction follows also in the second case. Thus our initial assumption
$F^{(K)}$
, a contradiction follows also in the second case. Thus our initial assumption
![]() $\xi _1\lt (1-\delta )n-\xi _W$
was false.
$\xi _1\lt (1-\delta )n-\xi _W$
was false.
We therefore have
![]() $|X_1 \cup X_W|=\xi _1+\xi _W \geq (1-\delta )n$
. Let
$|X_1 \cup X_W|=\xi _1+\xi _W \geq (1-\delta )n$
. Let
![]() $U\;:\!=\;X_1 \cup X_W$
. For every
$U\;:\!=\;X_1 \cup X_W$
. For every
![]() $h \in U$
, let
$h \in U$
, let
![]() $Z_h'\;:\!=\;Z_h$
if
$Z_h'\;:\!=\;Z_h$
if
![]() $h \in X_1$
and
$h \in X_1$
and
![]() $Z_h'\;:\!=\;Z_h \cap V(F_1)$
if
$Z_h'\;:\!=\;Z_h \cap V(F_1)$
if
![]() $h \in X_W$
. We now show that
$h \in X_W$
. We now show that
![]() $(Z_h')_{h \in U}$
is an
$(Z_h')_{h \in U}$
is an
![]() $H[U]$
-minor model in
$H[U]$
-minor model in
![]() $F_1$
, which will then conclude the proof of the lemma.
$F_1$
, which will then conclude the proof of the lemma.
First of all, note that
![]() $F_1[Z_h']$
is a connected graph for every
$F_1[Z_h']$
is a connected graph for every
![]() $h \in U$
. If
$h \in U$
. If
![]() $h \in X_1$
, then
$h \in X_1$
, then
![]() $F_1[Z_h']=F^{(K)}[Z_h]$
is connected since
$F_1[Z_h']=F^{(K)}[Z_h]$
is connected since
![]() $(Z_h)_{h \in V(H)}$
is an
$(Z_h)_{h \in V(H)}$
is an
![]() $H$
-minor model. And if
$H$
-minor model. And if
![]() $h \in X_W$
, then the connectivity of
$h \in X_W$
, then the connectivity of
![]() $F_1[Z_h']=F^{(k)}[Z_h \cap V(F_1)]$
follows since (1)
$F_1[Z_h']=F^{(k)}[Z_h \cap V(F_1)]$
follows since (1)
![]() $F^{(K)}[Z_h]$
is connected and (2) every path connecting two vertices in
$F^{(K)}[Z_h]$
is connected and (2) every path connecting two vertices in
![]() $Z_h'$
that is contained in
$Z_h'$
that is contained in
![]() $F^{(K)}[Z_h]$
can be shortened to a path whose vertex set is completely contained in
$F^{(K)}[Z_h]$
can be shortened to a path whose vertex set is completely contained in
![]() $V(F_1)$
by short-cutting every segment of the path that starts and ends in the clique
$V(F_1)$
by short-cutting every segment of the path that starts and ends in the clique
![]() $W$
by the direct connection between its endpoints.
$W$
by the direct connection between its endpoints.
Let us now consider any edge
![]() $uv \in E(H[U])$
. Then there must exist an edge
$uv \in E(H[U])$
. Then there must exist an edge
![]() $xy \in E(F^{(K)})$
with
$xy \in E(F^{(K)})$
with
![]() $x \in Z_u, y \in Z_v$
. If we have
$x \in Z_u, y \in Z_v$
. If we have
![]() $x, y\in V(F_1)$
, then this witnesses the existence of an edge between
$x, y\in V(F_1)$
, then this witnesses the existence of an edge between
![]() $Z_u'$
and
$Z_u'$
and
![]() $Z_v'$
in
$Z_v'$
in
![]() $F_1$
, as desired. If on the other hand at least one of
$F_1$
, as desired. If on the other hand at least one of
![]() $x,y$
lies outside of
$x,y$
lies outside of
![]() $V(F_1)$
, then we necessarily must have
$V(F_1)$
, then we necessarily must have
![]() $Z_u \cap W \neq \emptyset \neq Z_v \cap W$
, and thus there exists an edge in the clique induced by
$Z_u \cap W \neq \emptyset \neq Z_v \cap W$
, and thus there exists an edge in the clique induced by
![]() $W$
(and thus also in
$W$
(and thus also in
![]() $F_1$
) that connects a vertex in
$F_1$
) that connects a vertex in
![]() $Z_u'$
to a vertex in
$Z_u'$
to a vertex in
![]() $Z_v'$
. All in all, this shows that
$Z_v'$
. All in all, this shows that
![]() $F_1$
contains
$F_1$
contains
![]() $H[U]$
as a minor. Since
$H[U]$
as a minor. Since
![]() $|U| \ge (1-\delta )n$
, this concludes the proof.
$|U| \ge (1-\delta )n$
, this concludes the proof.
With the previous auxiliary results at hand, we can now deduce Theorem 7.
Proof of Theorem
7. Let a constant
![]() $\varepsilon \in (0,1)$
be given. Let
$\varepsilon \in (0,1)$
be given. Let
![]() $\delta \gt 0$
be chosen small enough such that
$\delta \gt 0$
be chosen small enough such that
![]() $7\delta \lt \varepsilon$
, set
$7\delta \lt \varepsilon$
, set
![]() $p\;:\!=\;\frac{\delta }{2}$
, let
$p\;:\!=\;\frac{\delta }{2}$
, let
![]() $D=D(\delta,p)\gt 1$
be the constant given by Lemma 11, and let
$D=D(\delta,p)\gt 1$
be the constant given by Lemma 11, and let
![]() $C \;:\!=\; \frac{D^2}{\delta ^2}$
.
$C \;:\!=\; \frac{D^2}{\delta ^2}$
.
For every
![]() $n \in \mathbb{N}$
, put
$n \in \mathbb{N}$
, put
![]() $s=s(n)=\lceil Dn\log n\rceil$
. By Lemma 17, a random graph
$s=s(n)=\lceil Dn\log n\rceil$
. By Lemma 17, a random graph
![]() $H = G(n; \lceil Cn \log n\rceil )$
chosen uniformly from all
$H = G(n; \lceil Cn \log n\rceil )$
chosen uniformly from all
![]() $n$
-vertex graphs with
$n$
-vertex graphs with
![]() $\lceil Cn\log n\rceil$
edges satisfies property
$\lceil Cn\log n\rceil$
edges satisfies property
![]() $\textsf{Q}(\delta,D)$
w.h.p. as
$\textsf{Q}(\delta,D)$
w.h.p. as
![]() $n \rightarrow \infty$
. Now assume the graph
$n \rightarrow \infty$
. Now assume the graph
![]() $H$
satisfies property
$H$
satisfies property
![]() $\textsf{Q}(\delta,D)$
. By Lemmas 9 and 11, w.h.p. as
$\textsf{Q}(\delta,D)$
. By Lemmas 9 and 11, w.h.p. as
![]() $n \rightarrow \infty$
, the random bipartite graph
$n \rightarrow \infty$
, the random bipartite graph
![]() $G = G(\lfloor (1-3\delta )n\rfloor, \lfloor (1-3\delta )n\rfloor ; p )$
has maximum degree at most
$G = G(\lfloor (1-3\delta )n\rfloor, \lfloor (1-3\delta )n\rfloor ; p )$
has maximum degree at most
![]() $2p\lfloor (1-3\delta )n\rfloor \le \delta n$
and satisfies property
$2p\lfloor (1-3\delta )n\rfloor \le \delta n$
and satisfies property
![]() $\textsf{P}(H, \delta,s)$
. Now fix
$\textsf{P}(H, \delta,s)$
. Now fix
![]() $n$
large enough and consider a graph
$n$
large enough and consider a graph
![]() $G$
with bipartition
$G$
with bipartition
![]() $\{A,B\}$
,
$\{A,B\}$
,
![]() $|A|=|B|=\lfloor (1-3\delta n)\rfloor$
satisfying these two properties. By Lemma 18,
$|A|=|B|=\lfloor (1-3\delta n)\rfloor$
satisfying these two properties. By Lemma 18,
![]() $G^\complement$
does not contain any induced subgraph
$G^\complement$
does not contain any induced subgraph
![]() $H[U]$
as a minor for any
$H[U]$
as a minor for any
![]() $U \subseteq V(H)$
with
$U \subseteq V(H)$
with
![]() $|U| \geq (1-\delta ) n$
. Let
$|U| \geq (1-\delta ) n$
. Let
![]() $K \;:\!=\; (|A|+|B|-1)^{|A|}$
and let
$K \;:\!=\; (|A|+|B|-1)^{|A|}$
and let
![]() $(G^\complement )^{(K)}$
be a
$(G^\complement )^{(K)}$
be a
![]() $K$
-fold pasting of
$K$
-fold pasting of
![]() $G^\complement$
at
$G^\complement$
at
![]() $A$
. Then by Lemma 19,
$A$
. Then by Lemma 19,
![]() $(G^\complement )^{(K)}$
does not contain
$(G^\complement )^{(K)}$
does not contain
![]() $H$
as a minor. Moreover, by Lemma 15, applied with
$H$
as a minor. Moreover, by Lemma 15, applied with
![]() $d=\lfloor \delta n\rfloor$
, we find that
$d=\lfloor \delta n\rfloor$
, we find that
![]() $(G^\complement )^{(K)}$
has list chromatic number at least
$(G^\complement )^{(K)}$
has list chromatic number at least
![]() $|A|+|B|-d\gt 2(1-3\delta )n - \delta n -2 \gt (2-\varepsilon )n$
for
$|A|+|B|-d\gt 2(1-3\delta )n - \delta n -2 \gt (2-\varepsilon )n$
for
![]() $n$
large enough. This shows that w.h.p. the random graph
$n$
large enough. This shows that w.h.p. the random graph
![]() $H=G(n;\lceil Cn \log n\rceil )$
satisfies
$H=G(n;\lceil Cn \log n\rceil )$
satisfies
![]() $f_\ell (H)\ge (2-\varepsilon )n$
, which concludes the proof.
$f_\ell (H)\ge (2-\varepsilon )n$
, which concludes the proof.
5. Proof of Theorem 3
In this section we give the proof of Theorem 3, which is self-contained and independent of the results in the previous sections. A basic tool from extremal graph theory used in the proof is Turán’s theorem, in the following form:
Theorem 20 (Turán). Let
![]() $k \in \mathbb{N}$
,
$k \in \mathbb{N}$
,
![]() $k \ge 2$
and let
$k \ge 2$
and let
![]() $G$
be a graph. If
$G$
be a graph. If
![]() ${\textrm{e}}(G)\gt (1-\frac{1}{k-1})\frac{{\textrm{v}}(G)^2}{2}$
then
${\textrm{e}}(G)\gt (1-\frac{1}{k-1})\frac{{\textrm{v}}(G)^2}{2}$
then
![]() $G$
contains a clique on
$G$
contains a clique on
![]() $k$
vertices.
$k$
vertices.
We also use the following classical result regarding the minimum degree of
![]() $K_t$
-minor-free graphs, as independently proved by Kostochka [Reference Kostochka13] and Thomason [Reference Thomason32].
$K_t$
-minor-free graphs, as independently proved by Kostochka [Reference Kostochka13] and Thomason [Reference Thomason32].
Theorem 21 ([Reference Kostochka13, Reference Thomason32]). For every integer
![]() $t \ge 1$
there exists an integer
$t \ge 1$
there exists an integer
![]() $d=d(t)=O(t \sqrt{\log t})$
such that every graph of minimum degree at least
$d=d(t)=O(t \sqrt{\log t})$
such that every graph of minimum degree at least
![]() $d$
contains
$d$
contains
![]() $K_t$
as a minor. In particular, for every graph
$K_t$
as a minor. In particular, for every graph
![]() $F$
there exists
$F$
there exists
![]() $d=d(F) \in \mathbb{N}$
such that all graphs of minimum degree at least
$d=d(F) \in \mathbb{N}$
such that all graphs of minimum degree at least
![]() $d$
contain
$d$
contain
![]() $F$
as a minor.
$F$
as a minor.
Proof of Theorem
3. We start by fixing an integer
![]() $d \in \mathbb{N}$
as guaranteed by Theorem 21, i.e. such that every graph of minimum degree at least
$d \in \mathbb{N}$
as guaranteed by Theorem 21, i.e. such that every graph of minimum degree at least
![]() $d$
contains
$d$
contains
![]() $F$
as a minor. We now define
$F$
as a minor. We now define
![]() $k_0(F)\;:\!=\;\min \{d+1,9\cdot{\textrm{v}}(F)^3\}$
. Let
$k_0(F)\;:\!=\;\min \{d+1,9\cdot{\textrm{v}}(F)^3\}$
. Let
![]() $k \ge k_0(F)$
be any given integer. Let
$k \ge k_0(F)$
be any given integer. Let
![]() $H$
denote the graph obtained from
$H$
denote the graph obtained from
![]() $F$
by adding
$F$
by adding
![]() $k$
isolated vertices. We will now show that every
$k$
isolated vertices. We will now show that every
![]() $H$
-minor-free graph is
$H$
-minor-free graph is
![]() $({\textrm{v}}(H)-2)$
-degenerate, which then easily implies
$({\textrm{v}}(H)-2)$
-degenerate, which then easily implies
![]() $f_\ell (H)={\textrm{v}}(H)-1$
.
$f_\ell (H)={\textrm{v}}(H)-1$
.
Towards a contradiction, suppose that there exists an
![]() $H$
-minor-free graph
$H$
-minor-free graph
![]() $G$
which is not
$G$
which is not
![]() $({\textrm{v}}(H)-2)$
-degenerate, and let
$({\textrm{v}}(H)-2)$
-degenerate, and let
![]() $G$
be chosen such that
$G$
be chosen such that
![]() ${\textrm{v}}(G)$
is minimised. Note that the minimality assumption on
${\textrm{v}}(G)$
is minimised. Note that the minimality assumption on
![]() $G$
immediately implies that
$G$
immediately implies that
![]() $\delta (G)\ge{\textrm{v}}(H)-1={\textrm{v}}(F)+k-1$
. Observe that since
$\delta (G)\ge{\textrm{v}}(H)-1={\textrm{v}}(F)+k-1$
. Observe that since
![]() $\delta (G)\ge k\gt d$
, the graph
$\delta (G)\ge k\gt d$
, the graph
![]() $G-x$
for some
$G-x$
for some
![]() $x \in V(G)$
has minimum degree at least
$x \in V(G)$
has minimum degree at least
![]() $d$
and thus must contain
$d$
and thus must contain
![]() $F$
as a minor. Let
$F$
as a minor. Let
![]() $X \subseteq V(G)$
be chosen of minimum size subject to
$X \subseteq V(G)$
be chosen of minimum size subject to
![]() $G[X]$
containing
$G[X]$
containing
![]() $F$
as a minor. Note that from the above it follows that
$F$
as a minor. Note that from the above it follows that
![]() $|X|\le{\textrm{v}}(G)-1$
and hence that
$|X|\le{\textrm{v}}(G)-1$
and hence that
![]() $V(G)\setminus X \neq \emptyset$
. Let
$V(G)\setminus X \neq \emptyset$
. Let
![]() $(Z_f)_{f \in V(F)}$
be an
$(Z_f)_{f \in V(F)}$
be an
![]() $F$
-minor model in
$F$
-minor model in
![]() $G[X]$
. By minimality of
$G[X]$
. By minimality of
![]() $X$
, we have that
$X$
, we have that
![]() $(Z_f)_{f \in V(F)}$
forms a partition of
$(Z_f)_{f \in V(F)}$
forms a partition of
![]() $X$
. With the goal of bounding the number of edges in
$X$
. With the goal of bounding the number of edges in
![]() $G-X$
, we present our next argument as a separate claim. We will later use this bound and Turán’s theorem to show the existence of an
$G-X$
, we present our next argument as a separate claim. We will later use this bound and Turán’s theorem to show the existence of an
![]() $F$
-subgraph in
$F$
-subgraph in
![]() $G-X$
.
$G-X$
.
Claim 22.
For every
![]() $v \in V(G)\setminus X$
and every
$v \in V(G)\setminus X$
and every
![]() $f \in V(F)$
, we have
$f \in V(F)$
, we have
![]() $|N(v) \cap Z_f| \lt 9{\textrm{v}}(F)$
.
$|N(v) \cap Z_f| \lt 9{\textrm{v}}(F)$
.
Proof. Let
![]() $v \in V(G)\setminus X$
and
$v \in V(G)\setminus X$
and
![]() $f \in V(F)$
be arbitrary. For
$f \in V(F)$
be arbitrary. For
![]() $|Z_f|=1$
the inequality
$|Z_f|=1$
the inequality
![]() $|N(v) \cap Z_f|\le 1\lt 9{\textrm{v}}(F)$
trivially holds for every
$|N(v) \cap Z_f|\le 1\lt 9{\textrm{v}}(F)$
trivially holds for every
![]() $v \in V(G)\setminus X$
. We may therefore assume
$v \in V(G)\setminus X$
. We may therefore assume
![]() $|Z_f|\ge 2$
. Let
$|Z_f|\ge 2$
. Let
![]() $T_f$
denote a spanning tree of the connected graph
$T_f$
denote a spanning tree of the connected graph
![]() $G[Z_f]$
, and let
$G[Z_f]$
, and let
![]() $L_f\subseteq Z_f$
be the set of leaves in
$L_f\subseteq Z_f$
be the set of leaves in
![]() $T_f$
.
$T_f$
.
We first show that
![]() $T_f$
has at most
$T_f$
has at most
![]() ${\textrm{v}}(F)-1$
leaves. Note that for every
${\textrm{v}}(F)-1$
leaves. Note that for every
![]() $l \in L_f$
the graph
$l \in L_f$
the graph
![]() $G[Z_f\setminus \{l\}]$
is still connected. However, by minimality of
$G[Z_f\setminus \{l\}]$
is still connected. However, by minimality of
![]() $X$
,
$X$
,
![]() $G[X \setminus \{l\}]$
does not contain
$G[X \setminus \{l\}]$
does not contain
![]() $F$
as a minor, and thus in particular the set system consisting of
$F$
as a minor, and thus in particular the set system consisting of
![]() $Z_f\setminus \{l\}$
together with the remaining branch-sets
$Z_f\setminus \{l\}$
together with the remaining branch-sets
![]() $(Z_{f'})_{f' \in V(F), f' \neq f}$
cannot be an
$(Z_{f'})_{f' \in V(F), f' \neq f}$
cannot be an
![]() $F$
-minor model in
$F$
-minor model in
![]() $G$
. In consequence, there has to exist some
$G$
. In consequence, there has to exist some
![]() $f' \in V(F)\setminus \{f\}$
such that among all vertices in
$f' \in V(F)\setminus \{f\}$
such that among all vertices in
![]() $Z_f$
, the vertex
$Z_f$
, the vertex
![]() $l$
is the only one that has a neighbour in
$l$
is the only one that has a neighbour in
![]() $Z_{f'}$
. Since the above argument applies to any choice of
$Z_{f'}$
. Since the above argument applies to any choice of
![]() $l \in L_f$
, and since the respective elements
$l \in L_f$
, and since the respective elements
![]() $f'$
have to be distinct for different choices of
$f'$
have to be distinct for different choices of
![]() $l$
, it follows that
$l$
, it follows that
![]() $|L_f|\le |V(F)\setminus \{f\}|={\textrm{v}}(F)-1$
.
$|L_f|\le |V(F)\setminus \{f\}|={\textrm{v}}(F)-1$
.
We next describe a decomposition of
![]() $T_f$
into strictly less than
$T_f$
into strictly less than
![]() $2{\textrm{v}}(F)$
edge-disjoint and internal-vertex-disjoint paths. Let
$2{\textrm{v}}(F)$
edge-disjoint and internal-vertex-disjoint paths. Let
![]() $T_f'$
be a tree without degree
$T_f'$
be a tree without degree
![]() $2$
-vertices such that
$2$
-vertices such that
![]() $T_f$
is a subdivision of
$T_f$
is a subdivision of
![]() $T_f'$
, i.e., every edge in
$T_f'$
, i.e., every edge in
![]() $T_f'$
corresponds to one maximal path of
$T_f'$
corresponds to one maximal path of
![]() $T_f$
all whose internal vertices are of degree
$T_f$
all whose internal vertices are of degree
![]() $2$
. Then, since
$2$
. Then, since
![]() $T_f'$
is a tree and thus has average degree strictly less than
$T_f'$
is a tree and thus has average degree strictly less than
![]() $2$
, it has more leaves than vertices of degree
$2$
, it has more leaves than vertices of degree
![]() $3$
or more. As the number of leaves in
$3$
or more. As the number of leaves in
![]() $T_f'$
is exactly
$T_f'$
is exactly
![]() $|L_f|$
, we have
$|L_f|$
, we have
![]() ${\textrm{v}}(T_f')\le |L_f|+(|L_f|-1)\le 2{\textrm{v}}(F)-3$
and therefore
${\textrm{v}}(T_f')\le |L_f|+(|L_f|-1)\le 2{\textrm{v}}(F)-3$
and therefore
![]() ${\textrm{e}}(T_f')={\textrm{v}}(T_f')-1\le 2{\textrm{v}}(F)-4\lt 2{\textrm{v}}(F)$
. This means that
${\textrm{e}}(T_f')={\textrm{v}}(T_f')-1\le 2{\textrm{v}}(F)-4\lt 2{\textrm{v}}(F)$
. This means that
![]() $T_f$
can be expressed as the edge-disjoint union of a collection of paths
$T_f$
can be expressed as the edge-disjoint union of a collection of paths
![]() $(P_i)_{i=1}^r$
where
$(P_i)_{i=1}^r$
where
![]() $r\lt 2{\textrm{v}}(F)$
and the internal vertices of each path
$r\lt 2{\textrm{v}}(F)$
and the internal vertices of each path
![]() $P_i$
are of degree
$P_i$
are of degree
![]() $2$
in
$2$
in
![]() $T_f$
.
$T_f$
.
Now choose a vertex set
![]() $Y\subseteq Z_f$
of size at most
$Y\subseteq Z_f$
of size at most
![]() ${\textrm{v}}(F)-1$
as follows: For each edge
${\textrm{v}}(F)-1$
as follows: For each edge
![]() $ff' \in E(F)$
, pick some vertex
$ff' \in E(F)$
, pick some vertex
![]() $y_{f'} \in Z_f$
that has at least one neighbour in
$y_{f'} \in Z_f$
that has at least one neighbour in
![]() $Z_{f'}$
and add it to
$Z_{f'}$
and add it to
![]() $Y$
. Let
$Y$
. Let
![]() $\mathcal{R}$
denote the collection of internally disjoint paths in
$\mathcal{R}$
denote the collection of internally disjoint paths in
![]() $T_f$
obtained from
$T_f$
obtained from
![]() $(P_i)_{i=1}^r$
by splitting each path
$(P_i)_{i=1}^r$
by splitting each path
![]() $P_i$
into its maximal subpaths that do not contain internal vertices in
$P_i$
into its maximal subpaths that do not contain internal vertices in
![]() $Y$
. It is easy to see that
$Y$
. It is easy to see that
![]() $|\mathcal{R}| \le r+|Y|\lt 2{\textrm{v}}(F)+{\textrm{v}}(F)=3{\textrm{v}}(F)$
, and that
$|\mathcal{R}| \le r+|Y|\lt 2{\textrm{v}}(F)+{\textrm{v}}(F)=3{\textrm{v}}(F)$
, and that
![]() $T_f$
equals the union of the paths in
$T_f$
equals the union of the paths in
![]() $\mathcal{R}$
.
$\mathcal{R}$
.
We next claim that for every vertex
![]() $v \in V(G)\setminus X$
and every
$v \in V(G)\setminus X$
and every
![]() $R \in \mathcal{R}$
, we have
$R \in \mathcal{R}$
, we have
![]() $|N(v) \cap V(R)|\le 3$
. Indeed, suppose that
$|N(v) \cap V(R)|\le 3$
. Indeed, suppose that
![]() $v$
has at least
$v$
has at least
![]() $4$
distinct neighbours on
$4$
distinct neighbours on
![]() $R$
. Let
$R$
. Let
![]() $x$
and
$x$
and
![]() $y$
be the two neighbours of
$y$
be the two neighbours of
![]() $v$
on
$v$
on
![]() $R$
that are closest to the endpoints of
$R$
that are closest to the endpoints of
![]() $R$
. Define
$R$
. Define
![]() $R'$
as the path obtained from
$R'$
as the path obtained from
![]() $R$
by replacing its subpath between
$R$
by replacing its subpath between
![]() $x$
and
$x$
and
![]() $y$
(which has to contain at least two internal vertices) by the path
$y$
(which has to contain at least two internal vertices) by the path
![]() $x-v-y$
of length two. Let
$x-v-y$
of length two. Let
![]() $A$
be the set of vertices on
$A$
be the set of vertices on
![]() $R$
strictly between
$R$
strictly between
![]() $x$
and
$x$
and
![]() $y$
and observe that
$y$
and observe that
![]() $|A| \geq 2$
and
$|A| \geq 2$
and
![]() $A \cap Y = \emptyset$
. For
$A \cap Y = \emptyset$
. For
![]() $X'\;:\!=\;(X\setminus A) \cup \{v\}$
we have
$X'\;:\!=\;(X\setminus A) \cup \{v\}$
we have
![]() $|X'|\lt |X|$
and we can find an
$|X'|\lt |X|$
and we can find an
![]() $F$
-minor model in
$F$
-minor model in
![]() $G[X']$
, namely the branch-sets
$G[X']$
, namely the branch-sets
![]() $(Z_f\setminus A) \cup \{x\}$
together with
$(Z_f\setminus A) \cup \{x\}$
together with
![]() $(Z_{f'})_{f' \in V(F), f'\neq f}$
. Notice that
$(Z_{f'})_{f' \in V(F), f'\neq f}$
. Notice that
![]() $G[(Z_f\setminus A) \cup \{x\}]$
is indeed connected as all the internal vertices of
$G[(Z_f\setminus A) \cup \{x\}]$
is indeed connected as all the internal vertices of
![]() $R$
are of degree
$R$
are of degree
![]() $2$
in
$2$
in
![]() $T_f$
. Also, since
$T_f$
. Also, since
![]() $Y\subseteq Z_f\setminus A$
, there still exists a connection from a vertex in
$Y\subseteq Z_f\setminus A$
, there still exists a connection from a vertex in
![]() $(Z_f\setminus A) \cup \{x\}$
(namely,
$(Z_f\setminus A) \cup \{x\}$
(namely,
![]() $y_{f'}$
) to a vertex in
$y_{f'}$
) to a vertex in
![]() $Z_{f'}$
for every edge
$Z_{f'}$
for every edge
![]() $ff'\in E(F)$
. This contradicts our initial choice of
$ff'\in E(F)$
. This contradicts our initial choice of
![]() $X$
and proves that our assumption was wrong, so indeed every vertex
$X$
and proves that our assumption was wrong, so indeed every vertex
![]() $v \in V(G)\setminus X$
satisfies
$v \in V(G)\setminus X$
satisfies
![]() $|N(v) \cap V(R)|\le 3$
for every
$|N(v) \cap V(R)|\le 3$
for every
![]() $R\in \mathcal{R}$
.
$R\in \mathcal{R}$
.
Therefore, we have
![]() $|N(v) \cap Z_f| \le \sum _{R \in \mathcal{R}}{|N(v) \cap V(R)|}\le 3|\mathcal{R}|\lt 9{\textrm{v}}(F)$
for every
$|N(v) \cap Z_f| \le \sum _{R \in \mathcal{R}}{|N(v) \cap V(R)|}\le 3|\mathcal{R}|\lt 9{\textrm{v}}(F)$
for every
![]() $v \in V(G)\setminus X$
, which concludes the proof of the claim.
$v \in V(G)\setminus X$
, which concludes the proof of the claim.
It follows immediately from Claim 22 that
![]() $|N(v) \cap X| \le \sum _{f \in V(F)}{|N(v) \cap Z_f|} \lt 9{\textrm{v}}(F)^2$
for every
$|N(v) \cap X| \le \sum _{f \in V(F)}{|N(v) \cap Z_f|} \lt 9{\textrm{v}}(F)^2$
for every
![]() $v \in V(G)\setminus X$
. Additionally recalling that
$v \in V(G)\setminus X$
. Additionally recalling that
![]() $\delta (G) \ge{\textrm{v}}(F)+k-1\ge k$
, we find that for every
$\delta (G) \ge{\textrm{v}}(F)+k-1\ge k$
, we find that for every
![]() $v \in V(G)\setminus X$
, we have
$v \in V(G)\setminus X$
, we have
![]() $\text{deg}_{G-X}(v)=|N(v) \setminus X|=\text{deg}(v)-|N(v) \cap X|\gt k-9{\textrm{v}}(F)^2$
. Having established
$\text{deg}_{G-X}(v)=|N(v) \setminus X|=\text{deg}(v)-|N(v) \cap X|\gt k-9{\textrm{v}}(F)^2$
. Having established
![]() $V(G)\setminus X \neq \emptyset$
at the beginning of the proof, it now follows that
$V(G)\setminus X \neq \emptyset$
at the beginning of the proof, it now follows that
![]() $G-X$
is a graph of minimum degree greater than
$G-X$
is a graph of minimum degree greater than
![]() $k-9{\textrm{v}}(F)^2$
. Also note that since
$k-9{\textrm{v}}(F)^2$
. Also note that since
![]() $G[X]$
contains
$G[X]$
contains
![]() $F$
as a minor, we are not able to find
$F$
as a minor, we are not able to find
![]() $k$
distinct vertices in
$k$
distinct vertices in
![]() $V(G)\setminus X$
as these could be used to augment the
$V(G)\setminus X$
as these could be used to augment the
![]() $F$
-minor in
$F$
-minor in
![]() $G[X]$
to an
$G[X]$
to an
![]() $H$
-minor in
$H$
-minor in
![]() $G$
, contradicting our assumptions. We thus have
$G$
, contradicting our assumptions. We thus have
![]() ${\textrm{v}}(G-X)\lt k$
. Using our choice of
${\textrm{v}}(G-X)\lt k$
. Using our choice of
![]() $k_0$
and
$k_0$
and
![]() $k \ge k_0$
, it now follows that
$k \ge k_0$
, it now follows that
Therefore,
![]() $G-X$
has more than
$G-X$
has more than
![]() $\bigl (1-\frac{1}{{\textrm{v}}(F)-1}\bigr )\frac{{\textrm{v}}(G-X)^2}{2}$
edges and thus Theorem 20 implies the existence of a clique on
$\bigl (1-\frac{1}{{\textrm{v}}(F)-1}\bigr )\frac{{\textrm{v}}(G-X)^2}{2}$
edges and thus Theorem 20 implies the existence of a clique on
![]() ${\textrm{v}}(F)$
vertices in
${\textrm{v}}(F)$
vertices in
![]() $G-X$
. In particular,
$G-X$
. In particular,
![]() $G-X$
and thus
$G-X$
and thus
![]() $G$
contain a subgraph isomorphic to
$G$
contain a subgraph isomorphic to
![]() $F$
. Let
$F$
. Let
![]() $K \subseteq V(G)$
be the vertex set of such a copy of
$K \subseteq V(G)$
be the vertex set of such a copy of
![]() $F$
. Then, since
$F$
. Then, since
![]() ${\textrm{v}}(G)\ge \delta (G)+1\ge{\textrm{v}}(F)+k$
, there are at least
${\textrm{v}}(G)\ge \delta (G)+1\ge{\textrm{v}}(F)+k$
, there are at least
![]() $k$
vertices outside of
$k$
vertices outside of
![]() $K$
in
$K$
in
![]() $G$
, which can be added to the copy of
$G$
, which can be added to the copy of
![]() $F$
on vertex set
$F$
on vertex set
![]() $K$
to create a subgraph of
$K$
to create a subgraph of
![]() $G$
that is isomorphic to
$G$
that is isomorphic to
![]() $H$
. In particular, this means that
$H$
. In particular, this means that
![]() $G$
contains
$G$
contains
![]() $H$
as a minor, a contradiction. All in all, we find that our initial assumption, namely regarding the existence of a smallest counterexample
$H$
as a minor, a contradiction. All in all, we find that our initial assumption, namely regarding the existence of a smallest counterexample
![]() $G$
to our claim, was wrong. This concludes the proof that all
$G$
to our claim, was wrong. This concludes the proof that all
![]() $H$
-minor-free graphs are
$H$
-minor-free graphs are
![]() $({\textrm{v}}(H)-2)$
-degenerate.
$({\textrm{v}}(H)-2)$
-degenerate.
It is a well-known fact and easy to prove by induction that for every
![]() $a \in \mathbb{N}$
all
$a \in \mathbb{N}$
all
![]() $a$
-degenerate graphs are
$a$
-degenerate graphs are
![]() $(a+1)$
-choosable. Thus what we have proved also implies that every
$(a+1)$
-choosable. Thus what we have proved also implies that every
![]() $H$
-minor-free graph is
$H$
-minor-free graph is
![]() $({\textrm{v}}(H)-1)$
-choosable, as desired. All in all, it follows that
$({\textrm{v}}(H)-1)$
-choosable, as desired. All in all, it follows that
![]() $f_\ell (H)={\textrm{v}}(H)-1$
, concluding the proof of the theorem.
$f_\ell (H)={\textrm{v}}(H)-1$
, concluding the proof of the theorem.