Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Dembo, Amir
and
Lubetzky, Eyal
2018.
A large deviation principle for the Erdős–Rényi uniform random graph.
Electronic Communications in Probability,
Vol. 23,
Issue. none,
Goldschmidt, Christina
Griffiths, Simon
and
Scott, Alex
2020.
Moderate deviations of subgraph counts in the Erdős-Rényi random graphs 𝐺(𝑛,𝑚) and 𝐺(𝑛,𝑝).
Transactions of the American Mathematical Society,
Vol. 373,
Issue. 8,
p.
5517.
Bhattacharya, Bhaswar B.
and
Ganguly, Shirshendu
2020.
Upper Tails for Edge Eigenvalues of Random Graphs.
SIAM Journal on Discrete Mathematics,
Vol. 34,
Issue. 2,
p.
1069.
Cook, Nicholas
and
Dembo, Amir
2020.
Large deviations of subgraph counts for sparse Erdős–Rényi graphs.
Advances in Mathematics,
Vol. 373,
Issue. ,
p.
107289.
Mukherjee, Somabha
and
Bhattacharya, Bhaswar B.
2020.
Replica symmetry in upper tails of mean-field hypergraphs.
Advances in Applied Mathematics,
Vol. 119,
Issue. ,
p.
102047.
Bhattacharya, Bhaswar B
Ganguly, Shirshendu
Shao, Xuancheng
and
Zhao, Yufei
2020.
Upper Tail Large Deviations for Arithmetic Progressions in a Random Set.
International Mathematics Research Notices,
Vol. 2020,
Issue. 1,
p.
167.
Bhattacharya, Sohom
and
Dembo, Amir
2021.
Upper tail for homomorphism counts in constrained sparse random graphs.
Random Structures & Algorithms,
Vol. 59,
Issue. 3,
p.
315.
Liu, Yang P.
and
Zhao, Yufei
2021.
On the upper tail problem for random hypergraphs.
Random Structures & Algorithms,
Vol. 58,
Issue. 2,
p.
179.
Giardinà, Cristian
Giberti, Claudio
and
Magnanini, Elena
2021.
Approximating the Cumulant Generating Function of Triangles in the Erdös–Rényi Random Graph.
Journal of Statistical Physics,
Vol. 182,
Issue. 2,
Harel, Matan
Mousset, Frank
and
Samotij, Wojciech
2022.
Upper tails via high moments and entropic stability.
Duke Mathematical Journal,
Vol. 171,
Issue. 10,
Neeman, Joe
Radin, Charles
and
Sadun, Lorenzo
2023.
Moderate deviations in cycle count.
Random Structures & Algorithms,
Vol. 63,
Issue. 3,
p.
779.
Kozma, Gady
and
Samotij, Wojciech
2023.
Lower tails via relative entropy.
The Annals of Probability,
Vol. 51,
Issue. 2,
Alvarado, José
Do, Gabriel
and
Griffiths, Simon
2023.
Moderate deviations of triangle counts – the lower tail.
p.
28.
Cook, Nicholas A.
Dembo, Amir
and
Pham, Huy Tuan
2024.
Regularity method and large deviation principles for the Erdős–Rényi hypergraph.
Duke Mathematical Journal,
Vol. 173,
Issue. 5,
Chin, Byron
2025.
Structure of Lower Tails in Sparse Random Graphs.
Random Structures & Algorithms,
Vol. 67,
Issue. 1,
Alvarado, José D.
do Couto, Gabriel Dias
and
Griffiths, Simon
2025.
Moderate deviations of triangle counts in the Erdős-Rényi random graph G(n,m): The lower tail.
European Journal of Combinatorics,
Vol. 129,
Issue. ,
p.
104189.
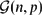 $\mathcal{G}(n,p)$ . We are interested in estimating the lower tail probability
$\mathcal{G}(n,p)$ . We are interested in estimating the lower tail probability 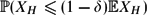 $\mathbb{P}(X_H \le (1-\delta) \mathbb{E} X_H)$ for fixed 0 < δ < 1.
$\mathbb{P}(X_H \le (1-\delta) \mathbb{E} X_H)$ for fixed 0 < δ < 1.
