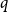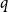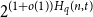Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Behague, Natalie
Hyde, Joseph
Morrison, Natasha
Noel, Jonathan A.
and
Wright, Ashna
2025.
An Approximate Counting Version of the Multidimensional Szemerédi Theorem.
Combinatorica,
Vol. 45,
Issue. 4,