Article contents
On the peel number and the leaf-height of Galton–Watson trees
Published online by Cambridge University Press: 09 June 2022
Abstract
We study several parameters of a random Bienaymé–Galton–Watson tree 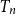 $T_n$ of size
$T_n$ of size  $n$ defined in terms of an offspring distribution
$n$ defined in terms of an offspring distribution 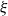 $\xi$ with mean
$\xi$ with mean 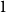 $1$ and nonzero finite variance
$1$ and nonzero finite variance 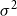 $\sigma ^2$. Let
$\sigma ^2$. Let 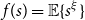 $f(s)=\mathbb{E}\{s^\xi \}$ be the generating function of the random variable
$f(s)=\mathbb{E}\{s^\xi \}$ be the generating function of the random variable 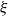 $\xi$. We show that the independence number is in probability asymptotic to
$\xi$. We show that the independence number is in probability asymptotic to 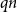 $qn$, where
$qn$, where 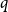 $q$ is the unique solution to
$q$ is the unique solution to 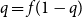 $q = f(1-q)$. One of the many algorithms for finding the largest independent set of nodes uses a notion of repeated peeling away of all leaves and their parents. The number of rounds of peeling is shown to be in probability asymptotic to
$q = f(1-q)$. One of the many algorithms for finding the largest independent set of nodes uses a notion of repeated peeling away of all leaves and their parents. The number of rounds of peeling is shown to be in probability asymptotic to 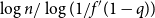 $\log n/\log (1/f'(1-q))$. Finally, we study a related parameter which we call the leaf-height. Also sometimes called the protection number, this is the maximal shortest path length between any node and a leaf in its subtree. If
$\log n/\log (1/f'(1-q))$. Finally, we study a related parameter which we call the leaf-height. Also sometimes called the protection number, this is the maximal shortest path length between any node and a leaf in its subtree. If 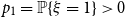 $p_1 = \mathbb{P}\{\xi =1\}\gt 0$, then we show that the maximum leaf-height over all nodes in
$p_1 = \mathbb{P}\{\xi =1\}\gt 0$, then we show that the maximum leaf-height over all nodes in 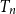 $T_n$ is in probability asymptotic to
$T_n$ is in probability asymptotic to 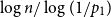 $\log n/\log (1/p_1)$. If
$\log n/\log (1/p_1)$. If 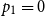 $p_1 = 0$ and
$p_1 = 0$ and  $\kappa$ is the first integer
$\kappa$ is the first integer 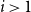 $i\gt 1$ with
$i\gt 1$ with 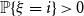 $\mathbb{P}\{\xi =i\}\gt 0$, then the leaf-height is in probability asymptotic to
$\mathbb{P}\{\xi =i\}\gt 0$, then the leaf-height is in probability asymptotic to 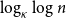 $\log _\kappa \log n$.
$\log _\kappa \log n$.
MSC classification
Information
- Type
- Paper
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press
References
- 1
- Cited by


