No CrossRef data available.
Article contents
On the smallest gap in a sequence with Poisson pair correlations
Published online by Cambridge University Press: 21 November 2024
Abstract
We prove that any increasing sequence of real numbers with average gap 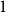 $1$ and Poisson pair correlations has some gap that is at least
$1$ and Poisson pair correlations has some gap that is at least 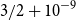 $3/2+10^{-9}$. This improves upon a result of Aistleitner, Blomer, and Radziwiłł.
$3/2+10^{-9}$. This improves upon a result of Aistleitner, Blomer, and Radziwiłł.
Keywords
MSC classification
Information
- Type
- Paper
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press
Footnotes
*
Zachary Chase is partially supported by Ben Green’s Simons Investigator Grant 376201 and gratefully acknowledges the support of the Simons Foundation.
References
Aistleitner, C., Blomer, V. and Radziwiłł, M. (2024) Triple correlation and long gaps in the spectrum of flat tori. J. Eur. Math. Soc. 26(1) 41–74.CrossRefGoogle Scholar
Aistleitner, C., Lachmann, T. and Pausinger, F. (2018) Pair correlations and equidistribution. J. Num. Theory 182 206–220.CrossRefGoogle Scholar
Aistleitner, C., Larcher, G. and Lewko, M. (2017) Additive energy and the Hausdorff dimension of the exceptional set in metric pair correlation problems, with an Appendix by Jean Bourgain. Israel J. Math. 222(1) 463–485.CrossRefGoogle Scholar
Eskin, A., Margulis, G. and Mozes, S. (2005) Quadratic forms of signature (2, 2) and eigenvalue spacings on rectangular 2-tori. Ann. Math. 161 679–725.CrossRefGoogle Scholar
Heath-Brown, D. R. (2010) Pair correlation for fractional parts of
 $\alpha n^2$
, Math. Proc. Cambridge Philos. Soc. 148 385–407.CrossRefGoogle Scholar
$\alpha n^2$
, Math. Proc. Cambridge Philos. Soc. 148 385–407.CrossRefGoogle Scholar
Kuipers, L. and Niederreiter, H. (2006) Uniform distribution of sequences. Dover Publications, Mineola, NY
Google Scholar
Rudnick, Z. and Sarnak, P. (1998) The pair correlation function of fractional parts of polynomials. Comm. Math. Phys. 194(1) 61–70.CrossRefGoogle Scholar
Rudnick, Z. and Zaharescu, A. (1999) A metric result on the pair correlation of fractional parts of sequences,. Acta Arith. 89(3) 283–293.CrossRefGoogle Scholar
Rudnick, Z. and Zaharescu, A. (2002) The distribution of spacings between fractional parts of lacunary sequences. Forum Math. 14(5) 691–712.CrossRefGoogle Scholar
Sarnak, P. (1997) Values at integers of binary quadratic forms. Harmonic analysis and number theory (Montreal 1996), 181-203, CMS Conf. Providence, RI.: Amer. Math. Soc., Proc. 21.Google Scholar
Steinerberger, S. (2018) Poissonian pair correlation and discrepancy,. Indag. Math. 29 1167–1178.CrossRefGoogle Scholar
Walker, A. (2018) The Primes are not metric Poissonian. Mathematika 64, 230–236.CrossRefGoogle Scholar


