Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-28T13:16:14.708Z Has data issue: false hasContentIssue false
  • English
  • Français

On the Spread of Random Graphs

Published online by Cambridge University Press:  13 June 2014

LOUIGI ADDARIO-BERRY ,
SVANTE JANSON  and
COLIN McDIARMID
LOUIGI ADDARIO-BERRY
Affiliation:
Department of Mathematics and Statistics, McGill University, 805 Sherbrooke Street West, Montréal, Québec, H3A 2K6, Canada (e-mail: louigi@gmail.comhttp://www.math.mcgill.ca/mytildelouigi/
SVANTE JANSON
Affiliation:
Department of Mathematics, Uppsala University, PO Box 480, SE-751 06 Uppsala, Sweden (e-mail: svante.janson@math.uu.sehttp://www.math.uu.se/mytildesvante/
COLIN McDIARMID
Affiliation:
Department of Statistics, University of Oxford, 1 South Parks Road, Oxford OX1 3TG, UK (e-mail: cmcd@stats.ox.ac.ukhttp://www.stats.ox.ac.uk/mytildecmcd/
Get access Rights & Permissions [Opens in a new window]

Abstract

The spread of a connected graph G was introduced by Alon, Boppana and Spencer [1], and measures how tightly connected the graph is. It is defined as the maximum over all Lipschitz functions f on V(G) of the variance of f(X) when X is uniformly distributed on V(G). We investigate the spread for certain models of sparse random graph, in particular for random regular graphs G(n,d), for Erdős–Rényi random graphs Gn,p in the supercritical range p>1/n, and for a ‘small world’ model. For supercritical Gn,p, we show that if p=c/n with c>1 fixed, then with high probability the spread of the giant component is bounded, and we prove corresponding statements for other models of random graphs, including a model with random edge lengths. We also give lower bounds on the spread for the barely supercritical case when p=(1+o(1))/n. Further, we show that for d large, with high probability the spread of G(n,d) becomes arbitrarily close to that of the complete graph 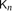$\mathsf{K}_n$.

Keywords

60C05
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 23 , Issue 4 , July 2014 , pp. 477 - 504
Copyright
Copyright © Cambridge University Press 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Alon, N., Boppana, R. and Spencer, J. (1998) An asymptotic isoperimetric inequality. Geom. Funct. Anal. 8 411–436.Google Scholar
[2]Benjamini, I., Kozma, G. and Wormald, N. C. (2014) The mixing time of the giant component of a random graph. Random Struct. Alg. doi:10.1002/rsa.20539.Google Scholar
[3]Bobkov, S. G., Houdré, C. and Tetali, P. (2006) The subgaussian constant and concentration inequalities. Israel J. Math. 156 255–283.Google Scholar
[4]Bollobás, B. (2001) Random Graphs, second edition, Vol. 73 of Cambridge Studies in Advanced Mathematics, Cambridge University Press.Google Scholar
[5]Ding, J., Kim, J. H., Lubetzky, E. and Peres, Y. (2010) Diameters in supercritical random graphs via first passage percolation. Combin. Probab. Comput. 19 729–751.Google Scholar
[6]Dubhashi, D. and Ranjan, D. (1998) Balls and bins: A study in negative dependence. Random Struct. Alg. 13 99–124.Google Scholar
[7]Durrett, R. (2010) Random Graph Dynamics, Cambridge University Press.Google Scholar
[8]Janson, S. and Luczak, M. J. (2007) A simple solution to the k-core problem. Random Struct. Alg. 30 50–62.Google Scholar
[9]Janson, S., Knuth, D. E., Łuczak, T. and Pittel, B. (1993) The birth of the giant component. Random Struct. Alg. 4 231–358.Google Scholar
[10]Janson, S., Łuczak, T. and Rucinski, A. (2000) Random Graphs, Wiley.Google Scholar
[11]Joag-Dev, K. and Proschan, F. (1983) Negative association of random variables, with applications. Ann. Statist. 11 286–295.Google Scholar
[12]Kolchin, V. F. (1986) Random Mappings, Translation Series in Mathematics and Engineering, Optimization Software Inc., New York. Translated from the Russian.Google Scholar
[13]Łuczak, T. (1990) Component behavior near the critical point of the random graph process. Random Struct. Alg. 1 287–310.Google Scholar
[14]Łuczak, T. (1991) Size and connectivity of the k-core of a random graph. Discrete Math. 91 61–68.Google Scholar
[15]Łuczak, T. (1991) Cycles in a random graph near the critical point. Random Struct. Alg. 2 421–439.Google Scholar
[16]Newman, M. E. J. and Watts, D. J. (1999) Renormalization group analysis of the small-world network model. Phys. Lett. A 263 341–346.Google Scholar
[17]Pavlov, Y. L. (1977) The asymptotic distribution of maximum tree size in a random forest (in Russian). Teor. Verojatnost. i Primenen. 22 523–533. English translation in Theoret. Probab. Appl. 22 (1977) 509–520.Google Scholar
[18]Pavlov, Y. L. (1996) Random Forests (in Russian), Karelian Centre Russian Academy of Sciences, Petrozavodsk. English translation (2000), VSP, Zeist.Google Scholar
[19]Riordan, O. and Wormald, N. C. (2010) The diameter of sparse random graphs. Combin. Probab. Comput. 19 835–926.Google Scholar
[20]Walkup, D. W. (1980) Matchings in random regular bipartite digraphs. Discrete Math. 31 59–64.Google Scholar
[21]Watts, D. J. and Strogatz, S. H. (1998) Collective dynamics of ‘small-world’ networks. Nature 393 440–442.Google Scholar