Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-11T14:08:20.219Z Has data issue: false hasContentIssue false
  • English
  • Français

Parking on a Random Tree

Part of: Equilibrium statistical mechanics Graph theory Markov processes Combinatorial probability

Published online by Cambridge University Press:  23 October 2018

CHRISTINA GOLDSCHMIDT  and
MICHAŁ PRZYKUCKI
CHRISTINA GOLDSCHMIDT
Affiliation:
Department of Statistics, University of Oxford, 24–29 St Giles', Oxford OX1 3LB, UK Lady Margaret Hall, Norham Gardens, Oxford OX2 6QA, UK (e-mail: goldschm@stats.ox.ac.uk)
MICHAŁ PRZYKUCKI
Affiliation:
School of Mathematics, University of Birmingham, Edgbaston, Birmingham B15 2TT, UK (e-mail: m.j.przykucki@bham.ac.uk)
Get access Rights & Permissions [Opens in a new window]

Abstract

Consider a uniform random rooted labelled tree on n vertices. We imagine that each node of the tree has space for a single car to park. A number m ≤ n of cars arrive one by one, each at a node chosen independently and uniformly at random. If a car arrives at a space which is already occupied, it follows the unique path towards the root until it encounters an empty space, in which case it parks there; if there is no empty space, it leaves the tree. Consider m = ⌊α n⌋ and let An,α denote the event that all ⌊α n⌋ cars find spaces in the tree. Lackner and Panholzer proved (via analytic combinatorics methods) that there is a phase transition in this model. Then if α ≤ 1/2, we have 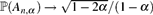$\mathbb{P}({A_{n,\alpha}}) \to {\sqrt{1-2\alpha}}/{(1-\alpha})$, whereas if α > 1/2 we have 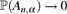$\mathbb{P}({A_{n,\alpha}}) \to 0$. We give a probabilistic explanation for this phenomenon, and an alternative proof via the objective method. Along the way, we consider the following variant of the problem: take the tree to be the family tree of a Galton–Watson branching process with Poisson(1) offspring distribution, and let an independent Poisson(α) number of cars arrive at each vertex. Let X be the number of cars which visit the root of the tree. We show that 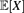$\mathbb{E}{[X]}$ undergoes a discontinuous phase transition, which turns out to be a generic phenomenon for arbitrary offspring distributions of mean at least 1 for the tree and arbitrary arrival distributions.

MSC classification

Primary: 60C05: Combinatorial probability
Secondary: 60J80: Branching processes (Galton-Watson, birth-and-death, etc.) 05C05: Trees 82B26: Phase transitions (general)
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 28 , Issue 1 , January 2019 , pp. 23 - 45
Copyright
Copyright © Cambridge University Press 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Research supported by EPSRC Fellowship EP/N004833/1.

References

[1] Abraham, R. and Delmas, J.-F. (2015) An introduction to Galton–Watson trees and their local limits. Lecture notes available at arXiv:1506.05571.Google Scholar
[2] Addario-Berry, L. (2013) The local weak limit of the minimum spanning tree of the complete graph. arXiv:1301.1667Google Scholar
[3] Aldous, D. J. and Bandyopadhyay, A. (2005) A survey of max-type recursive distributional equations. Ann. Appl. Probab. 15 1047–1110.Google Scholar
[4] Aldous, D. and Steele, J. (2004) The objective method: Probabilistic combinatorial optimization and local weak convergence. In Probability on Discrete Structures (Kesten, H., ed.), Vol. 110 of Encyclopaedia of Mathematical Sciences, Springer, pp. 1–72.Google Scholar
[5] Barlow, M. T. and Kumagai, T. (2006) Random walk on the incipient infinite cluster on trees. Illinois J. Math. 50 33–65.Google Scholar
[6] Benjamini, I. and Schramm, O. (2001) Recurrence of distributional limits of finite planar graphs. Electron. J. Probab. 6 23.Google Scholar
[7] Brown, M., Peköz, E. and Ross, S. (2010) Some results for skip-free random walk. Probab. Eng. Inform. Sci. 24 491–507.Google Scholar
[8] Corless, R. M., Gonnet, G. H., Hare, D. E. G., Jeffrey, D. J. and Knuth, D. E. (1996) On the Lambert W function. Adv. Comput. Math. 5 329–359.Google Scholar
[9] Grimmett, G. (1980) Random labelled trees and their branching networks. J. Austral. Math. Soc. 30 229–237.Google Scholar
[10] Jones, O. (2018) Runoff on rooted trees. arXiv:1807.08803Google Scholar
[11] Kesten, H. (1986) Subdiffusive behavior of random walk on a random cluster. Ann. Inst. H. Poincaré Probab. Statist. 22 425–487.Google Scholar
[12] Konheim, A. and Weiss, B. (1966) An occupancy discipline and applications. SIAM J. Appl. Math. 14 1266–1274.Google Scholar
[13] Lackner, M.-L. and Panholzer, A. (2016) Parking functions for mappings. J. Combin. Theory Ser. A 142 1–28.Google Scholar
[14] Luczak, M. and Winkler, P. (2004) Building uniformly random subtrees. Random Struct. Alg. 24 420–443.Google Scholar
[15] Lyons, R., Peled, R. and Schramm, O. (2008) Growth of the number of spanning trees of the Erdős–Rényi giant component. Combin. Probab. Comput. 17 711–726.Google Scholar
[16] Stanley, R. (1996) Hyperplane arrangements, interval orders, and trees. Proc. Natl Acad. Sci. 93 2620–2625.Google Scholar
[17] Stanley, R. (1997) Parking functions and noncrossing partitions. Electron. J. Combin. 4 1–14.Google Scholar
[18] Stanley, R. (1997 & 1999) Enumerative Combinatorics, Vols I & II, Cambridge University Press.Google Scholar
[19] Stanley, R. (1998) Hyperplane arrangements, parking functions and tree inversions. In Mathematical Essays in honor of Gian-Carlo Rota (Sagan, B. and Stanley, R., eds), Vol. 161 of Progress in Mathematics, Springer, pp. 359–375.Google Scholar