Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-28T13:41:06.705Z Has data issue: false hasContentIssue false
  • English
  • Français

Partially Observed Boolean Sequences and Noise Sensitivity

Published online by Cambridge University Press:  13 February 2014

DANIEL AHLBERG
DANIEL AHLBERG*
Affiliation:
Mathematical Sciences Research Institute, 17 Gauss Way, Berkeley, CA 94720-5070, USA (e-mail: dahlberg@msri.org)
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 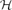${\mathcal H}$ denote a collection of subsets of {1,2,. . .,n}, and assign independent random variables uniformly distributed over [0,1] to the n elements. Declare an element p-present if its corresponding value is at most p. In this paper, we quantify how much the observation of the r-present (r>p) set of elements affects the probability that the set of p-present elements is contained in 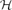${\mathcal H}$. In the context of percolation, we find that this question is closely linked to the near-critical regime. As a consequence, we show that for every r>1/2, bond percolation on the subgraph of the square lattice given by the set of r-present edges is almost surely noise sensitive at criticality, thus generalizing a result due to Benjamini, Kalai and Schramm.

Keywords

Primary 60C05Secondary 60K3506E30
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 23 , Issue 3 , May 2014 , pp. 317 - 330
Copyright
Copyright © Cambridge University Press 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Ahlberg, D., Broman, E., Griffiths, S. and Morris, R. (2014) Noise sensitivity in continuum percolation. Israel J. Math., (accepted).CrossRefGoogle Scholar
[2]Benjamini, I., Kalai, G. and Schramm, O. (1999) Noise sensitivity of Boolean functions and applications to percolation. Inst. Hautes Études Sci. Publ. Math. 90 5–43.Google Scholar
[3]Bey, C. (2003) An upper bound on the sum of squares of degrees in a hypergraph. Discrete Math. 269 259–263.Google Scholar
[4]Bollobás, B. and Riordan, O. (2006) Percolation, Cambridge University Press.Google Scholar
[5]Garban, C., Pete, G. and Schramm, O. (2010) The Fourier spectrum of critical percolation. Acta Math. 205 19–104.CrossRefGoogle Scholar
[6]Garban, C. and Steif, J. E. (2012) Noise sensitivity and percolation. In Probability and Statistical Physics in Two and More Dimensions, Vol. 15 of Clay Mathematics Proceedings, AMS, pp. 49–154.Google Scholar
[7]Kahn, J., Kalai, G. and Linial, N. (1988) The influence of variables on Boolean functions. In 29th Annual Symposium on Foundations of Computer Science, pp. 68–80.CrossRefGoogle Scholar
[8]Kesten, H. (1987) Scaling relations for 2D-percolation. Comm. Math. Phys. 109 109–156.Google Scholar
[9]Nolin, P. (2008) Near-critical percolation in two dimensions. Electron. J. Probab. 13 1562–1623.CrossRefGoogle Scholar
[10]Schramm, O. and Steif, J. E. (2010) Quantitative noise sensitivity and exceptional times for percolation. Ann. of Math. (2) 171 619–672.Google Scholar
[11]Smirnov, S. and Werner, W. (2001) Critical exponents for two-dimensional percolation. Math. Res. Lett. 8 729–744.CrossRefGoogle Scholar