Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-28T12:52:43.881Z Has data issue: false hasContentIssue false
  • English
  • Français

Perfect Matchings in Random r-regular, s-uniform Hypergraphs

Published online by Cambridge University Press:  12 September 2008

Colin Cooper ,
Alan Frieze ,
Michael Molloy  and
Bruce Reed
Colin Cooper
Affiliation:
School of Mathematical Sciences, University of North London, London, UK
Alan Frieze
Affiliation:
Department of Mathematics, Carnegie Mellon University, Pittsburgh, PA 15213, USA
Michael Molloy
Affiliation:
Department of Mathematics, Carnegie Mellon University, Pittsburgh, PA 15213, USA
Bruce Reed
Affiliation:
Department of Mathematics, Carnegie Mellon University, Pittsburgh, PA 15213, USA
Get access Rights & Permissions [Opens in a new window]

Abstract

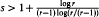We show that r-regular, s-uniform hypergraphs contain a perfect matching with high probability (whp), provided The Proof is based on the application of a technique of Robinson and Wormald [7, 8]. The space of hypergraphs is partitioned into subsets according to the number of small cycles in the hypergraph. The difference in the expected number of perfect matchings between these subsets explains most of the variance of the number of perfect matchings in the space of hypergraphs, and is sufficient to prove existence (whp), using the Chebychev Inequality.

Type
Research Article
Information
Combinatorics, Probability and Computing , Volume 5 , Issue 1 , March 1996 , pp. 1 - 14
Copyright
Copyright © Cambridge University Press 1996

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Alon, N. and Spencer, J. H. (1992) The Probabilistic Method, Wiley, New York.Google Scholar
[2]Bender, E. A. and Canfield, E. R. (1978) The asymptotic number of labelled graphs with given degree sequences. J. Combinatorial Theory, Series A 24 296–307.CrossRefGoogle Scholar
[3]Bollobás, B. (1980) A probabilistic proof of an asymptotic formula for the number of labelled regular graphs. Euro. J. Combinatorics 1 311–316.CrossRefGoogle Scholar
[4]Erdős, P. and Rényi, A. (1966) On the existence of a factor of degree one of a connected random graph. Acta Math. Acad. Sci. Hungar. 17 359–368.CrossRefGoogle Scholar
[5]Frieze, A. M. and Janson, S. (1995) Perfect matchings in random s-uniform hypergraphs. Random Structures and Algorithms 7 41–57.CrossRefGoogle Scholar
[6]Łuczak, and Ruciński, A. (1991) Tree matchings in random graph processes. SIAM J. Discrete Math. 4 107–120.CrossRefGoogle Scholar
[7]Robinson, R. W. and Wormald, N. C. (1992) Almost all cubic graphs are Hamiltonian. Random Structures and Algorithms 3 117–126.CrossRefGoogle Scholar
[8]Robinson, R. W. and Wormald, N. C. (1994) Almost all regular graphs are Hamiltonian. Random Structures and Algorithms 5 363–374.CrossRefGoogle Scholar
[9]Ruciński, A. (1992) Matching and covering the vertices of a random graph by copies of a given graph. Discrete Math. 105 185–197.CrossRefGoogle Scholar
[10]Schmidt, J. and Shamir, E. (1983) A threshold for perfect matchings in random d-pure hypergraphs. Discrete Math. 45 287–295.CrossRefGoogle Scholar