Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-28T00:08:53.543Z Has data issue: false hasContentIssue false
  • English
  • Français

Permutations with equal orders

Part of: Combinatorial probability

Published online by Cambridge University Press:  27 January 2021

Huseyin Acan ,
Charles Burnette ,
Sean Eberhard ,
Eric Schmutz  and
James Thomas
Huseyin Acan
Affiliation:
Department of Mathematics, Drexel University, Philadelphia, PA 19104, USA
Charles Burnette
Affiliation:
Mathematics Department, Xavier University of Louisiana, New Orleans, LA 70125, USA
Sean Eberhard
Affiliation:
Department of Pure Mathematics and Mathematical Statistics, Centre for Mathematical Sciences, University of Cambridge, Cambridge CB3 0WB, UK
Eric Schmutz*
Affiliation:
Department of Mathematics, Drexel University, Philadelphia, PA 19104, USA
James Thomas
Affiliation:
Department of Mathematics, Drexel University, Philadelphia, PA 19104, USA
*
*Corresponding author. Email: schmutze@drexel.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 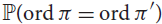${\mathbb{P}}(ord\pi = ord\pi ')$ be the probability that two independent, uniformly random permutations of [n] have the same order. Answering a question of Thibault Godin, we prove that 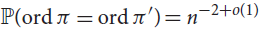${\mathbb{P}}(ord\pi = ord\pi ') = {n^{ - 2 + o(1)}}$ and that 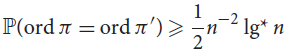${\mathbb{P}}(ord\pi = ord\pi ') \ge {1 \over 2}{n^{ - 2}}lg*n$ for infinitely many n. (Here lg*n is the height of the tallest tower of twos that is less than or equal to n.)

MSC classification

Primary: 60C05: Combinatorial probability
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 30 , Issue 5 , September 2021 , pp. 800 - 810
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arratia, R., Barbour, A. D. and Tavaré, S. (2003) Logarithmic Combinatorial Structures: A Probabilistic Approach, EMS Monographs in Mathematics. European Mathematical Society (EMS).Google Scholar
Devroye, L. (1988) Applications of the theory of records in the study of random trees. Acta Inform. 26 123–130.CrossRefGoogle Scholar
Erdős, P. and Turán, P. (1967) On some problems of a statistical group-theory, III. Acta Math. Acad. Sci. Hungar. 18 309–320.CrossRefGoogle Scholar
Erdős, P. and Turán, P. (1968) On some problems of a statistical group-theory, IV. Acta Math. Acad. Sci. Hungar. 19 413–435.CrossRefGoogle Scholar
Flajolet, P., Fusy, E., Gourdon, X., Panario, D. and Pouyanne, N. (2006) A hybrid of Darboux’s method and singularity analysis in combinatorial asymptotics. Electron. J. Combin. 13 R103.CrossRefGoogle Scholar
Ford, K. Anatomy of integers and random permutations course lecture notes. https://faculty.math.illinois.edu/˜ford/Anatomy_lectnotes.pdf Google Scholar
Godin, T. (2017) An analogue to Dixon’s theorem for automaton groups. In 2017 Proceedings of the Fourteenth Workshop on Analytic Algorithmics and Combinatorics (ANALCO), pp. 164–173. SIAM.10.1137/1.9781611974775.17CrossRefGoogle Scholar
Gowers, W. T. (2000) The two cultures of mathematics. In Mathematics: Frontiers and Perspectives (Arnold, V. et al., eds), pp. 65–78. AMS.Google Scholar
Granville, A. The anatomy of integers and permutations. https://www.dms.umontreal.ca/˜andrew/MSI/AnatomyForTheBook.pdf Google Scholar
Hall, R. R. and Tenenbaum, G. (1988) Divisors, Vol. 90 of Cambridge Tracts in Mathematics. Cambridge University Press.10.1017/CBO9780511566004CrossRefGoogle Scholar
Niemeyer, A. C. and Praeger, C. E. (2007) On permutations of order dividing a given integer. J. Algebraic Combin. 26 125–142.CrossRefGoogle Scholar
Niemeyer, A. C., Praeger, C. E. and Seress, A. (2013) Estimation problems and randomised group algorithms. In Probabilistic Group Theory, Combinatorics, and Computing, Vol. 2070 of Lecture Notes in Mathematics, pp. 35–82. Springer.CrossRefGoogle Scholar
Pemantle, R. and Wilson, M. C. (2013) Analytic Combinatorics in Several Variables, Vol. 140 of Cambridge Studies in Advanced Mathematics. Cambridge University Press.Google Scholar
Raichev, A. (2011) New software for computing asymptotics of multivariate generating functions. ACM Commun. Comput. Algebra 45 183–185.Google Scholar
Thibo (2016) ‘What is the probability that two random permutations have the same order?’, math overflow. http://mathoverflow.net/a/230276 Google Scholar
Thomas, J. (2020) Three problems in the asymptotic order of group elements. PhD thesis, Drexel University.Google Scholar
Warlimont, R. (1978) Über die Anzahl der Lősungen von x n = 1 in der symmetrischen Gruppe S n. Arch. Math. (Basel) 30 591–594.Google Scholar
Wilf, H. S. (1986) The asymptotics of e P(z) and the number of elements of each order in S n. Bull. Amer. Math. Soc. (N.S.) 15 228–232.Google Scholar