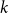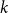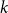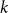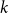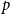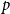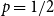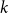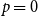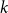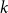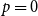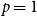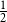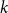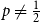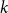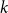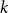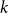Polarised random $k$-SAT

Abstract

In this paper we study a variation of the random $k$-SAT problem, called polarised random $k$-SAT, which contains both the classical random $k$-SAT model and the random version of monotone $k$-SAT another well-known NP-complete version of SAT. In this model there is a polarisation parameter $p$, and in half of the clauses each variable occurs negated with probability $p$ and pure otherwise, while in the other half the probabilities are interchanged. For $p=1/2$ we get the classical random $k$-SAT model, and at the other extreme we have the fully polarised model where $p=0$, or 1. Here there are only two types of clauses: clauses where all $k$ variables occur pure, and clauses where all $k$ variables occur negated. That is, for $p=0$, and $p=1$, we get an instance of random monotone $k$-SAT.

We show that the threshold of satisfiability does not decrease as $p$ moves away from $\frac{1}{2}$ and thus that the satisfiability threshold for polarised random $k$-SAT with $p\neq \frac{1}{2}$ is an upper bound on the threshold for random $k$-SAT. Hence the satisfiability threshold for random monotone $k$-SAT is at least as large as for random $k$-SAT, and we conjecture that asymptotically, for a fixed $k$, the two thresholds coincide.

1. Introduction

1.1. Random $\textrm{k}$ -SAT

During the last decades the random $k$ -SAT problem has been the focus for a large amount of work by both computer scientists, mathematicians and physicists. In the classic version of this problem we have $n$ Boolean variables and $m$ random clauses, with $k$ variables each, giving us a random $k$ -CNF formula $\Phi$ . The clauses are chosen uniformly at random among all the $2^k\binom{n}{k}$ possible such clauses. It is known that if $\alpha =\frac{m}{n}$ is small enough then $\Phi$ is satisfiable w.h.p. (asymptotically as $n\to \infty$ ) and if $\alpha$ is large enough then $\Phi$ is unsatisfiable w.h.p. It is also known that the property of being satisfiable has a sharp threshold [12], and it has been conjectured [5] that this threshold asymptotically occurs at some density $\alpha _k$ . This long been known for $k=2$ [6], but remained an open question for $k\geq 3$ . It was recently shown that this also holds for sufficiently large $k$ [9], and that the threshold density predicted by heuristic methods from statistical physics [19, 20] is correct. For small $k\geq 3$ there are so far only constant separation upper and lower bounds on the possible value of $\alpha _k$ , with [14, 16] giving $\alpha _3 \geq 3.52$ and [10] giving $\alpha _3 \leq 4.506$ . The methods from [19, 20] predict that $\alpha _3=4.26675\ldots$ , but here recent computational work [18] indicates that this value might be too large. The heuristic methods from [19, 20] also predict a highly complex geometry for the set of solutions when $\alpha$ is close to the threshold. Some of these have been confirmed for both other variations of random $k$ -SAT and random colouring problems, see e.g. [7]. The large gap between the bounds for $\alpha _3$ demonstrates that the classical probabilistic methods has so far not been as effective in the analysis of the threshold behaviour for random $k$ -SAT as one would have hoped. As pointed out in [1], part of the reason for this is that the different signs of the variables in the clauses of the formula $\Phi$ leads to problems for the classical second moment method.

With these problems in mind we now introduce the polarised random $k$ -SAT model with polarisation $p$ . In this model a random formula $\Phi$ is generated but now we choose each random clause in the following way. We first pick a $k$ -set $C$ of variables uniformly at random. Next, we flip a fair coin, and if it gives a tail we let each variable in our clause be negated with probability $p$ , independently of each other. Otherwise we negate with probability $1-p$ . For $p=1/2$ this gives the usual random $k$ -SAT model. For the fully polarised case $p=0$ , or 1, we instead get a model were roughly half the clauses contain only negated variables and the other half only pure variables. In the SAT literature a formula of this type is known as a monotone $k$ -SAT formula.

Deciding satisfiability for monotone $k$ -SAT formulae is well known to be NP-complete, this follows from Schaefer’s [23] complexity classification of SAT problems. For $k$ -SAT has long been known [24] that the problem remains NP-complete even if the number of occurrences of each variable is bounded and recently [8] similar restrictions of monotone $k$ -SAT have been shown to remain NP-complete. However, the random version of monotone $k$ -SAT has not been analysed in the existing literature. Now our random model allows us to continuously move between the usual random $k$ -SAT distribution and the distribution for random monotone $k$ -SAT and study how the threshold for satisfiability varies with the polarisation parameter $p$ .

One of the appealing properties of monotone $k$ -SAT is that satisfying assignments can be given a very clean combinatorial description. Given a satisfying assignment for a monotone $k$ -SAT formula $\Phi$ , the set of variables which satisfy the pure clauses is disjoint from the set of variables which satisfy the negative clauses. If we partition $\Phi$ into the two types of clauses as $\Phi =\Phi _1 \cup \Phi _{2}$ , then a solution for $\Phi$ corresponds to two disjoint sets of variables $T_1$ and $T_2$ such that $T_i$ is a transversal for the hypergraph defined by the clauses in $\Phi _i$ . We thus have a description of a satisfying assignment for $\Phi$ in terms of hypergraph properties more closely aligned with the classical machinery of probabilistic combinatorics.

1.2. The Satisfiability threshold for Polarised $\textrm{k}$ -SAT

Just as for random $k$ -SAT we can prove that if the density $\alpha$ is below some constant, then a random polarised $k$ -SAT formula is satisfiable with high probability. Had the clauses all been biased in the same direction (instead of having two types of clauses) we would get the biased $k$ -SAT model studied in [17]. For that model formulas become satisfiable for arbitrarily large densities, as $p$ approaches $0$ . However, for polarised $k$ -SAT the very general results from [11] show that for $\alpha$ above some constant the formula is with high probability not satisfiable, independently of $p$ . As the simulation data in Figure 1 show, the threshold, as given by the curve for 50% chance of satisfiability, depends on $p$ for finite $n$ and becomes flatter for larger $n$ . We will study the asymptotic properties of this threshold curve.

Figure 1. Estimated critical densities of polarised $3$ -SAT for several values of $n$ and $p$ . From top to bottom, the curves are for $n=50$ , $100$ , $150$ , $200$ and $250$ . For $n=300$ and $350$ only simulations with $p=0$ were run; these are the two isolated points on the lower left. The shaded horizontal band is a range of predicted values for $\alpha _3$ , from $4.262$ [18] to $4.26675$ [21].

The main result of this paper is that the probability of satisfiability is asymptotically non-decreasing as $p$ moves away from $\frac{1}{2}$ , which is consistent with what the simulations in Figure 1 suggest. Our approach is to study the effect on satisfiability of adding a single clause to the formula, or switching the sign of one variable in one clause, by connecting them to the number of spine variables of the formula using the Russo-Margulis formula and a lemma from a previous paper by the authors.

We next conjecture that for each fixed $p$ there exists an $\alpha _k(p)$ at which the model has a sharp threshold. The value $\alpha _k(1/2)$ is of course equal to $\alpha _k$ (if they exist), and we prove that $\alpha _k(p)$ is within a constant factor of $\alpha _k(1/2)$ . Furthermore, we conjecture that $\alpha _k(p)=\alpha _k(1/2)$ , and we prove the conjecture in the special case $k=2$ by adapting a classical proof for the threshold value for random $2$ -SAT. If our second conjecture is true we thus have an alternative, and perhaps combinatorially more amenable, route to determining the threshold value for random $k$ -SAT.

1.3. Definitions and notation

We will frequently use asymptotic notation to describe how functions behave as $n\to \infty$ . $O(f), o(f), \omega (f)$ and $\Omega (f)$ will always be considered to be positive quantities, so that we may (for instance) write $f = -O(g)$ to mean that there exists a positive constant $C$ such that $f(n) \geq -Cg(n)$ for all $n\in \mathbb{N}$ . We will also use the notation $f\ll g$ to denote that $f=o(g)$ .

Let $\{x_i\}_{i=1}^n$ be a set of Boolean variables. We will identify TRUE (FALSE) with $+1$ ( $-1$ ). We say that $z$ is a literal on the variable $x$ if $z\,:\!=x$ or $z\,:\!=\neg x$ . A $k$ -clause is an expression of the form $z_1 \vee z_2 \vee \ldots \vee z_k$ , where each $z_j$ is a literal on some variable $x_i$ . We identify $k$ -clauses $C$ with the $k$ -set of literals that define them, so that we can write $z_j\in C$ for the clause above. We say that the variable $x$ occurs in $C$ if $C$ contains a literal on $x$ . For any truth assignment $\sigma \in \{\pm 1\}^n$ , we write $C(\sigma )=1$ if the clause C evaluates to TRUE when $x_i=\sigma _i$ for $i=1,2,\ldots n$ , and we then say that $\sigma$ satisfies C. Otherwise, if $C$ evaluates to FALSE, $C(\sigma )=-1$ .

A $k$ -CNF (short for ‘conjunctive normal form’) is a Boolean formula $F$ of the form $F={C_1\wedge C_2 \wedge \ldots \wedge C_m}$ , where each $C_j$ is a $k$ -clause. For any truth assignment $\sigma$ , we write $F(\sigma )=1$ if $C_1(\sigma )=\ldots = C_m(\sigma )=1$ (i.e. all clauses are satisfied), and $F(\sigma )=-1$ otherwise (i.e. at least one clause is not satisfied). If there exists a $\sigma$ such that $F(\sigma )=1$ , we say that $F$ is satisfiable and write $F\in \textrm{SAT}$ . If no such $\sigma$ exists, we say that $F$ is unsatisfiable and write $F\notin \textrm{SAT}$ .

1.4. The polarised $\textrm{k}$ -SAT model

Given $0\leq p\leq 1$ , we let $\Phi _m =\Phi _m(n,k,p)$ be a $p$ -polarised $k$ -CNF with $m$ clauses on $n$ variables. We will typically use $\Phi$ to denote a $k$ -SAT formula from this distribution, and $F$ to denote any $k$ -SAT formula which is not directly taken from this distribution.

It will be convenient later to be able to separate the randomness that depends on $p$ from the randomness that does not. It will also be useful to couple these formulae so that $\Phi _{m-1}$ is a sub-formula of $\Phi _m$ . With this in mind, we give the following more precise definition of how $\Phi _1, \Phi _2,\ldots$ are constructed.

1. 1. Let $K_1,K_2,\ldots$ be a sequence of $k$ -tuples $(v_1,\ldots, v_k)$ of indices in $\{1,2,\ldots, n\}$ , chosen independently and uniformly at random (without replacement).

2. 2. Let $B_1, B_2,\ldots$ be a sequence of i.i.d. random variables such that ${{\mathbb{P}}(B_i=-1)}={}{{\mathbb{P}}(B_i=1)}=\frac{1}{2}$ .

3. 3. For each $j=1,2,\ldots, k$ , let $P_{1j},P_{2j},\ldots$ be a sequence of i.i.d. random variables such that ${\mathbb{P}}(P_{ij}=1)=p$ and ${\mathbb{P}}(P_{ij}=-1)=1-p$ .

4. 4. For each $k$ -tuple $K_i = (v_1,\ldots, v_k)$ and each $j\leq k$ , let the literal $z_j$ be defined as $x_{v_j}$ if $B_i P_{ij}=1$ and $\neg x_{v_j}$ otherwise. Then let $C_i \,:\!= z_1\vee z_2\vee \ldots \vee z_k$ .

5. 5. For all $m\in \mathbb{N}$ , let $\Phi _m\,:\!=C_1\wedge C_2 \wedge \ldots \wedge C_m$

When $p=0$ or $p=1$ we say that the formula $\Phi _m$ is fully polarised. Replacing $p$ with $1-p$ yields the same probability distribution, so we will henceforth assume (without loss of generality) that $p\leq \frac{1}{2}$ . Note also that although the signs that the variables occur with in a clause are positively correlated ¹ for $p\neq \frac{1}{2}$ , a given variable in a given clause occurs either pure or negated each with probability $\frac{1}{2}$ .

Let $\alpha _k(p,n)\,:\!= \min \big\{m/n\,:\,{\mathbb{P}}(\Phi _{m}\in \textrm{SAT}) \leq \frac{1}{2}\big\}$ be the median satisfiability threshold. For $p=\frac{1}{2}$ we recover the classical random $k$ -SAT problem, and we write $\alpha _k(n)\,:\!= \alpha _k\big(\frac{1}{2},n\big)$ . We say that $\Phi _m$ has a sharp satisfiability threshold if for every $\varepsilon \gt 0$ , the formula $\Phi _m$ is satisfiable w.h.p. whenever $m\lt (\alpha _k(p,n)\!-\!\varepsilon )\cdot n$ and unsatisfiable w.h.p. whenever $m\gt (\alpha _k(p,n)\!+\!\varepsilon )\cdot n$ .

1.5. Results and conjectures

The two main questions that we will concern ourselves with is the location of the satisfiability threshold (as a function of $p$ or $n$ ), as well as its sharpness. Our main result is the following theorem, which lower bounds the threshold of the polarised random $k$ -SAT model in terms of the classical random $k$ -SAT model.

Theorem 1. Let $k\geq 2$ be fixed.

1. 1. For $0\leq p \leq \frac{1}{2}$ the probability of satisfiability is asymptotically non-increasing as a function of $p$ . More precisely, for any $0\leq p \leq q\leq \frac{1}{2}$ ,

   (1) \begin{equation}{\mathbb{P}}(\Phi _m(n,k,p)\in {SAT})\geq{\mathbb{P}}(\Phi _m(n,k,q)\in {SAT})-o(1). \end{equation}

2. 2. For any $0\leq p \leq \frac{1}{2}$ , the satisfiability threshold $\alpha _k(p,n)$ is bounded by

   (2) \begin{equation} \alpha _k(n)-o(1)\leq \alpha _k(p,n) \leq \frac{1+o(1)}{-\log _2\!(1-2^{-k})}. \end{equation}

The first part of this theorem tells us that asymptotically the location of the satisfiability threshold is a decreasing function of $p$ , for $p\leq 1/2$ . In particular for $p=0$ we get the following corollary.

Corollary 2. The value of the satisfiability threshold for random monotone $k$ -SAT is at least as large as that for random $k$ -SAT.

The second part of the theorem tells us that the classical bounds on the location of the threshold for random $k$ -SAT can be generalised to polarised $k$ -SAT as well.

In the special case $k=2$ of the classical random $k$ -SAT model, it is well known that the threshold is sharp and $\alpha _2(n)=1+o(1)$ [5]. Adapting this proof to the polarised model, we have shown that it too has a sharp threshold at this location.

Theorem 3. The polarised $2$ -SAT problem with polarisation $p$ has a sharp satisfiability threshold and $\alpha _2(p,n)=1+o(1)$ . More precisely,

\begin{equation*} {\mathbb {P}}(\Phi _m(n,2,p)\textit { is satisfiable}) = \begin {cases} 1-o(1), &m \lt n-\omega \big(n^{2/3}\big) \\ o(1), &m \gt n+\omega \big((n\ln n)^{9/10}\big), \end {cases} \end{equation*}

In other words, $\alpha _2(p)$ exists and equals $\alpha _2 = 1$ .

It is known that the width of the threshold for classical random $2$ -SAT is $\Theta (n^{2/3})$ [4], so it seems plausible that the lower bound in Theorem 3 is sharp.

The location of the threshold for $k=2$ is asymptotically independent of $p$ , and we conjecture that this holds for larger $k$ as well.

Conjecture 4. For any $0\leq p \leq 1$ and $k\geq 3$ , the threshold of the $p$ -polarised random $k$ -SAT problem asymptotically coincides with the threshold for the classical random $k$ -SAT problem, i.e. $\alpha _k(p,n)=\alpha _k\big(\frac{1}{2},n\big)\pm o(1)$ .

Friedgut [12] proved a general theorem on sharp thresholds, which, as a special case, shows that the classical random $k$ -SAT problem has a sharp threshold. Unfortunately, this theorem is not directly applicable to polarised $k$ -SAT with $p\neq \frac{1}{2}$ , because introducing a polarisation breaks some of the symmetry of classical random $k$ -SAT. ²

Conjecture 5 (Generalised satisfiability conjecture). Given $0\leq p \leq 1$ and $k\geq 3$ , there exists an $\alpha _k(p)$ such that for any $\varepsilon \gt 0$ ,

\begin{equation*}{\mathbb {P}}(\Phi _m(n,k,p)\in \textrm {SAT})=\begin {cases}1-o(1), &m\leq (\alpha _k(p)-\varepsilon )n \\ o(1), &m\geq (\alpha _k(p)+\varepsilon )n.\end {cases}\end{equation*}

If Conjecture 5 is true, then $\alpha _k(p)=\lim _{n\to \infty }\alpha _k(p,n)$ exists. If Conjecture 4 is also true, then $\alpha _k(p)=\alpha _k\big(\frac{1}{2}\big)$ .

Finally, let us note that polarised random $k$ -SAT provides a continuous interpolation between random $k$ -SAT and random monotone $k$ -SAT and our results and conjectures indicate that some properties of the satisfiability threshold do not change during this deformation. Our proof for the first part of Theorem 1 depends on the structure of typical satisfying assignments for a formula, so it would be interesting to see how existing results on the structure of the space of such assignments, of the type in e.g. [3], can be adapted to the polarised model. Similarly it would be interesting to develop a deterministic version of our deformation which could unify complexity results, like those from [24] and [8], for $k$ -SAT and monotone $k$ -SAT.

2. Proof of Theorem 1

It will be convenient to work with the parametrisation $p=\frac{1}{2}-b$ , where $0\leq b\leq \frac{1}{2}$ . Let $P_{m}(b) \,:\!={\mathbb{P}}(\Phi _m\in \textrm{SAT})$ , where $\Phi _m=\Phi _m\big(n,k,\frac{1}{2}-b\big)$ . Theorem 1 will follow from the following proposition.

Proposition 6. For any $k\geq 2$ there exists a $c=c(k)\gt 0$ such that if $n\gt c$ , $m/n\in [2^{-1},2^k]$ , and $b\in \big[0,\frac{1}{2}\big]$ , then $P^{\prime}_{m}(b)\leq cn^{-\frac{k-1}{2k}}$ .

Note that $P^{\prime}_m$ might well be negative, and we have proven no lower bound. If one could show that $P^{\prime}_m\geq -o(1)$ , this would imply Conjecture 4.

2.1. Spine variables and the Russo-Margulis formula

Before we can begin with the proof of Proposition 6, we will need some additional tools. First, the spine variables of a random constraint satisfaction problem were introduced by Boettcher, Istrate & Percus [15] to study the computational complexity of certain algorithms. The main idea of the proof of Proposition 6 is to use spine variables in a slightly different way: A lemma from a previous paper [17] by the authors uses spine variables to characterise when a satisfiable formula can be made unsatisfiable by adding a single clause. We then combine this with using the Russo-Margulis formula to study the effect on satisfiability of changing the sign of a single literal, which leads to a bound on the derivative $P_m^{\prime}$ .

Spine variables were defined in [15] for both satisfiable and unsatisfiable formulae, but we will only the need the definition in the former case.

Definition 7. Let $F$ be a satisfiable formula and $x$ a variable in it. We say that $x$ is a spine variable in $F$ if $x$ has the same value in any assignment satisfying $F$ . If such an $x$ always has value ‘TRUE’, we say that it is a positive spine variable and that it is locked to TRUE. (Similarly for negative.)

Lemma 8 (From [17]). Let $F$ be a satisfiable $k$ -CNF with a set $S_+\subseteq [n]$ of positive spine variables and a set $S_-\subseteq [n]$ of negative spine variables. Then $F\wedge C$ is unsatisfiable if and only if $C$ can be written as

\begin{equation*} C(x) = \Bigg (\bigvee _{i\in K_-} x_i \Bigg )\vee \Bigg (\bigvee _{i\in K_+} \neg x_i\Bigg ) \end{equation*}

for some $K_\pm \subseteq S_\pm$ .

In other words, $F\wedge C$ is unsatisfiable if and only if every variable in the clause $C$ is a spine variable in $F$ , and its sign contradicts the value that that variable is locked to in $F$ .

Next, the Russo-Margulis formula [22] is a theorem from percolation theory. It is usually stated for indicator random variables of monotone events, but we will use a slightly more general version from [13].

Theorem 9 (Russo-Margulis, finite-dimensional case). Let $I$ be a finite set, let the probability space $\mathcal{S}=\{-1,1\}^I$ be equipped with the product measure ${\mathbb{P}}_p$ such that if $s=\{s_i\}_{i\in I}\in \mathcal{S}$ is picked according to ${\mathbb{P}}_p$ , then ${\mathbb{P}}_p(s_i=-1)=p$ for any $i \in I$ . For any $s\in \mathcal{S}$ and $i\in I$ , let $s^{\pm i}$ be $s$ but with the $i$ :th coordinate set to $\pm 1$ . For any real random variable $X(s)$ on $\mathcal{S}$ , let the pivotal $\delta ^{i}X$ be defined by

\begin{equation*} \delta ^{i}X(s)\,:\!= X(s^{+i})-X(s^{-i}). \end{equation*}

Then, for any $0\lt p\lt 1$ ,

\begin{equation*} \frac {\partial }{\partial p} \mathbb {E}_p[X] = \sum _{i\in I} \mathbb {E}_p[\delta ^{i}X]. \end{equation*}

Remark 10. We could have stated this result in terms of conditional expectations without defining $s^{\pm i}$ by instead writing $\mathbb{E}_p[\delta ^i X]$ as $ \mathbb{E}_p[X|s_i=1]-\mathbb{E}_p[X|s_i=-1]$ , but the definition above is more practical since it allows $X(s^{\pm i})$ , $\delta ^i X$ , $\delta ^j X$ etc. to all live on the same probability space.

2.2. Proof of Proposition 6

The proof consists of three inequalities, and chaining these inequalities together gives the desired result. First, we will employ the Russo-Margulis formula with $X\,:\!=\mathbf{1}_{\Phi _m\in \textrm{SAT}}$ to upper bound $P^{\prime}_{m}$ .

Lemma 11. Let $S$ be the (random) number of spine variables of the formula $\Phi _{m-1}$ , and let $M\,:\!=\mathbb{E}[S^k|\Phi _{m-1}\in \textrm{SAT}]$ . Then for all large $n$ and any $b\in \big[0,\frac{1}{2}\big]$ , $P_m^{\prime}(b) \leq 2k^3 P_{m-1}(b) mn^{-k} M^{\frac{k-1}{k}}$ .

Then, we will use a similar argument to lower bound the difference $|P_m-P_{m-1}|$ , again in terms of $M$ .

Lemma 12. There is a constant $c_1=c_1(k)$ such that for any $b\in \big[0,\frac{1}{2}\big]$ and $n\gt c_1$ , $M \leq c_1 n^{k} \cdot |P_m-P_{m-1}|/P_{m-1}+c_1$ .

The third inequality, which upper bounds $|P_m-P_{m-1}|$ , is a result due to Wilson [25]. They proved a lower bound on the width of the phase transition for a family of random constraint satisfaction problems, including $k$ -SAT. Crucially, this bound does not depend on the signs of variables in the random $k$ -SAT formula, but only on its induced hypergraph structure. The following proposition is a corollary of [25, Theorem 1], see their Corollary 4 for more details. We are using their result as it is stated in the last inequality of the proof of their Theorem 1. ³

Theorem 13 (Wilson [25]). Assume that there exist $\alpha, \alpha ^{\prime},\beta,N$ such that for all $n\gt N$ and $b\in \big[0,\frac{1}{2}\big]$ , the formula $\Phi _m\big(n,k,\frac{1}{2}-b\big)$ is satisfiable with probability at least $ 1-\beta n^{-1}$ if $m\lt \alpha n$ , and satisfiable with probability at most $ \beta n^{-1}$ if $m\gt \alpha ^{\prime} n$ .

Then there exists a constant $c_2\gt 0$ such that for all $n\gt c_2$ , all $m_1, m_2$ such that $\alpha \lt m_i/n \lt \alpha ^{\prime}$ , and all $b\in \big[0,\frac{1}{2}\big]$ ,

\begin{equation*} |P_{m_1}(b)-P_{m_2}(b)|\leq \frac {c_2 \cdot |m_1-m_2|}{\sqrt {n}}, \end{equation*}

We will also need some rough bounds on the location of the satisfiability threshold.

Lemma 14. For any $k\geq 2$ , there exist constants $C,c\gt 1$ such that for any $n\gt C$ , $p\in [0,1]$ , and $t\gt 0$ ,

\begin{equation*} {\mathbb {P}}(\Phi _m(n,k,p)\in {\textrm{SAT}}) = \begin {cases} \geq 1-30n^2/{t^3}, &m\lt n-t \\ \leq Cc^{-t}, &m\gt \frac {n}{-\log _2\!(1-2^{-k})}+t. \end {cases} \end{equation*}

In particular, $1-o(1)\leq \alpha _k(p,n) \leq \frac{1}{-\log _2(1-2^{-k})}+o(1)$ , with the $o(1)$ -terms going to $0$ (as $n\to \infty$ ) uniformly in $p$ .

The proofs of Lemmas 11, 12 and 14 are postponed to Section 2.3.

Proof of Proposition 6. We will apply Theorem 13 with $m_1=m$ , $m_2=m-1$ . By Lemma 14, the assumptions of this theorem are satisfied with $\alpha =2^{-1},\alpha ^{\prime}=2^{k}$ and some large $\beta =\beta (k),N=N(k)$ . Combining this bound with Lemma 12, we get

\begin{equation*} M \leq c_1 c_2 n^{k-\frac {1}{2}}/P_{m-1}+c_1 \end{equation*}

The first term on the right-hand side is at least $c_1c_2 n^{k-\frac{1}{2}}\gg 1$ , while the second is $O(1)$ . So the first term dominates, and there must be some constant $c_3=c_3(k)$ such that $M\leq c_3 n^{k-\frac{1}{2}}/P_{m-1}$ . Plugging this bound on $M$ into Lemma 11 yields

\begin{equation*} P^{\prime}_m(b)\leq 2k^3 P_{m-1}^{1/k} \cdot \frac {m}{n^k}\cdot \Big(c_3 n^{k-\frac {1}{2}}\Big)^\frac {k-1}{k}. \end{equation*}

Since $m\lt 2^k n$ by assumption and $P_{m-1}^{1/k}\leq 1$ , the right-hand side is $O\big(n^{-\frac{k-1}{2k}}\big)$ , uniformly in $b$ .

Proof of Theorem 1. If $m/n\in [2^{-1},2^k]$ , then by Proposition 6 there exists a $c\gt 0$ such that

\begin{equation*} P_m\Big (\frac {1}{2}-p\Big )-P_m\Big (\frac {1}{2}-q\Big )=\int _{\frac {1}{2}-q}^{\frac {1}{2}-p} P^{\prime}_m(b)db \leq (q-p)cn^{-\frac {k-1}{2k}} = o(1). \end{equation*}

If $m/n$ is not in this interval, then by Lemma 14 the two terms on the left-hand side (LHS) above are either both $o(1)$ or both $1-o(1)$ , and hence their difference is at most $o(1)$ . In either case, the inequality (1) follows.

For the lower bound in inequality (2), let $m=m(n)$ be the largest integer such that $P_{m}(\frac{1}{2})\geq 0.6$ . Then $P_{m+1}(\frac{1}{2})\leq 0.6$ . By Theorem 13, $|P_{m}(\frac{1}{2})-P_{m+1}(\frac{1}{2})|=o(1)$ , so $P_m(\frac{1}{2})=0.6+o(1)$ . Since classical $k$ -SAT has a sharp satisfiability threshold property (Friedgut [12]), and $P_m(\frac{1}{2})$ is bounded away from both $0$ and $1$ (i.e. $m$ is in the critical window), $m/n=\alpha _k(n)-o(1)$ . By the previous inequality, $P_m(\frac{1}{2}-p)\geq P_m(\frac{1}{2})-o(1)$ , which is at least $0.6-o(1)\gt 0.5$ by assumption. Hence $\alpha _k(p,n)\geq m/n=\alpha _k(n)-o(1)$ . The upper bound in inequality (2) follows directly from Lemma 14.

2.3. Proofs of lemmas

The following simple inequality will be useful to us several times.

Claim 15. If we pick $k$ elements from a set of $s$ elements uniformly at random with replacement, the probability that we pick $k$ distinct elements is at least $(1-k/s)^k\geq 1-k^2/s$ .

Proof. The probability that we pick distinct elements is $\prod _{i=0}^{k-1}(1-i/s)\geq (1-k/s)^k$ , and $(1-k/s)^k\geq 1-k^2/s$ follows from the convexity of $x\mapsto (1-x)^k$ for $x\leq 1$ .

Proof of Lemma 11. To apply the Russo-Margulis formula, we must figure out what the correct pivotals are. Recall that we constructed the random $k$ -CNF $\Phi _m$ from the random variables $K_i$ , $B_i$ and $P_{ij}$ ( $1\leq i\leq m, 1\leq j\leq k$ ), where $K_i$ is the ordered list of variables occurring in the $i$ th clause $C_i$ , and $B_i \cdot P_{ij}$ is the sign of the $j$ :th variable in $C_i$ . Let $H\,:\!=((K_1,B_1),(K_2,B_2),\ldots,(K_m,B_m))$ denote the (signed, ordered) hypergraph structure of the formula $\Phi _m$ . Note that $H$ does not depend on $p$ . We will condition on $H$ , and study the effect on $X$ of switching the value of one of the random variables $P_{ij}$ . This only affects the clause $C_i$ , and leaves the rest of the formula $\Phi _m$ unaffected. It is therefore convenient to decompose $\Phi _m$ as $F_i\wedge C_i$ , where we define the formulae $F_{i}\,:\!=\Phi _m-C_i=\bigwedge _{\ell \neq i, 1\leq \ell \leq m} C_\ell$ . Note that $F_i$ is independent from $P_{ij}$ .

Let $C_i^{+j}$ and $C_i^{-j}$ be the two clauses obtained from $C_i$ by letting the $j$ th variable in $C_i$ occur with sign $B_i$ and $-B_i$ respectively. (Instead of having signs given by $B_iP_{ij}$ , as it has in $C_i$ .) Then (still conditional on $H$ ) the pivotal is given by

\begin{align*} \delta ^{ij}X &= \mathbf{1}_{F_{i}\wedge C_i^{+j} \in \textrm{SAT}} - \mathbf{1}_{F_{i}\wedge C_i^{-j} \in \textrm{SAT}} \\ &= \mathbf{1}_{F_{i}\wedge C_i^{-j} \notin \textrm{SAT}} - \mathbf{1}_{F_{i}\wedge C_i^{+j} \notin \textrm{SAT}}. \end{align*}

Applying the Russo-Margulis formula to the product space $\{\pm 1\}^I$ with index set $I\,:\!=\{1,\ldots, m\}\times \{1,\ldots, k\}$ and with product measure ${\mathbb{P}}_p(\bullet ) \,:\!={\mathbb{P}}(\bullet |H)$ leads to

\begin{equation*} \frac {d}{dp}{\mathbb {P}}(\Phi _m\in \textrm {SAT}|H) =\sum _{i=1}^m \sum _{j=1}^k \mathbb {E}[ \delta ^{ij}X|H]. \end{equation*}

Taking expectations over $H$ of both sides gives us

\begin{equation*} \mathbb {E}\left [\frac {d}{dp}{\mathbb {P}}(\Phi _m\in \textrm {SAT}|H) \right ]=\sum _{i=1}^m \sum _{j=1}^k \mathbb {E}[ \delta ^{ij}X], \end{equation*}

and since there are only finitely many possible (signed, ordered) hypergraphs $H$ on $n$ vertices, we can exchange the order of expectation and differentiation in the LHS. In the sum on the right-hand side all terms are equal, and thus

\begin{equation*} -\frac {dP_m}{db}=\frac {dP_m}{dp} =mk\mathbb {E}[ \delta ^{m1}X], \end{equation*}

since $p=\frac{1}{2}-b$ . Our objective is now to bound $\mathbb{E}[ \delta ^{m1}X]$ . The formula $F_m=\Phi _{m-1}$ will be used frequently throughout the rest of this proof, so for the sake of convenience we drop the subscripts and let $\Phi \,:\!=F_m=\Phi _{m-1}$ .

Let $S$ be the number of spine variables of $\Phi$ if this formula is satisfiable (and not defined otherwise). We will now lower bound $\mathbb{E}[\delta ^{m1}X]$ in terms of $M\,:\!={\mathbb{E}[S^k|\Phi \in \textrm{SAT}]}$ . Note that the pivotal $\delta ^{m1}X$ is non-zero iff exactly one of $\Phi \wedge C_m^{+1}$ and $\Phi \wedge C_m^{-1}$ is satisfiable. That only happens if (i) $\Phi$ is satisfiable and (ii) every variable in $C_m$ is one of the $S$ spine variables of $\Phi$ . Since $\Phi =\Phi _{m-1}$ is satisfiable with probability $P_{m-1}$ ,

\begin{equation*} \mathbb {E}[ \delta ^{m1}X] = P_{m-1}\mathbb {E}[ \delta ^{m1}X|\Phi \in \textrm {SAT}]. \end{equation*}

Let $S_+$ ( $S_-$ ) be the set of positive (negative) spine variables (so that $|S_+|+|S_-|=S$ ), and let $\Gamma$ be the event $\{(i), (ii), |S_+|=s_+, |S_-|=s_-\}$ for some $s_\pm$ . Conditional on $\Gamma$ , the variables of $C_m$ form a $k$ -tuple $K_m$ of variables, chosen uniformly at random from the $s\,:\!=s_++s_-$ spine variables without replacement. If $s$ is large compared to $k$ , this $k$ -tuple will typically be the same as a sample taken with replacements.

We therefore let $\tilde K=(v_1,\ldots, v_k)$ be a random $k$ -tuple chosen uniformly at random from $\{1, \ldots,n\}$ with replacement, and couple it to $K_m$ such that every element in $\tilde K$ is also in $K_m$ . ⁴ Then $\tilde K=K_m$ whenever $\tilde K$ consists of $k$ distinct elements, which by Claim 15 happens with probability at least $1-k^2/s$ (conditional on $\Gamma$ ).

For the sake of convenience, we will for any clause $C=z_1\vee z_2 \vee \ldots \vee z_k$ define the clause $-C$ as $-C\,:\!=\neg z_1\vee \neg z_2 \vee \ldots \vee \neg z_k$ .

Let $z_j$ be the literal $x_{v_j}$ if $P_{mj}=1$ and $\neg x_{v_j}$ otherwise, and let the clauses $D_\pm$ be defined as $D_+\,:\!= x_{v_1}\vee z_2\vee \ldots z_k$ and $D_-\,:\!= \neg x_{v_1}\vee z_2\vee \ldots z_k$ . Let $C_+\,:\!=D_+$ if $B_m=1$ , and $C_+\,:\!=-D_+$ otherwise, and analogously for $C_-$ . Then $C_+=C_m^{+1}$ and $C_-=C_m^{-1}$ with probability at least $1-k^2/s$ , independently of $\Phi$ , so we can approximate $\mathbb{E}[\delta ^{m1}X|\Gamma ]$ with $\mathbb{E}[\mathbf{1}_{\Phi \wedge C_- \notin \textrm{SAT}} - \mathbf{1}_{\Phi \wedge C_+ \notin \textrm{SAT}}|\Gamma ]$ . We will first show that the latter expected value is $\geq 0$ , and then bound the error in the approximation.

Claim 16. Let $\tilde X\,:\!=\mathbf{1}_{\Phi \wedge C_- \notin \textrm{SAT}} - \mathbf{1}_{\Phi \wedge C_+ \notin \textrm{SAT}}$ . Then $\mathbb{E}[\tilde X|\Gamma ] \geq 0$ .

Proof of claim. Let $a$ be the number such that $\frac{1}{2}+ a = \frac{s_+}{s}$ , i.e. the fraction of positive spine variables. Each literal $z_2,\ldots z_k$ is pure with probability $\frac{1}{2}-b$ and negated otherwise, while (conditional on $\Gamma$ ) each corresponding variable is a positive spine variable with probability $\frac{1}{2}+a$ . Hence the conditional probability that all of them disagree with the spine is

\begin{equation*} \left (\Big (\frac {1}{2}-a\Big )\Big (\frac {1}{2}-b\Big )+\Big (\frac {1}{2}+a\Big )\Big (\frac {1}{2}+b\Big )\right )^{k-1}\!\! = \Big (\frac {1}{2}+2ab\Big )^{k-1}. \end{equation*}

The first literal of $D_+$ is $x_{v_1}$ , and thus disagree with the spine with probability $\frac{1}{2}-a$ . So, conditional on $\Gamma$ , the probability that $\Phi \wedge D_+$ is unsatisfiable is $\big (\frac{1}{2}-a\big )\cdot \big (\frac{1}{2}+2ab\big )^{k-1}$ . Similarly, the first literal of $D_-$ is $\neg x_{v_1}$ , which disagrees with the spine with probability $\frac{1}{2}+a$ , so $\Phi \wedge D_-$ is unsatisfiable with probability ${\big (\frac{1}{2}+a\big )}\cdot{ \big (\frac{1}{2}+2ab\big )^{k-1}}$ . Together, these observations give us that

(3) \begin{align} &{\mathbb{P}}(\Phi \wedge D_-\notin \textrm{SAT}|\Gamma )-{\mathbb{P}}(\Phi \wedge D_+\notin \textrm{SAT}|\Gamma ) \nonumber \\ & \quad= \left (\Big (\frac{1}{2}\!+\!a\Big )-\Big (\frac{1}{2}\!-\!a\Big )\right )\cdot \Big (\frac{1}{2}+2ab\Big )^{k-1}= 2a\cdot \Big (\frac{1}{2}+2ab\Big )^{k-1}. \end{align}

If we consider $-D_+$ and $-D_-$ , an analogous argument gives that

(4) \begin{align} {\mathbb{P}}(\Phi \wedge -D_-\notin \textrm{SAT}|\Gamma )-{\mathbb{P}}(\Phi \wedge -D_+\notin \textrm{SAT}|\Gamma ) &= -2a\cdot \Big (\frac{1}{2}-2ab\Big )^{k-1}. \end{align}

Since $C_\pm$ is equally likely to be $D_\pm$ as $-D_\pm$ , averaging gives

\begin{align*} \mathbb{E}[\tilde X|\Gamma ] &={\mathbb{P}}(\Phi \wedge C_-\notin \textrm{SAT}|\Gamma )-{\mathbb{P}}(\Phi \wedge C_+\notin \textrm{SAT}|\Gamma ) =\frac{1}{2}\big [(3)+(4)\big ] \\ &=a\cdot \underbrace{\bigg (\Big (\frac{1}{2}+2ab\Big )^{k-1}-\Big (\frac{1}{2}-2ab\Big )^{k-1}\bigg )}_{=:\,f(a,b)}. \end{align*}

If $a\!=\!0$ or $b\!=\!0$ , then $f(a,b)=0$ and hence $\mathbb{E}[\tilde X|\Gamma ]=0$ . Otherwise, if $b\gt 0$ and $a\neq 0$ , then $a$ and $f(a,b)$ have the same sign, and their product is positive.

But as we noted earlier, this is not quite the expected value of the pivotal $\delta ^{m1}X$ . The probability that the $k$ -tuple $\tilde K$ (drawn with replacement) equals $K_m$ (drawn without replacement) is at least $1-k^2/s$ by Claim 15. But then $\delta ^{m1}X=\tilde X$ with probability at least $1-k^2/s$ (independently of $\Gamma$ ), and since $|\delta ^{m1}X-\tilde X|\leq 2$ ,

\begin{equation*} \mathbb {E}\big [ \delta ^{m1}X\big | \Gamma \big ] \,\geq \, \mathbb {E}[\tilde X|\Gamma ] -2{\mathbb {P}}\big ( \delta ^{m1}X\neq \tilde X\big |\Gamma \big ) \,\geq \, -\frac {2k^2}{s}. \end{equation*}

Recall that $\Gamma = \{\Phi \in \textrm{SAT}, \textrm{all variables in $C$ are spines}, |S_+|=s_+, |S_-|=s_-\}$ . The probability that all variables in $C$ are spine variables in $\Phi$ is $\binom{s}{k}/\binom{n}{k}\leq (s/n)^k$ , and if some variable is not, then $\delta ^{m1}X=0$ . Thus

\begin{equation*} \mathbb {E}\Big [ \delta ^{m1}X\Big | \Phi \in \textrm {SAT},|S_+| = s_+,|S_-| = s_-\Big ] = \frac {\binom {s}{k}}{\binom {n}{k}}\cdot \mathbb {E}\Big [ \delta ^{m1}X\Big | \Gamma \Big ] \geq -\left (\frac {s}{n}\right )^k \cdot \frac {2k^2}{s}. \end{equation*}

The conditional expectation $\mathbb{E}\big [ \delta ^{m1}X\big | \Phi \in \textrm{SAT}, S=s\big ]$ is a weighted average, over all $s_\pm$ with $s_++s_-=s$ , of the LHS above. Since each such term is at least $-2s^{k-1} k^2/n^{k}$ , their weighted average is also at least this large. By taking expectation over $S$ , we find that

\begin{equation*} {\mathbb {E}[ \delta ^{m1}X| \Phi \in \textrm {SAT}] } \geq - \frac {2k^2}{n^k}\cdot \mathbb {E}[S^{k-1}|\Phi \in \textrm {SAT}]. \end{equation*}

Our aim is to bound $P_{m}^{\prime}(b)$ in terms of $M\,:\!=\mathbb{E}\big[S^k\big|\Phi \in \textrm{SAT}\big]$ . By Jensen’s inequality and the convexity of $z\mapsto z^{\frac{k}{k-1}}$ ,

\begin{equation*}\mathbb {E}[S^{k-1}|\Phi \in \textrm {SAT}]\leq (\mathbb {E}[S^{k}|\Phi \in \textrm {SAT}])^\frac {k-1}{k}=M^{\frac {k-1}{k}},\end{equation*}

and plugging that into the previous inequality leads to

\begin{equation*} \mathbb {E}[ \delta ^{m1}X| \Phi \in \textrm {SAT}] \geq -\frac {2k^2}{n^k}M^{\frac {k-1}{k}}. \end{equation*}

Recalling that $\frac{dP_m}{dp} = mk\mathbb{E}[ \delta ^{m1}X]$ and $\mathbb{E}[ \delta ^{m1}X] = P_{m-1}\mathbb{E}[ \delta ^{m1}X|\Phi \in \textrm{SAT}]$ ,

\begin{equation*} \frac {dP_m}{dp} \geq -P_{m-1} \frac {2mk^3}{n^k}M^{\frac {k-1}{k}}. \end{equation*}

Recalling also that $\frac{dP_m}{dp}=-\frac{dP_m}{db}$ (since $p=\frac{1}{2}-b$ ) gives the desired result.

Proof of Lemma 12. The difference $P_{m-1}-P_{m}$ is the probability of the event $A\,:\!=\{\Phi _m\notin \textrm{SAT}, \Phi _{m-1}\in \textrm{SAT}\}$ . Since we want to lower bound this, let $B\,:\!=\{C_m \textrm{ has same sign on all variables}\}$ and consider the probability of $A\cap B$ .

Conditional on $\{\Phi _{m-1}=F\}$ for some satisfiable formula $F$ , by Lemma 8 the event $A \cap B$ occurs iff the $k$ variables in $C_m$ are either all negated and among the $s_+$ positive spine variables, or all pure and among the $s_-$ negative spine variables. The probability of this is

\begin{equation*} \frac {\binom {s_+}{k}+\binom {s_-}{k}}{\binom {n}{k}}\cdot \frac {p^k+(1-p)^k}{2}. \end{equation*}

Since the function $p\mapsto p^k$ is convex on $[0,1]$ , the second factor is at least $2^{-k}$ . Note also that $t\mapsto \binom{t}{k}$ is a convex function on the non-negative integers, and hence the first factor is at least $f(s)\,:\!=2\binom{s/2}{k}/\binom{n}{k}$ , where $s\,:\!=s_++s_-$ . The standard bounds $(t/ek)^k\leq \binom{t}{k}\leq (t/k)^k$ are valid for $t\geq k$ , so for $s\geq 2k$ we have that $f(s)\geq 2(s/2en)^{k}$ . If instead $s\lt 2k$ , $f(s)\geq 0 \gt \lambda \cdot (s^k-(2k)^k)$ for any $\lambda \gt 0$ . In either case,

\begin{equation*} {f(s)\,\geq \, 2(2en)^{-k}\cdot \big (s^k-(2k)^{k}\big )}. \end{equation*}

Then, by taking expectation over satisfiable $\Phi _{m-1}$ (and hence over $S$ ),

\begin{align*}{\mathbb{P}}(A\cap B|\Phi _{m-1}\in \textrm{SAT}) &\geq \mathbb{E}[2^{-k}f(S) |\Phi _{m-1}\in \textrm{SAT}] \\ &\geq 2(4en)^{-k}\cdot \left (\mathbb{E}[S^k |\Phi _{m-1}\in \textrm{SAT}]-(2k)^k\right ) . \end{align*}

Noting that the LHS is at most ${\mathbb{P}}(A|\Phi _{m-1}\in \textrm{SAT}) = (P_{m-1}-P_m)/P_{m-1}$ and solving for $M=\mathbb{E}[S^k\big |\Phi _{m-1}\in \textrm{SAT}]$ gives the desired inequality.

Proof of Lemma 14. The first inequality is an easy corollary of Proposition 21: Given $\Phi \,:\!=\Phi _m(n,k,p)$ , $k\geq 3$ , uniformly at random remove all but $2$ literals from each clause to get a $2$ -SAT formula $\Phi ^{\prime}$ . Any satisfying assignment to $\Phi ^{\prime}$ is also a satisfying assignment to $\Phi$ , and $\Phi ^{\prime}$ is a $p$ -polarised $2$ -SAT formula. Hence ${\mathbb{P}}(\Phi _m(n,k,p)\in \textrm{SAT}) \geq{\mathbb{P}}(\Phi _m(n,2,p)\in \textrm{SAT})$ , and by Proposition 21 this probability is at least $1-30/(n\varepsilon ^3)$ for $m\lt (1-\varepsilon ) n$ . For the second inequality we will upper bound the expected number of satisfying assignments.

Claim 17. Let $q_i\,:\!={\mathbb{P}}(C(\sigma )=-1)$ be the probability that a $\sigma \in \{\pm 1\}^n$ with $i$ coordinates set to ‘TRUE’ does not satisfy a random $p$ -polarised $k$ -clause $C$ . Then $q_i \geq 2^{-k}-k^2/n$ .

Proof of claim. Let $K,\tilde K$ be random $k$ -tuples $(v_1,\ldots v_k)$ and $(\tilde v_1,\ldots \tilde v_k),$ chosen uniformly at random from the set $\{1\,\ldots,n\}$ , without and with replacement respectively. By Claim 15, we can couple $K,\tilde K$ such that they are equal with probability at least $1-k^2/n$ . Like in Section 1.4, let the random variable $B$ equal $\pm 1$ with probability $\frac{1}{2}$ , and $P_j=1$ with probability $p$ (and $-1$ otherwise). Let $z_j \,:\!= x_{v_j}$ and $\tilde z_j\,:\!= x_{\tilde v_j}$ if $BP_j=1$ , but $z_j \,:\!= \neg x_{v_j}$ and $\tilde z_j \,:\!= \neg x_{\tilde v_j}$ otherwise. Finally, let $C\,:\!=z_1\vee \ldots \vee z_k$ and $\tilde C\,:\!=\tilde z_1\vee \ldots \vee \tilde z_k$ be $k$ -clauses.

Conditional on $B=1$ , the events $\{\tilde z_j(\sigma )=-1\}_{j=1}^k$ are independent and each occur with the same probability $\rho (\sigma )$ . Conditional on $B=-1$ , they also occur independently, but with probability $1-\rho$ . Hence the probability that $\sigma$ does not satisfy $\tilde C$ is $\frac{1}{2}(\rho ^k+(1-\rho )^k) \geq 2^{-k}$ . But $C=\tilde C$ with probability at least $1-k^2/n$ , so the probability that $\sigma$ does not satisfy $C$ is at least $2^{-k}-k^2/n$ .

Let $m\gt -n/\log _2\!(1-2^{-k})+t$ . The logarithm of the expected number of satisfying assignments to $\Phi _m(n,k,p)$ is then equal to

\begin{align*} \log _2\left (\sum _{i=1}^n\binom{n}{i}(1-q_i)^{m}\right ) \leq \log _2\left (2^n \cdot (1-2^{-k}+k^2/n)^{m}\right ) \\ \leq n \cdot \Big ( \underbrace{1-\frac{\log _2\! (1\!-\!2^{-k}\!+\!k^2/n)}{\log _2\!(1-2^{-k})}}_{(i)}\Big )+ \underbrace{t\log _2(1-2^{-k}+k^2/n)}_{(ii)}. \end{align*}

By doing a first-order Taylor expansion of the increasing and convex function $r\mapsto 1-\log _2\!(1-2^{-k}+r)/\log _2(1-2^{-k})$ at $r=0$ , we see that $(i)\leq 2^k k^2/n$ for large $n$ . The first term above is therefore at most $2^k k^2$ . For $n\gt 2^{k+1} k^2$ , the second term $(ii)$ is at most $t\log _2(1-2^{-k-1})\lt -2^{-k-2} t$ . The second inequality of the proposition follows.

3. Proof of Theorem 3

For the classical $2$ -SAT problem, the threshold value of $c = 1$ was established by Chvátal & Reed [5] by exploiting some of the structure specific to $2$ -SAT. Our proof is fairly similar to theirs, but with some minor complications.

A $2$ -clause is of the form $x\vee y$ , which is logically equivalent the implication $\neg x \Rightarrow y$ , and also to the implication $\neg y \Rightarrow x$ . Thus, a $2$ -SAT formula with $m$ clauses on $n$ variables can be represented by a digraph $G$ with $2m$ arcs on the following $2n$ vertices: $\{x_1,\ldots, x_n, \neg x_1,\ldots, \neg x_n \}$ . We call any directed cycle in G a bicycle ⁵ if it contains both $x_i$ and $\neg x_i$ for some $i$ . It is clear that the formula is unsatisfiable if the digraph contains a bicycle, because from a bicycle the contradiction $x_i\Leftrightarrow \neg x_i$ can be derived. Less obviously, this is an ‘if and only if’-condition.

Lemma 18 (Aspvall, Plass & Tarjan [2]). A $2$ -SAT instance is satisfiable if and only if there is no bicycle in the associated digraph of implications.

We will establish upper and lower bounds on the satisfiability threshold by applying the second and first moment method to certain structures related to bicycles.

Definition 19. A unicycle $($ short for unique bicycle $)$ is an even length bicycle with a unique repeated variable $x$ and with that variable occurring precisely twice, once as $x$ and once as $\neg x$ , at diametrically opposed points along the cycle.

A pretzel is a directed path $\ell \to \ell _1\to \ldots \to \ell _t\to \ell ^{\prime}$ , where each $\ell _i$ is a literal on $z_i$ , the $z_i$ ’s are distinct, and $\ell,\ell ^{\prime}$ are literals on some variables $z,z^{\prime}\in \{z_1, \ldots,z_t\}$ .

A pair of edges is conjugate if the corresponding implications are contrapositives of one another (i.e. both implications arise from the same clause).

Lemma 20. For directed graphs $G$ we have the following.

\begin{equation*}(\exists \textit { unicycle} \in G) \Rightarrow (\exists \textit { bicycle} \in G) \Rightarrow (\exists \textit { pretzel} \in G)\end{equation*}

Proof. The first implication is clear: any unicycle is a bicycle. For the second one, let $C\subseteq G$ be a bicycle. Pick a maximal path $P\subset C$ such that the literals in $P$ are on disjoint variables. We can then write $P$ as $\ell _1 \to \ell _2 \to \ldots \to \ell _t$ for some $t\gt 0$ , where each $\ell _i$ is a literal on a variable $z_i$ , and the $z_i$ ’s are distinct.

Let $\ell,\ell ^{\prime}$ be the unique literals in $C$ such that $\ell \to \ell _1$ and $\ell _t\to \ell ^{\prime}$ , or in other words the immediate predecessor and successor to $P$ . It follows from the maximality of $P$ that $\ell,\ell ^{\prime}$ are literals on some variables in the set $\{z_1,\ldots,z_t\}$ . (If $\ell$ or $\ell ^{\prime}$ were a literal on a variable not in this set, we could extend $P$ to a larger path of literals on disjoint variables.) Hence the path $\ell \to \ell _1 \to \ell _2 \to \ldots \to \ell _t \to \ell ^{\prime}$ is a pretzel.

We will use the first moment method to show that for any $0\leq p \leq 1$ there is no pretzel (w.h.p.) when $m \lt (1-\varepsilon )n$ (and hence there is no bicycle). We will use the second moment method to show that for $p=0$ there is a unicycle (w.h.p.) when $m \gt (1+\varepsilon )n$ (and hence there is a bicycle). Then Proposition 6 will imply that the same is true for every $0\leq p \leq 1$ .

Proposition 21. For any $\varepsilon =\varepsilon (n)$ , if $m\lt (1-\varepsilon )n$ then the probability that there exists a pretzel is at most $30/(n\varepsilon ^3)$ .

Proof. We will begin by upper bounding the expected number of pretzels with $t+1$ edges. Note that no arc in a pretzel is conjugate to another arc in it, so they all correspond to distinct $2$ -clauses. Furthermore, a pair of variables $x_i,x_j$ can occur in at most one $2$ -clause (since we pick such pairs without replacement).

There are at most $n^t$ ways to choose the $t$ variables $z_i$ , and then at most $t^2$ ways to choose $z$ and $z^{\prime}$ from the $t$ -set $\{z_1,\ldots z_t\}$ , so there are at most $n^t t^2$ ways to choose the variables in a pretzel.

The probability that each of the $t+1$ pairs of variables $zz_1, z_1 z_2, \ldots, z_{t-1}z_t, z_t z^{\prime}$ occurs in some $2$ -clause in the $2$ -SAT formula is at most $(m/\binom{n}{2})^{t+1}$ . Conditioned on these $t+1$ pairs occurring as $2$ -clauses, what is the probability that the signs of variables in all of them are such that the corresponding arcs in the digraph form a directed path? In other words, that the $2$ -clauses form implications $\ell \Rightarrow \ell _1\Rightarrow \ldots \Rightarrow \ell _t\Rightarrow \ell ^{\prime}$ , where the $\ell _i$ ’s are literals on the variables $z_i$ .

We reveal the signs of variables in clauses in order: First, condition on the event that $z_1$ occurs pure in the first clause (whose variables are $z$ and $z_1$ ), i.e. $\ell _1=z_1$ so that the clause is $\neg \ell \vee z_1$ , for either $\ell =z$ or $\ell =\neg z$ . This is equivalent to the implication $\ell \Rightarrow z_1$ .

Then, in order for the next clause (with variables $z_1, z_2$ ) to form an implication of the form $z_1 \Rightarrow \bullet$ , the variable $z_1$ must occur negated in it, but the sign of $z_2$ is not constrained. In other words, the second clause must be either $\neg z_1 \vee z_2$ or $\neg z_1 \vee \neg z_2$ . The probability of this event is $\frac{1}{2}$ . But if we instead condition the first clause being $\ell \Rightarrow \neg z_1$ , the probability that the next clause is $\neg z_1\Rightarrow \bullet$ is also $\frac{1}{2}$ .

Similarly, for each subsequent clause (with variables $z_i, z_{i+1}$ ), the sign of $z_i$ in it must be the opposite of the sign that $z_i$ had in the previous clause, which happens with probability $\frac{1}{2}$ independently of previous clauses. The probability that all these $t$ events occur is $\left (\frac{1}{2}\right )^{t}$ . The expected number of pretzels is thus at most

\begin{align*} \mathbb{E}[\#\textrm{ pretzels}]\leq \, &\sum _{t=1}^{2n} n^{t} t^2 \cdot \left ( \frac{m}{\binom{n}{2}}\right )^{t+1}\left (\frac{1}{2}\right )^{t} \\ =\, &\frac{2}{n}\cdot \sum _{t=1}^{2n} t^2 \left (\frac{m}{n-1} \right )^{t+1} \\ \lt \, &\frac{2}{n}\left (\frac{n}{n-1}\right )^{2n}\cdot \sum _{t=1}^{2n} t^2 \Bigg (\frac{m}{n} \Bigg )^{t+1}\!\!\!\!\!\!. \end{align*}

By the assumption on $m$ , $\frac{m}{n}\lt 1-\varepsilon$ . But then the sum above is at most

\begin{equation*}\sum _{t=1}^{\infty } t^2 (1-\varepsilon )^{t+1} = \frac {(1-\varepsilon )^2(2-\varepsilon )}{\varepsilon ^3}\lt \frac {2}{\varepsilon ^3},\end{equation*}

so that the expected number of pretzels is at most

\begin{equation*} \frac {2}{n}\left (\frac {n}{n-1}\right )^{2n}\cdot \frac {2}{\varepsilon ^3} \lt 4e^2 \cdot \frac {1}{n\varepsilon ^3}. \end{equation*}

Hence there exists a pretzel when $m\lt (1-\varepsilon )n$ with probability $\leq 30/(n \varepsilon ^3)$ .

Proposition 22. Let $p=0$ and $\frac{1}{2}\gt \varepsilon \gg n^{-0.1}(\ln n)^{0.9}$ . Then if $m\gt (1+\varepsilon )n$ there exists a unicycle (with high probability).

Proof. By assumption, $(n \ln n)^{0.9}\ll \varepsilon n$ . Let $t=t(n)$ be a sequence of odd integers such that $(n \ln n)^{0.9} \ll t^9\ll \varepsilon n$ . We will consider only unicycles on precisely $2t$ vertices and show that at least one such unicycle is present with high probability.

The unicycles are much more constrained for the fully polarised $2$ -SAT problem than for the classical $2$ -SAT problem. Since clauses of the form $x_i \vee \neg x_j$ occur with probability $0$ , there will be no arcs of the form $x_i \Rightarrow x_j$ or $\neg x_i \Rightarrow \neg x_j$ in the digraph of implications. In other words, the digraph becomes bipartite, with the vertices partitioned into the sets $V_+\,:\!=\{x_1,x_2,\ldots x_n\}$ and $V_-\,:\!=\{\neg x_1,\neg x_2,\ldots \neg x_n\}$ . The proof of Theorem 4 of [5] uses the second moment method applied to the number of unicycles on the complete digraph, and we will describe how to adapt the proof to instead count the number of unicycles on the complete bipartite digraph.

First, note that the total number of possible clauses in the fully polarised model is $2\binom{n}{2}$ , compared to $4\binom{n}{2}$ in the original model. Note also that a path from $x_i$ to $\neg x_i$ has an odd number of edges, so it is necessary that $t$ is odd.

Let $(n)_t$ denote the falling factorial $n(n-1)\ldots (n-t+1)$ . A directed path $\ell _1 \Rightarrow \ldots \Rightarrow \ell _t$ , where each $\ell _i$ is a literal on the variable $z_i$ , is determined by the underlying sequence of variables $z_i$ together with whether $\ell _1=z_1$ or $\ell _1=\neg z_1$ , so there are $2\cdot (n)_{t}$ paths of length $t$ in the complete bipartite digraph. Note that $1\gt (n)_{t}/n^{t}\gt (1-t/n)^t$ , and since $t\ll \sqrt{n}$ by assumption, $2\cdot (n)_{t}=(1+o(1))\cdot 2n^t$ . Similarly, the complete digraph on $2n$ vertices has $(2n)_t=(1+o(1)) \cdot (2n)^t$ paths.

Keeping these differences in mind, the estimates in Theorem 4 of [5], pages 625–626, of the first two moments of the number of unicycles on $2t$ vertices carry through with minimal alterations: Replace all powers of $2n$ with powers of $n$ , every power of $2$ with a power of $1$ , except in estimate $(iii)$ , and replace $4\binom{n}{2}$ with $2\binom{n}{2}$ throughout the proof of said theorem. In the end, all of these alterations cancel out, and we reach the same conclusion that as long both

(5) \begin{equation} t^9/\varepsilon n=o(1), \textrm{ and } \end{equation}

(6) \begin{align} tn (1-\varepsilon )^t/\varepsilon =o(1), \end{align}

then there exists at least one unicycle (w.h.p.) whenever $m\gt (1+\varepsilon )n$ . Condition (5) holds by our choice of $t$ . To show that (6) holds, we deal with ${tn}/{\varepsilon }$ and $(1-\varepsilon )^t$ separately. Note that $\varepsilon t \gg t^{10}/n \gg \ln n$ , so

\begin{equation*} (1-\varepsilon )^t \leq \exp (\!-\!\varepsilon t) = \exp (\!-\!\omega (\ln n))=n^{-\omega (1)}. \end{equation*}

On the other hand, $tn/\varepsilon \lt t^9n/\varepsilon =o(n^2)$ by our choice of $t$ . It follows that $tn (1-\varepsilon )^t/\varepsilon =o(1)$ . Hence both (5) and (6) hold, and the theorem follows.

Proof of Theorem 3. Proposition 21 and Lemma 20 together show that $\Phi _m(n,2,p)$ is satisfiable w.h.p. for any $m\leq n - \omega (n^{2/3})$ . For the upper bound, by Theorem 1:

\begin{equation*}{\mathbb {P}}(\Phi _m(n,2,p) \notin \textrm {SAT}) \geq {\mathbb {P}}(\Phi _m(n,2,0) \notin \textrm {SAT})-o(1).\end{equation*}

Proposition 22 and Lemma 20 together show that $\Phi _m(n,2,0)$ is unsatisfiable w.h.p. for any $m\geq n+\omega ((n \ln n)^{9/10})$ , so the right-hand side above is $1-o(1)$ . In other words, $\Phi _m(n,2,p)$ is unsatisfiable w.h.p.⁶