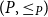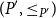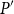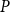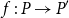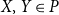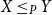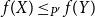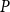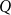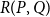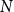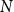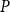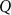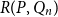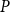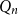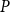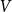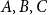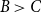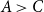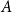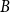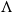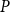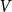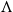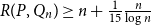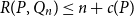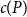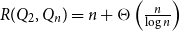1. Introduction
Ramsey-type problems for partially ordered sets, or shortly posets, were considered first in great generality by Nešetřil and Rödl [Reference Nešetřil and Rödl24], who determined all posets
![]() $U$
such that for any poset
$U$
such that for any poset
![]() $P$
there is a ground poset
$P$
there is a ground poset
![]() $W$
with the property that any colouring of induced copies of
$W$
with the property that any colouring of induced copies of
![]() $U$
in
$U$
in
![]() $W$
with a fixed number of colours results in a monochromatic induced copy of
$W$
with a fixed number of colours results in a monochromatic induced copy of
![]() $P$
. See also a paper by Paoli, Trotter, and Walker [Reference Paoli, Trotter and Walker25] on this topic. If
$P$
. See also a paper by Paoli, Trotter, and Walker [Reference Paoli, Trotter and Walker25] on this topic. If
![]() $U$
is the poset consisting of a single element, we arrive at a natural special case, where one writes
$U$
is the poset consisting of a single element, we arrive at a natural special case, where one writes
![]() $W\rightarrow P$
if any two-colouring of the elements of
$W\rightarrow P$
if any two-colouring of the elements of
![]() $W$
contains a monochromatic induced copy of
$W$
contains a monochromatic induced copy of
![]() $P$
. Kierstead and Trotter [Reference Kierstead and Trotter18] considered this setting for general posets with the goal of minimising
$P$
. Kierstead and Trotter [Reference Kierstead and Trotter18] considered this setting for general posets with the goal of minimising
![]() $p(W)$
for all
$p(W)$
for all
![]() $P$
with a fixed
$P$
with a fixed
![]() $p(P)$
, where
$p(P)$
, where
![]() $p$
is a poset parameter such as size, height, or width.
$p$
is a poset parameter such as size, height, or width.
In this paper, we consider a closely related poset Ramsey problem, where the ground poset is a Boolean lattice
![]() $Q_N$
, a poset whose elements are all subsets of an
$Q_N$
, a poset whose elements are all subsets of an
![]() $N$
-element set equipped with set inclusion relation. For posets
$N$
-element set equipped with set inclusion relation. For posets
![]() $P$
and
$P$
and
![]() $Q$
, let the Boolean poset Ramsey number or simply poset Ramsey number
$Q$
, let the Boolean poset Ramsey number or simply poset Ramsey number
![]() $R(P,Q)$
be the least integer
$R(P,Q)$
be the least integer
![]() $N$
such that in any colouring of elements of the
$N$
such that in any colouring of elements of the
![]() $N$
-dimensional Boolean lattice
$N$
-dimensional Boolean lattice
![]() $Q_N$
in blue and red, there is an induced copy of
$Q_N$
in blue and red, there is an induced copy of
![]() $P$
with all blue elements or an induced copy of
$P$
with all blue elements or an induced copy of
![]() $Q$
with all red elements.
$Q$
with all red elements.
This function was first studied in detail relatively recently by Axenovich and Walzer [Reference Axenovich and Walzer1]. In the diagonal case
![]() $P=Q=Q_n$
, the bounds
$P=Q=Q_n$
, the bounds
![]() $2n+1 \leq R(Q_n, Q_n) \leq n^2 -n+2$
are the best currently known, see listed chronologically Walzer [Reference Walzer29], Axenovich and Walzer [Reference Axenovich and Walzer1], Cox and Stolee [Reference Cox and Stolee10], Lu and Thompson [Reference Lu and Thompson20], Bohman and Peng [Reference Bohman and Peng3]. Falgas-Ravry, Markström, Treglown, and Zhao [Reference Falgas-Ravry, Markström, Treglown and Zhao12] showed that
$2n+1 \leq R(Q_n, Q_n) \leq n^2 -n+2$
are the best currently known, see listed chronologically Walzer [Reference Walzer29], Axenovich and Walzer [Reference Axenovich and Walzer1], Cox and Stolee [Reference Cox and Stolee10], Lu and Thompson [Reference Lu and Thompson20], Bohman and Peng [Reference Bohman and Peng3]. Falgas-Ravry, Markström, Treglown, and Zhao [Reference Falgas-Ravry, Markström, Treglown and Zhao12] showed that
![]() $R(Q_3,Q_3)=7$
. Since any posets
$R(Q_3,Q_3)=7$
. Since any posets
![]() $P$
and
$P$
and
![]() $Q$
are induced subposets of
$Q$
are induced subposets of
![]() $Q_n$
for sufficiently large
$Q_n$
for sufficiently large
![]() $n$
, we see that
$n$
, we see that
![]() $R(P,Q)$
is well-defined. Boolean poset Ramsey numbers and their rainbow variants were considered for some special classes of posets by Chen, Chen, Cheng, Li, and Liu [Reference Chen, Chen, Cheng, Li and Liu7, Reference Chen, Cheng, Li and Liu8] as well as by Chang et al. [Reference Chang, Gerbner and Li6]. In the off-diagonal setting
$R(P,Q)$
is well-defined. Boolean poset Ramsey numbers and their rainbow variants were considered for some special classes of posets by Chen, Chen, Cheng, Li, and Liu [Reference Chen, Chen, Cheng, Li and Liu7, Reference Chen, Cheng, Li and Liu8] as well as by Chang et al. [Reference Chang, Gerbner and Li6]. In the off-diagonal setting
![]() $R(Q_m, Q_n)$
with
$R(Q_m, Q_n)$
with
![]() $m$
fixed and
$m$
fixed and
![]() $n$
large, an exact result is only known if
$n$
large, an exact result is only known if
![]() $m=1$
. It is easy to see that
$m=1$
. It is easy to see that
![]() $R(Q_1, Q_n)=n+1$
. For
$R(Q_1, Q_n)=n+1$
. For
![]() $m=2$
, it was shown in [Reference Axenovich and Walzer1] that
$m=2$
, it was shown in [Reference Axenovich and Walzer1] that
![]() $R(Q_2, Q_n) \leq 2n+2$
. This was improved by Lu and Thompson to
$R(Q_2, Q_n) \leq 2n+2$
. This was improved by Lu and Thompson to
![]() $R(Q_2, Q_n)\leq (5/3)n +2$
. Finally, it was further improved by Grósz, Methuku, and Tompkins [Reference Grósz, Methuku and Tompkins15]:
$R(Q_2, Q_n)\leq (5/3)n +2$
. Finally, it was further improved by Grósz, Methuku, and Tompkins [Reference Grósz, Methuku and Tompkins15]:
Theorem 1. (Grósz-Methuku-Tompkins [Reference Grósz, Methuku and Tompkins15]) For any
![]() $\epsilon \gt 0$
there is
$\epsilon \gt 0$
there is
![]() $n_0$
such that for any integer
$n_0$
such that for any integer
![]() $n\geq n_0$
, we have
$n\geq n_0$
, we have
![]() $n+3 \leq R(Q_2,Q_n) \le n + (2+\epsilon )n/\log n.$
$n+3 \leq R(Q_2,Q_n) \le n + (2+\epsilon )n/\log n.$
In this paper, we focus on
![]() $R(P, Q_n)$
for an arbitrary fixed poset
$R(P, Q_n)$
for an arbitrary fixed poset
![]() $P$
and large
$P$
and large
![]() $n$
. Note that
$n$
. Note that
![]() $R(P, Q_n)\geq n$
for any non-empty poset
$R(P, Q_n)\geq n$
for any non-empty poset
![]() $P$
as witnessed by a colouring of all elements of
$P$
as witnessed by a colouring of all elements of
![]() $Q_{n-1}$
in red. We prove that a central role is played by a small, three-element poset
$Q_{n-1}$
in red. We prove that a central role is played by a small, three-element poset
![]() $\Lambda = (\Lambda, {\lt} )$
, with elements
$\Lambda = (\Lambda, {\lt} )$
, with elements
![]() $Z_1, Z_2$
, and
$Z_1, Z_2$
, and
![]() $Z_3$
, such that
$Z_3$
, such that
![]() $Z_1\lt Z_3$
,
$Z_1\lt Z_3$
,
![]() $Z_2\lt Z_3$
, and
$Z_2\lt Z_3$
, and
![]() $Z_1$
and
$Z_1$
and
![]() $Z_2$
incomparable. A poset
$Z_2$
incomparable. A poset
![]() $V$
is the symmetric counterpart of
$V$
is the symmetric counterpart of
![]() $\Lambda$
, having elements
$\Lambda$
, having elements
![]() $Z_1, Z_2$
, and
$Z_1, Z_2$
, and
![]() $Z_3$
, such that
$Z_3$
, such that
![]() $Z_1\gt Z_3$
,
$Z_1\gt Z_3$
,
![]() $Z_2\gt Z_3$
, and
$Z_2\gt Z_3$
, and
![]() $Z_1$
and
$Z_1$
and
![]() $Z_2$
not comparable. Our main result shows a sharp jump in the behaviour of
$Z_2$
not comparable. Our main result shows a sharp jump in the behaviour of
![]() $R(P, Q_n)$
as a function of
$R(P, Q_n)$
as a function of
![]() $n$
depending whether or not
$n$
depending whether or not
![]() $P$
contains a copy
$P$
contains a copy
![]() $\Lambda$
or
$\Lambda$
or
![]() $V$
.
$V$
.
Theorem 2.
For every poset
![]() $P$
there is an
$P$
there is an
![]() $n_0\in{\mathbb{N}}$
such that for all
$n_0\in{\mathbb{N}}$
such that for all
![]() $n\gt n_0$
the following holds.
$n\gt n_0$
the following holds.
-
If
 $P$
contains a copy of
$P$
contains a copy of
 $\Lambda$
or
$\Lambda$
or
 $V$
, then
$V$
, then
 $R(P, Q_n) \geq n + \frac{1}{15} \frac{n}{\log n}$
.
$R(P, Q_n) \geq n + \frac{1}{15} \frac{n}{\log n}$
. -
If
 $P$
contains neither a copy of
$P$
contains neither a copy of
 $\Lambda$
nor a copy of
$\Lambda$
nor a copy of
 $V$
, then
$V$
, then
 $R(P, Q_n) \leq n + f(P)$
, for some function
$R(P, Q_n) \leq n + f(P)$
, for some function
 $f$
.
$f$
.
The first part of Theorem 2 relies on the lower bound on
![]() $R(\Lambda,Q_n)$
that we provide in the next theorem along with an asymptotically matching upper bound.
$R(\Lambda,Q_n)$
that we provide in the next theorem along with an asymptotically matching upper bound.
Theorem 3.
Let
![]() $\epsilon \gt 0$
. There exists an
$\epsilon \gt 0$
. There exists an
![]() $n_0\in{\mathbb{N}}$
such that for all
$n_0\in{\mathbb{N}}$
such that for all
![]() $n\ge n_0$
,
$n\ge n_0$
,
 \begin{equation*}n+ \frac {1}{15}\cdot \frac {n}{\log n}\leq R(\Lambda,Q_n)\le n+ \big (1+\epsilon )\cdot \frac {n}{\log n}.\end{equation*}
\begin{equation*}n+ \frac {1}{15}\cdot \frac {n}{\log n}\leq R(\Lambda,Q_n)\le n+ \big (1+\epsilon )\cdot \frac {n}{\log n}.\end{equation*}
More precisely, it can be seen that the lower bound holds for
![]() $\log n_0\ge 535$
, while the upper bound requires
$\log n_0\ge 535$
, while the upper bound requires
![]() $\log n_0\ge \frac{36}{\epsilon ^2}$
. Note that
$\log n_0\ge \frac{36}{\epsilon ^2}$
. Note that
![]() $R(\Lambda,Q_n)\le R(Q_2,Q_n)$
, so Theorem 1 already implies a bound for
$R(\Lambda,Q_n)\le R(Q_2,Q_n)$
, so Theorem 1 already implies a bound for
![]() $R(\Lambda,Q_n)$
which is weaker but asymptotically equal to the upper bound of Theorem 3. Our main tool used to prove both the lower and the improved upper bound on
$R(\Lambda,Q_n)$
which is weaker but asymptotically equal to the upper bound of Theorem 3. Our main tool used to prove both the lower and the improved upper bound on
![]() $R(\Lambda, Q_n)$
is a structural duality statement, Theorem 12. The upper bound is obtained from that using a counting argument, while for the lower bound we give a probabilistic construction to find a desired colouring. This is the first of a kind non-marginal improvement of a trivial lower bound for poset Ramsey numbers. Most other known lower bounds correspond to so-called layered colourings of Boolean lattices, where any two elements of the same size have the same colour. The only two previously given non-layered constructions are those from Theorem 1 by Grósz, Methuku, and Tompkins [Reference Grósz, Methuku and Tompkins15], improving the trivial lower bound
$R(\Lambda, Q_n)$
is a structural duality statement, Theorem 12. The upper bound is obtained from that using a counting argument, while for the lower bound we give a probabilistic construction to find a desired colouring. This is the first of a kind non-marginal improvement of a trivial lower bound for poset Ramsey numbers. Most other known lower bounds correspond to so-called layered colourings of Boolean lattices, where any two elements of the same size have the same colour. The only two previously given non-layered constructions are those from Theorem 1 by Grósz, Methuku, and Tompkins [Reference Grósz, Methuku and Tompkins15], improving the trivial lower bound
![]() $R(Q_2, Q_n) \geq n+2$
to
$R(Q_2, Q_n) \geq n+2$
to
![]() $n+3$
and by Bohman and Peng [Reference Bohman and Peng3] improving the trivial lower bound for the diagonal case
$n+3$
and by Bohman and Peng [Reference Bohman and Peng3] improving the trivial lower bound for the diagonal case
![]() $R(Q_n,Q_n)\ge 2n$
to
$R(Q_n,Q_n)\ge 2n$
to
![]() $2n+1$
.
$2n+1$
.
Theorems 1 and 2 also give a lower bound for
![]() $R(Q_2, Q_n)$
which is asymptotically tight not only in the first but also in the second summand.
$R(Q_2, Q_n)$
which is asymptotically tight not only in the first but also in the second summand.
Corollary 4.
![]() $R(Q_2,Q_n) = n + \Theta \left (\frac{n}{\log (n)}\right ).$
$R(Q_2,Q_n) = n + \Theta \left (\frac{n}{\log (n)}\right ).$
Note that the Ramsey variant we consider is related to extremal problems on posets and their induced subposets. Carroll and Katona [Reference Carroll and Katona5] introduced a Turán-type function
![]() $La^{\#}(n, P)$
as the largest number of elements in
$La^{\#}(n, P)$
as the largest number of elements in
![]() $Q_n$
that do not induce a copy of the poset
$Q_n$
that do not induce a copy of the poset
![]() $P$
. Most notable is a result by Methuku and Pálvölgyi [Reference Methuku and Pálvölgyi22], who showed that
$P$
. Most notable is a result by Methuku and Pálvölgyi [Reference Methuku and Pálvölgyi22], who showed that
![]() $La^{\#}(n,P) \leq f(P) \binom{n}{\lfloor n/2 \rfloor }$
, thus proving a conjecture of Katona, Lu, and Milans [Reference Lu and Milans19]. Their statement has been refined for several special cases, see for example Lu and Milans [Reference Lu and Milans19] and Méroueh [Reference Méroueh21], as well as an earlier result by Boehlein and Jiang [Reference Boehnlein and Jiang2]. Further Turán-type results were given by Methuku and Tompkins [Reference Methuku and Tompkins23] and Tomon [Reference Tomon28]. Note that the corresponding function
$La^{\#}(n,P) \leq f(P) \binom{n}{\lfloor n/2 \rfloor }$
, thus proving a conjecture of Katona, Lu, and Milans [Reference Lu and Milans19]. Their statement has been refined for several special cases, see for example Lu and Milans [Reference Lu and Milans19] and Méroueh [Reference Méroueh21], as well as an earlier result by Boehlein and Jiang [Reference Boehnlein and Jiang2]. Further Turán-type results were given by Methuku and Tompkins [Reference Methuku and Tompkins23] and Tomon [Reference Tomon28]. Note that the corresponding function
![]() $La(n,P)$
for non-induced, so-called weak subposet,
$La(n,P)$
for non-induced, so-called weak subposet,
![]() $P$
, was extensively studied, see for example [Reference Bukh4, Reference Chen and Li9, Reference Erdős11, Reference Griggs and Katona13, Reference Griggs and Lu14, Reference Grósz, Methuku and Tompkins16, Reference Patkós26, Reference Sperner27]. In addition, saturation-type extremal problems have been addressed for induced and weak subposets, see a recent paper of Keszegh, Lemons, Martin, Pálvölgyi, and Patkós [Reference Keszegh, Lemons, Martin, Pálvölgyi and Patkós17].
$P$
, was extensively studied, see for example [Reference Bukh4, Reference Chen and Li9, Reference Erdős11, Reference Griggs and Katona13, Reference Griggs and Lu14, Reference Grósz, Methuku and Tompkins16, Reference Patkós26, Reference Sperner27]. In addition, saturation-type extremal problems have been addressed for induced and weak subposets, see a recent paper of Keszegh, Lemons, Martin, Pálvölgyi, and Patkós [Reference Keszegh, Lemons, Martin, Pálvölgyi and Patkós17].
The structure of the paper is as follows. In Section 2, we give the formal definitions and notations, define special posets we call factorial trees and shrubs, and prove some basic properties. In Section 2.4, we provide an alternative proof of the upper bound in Theorem 1. This makes our paper self-contained since we need this result for Corollary 4. In Section 3, we provide a structural duality statement, Theorem 12, which is the key tool for the main proofs. In Section 4, we use a probabilistic construction to find a colouring with ‘good’ properties. Lastly, in Section 5 we complete the proofs of Theorems 3 and 2.
2. Preliminaries
2.1. Basic notations and definitions
A poset is a set
![]() $P$
equipped with a relation
$P$
equipped with a relation
![]() $\le _P$
that is transitive, reflexive, and antisymmetric. For any non-empty set
$\le _P$
that is transitive, reflexive, and antisymmetric. For any non-empty set
![]() $\mathcal{X}$
, let
$\mathcal{X}$
, let
![]() ${\mathcal{Q}}({\mathcal{X}})$
be the Boolean lattice of dimension
${\mathcal{Q}}({\mathcal{X}})$
be the Boolean lattice of dimension
![]() $|{\mathcal{X}}|$
on a ground set
$|{\mathcal{X}}|$
on a ground set
![]() $\mathcal{X}$
, that is the poset consisting of all subsets of
$\mathcal{X}$
, that is the poset consisting of all subsets of
![]() $\mathcal{X}$
equipped with the inclusion relation
$\mathcal{X}$
equipped with the inclusion relation
![]() $\subseteq$
. We use
$\subseteq$
. We use
![]() $Q_N$
to denote a Boolean lattice of dimension
$Q_N$
to denote a Boolean lattice of dimension
![]() $N$
, that is a set of all subsets of an
$N$
, that is a set of all subsets of an
![]() $N$
-element set with set inclusion order. We refer to a poset either as a pair
$N$
-element set with set inclusion order. We refer to a poset either as a pair
![]() $(P, \leq _P)$
, or, when it is clear from context, simply as a set
$(P, \leq _P)$
, or, when it is clear from context, simply as a set
![]() $P$
. The elements of
$P$
. The elements of
![]() $P$
are often called vertices.
$P$
are often called vertices.
For two posets
![]() $(P_1, \leq _{P_1}\!)$
and
$(P_1, \leq _{P_1}\!)$
and
![]() $(P_2, \leq _{P_2}\!)$
, an embedding
$(P_2, \leq _{P_2}\!)$
, an embedding
![]() $\phi \,:\, P_1\to P_2$
of
$\phi \,:\, P_1\to P_2$
of
![]() $P_1$
into
$P_1$
into
![]() $P_2$
is an injective function such that for every
$P_2$
is an injective function such that for every
![]() $X_1,X_2\in P_1$
,
$X_1,X_2\in P_1$
,
![]() $X_1 \leq _{P_1} X_2\text{ if and only if }\phi (X_1)\leq _{P_2} \phi (X_2).$
A poset
$X_1 \leq _{P_1} X_2\text{ if and only if }\phi (X_1)\leq _{P_2} \phi (X_2).$
A poset
![]() $P_1$
is an induced subposet of
$P_1$
is an induced subposet of
![]() $P_2$
if
$P_2$
if
![]() $P_1\subseteq P_2$
and for every
$P_1\subseteq P_2$
and for every
![]() $X_1,X_2\in P_1$
,
$X_1,X_2\in P_1$
,
![]() $X_1 \leq _{P_1} X_2$
if and only if
$X_1 \leq _{P_1} X_2$
if and only if
![]() $X_1 \leq _{P_2} X_2.$
A copy of a poset
$X_1 \leq _{P_2} X_2.$
A copy of a poset
![]() $P_1$
in
$P_1$
in
![]() $P_2$
is an induced subposet
$P_2$
is an induced subposet
![]() $P^{\prime}$
of
$P^{\prime}$
of
![]() $P_2$
, isomorphic to
$P_2$
, isomorphic to
![]() $P_1$
.
$P_1$
.
Consider an assignment of two colours, blue and red, to the vertices of posets. Such a colouring
![]() $c: P \rightarrow \{blue, red\}$
is a blue/red colouring of
$c: P \rightarrow \{blue, red\}$
is a blue/red colouring of
![]() $P$
. A coloured poset is monochromatic if all of its vertices share the same colour. A monochromatic poset whose vertices are blue is called a blue poset. Similarly defined is a red poset. Using this terminology, the poset Ramsey number of two posets
$P$
. A coloured poset is monochromatic if all of its vertices share the same colour. A monochromatic poset whose vertices are blue is called a blue poset. Similarly defined is a red poset. Using this terminology, the poset Ramsey number of two posets
![]() $P$
and
$P$
and
![]() $Q$
is
$Q$
is
Let
![]() $\mathcal{X}$
and
$\mathcal{X}$
and
![]() $\mathcal{Y}$
be disjoint sets. Then the vertices of the Boolean lattice
$\mathcal{Y}$
be disjoint sets. Then the vertices of the Boolean lattice
![]() ${\mathcal{Q}}({\mathcal{X}}\cup{\mathcal{Y}})$
, that is the unordered subsets of
${\mathcal{Q}}({\mathcal{X}}\cup{\mathcal{Y}})$
, that is the unordered subsets of
![]() ${\mathcal{X}}\cup{\mathcal{Y}}$
, can be partitioned with respect to
${\mathcal{X}}\cup{\mathcal{Y}}$
, can be partitioned with respect to
![]() $\mathcal{X}$
and
$\mathcal{X}$
and
![]() $\mathcal{Y}$
in the following manner. Every
$\mathcal{Y}$
in the following manner. Every
![]() $Z\subseteq{\mathcal{X}}\cup{\mathcal{Y}}$
has an
$Z\subseteq{\mathcal{X}}\cup{\mathcal{Y}}$
has an
![]() $\mathcal{X}$
-part
$\mathcal{X}$
-part
![]() $X_Z=Z\cap{\mathcal{X}}$
and a
$X_Z=Z\cap{\mathcal{X}}$
and a
![]() $\mathcal{Y}$
-part
$\mathcal{Y}$
-part
![]() $Y_Z=Z\cap{\mathcal{Y}}$
. In this setting, we refer to
$Y_Z=Z\cap{\mathcal{Y}}$
. In this setting, we refer to
![]() $Z$
alternatively as the pair
$Z$
alternatively as the pair
![]() $(X_Z,Y_Z)$
. Conversely, for all
$(X_Z,Y_Z)$
. Conversely, for all
![]() $X\subseteq{\mathcal{X}}$
,
$X\subseteq{\mathcal{X}}$
,
![]() $Y\subseteq{\mathcal{Y}}$
, the pair
$Y\subseteq{\mathcal{Y}}$
, the pair
![]() $(X,Y)$
has a
$(X,Y)$
has a
![]() $1$
-to-
$1$
-to-
![]() $1$
correspondence to the vertex
$1$
correspondence to the vertex
![]() $X\cup Y\in{\mathcal{Q}}({\mathcal{X}}\cup{\mathcal{Y}})$
. One can think of such pairs as elements of the Cartesian product
$X\cup Y\in{\mathcal{Q}}({\mathcal{X}}\cup{\mathcal{Y}})$
. One can think of such pairs as elements of the Cartesian product
![]() $2^{\mathcal{X}} \times 2^{\mathcal{Y}}$
which has a canonical bijection to
$2^{\mathcal{X}} \times 2^{\mathcal{Y}}$
which has a canonical bijection to
![]() $2^{{\mathcal{X}}\cup{\mathcal{Y}}}={\mathcal{Q}}({\mathcal{X}}\cup{\mathcal{Y}})$
. Observe that for
$2^{{\mathcal{X}}\cup{\mathcal{Y}}}={\mathcal{Q}}({\mathcal{X}}\cup{\mathcal{Y}})$
. Observe that for
![]() $X_i\subseteq{\mathcal{X}}, Y_i\subseteq{\mathcal{Y}}$
,
$X_i\subseteq{\mathcal{X}}, Y_i\subseteq{\mathcal{Y}}$
,
![]() $i\in [2]$
, we have
$i\in [2]$
, we have
![]() $(X_1,Y_1)\subseteq (X_2,Y_2)$
if and only if
$(X_1,Y_1)\subseteq (X_2,Y_2)$
if and only if
![]() $X_1\subseteq X_2$
and
$X_1\subseteq X_2$
and
![]() $Y_1\subseteq Y_2$
.
$Y_1\subseteq Y_2$
.
For any poset, we refer to vertices
![]() $Z_1,Z_2$
which are incomparable as
$Z_1,Z_2$
which are incomparable as
![]() $Z_1\nsim Z_2$
. For a positive integer
$Z_1\nsim Z_2$
. For a positive integer
![]() $n\in{\mathbb{N}}$
, we use
$n\in{\mathbb{N}}$
, we use
![]() $[n]$
to denote the set
$[n]$
to denote the set
![]() $\{1,\ldots,n\}$
. Given an integer
$\{1,\ldots,n\}$
. Given an integer
![]() $n\in{\mathbb{N}}$
and a set
$n\in{\mathbb{N}}$
and a set
![]() $\mathcal{X}$
, let
$\mathcal{X}$
, let
![]() $\binom{{\mathcal{X}}}{n}$
be the set of all
$\binom{{\mathcal{X}}}{n}$
be the set of all
![]() $n$
-element subsets of
$n$
-element subsets of
![]() $\mathcal{X}$
. Throughout the paper, ‘
$\mathcal{X}$
. Throughout the paper, ‘
![]() $\log$
’ always refers to the logarithm with base
$\log$
’ always refers to the logarithm with base
![]() $2$
, while ‘
$2$
, while ‘
![]() $\ln$
’ refers to the natural logarithm. For sets
$\ln$
’ refers to the natural logarithm. For sets
![]() $A$
and
$A$
and
![]() $B$
, we write
$B$
, we write
![]() $A\subset B$
to denote that
$A\subset B$
to denote that
![]() $A$
is a proper subset of
$A$
is a proper subset of
![]() $B$
. We omit floors and ceilings where appropriate.
$B$
. We omit floors and ceilings where appropriate.
2.2. Structure of posets with forbidden
 $\Lambda$
or
$\Lambda$
or
 $V$
$V$
A poset
![]() $\mathcal{T}$
is an up-tree if there is a unique minimal vertex in
$\mathcal{T}$
is an up-tree if there is a unique minimal vertex in
![]() $\mathcal{T}$
and for every vertex
$\mathcal{T}$
and for every vertex
![]() $X\in{\mathcal{T}}$
, the set
$X\in{\mathcal{T}}$
, the set
![]() $\{Y\in{\mathcal{T}}\,:\, Y\le X\}$
is a chain, that is its vertices are pairwise comparable. We say that two subposets of a given poset are independent if they are vertexwise incomparable. Furthermore, a collection of subposets is independent if they are pairwise independent. We use this notation to describe posets which don’t contain a copy of
$\{Y\in{\mathcal{T}}\,:\, Y\le X\}$
is a chain, that is its vertices are pairwise comparable. We say that two subposets of a given poset are independent if they are vertexwise incomparable. Furthermore, a collection of subposets is independent if they are pairwise independent. We use this notation to describe posets which don’t contain a copy of
![]() $\Lambda$
(or
$\Lambda$
(or
![]() $V$
).
$V$
).
Lemma 5.
Let
![]() $P$
be a poset. There is no copy of
$P$
be a poset. There is no copy of
![]() $\Lambda$
in
$\Lambda$
in
![]() $P$
if and only if
$P$
if and only if
![]() $P$
is an independent collection of up-trees.
$P$
is an independent collection of up-trees.
Proof. Observe that a poset
![]() $P$
is an independent collection of up-trees if and only if for every vertex
$P$
is an independent collection of up-trees if and only if for every vertex
![]() $X\in P$
,
$X\in P$
,
![]() $\{Y\in P\,:\, Y\le X\}$
forms a chain.
$\{Y\in P\,:\, Y\le X\}$
forms a chain.
Suppose that there is a copy of
![]() $\Lambda$
in
$\Lambda$
in
![]() $P$
on vertices
$P$
on vertices
![]() $Z_i$
,
$Z_i$
,
![]() $i\in [3]$
with
$i\in [3]$
with
![]() $Z_1\lt Z_3$
,
$Z_1\lt Z_3$
,
![]() $Z_2\lt Z_3$
and
$Z_2\lt Z_3$
and
![]() $Z_1\nsim Z_2$
. Then
$Z_1\nsim Z_2$
. Then
![]() $Z_1,Z_2$
witness that
$Z_1,Z_2$
witness that
![]() $\{Y\in P\,:\, Y\lt Z_3\}$
is not a chain, so
$\{Y\in P\,:\, Y\lt Z_3\}$
is not a chain, so
![]() $P$
is not an independent collection of up-trees.
$P$
is not an independent collection of up-trees.
Now assume that
![]() $P$
is not an independent collection of up-trees. Then there exist some
$P$
is not an independent collection of up-trees. Then there exist some
![]() $X\in P$
and
$X\in P$
and
![]() $Z_1,Z_2 \in \{Y\in P\,:\, Y\le X\}$
such that
$Z_1,Z_2 \in \{Y\in P\,:\, Y\le X\}$
such that
![]() $Z_1\nsim Z_2$
. Since
$Z_1\nsim Z_2$
. Since
![]() $X$
is comparable to all vertices in
$X$
is comparable to all vertices in
![]() $\{Y\in P\,:\, Y\le X\}$
,
$\{Y\in P\,:\, Y\le X\}$
,
![]() $X\gt Z_1, X\gt Z_2$
. Now
$X\gt Z_1, X\gt Z_2$
. Now
![]() $X,Z_1,Z_2$
form a copy of
$X,Z_1,Z_2$
form a copy of
![]() $\Lambda$
.
$\Lambda$
.![]()
By symmetry an analogous statement holds for posets with forbidden induced copy of
![]() $V$
. If we forbid both
$V$
. If we forbid both
![]() $V$
and
$V$
and
![]() $\Lambda$
simultaneously we obtain the following structure.
$\Lambda$
simultaneously we obtain the following structure.
Corollary 6.
Let
![]() $P$
be a poset such that there is neither a copy of
$P$
be a poset such that there is neither a copy of
![]() $V$
nor of
$V$
nor of
![]() $\Lambda$
. Then
$\Lambda$
. Then
![]() $P$
is an independent collection of chains.
$P$
is an independent collection of chains.
2.3. Embeddings of
 $Q_n$
$Q_n$
When considering an embedding
![]() $\phi$
of a Boolean lattice
$\phi$
of a Boolean lattice
![]() $Q_n$
into a larger Boolean lattice
$Q_n$
into a larger Boolean lattice
![]() ${\mathcal{Q}}({\mathcal{Z}})$
, we can partition
${\mathcal{Q}}({\mathcal{Z}})$
, we can partition
![]() $\mathcal{Z}$
such that it has the following nice property. This result is due to Axenovich and Walzer [Reference Axenovich and Walzer1], here we state an alternative proof.
$\mathcal{Z}$
such that it has the following nice property. This result is due to Axenovich and Walzer [Reference Axenovich and Walzer1], here we state an alternative proof.
Lemma 7. (Axenovich-Walzer [Reference Axenovich and Walzer1]). Let
![]() $n\in{\mathbb{N}}$
. Let
$n\in{\mathbb{N}}$
. Let
![]() $\mathcal{Z}$
be a set with
$\mathcal{Z}$
be a set with
![]() $|{\mathcal{Z}}|\gt n$
and let
$|{\mathcal{Z}}|\gt n$
and let
![]() $Q={\mathcal{Q}}({\mathcal{Z}})$
. If there is an embedding
$Q={\mathcal{Q}}({\mathcal{Z}})$
. If there is an embedding
![]() $\phi \,:\, Q_n\to Q$
, then there exist a subset
$\phi \,:\, Q_n\to Q$
, then there exist a subset
![]() ${\mathcal{X}}\subset {\mathcal{Z}}$
with
${\mathcal{X}}\subset {\mathcal{Z}}$
with
![]() $|{\mathcal{X}}|=n$
, and an embedding
$|{\mathcal{X}}|=n$
, and an embedding
![]() $\phi^{\prime}\,:\,{\mathcal{Q}}({\mathcal{X}})\to Q$
with the same image as
$\phi^{\prime}\,:\,{\mathcal{Q}}({\mathcal{X}})\to Q$
with the same image as
![]() $\phi$
such that
$\phi$
such that
![]() $\phi^{\prime}(X)\cap{\mathcal{X}}=X$
for all
$\phi^{\prime}(X)\cap{\mathcal{X}}=X$
for all
![]() $X\subseteq{\mathcal{X}}$
.
$X\subseteq{\mathcal{X}}$
.
Proof. Let the ground set of
![]() $Q_n$
be
$Q_n$
be
![]() ${\mathcal{X}}^{\prime}$
. We consider the embedding of singletons of
${\mathcal{X}}^{\prime}$
. We consider the embedding of singletons of
![]() $Q_n$
, that is
$Q_n$
, that is
![]() $\phi (\{a\})$
,
$\phi (\{a\})$
,
![]() $a\in{\mathcal{X}}^{\prime}$
. If
$a\in{\mathcal{X}}^{\prime}$
. If
![]() $\phi (\{a\})\subseteq \bigcup _{X^{\prime}\subseteq{\mathcal{X}}^{\prime}\backslash \{a\}} \phi (X^{\prime})$
, then
$\phi (\{a\})\subseteq \bigcup _{X^{\prime}\subseteq{\mathcal{X}}^{\prime}\backslash \{a\}} \phi (X^{\prime})$
, then
![]() $\phi (\{a\})\subseteq \bigcup _{X^{\prime}\subseteq{\mathcal{X}}^{\prime}\backslash \{a\}} \phi (X^{\prime}) \subseteq \phi ({\mathcal{X}}^{\prime}\backslash \{a\})$
. But
$\phi (\{a\})\subseteq \bigcup _{X^{\prime}\subseteq{\mathcal{X}}^{\prime}\backslash \{a\}} \phi (X^{\prime}) \subseteq \phi ({\mathcal{X}}^{\prime}\backslash \{a\})$
. But
![]() $\{a\}\nsubseteq{\mathcal{X}}^{\prime}\backslash \{a\}$
and
$\{a\}\nsubseteq{\mathcal{X}}^{\prime}\backslash \{a\}$
and
![]() $\phi$
is an embedding, a contradiction. Thus
$\phi$
is an embedding, a contradiction. Thus
![]() $\phi (\{a\})\not \subseteq \bigcup _{X^{\prime}\subseteq{\mathcal{X}}^{\prime}\backslash \{a\}} \phi (X^{\prime})$
. For every
$\phi (\{a\})\not \subseteq \bigcup _{X^{\prime}\subseteq{\mathcal{X}}^{\prime}\backslash \{a\}} \phi (X^{\prime})$
. For every
![]() $a\in{\mathcal{X}}^{\prime}$
, pick an arbitrary
$a\in{\mathcal{X}}^{\prime}$
, pick an arbitrary
Note that
![]() $b(a_1)\notin \phi (\{a_2\})$
for any
$b(a_1)\notin \phi (\{a_2\})$
for any
![]() $a_1,a_2\in{\mathcal{X}}^{\prime}$
,
$a_1,a_2\in{\mathcal{X}}^{\prime}$
,
![]() $a_1\neq a_2$
, so all representatives are distinct. Let
$a_1\neq a_2$
, so all representatives are distinct. Let
![]() ${\mathcal{X}}=\{b(a) \,:\, a\in{\mathcal{X}}^{\prime}\}$
. We see that the map
${\mathcal{X}}=\{b(a) \,:\, a\in{\mathcal{X}}^{\prime}\}$
. We see that the map
![]() $b:{\mathcal{X}}^{\prime} \to{\mathcal{X}}$
is a bijection. For every
$b:{\mathcal{X}}^{\prime} \to{\mathcal{X}}$
is a bijection. For every
![]() $B\subseteq{\mathcal{X}}$
, let
$B\subseteq{\mathcal{X}}$
, let
![]() $A_B\subseteq{\mathcal{X}}^{\prime}$
be such that
$A_B\subseteq{\mathcal{X}}^{\prime}$
be such that
![]() $B=\{b(a): a \in A_B\}$
. We define
$B=\{b(a): a \in A_B\}$
. We define
![]() $\phi^{\prime}\,:\,{\mathcal{Q}}({\mathcal{X}})\to Q$
as follows:
$\phi^{\prime}\,:\,{\mathcal{Q}}({\mathcal{X}})\to Q$
as follows:
![]() $\phi^{\prime}(B) = \phi (A_B)$
,
$\phi^{\prime}(B) = \phi (A_B)$
,
![]() $B\in{\mathcal{X}}$
. Then
$B\in{\mathcal{X}}$
. Then
![]() $\phi^{\prime}$
is an embedding. Observe that for
$\phi^{\prime}$
is an embedding. Observe that for
![]() $X\subseteq{\mathcal{X}}$
and
$X\subseteq{\mathcal{X}}$
and
![]() $b\in{\mathcal{X}}$
,
$b\in{\mathcal{X}}$
,
![]() $b\in \phi^{\prime}(X)$
if and only if
$b\in \phi^{\prime}(X)$
if and only if
![]() $b\in X$
. Thus
$b\in X$
. Thus
![]() $\phi^{\prime}(X)\cap{\mathcal{X}}=X$
for all
$\phi^{\prime}(X)\cap{\mathcal{X}}=X$
for all
![]() $X\subseteq{\mathcal{X}}$
. This concludes the proof.
$X\subseteq{\mathcal{X}}$
. This concludes the proof.![]()
We call an embedding
![]() $\phi$
of
$\phi$
of
![]() ${\mathcal{Q}}({\mathcal{X}})$
into
${\mathcal{Q}}({\mathcal{X}})$
into
![]() ${\mathcal{Q}}({\mathcal{X}}\cup{\mathcal{Y}})$
for disjoint
${\mathcal{Q}}({\mathcal{X}}\cup{\mathcal{Y}})$
for disjoint
![]() $\mathcal{X}$
and
$\mathcal{X}$
and
![]() $\mathcal{Y}$
,
$\mathcal{Y}$
,
![]() $\mathcal{X}$
-good if
$\mathcal{X}$
-good if
![]() $\phi (X)\cap{\mathcal{X}} = X$
for all
$\phi (X)\cap{\mathcal{X}} = X$
for all
![]() $X\in{\mathcal{X}}$
. We also call a copy
$X\in{\mathcal{X}}$
. We also call a copy
![]() $Q$
of
$Q$
of
![]() ${\mathcal{Q}}({\mathcal{X}})$
in
${\mathcal{Q}}({\mathcal{X}})$
in
![]() ${\mathcal{Q}}({\mathcal{X}}\cup{\mathcal{Y}})$
${\mathcal{Q}}({\mathcal{X}}\cup{\mathcal{Y}})$
![]() $\mathcal{X}$
-good if there is an
$\mathcal{X}$
-good if there is an
![]() $\mathcal{X}$
-good embedding of
$\mathcal{X}$
-good embedding of
![]() ${\mathcal{Q}}({\mathcal{X}})$
into
${\mathcal{Q}}({\mathcal{X}})$
into
![]() ${\mathcal{Q}}({\mathcal{X}}\cup{\mathcal{Y}})$
.
${\mathcal{Q}}({\mathcal{X}}\cup{\mathcal{Y}})$
.
Lemma 7 claims in particular that for any copy of
![]() $Q_n$
in a larger Boolean lattice
$Q_n$
in a larger Boolean lattice
![]() $Q$
, there is a subset
$Q$
, there is a subset
![]() $\mathcal{X}$
of the ground set of
$\mathcal{X}$
of the ground set of
![]() $Q$
with
$Q$
with
![]() $|{\mathcal{X}}|=n$
such that there is an
$|{\mathcal{X}}|=n$
such that there is an
![]() $\mathcal{X}$
-good copy of
$\mathcal{X}$
-good copy of
![]() ${\mathcal{Q}}({\mathcal{X}})$
in
${\mathcal{Q}}({\mathcal{X}})$
in
![]() $Q$
.
$Q$
.
2.4. Red copy of
 $Q_n$
vs. blue chain
$Q_n$
vs. blue chain
The main goal of this subsection is to present an alternative proof for the upper bound of Theorem 1 and thus of Corollary 4. Grósz, Methuku, and Tompkins [Reference Grósz, Methuku and Tompkins15] stated the following lemma using a different formulation. While they used algorithmic tools in their proof, we prove the statement recursively. Recall that for a given partition
![]() ${\mathcal{X}}\cup{\mathcal{Y}}$
of the ground set of a Boolean lattice we denote a vertex
${\mathcal{X}}\cup{\mathcal{Y}}$
of the ground set of a Boolean lattice we denote a vertex
![]() $X\cup Y\in{\mathcal{Q}}({\mathcal{X}}\cup{\mathcal{Y}})$
, where
$X\cup Y\in{\mathcal{Q}}({\mathcal{X}}\cup{\mathcal{Y}})$
, where
![]() $X\subseteq{\mathcal{X}}, Y\subseteq{\mathcal{Y}}$
, as
$X\subseteq{\mathcal{X}}, Y\subseteq{\mathcal{Y}}$
, as
![]() $(X,Y)$
.
$(X,Y)$
.
Lemma 8.
Let
![]() $\mathcal{X}$
,
$\mathcal{X}$
,
![]() $\mathcal{Y}$
be disjoint sets with
$\mathcal{Y}$
be disjoint sets with
![]() $|{\mathcal{X}}|=n$
and
$|{\mathcal{X}}|=n$
and
![]() $|{\mathcal{Y}}|=k$
, for some
$|{\mathcal{Y}}|=k$
, for some
![]() $n,k\in{\mathbb{N}}$
. Let
$n,k\in{\mathbb{N}}$
. Let
![]() $Q={\mathcal{Q}}({\mathcal{X}}\cup{\mathcal{Y}})$
be a blue/red coloured Boolean lattice. Fix some linear ordering
$Q={\mathcal{Q}}({\mathcal{X}}\cup{\mathcal{Y}})$
be a blue/red coloured Boolean lattice. Fix some linear ordering
![]() $\pi =(y_1,\ldots,y_k)$
of
$\pi =(y_1,\ldots,y_k)$
of
![]() $\mathcal{Y}$
and define
$\mathcal{Y}$
and define
![]() $Y(0), \ldots, Y(k)$
by
$Y(0), \ldots, Y(k)$
by
![]() $Y(0)=\varnothing$
and
$Y(0)=\varnothing$
and
![]() $Y(i)=\{y_1,\ldots,y_i\}$
for
$Y(i)=\{y_1,\ldots,y_i\}$
for
![]() $i\in [k]$
. Then there exists at least one of the following in
$i\in [k]$
. Then there exists at least one of the following in
![]() $Q$
:
$Q$
:
-
(1) a red
 $\mathcal{X}$
-good copy of
$\mathcal{X}$
-good copy of
 ${\mathcal{Q}}({\mathcal{X}})$
, or
${\mathcal{Q}}({\mathcal{X}})$
, or
-
(2) a blue chain of length
 $k+1$
of the form
$k+1$
of the form
 $(X_0,Y(0)),\ldots,(X_{k},Y(k))$
where
$(X_0,Y(0)),\ldots,(X_{k},Y(k))$
where
 $X_0 \subseteq X_1 \subseteq \ldots \subseteq X_k\subseteq{\mathcal{X}}$
.
$X_0 \subseteq X_1 \subseteq \ldots \subseteq X_k\subseteq{\mathcal{X}}$
.
Proof. Suppose that there is no blue chain as described in (b). For every
![]() $X\subseteq{\mathcal{X}}$
, we recursively define a label
$X\subseteq{\mathcal{X}}$
, we recursively define a label
![]() $\ell _X\in \{0,\ldots,k\}$
such that
$\ell _X\in \{0,\ldots,k\}$
such that
![]() $\phi \,:\,{\mathcal{Q}}({\mathcal{X}})\to Q$
,
$\phi \,:\,{\mathcal{Q}}({\mathcal{X}})\to Q$
,
![]() $\phi (X)=(X,Y(\ell _X))$
, is an embedding with monochromatic red image. We require
$\phi (X)=(X,Y(\ell _X))$
, is an embedding with monochromatic red image. We require
![]() $\ell _X$
to fulfil three properties:
$\ell _X$
to fulfil three properties:
-
(1) For any
 $X^{\prime}\subseteq X$
,
$X^{\prime}\subseteq X$
,
 $\ell _{X^{\prime}}\le \ell _{X}$
.
$\ell _{X^{\prime}}\le \ell _{X}$
. -
(2) There is a blue chain of length
 $\ell _X$
contained in the Boolean lattice with ground set
$\ell _X$
contained in the Boolean lattice with ground set
 $X\cup Y(\ell _X)$
, which we denote by
$X\cup Y(\ell _X)$
, which we denote by
 $Q^{X}$
.
$Q^{X}$
. -
(3)
 $(X,Y(\ell _X))$
is red.
$(X,Y(\ell _X))$
is red.
First, consider the vertex
![]() $\varnothing$
. Let
$\varnothing$
. Let
![]() $\ell _\varnothing$
be the minimum
$\ell _\varnothing$
be the minimum
![]() $\ell$
,
$\ell$
,
![]() $0\le \ell \le k$
, such that
$0\le \ell \le k$
, such that
![]() $(\varnothing,Y(\ell ))$
is red. If such an
$(\varnothing,Y(\ell ))$
is red. If such an
![]() $\ell$
does not exist, then
$\ell$
does not exist, then
![]() $(\varnothing,Y(0)), \ldots, (\varnothing,Y(k))$
form a blue chain, a contradiction. It is clear to see that Properties (1) and (3) hold. If
$(\varnothing,Y(0)), \ldots, (\varnothing,Y(k))$
form a blue chain, a contradiction. It is clear to see that Properties (1) and (3) hold. If
![]() $\ell _\varnothing =0$
, (2) is trivially true. If
$\ell _\varnothing =0$
, (2) is trivially true. If
![]() $\ell _\varnothing \ge 1$
,
$\ell _\varnothing \ge 1$
,
![]() $(\varnothing,Y(0)), \ldots, (\varnothing,Y(\ell _{\varnothing }-1))$
form a blue chain of length
$(\varnothing,Y(0)), \ldots, (\varnothing,Y(\ell _{\varnothing }-1))$
form a blue chain of length
![]() $\ell _\varnothing$
and
$\ell _\varnothing$
and
![]() $(2)$
holds as well.
$(2)$
holds as well.
Consider an arbitrary
![]() $X\subseteq{\mathcal{X}}$
and suppose that for all
$X\subseteq{\mathcal{X}}$
and suppose that for all
![]() $X^{\prime}\subset X$
we already defined
$X^{\prime}\subset X$
we already defined
![]() $\ell _{X^{\prime}}$
with Properties (1)−(3). Let
$\ell _{X^{\prime}}$
with Properties (1)−(3). Let
![]() $\ell^{\prime}_X=\max _{\{U\subset X\}} \ell _U$
. Then let
$\ell^{\prime}_X=\max _{\{U\subset X\}} \ell _U$
. Then let
![]() $\ell _X$
be the minimum
$\ell _X$
be the minimum
![]() $\ell$
,
$\ell$
,
![]() $\ell^{\prime}_X\le \ell \le k$
such that
$\ell^{\prime}_X\le \ell \le k$
such that
![]() $(X,Y(\ell ))$
is coloured in red. If there is no such
$(X,Y(\ell ))$
is coloured in red. If there is no such
![]() $\ell$
, then
$\ell$
, then
![]() $\left(X,Y\left(\ell^{\prime}_X\right)\right),\ldots,(X,Y(k))$
is a blue chain of length
$\left(X,Y\left(\ell^{\prime}_X\right)\right),\ldots,(X,Y(k))$
is a blue chain of length
![]() $k-\ell^{\prime}_X+1$
. By definition of
$k-\ell^{\prime}_X+1$
. By definition of
![]() $\ell^{\prime}_X$
there is some
$\ell^{\prime}_X$
there is some
![]() $U\subset X$
with
$U\subset X$
with
![]() $\ell _U=\ell^{\prime}_X$
. In particular,
$\ell _U=\ell^{\prime}_X$
. In particular,
![]() $(2)$
holds for
$(2)$
holds for
![]() $U$
, so there is a blue chain of length
$U$
, so there is a blue chain of length
![]() $\ell^{\prime}_X$
in
$\ell^{\prime}_X$
in
![]() $Q^{U}$
. Note that
$Q^{U}$
. Note that
![]() $(U,Y(\ell _U))\subset \left(X,Y\left(\ell^{\prime}_X\right)\right)$
, so we obtain a blue chain of length
$(U,Y(\ell _U))\subset \left(X,Y\left(\ell^{\prime}_X\right)\right)$
, so we obtain a blue chain of length
![]() $k+1$
. This is a contradiction, thus
$k+1$
. This is a contradiction, thus
![]() $\ell _X$
is well-defined and fulfils Property (3).
$\ell _X$
is well-defined and fulfils Property (3).
If
![]() $\ell _X=\ell^{\prime}_X$
, consider the aforementioned blue chain of length
$\ell _X=\ell^{\prime}_X$
, consider the aforementioned blue chain of length
![]() $\ell^{\prime}_X$
in
$\ell^{\prime}_X$
in
![]() $Q^{U}$
, and otherwise consider this chain together with
$Q^{U}$
, and otherwise consider this chain together with
![]() $\left(X,Y\left(\ell^{\prime}_X\right)\right), \ldots, (X,Y(\ell _X-1))$
. In both cases, we obtain a blue chain of length
$\left(X,Y\left(\ell^{\prime}_X\right)\right), \ldots, (X,Y(\ell _X-1))$
. In both cases, we obtain a blue chain of length
![]() $\ell _X$
, which proves
$\ell _X$
, which proves
![]() $(2)$
. For
$(2)$
. For
![]() $X^{\prime}\subset X\subseteq{\mathcal{X}}$
,
$X^{\prime}\subset X\subseteq{\mathcal{X}}$
,
![]() $\ell _{X^{\prime}}\le \ell^{\prime}_X\le \ell _X$
, thus (1) holds.
$\ell _{X^{\prime}}\le \ell^{\prime}_X\le \ell _X$
, thus (1) holds.
We define
![]() $\phi \,:\,{\mathcal{Q}}({\mathcal{X}})\to Q$
,
$\phi \,:\,{\mathcal{Q}}({\mathcal{X}})\to Q$
,
![]() $\phi (X)=(X,Y(\ell _X))$
. Note that
$\phi (X)=(X,Y(\ell _X))$
. Note that
![]() $\phi (X)\cap{\mathcal{X}}=X$
for every
$\phi (X)\cap{\mathcal{X}}=X$
for every
![]() $X\subseteq{\mathcal{X}}$
and Property (3) implies that
$X\subseteq{\mathcal{X}}$
and Property (3) implies that
![]() $\phi (X)$
is red. Let
$\phi (X)$
is red. Let
![]() $X_1,X_2\subseteq{\mathcal{X}}$
. If
$X_1,X_2\subseteq{\mathcal{X}}$
. If
![]() $\phi (X_1)\subseteq \phi (X_2)$
, it is immediate that
$\phi (X_1)\subseteq \phi (X_2)$
, it is immediate that
![]() $X_1\subseteq X_2$
. Conversely, if
$X_1\subseteq X_2$
. Conversely, if
![]() $X_1\subseteq X_2$
, then by Property (1) we have
$X_1\subseteq X_2$
, then by Property (1) we have
![]() $\ell _{X_1}\le \ell _{X_2}$
. Thus
$\ell _{X_1}\le \ell _{X_2}$
. Thus
![]() $\left(X_1,Y\left(\ell _{X_1}\right)\right)\subseteq \left(X_2,Y\left(\ell _{X_2}\right)\right)$
. As a consequence,
$\left(X_1,Y\left(\ell _{X_1}\right)\right)\subseteq \left(X_2,Y\left(\ell _{X_2}\right)\right)$
. As a consequence,
![]() $\phi$
is an
$\phi$
is an
![]() $\mathcal{X}$
-good embedding of
$\mathcal{X}$
-good embedding of
![]() ${\mathcal{Q}}({\mathcal{X}})$
.
${\mathcal{Q}}({\mathcal{X}})$
.![]()
This Lemma implies the following corollary which is already given in an alternative form by Axenovich and Walzer, see Lemma 4 of [Reference Axenovich and Walzer1].
Corollary 9.
Let
![]() ${\mathcal{X}},{\mathcal{Y}}$
be disjoint sets with
${\mathcal{X}},{\mathcal{Y}}$
be disjoint sets with
![]() $|{\mathcal{X}}|=n$
and
$|{\mathcal{X}}|=n$
and
![]() $|{\mathcal{Y}}|=k$
. Let
$|{\mathcal{Y}}|=k$
. Let
![]() $\mathcal{P}$
be a subposet of a Boolean lattice
$\mathcal{P}$
be a subposet of a Boolean lattice
![]() $Q={\mathcal{Q}}({\mathcal{X}}\cup{\mathcal{Y}})$
such that there is no chain of length
$Q={\mathcal{Q}}({\mathcal{X}}\cup{\mathcal{Y}})$
such that there is no chain of length
![]() $k+1$
in
$k+1$
in
![]() $\mathcal{P}$
. Then there exists a copy of
$\mathcal{P}$
. Then there exists a copy of
![]() $Q_n$
in
$Q_n$
in
![]() $Q$
which contains no vertex of
$Q$
which contains no vertex of
![]() $\mathcal{P}$
.
$\mathcal{P}$
.
Proof. Fix an arbitrary linear ordering of
![]() $\mathcal{Y}$
. Furthermore, let
$\mathcal{Y}$
. Furthermore, let
![]() $c\,:\, Q \to \{blue,red\}$
be the colouring such that
$c\,:\, Q \to \{blue,red\}$
be the colouring such that
 \begin{equation*} c(X) = \begin {cases} \text {blue}, \quad \text { if } X\in {\mathcal {P}},\\ \text {red}, \quad \ \ \text { otherwise.} \end {cases} \end{equation*}
\begin{equation*} c(X) = \begin {cases} \text {blue}, \quad \text { if } X\in {\mathcal {P}},\\ \text {red}, \quad \ \ \text { otherwise.} \end {cases} \end{equation*}
There is no blue chain of length
![]() $k+1$
in
$k+1$
in
![]() $c$
, so by Lemma 8 there is a monochromatic red copy of
$c$
, so by Lemma 8 there is a monochromatic red copy of
![]() $Q_n$
in
$Q_n$
in
![]() $Q$
. This copy does not contain any vertex of
$Q$
. This copy does not contain any vertex of
![]() $\mathcal{P}$
.
$\mathcal{P}$
.![]()
With the help of Lemma 8, we can now prove an upper bound for
![]() $R(Q_2,Q_n)$
. The concluding arguments are due to Grósz, Methuku, and Tompkins [Reference Grósz, Methuku and Tompkins15].
$R(Q_2,Q_n)$
. The concluding arguments are due to Grósz, Methuku, and Tompkins [Reference Grósz, Methuku and Tompkins15].
Proof of Corollary 4. The lower bound follows from Theorem 2. For the upper bound, let
![]() $k\in{\mathbb{N}}$
with
$k\in{\mathbb{N}}$
with
![]() $k=\tfrac{(2+\epsilon )n}{\log (n)}$
. Let
$k=\tfrac{(2+\epsilon )n}{\log (n)}$
. Let
![]() $\mathcal{X}$
and
$\mathcal{X}$
and
![]() $\mathcal{Y}$
be disjoint sets with
$\mathcal{Y}$
be disjoint sets with
![]() $|{\mathcal{X}}|=n$
and
$|{\mathcal{X}}|=n$
and
![]() $|{\mathcal{Y}}|=k$
. Consider a blue/red colouring of
$|{\mathcal{Y}}|=k$
. Consider a blue/red colouring of
![]() $Q={\mathcal{Q}}({\mathcal{X}}\cup{\mathcal{Y}})$
with no monochromatic red copy of
$Q={\mathcal{Q}}({\mathcal{X}}\cup{\mathcal{Y}})$
with no monochromatic red copy of
![]() $Q_n$
. Let
$Q_n$
. Let
![]() $\pi =\left(y_1^\pi,\ldots,y_k^\pi \right)$
be a linear ordering of
$\pi =\left(y_1^\pi,\ldots,y_k^\pi \right)$
be a linear ordering of
![]() $\mathcal{Y}$
. By Lemma 8, there exists a blue chain of length
$\mathcal{Y}$
. By Lemma 8, there exists a blue chain of length
![]() $k+1$
of the form
$k+1$
of the form
![]() $\left(X^\pi _0,\varnothing \right), \left(X^\pi _1,\left\{y^\pi _1\right\}\right),\left(X^\pi _2,\left\{y^\pi _1,y^\pi _2\right\}\right),\ldots, \left(X^\pi _k,{\mathcal{Y}}\right)$
where
$\left(X^\pi _0,\varnothing \right), \left(X^\pi _1,\left\{y^\pi _1\right\}\right),\left(X^\pi _2,\left\{y^\pi _1,y^\pi _2\right\}\right),\ldots, \left(X^\pi _k,{\mathcal{Y}}\right)$
where
![]() $X^\pi _i\subseteq{\mathcal{X}}$
.
$X^\pi _i\subseteq{\mathcal{X}}$
.
Note that there are
![]() $k!$
distinct orderings of
$k!$
distinct orderings of
![]() $\mathcal{Y}$
. For each linear ordering
$\mathcal{Y}$
. For each linear ordering
![]() $\pi$
of
$\pi$
of
![]() $\mathcal{Y}$
we consider
$\mathcal{Y}$
we consider
![]() $X^\pi _0$
and
$X^\pi _0$
and
![]() $X^\pi _k$
, that is the minimal and maximal vertex of the aforementioned chain restricted to
$X^\pi _k$
, that is the minimal and maximal vertex of the aforementioned chain restricted to
![]() $\mathcal{X}$
. By the choice of
$\mathcal{X}$
. By the choice of
![]() $k$
, we obtain
$k$
, we obtain
![]() $k!\gt 2^{2n}$
. In particular by pigeonhole principle, there are distinct
$k!\gt 2^{2n}$
. In particular by pigeonhole principle, there are distinct
![]() $\pi _1,\pi _2$
with
$\pi _1,\pi _2$
with
![]() $X^{\pi _1}_0=X^{\pi _2}_0$
and
$X^{\pi _1}_0=X^{\pi _2}_0$
and
![]() $X^{\pi _1}_k=X^{\pi _2}_k$
. Since
$X^{\pi _1}_k=X^{\pi _2}_k$
. Since
![]() $\pi _1,\pi _2$
are distinct, there exists an index
$\pi _1,\pi _2$
are distinct, there exists an index
![]() $1\le i\le k-1$
with
$1\le i\le k-1$
with
![]() $\left\{y^{\pi _1}_1,\ldots,y^{\pi _1}_i\right\}\neq \left\{y^{\pi _2}_1,\ldots,y^{\pi _2}_i\right\}$
. Then the four vertices
$\left\{y^{\pi _1}_1,\ldots,y^{\pi _1}_i\right\}\neq \left\{y^{\pi _2}_1,\ldots,y^{\pi _2}_i\right\}$
. Then the four vertices
form a blue copy of
![]() $Q_2$
.
$Q_2$
.![]()
2.5. Factorial trees and shrubs
Besides the Boolean lattice, there is another poset which plays a major role in this paper, which we call the factorial tree.
Consider the set of ordered subsets of a fixed non-empty set
![]() $\mathcal{Y}$
, that also could be thought of as a set of strings with non-repeated letters over the alphabet
$\mathcal{Y}$
, that also could be thought of as a set of strings with non-repeated letters over the alphabet
![]() $\mathcal{Y}$
. Note that we also allow the empty set as such an ordered subset. Occasionally, if it is clear from the context, we refer to the empty ordered set
$\mathcal{Y}$
. Note that we also allow the empty set as such an ordered subset. Occasionally, if it is clear from the context, we refer to the empty ordered set
![]() $(\varnothing,\le )$
simply as
$(\varnothing,\le )$
simply as
![]() $\varnothing$
. For an ordered subset
$\varnothing$
. For an ordered subset
![]() $S$
of
$S$
of
![]() $\mathcal{Y}$
, we refer to its underlying unordered set as
$\mathcal{Y}$
, we refer to its underlying unordered set as
![]() $\underline{S}$
. Let
$\underline{S}$
. Let
![]() $|S|=|\underline{S}|$
be the size of
$|S|=|\underline{S}|$
be the size of
![]() $S$
. We also say that
$S$
. We also say that
![]() $S$
is an ordering of
$S$
is an ordering of
![]() $\underline{S}$
.
$\underline{S}$
.
Let
![]() $S$
be an ordered subset of
$S$
be an ordered subset of
![]() $\mathcal{Y}$
. A prefix of
$\mathcal{Y}$
. A prefix of
![]() $S$
is an ordered subset
$S$
is an ordered subset
![]() $T$
of
$T$
of
![]() $\mathcal{Y}$
consisting of the first
$\mathcal{Y}$
consisting of the first
![]() $|T|$
elements of
$|T|$
elements of
![]() $S$
in the ordering induced by
$S$
in the ordering induced by
![]() $S$
. If
$S$
. If
![]() $T$
is a prefix of
$T$
is a prefix of
![]() $S$
, we write
$S$
, we write
![]() $T\le _{\mathcal{O}} S$
. Note that the empty ordered set is a prefix of every ordered set. If
$T\le _{\mathcal{O}} S$
. Note that the empty ordered set is a prefix of every ordered set. If
![]() $T\neq S$
, we say that a prefix
$T\neq S$
, we say that a prefix
![]() $T$
of
$T$
of
![]() $S$
is strict, denoted by
$S$
is strict, denoted by
![]() $T\lt _{\mathcal{O}} S$
. Observe that the prefix relation
$T\lt _{\mathcal{O}} S$
. Observe that the prefix relation
![]() $\le _{\mathcal{O}}$
is transitive, reflexive, and antisymmetric. Let
$\le _{\mathcal{O}}$
is transitive, reflexive, and antisymmetric. Let
![]() ${\mathcal{O}}({\mathcal{Y}})$
be the poset of all ordered subsets of
${\mathcal{O}}({\mathcal{Y}})$
be the poset of all ordered subsets of
![]() $\mathcal{Y}$
equipped with
$\mathcal{Y}$
equipped with
![]() $\le _{\mathcal{O}}$
. We say that this poset is the factorial tree on ground set
$\le _{\mathcal{O}}$
. We say that this poset is the factorial tree on ground set
![]() $\mathcal{Y}$
.
$\mathcal{Y}$
.
In a factorial tree
![]() ${\mathcal{O}}({\mathcal{Y}})$
for every vertex
${\mathcal{O}}({\mathcal{Y}})$
for every vertex
![]() $S\in{\mathcal{O}}({\mathcal{Y}})$
, the set of prefixes
$S\in{\mathcal{O}}({\mathcal{Y}})$
, the set of prefixes
![]() $\{T\in{\mathcal{O}}({\mathcal{Y}})\,:\, T\le _{\mathcal{O}} S\}$
induces a chain. Furthermore, the vertex
$\{T\in{\mathcal{O}}({\mathcal{Y}})\,:\, T\le _{\mathcal{O}} S\}$
induces a chain. Furthermore, the vertex
![]() $\varnothing$
is the unique minimal vertex of
$\varnothing$
is the unique minimal vertex of
![]() $\mathcal{Y}$
, thus
$\mathcal{Y}$
, thus
![]() ${\mathcal{O}}({\mathcal{Y}})$
is an up-tree.
${\mathcal{O}}({\mathcal{Y}})$
is an up-tree.
Let
![]() $\mathcal{X}$
and
$\mathcal{X}$
and
![]() $\mathcal{Y}$
be disjoint sets. Let
$\mathcal{Y}$
be disjoint sets. Let
![]() $Q={\mathcal{Q}}({\mathcal{X}}\cup{\mathcal{Y}})$
and
$Q={\mathcal{Q}}({\mathcal{X}}\cup{\mathcal{Y}})$
and
![]() ${\mathcal{O}}({\mathcal{Y}})$
be the factorial tree with ground set
${\mathcal{O}}({\mathcal{Y}})$
be the factorial tree with ground set
![]() $\mathcal{Y}$
. An embedding
$\mathcal{Y}$
. An embedding
![]() $\tau$
of
$\tau$
of
![]() ${\mathcal{O}}({\mathcal{Y}})$
into
${\mathcal{O}}({\mathcal{Y}})$
into
![]() $Q$
is
$Q$
is
![]() $\mathcal{Y}$
-good if for every
$\mathcal{Y}$
-good if for every
![]() $S\in{\mathcal{O}}({\mathcal{Y}})$
,
$S\in{\mathcal{O}}({\mathcal{Y}})$
,
![]() $\tau (S)\cap{\mathcal{Y}}=\underline{S}$
. We say that a subposet
$\tau (S)\cap{\mathcal{Y}}=\underline{S}$
. We say that a subposet
![]() $\mathcal{P}$
of
$\mathcal{P}$
of
![]() $Q$
is a
$Q$
is a
![]() $\mathcal{Y}$
-good copy of
$\mathcal{Y}$
-good copy of
![]() ${\mathcal{O}}({\mathcal{Y}})$
if there exists a
${\mathcal{O}}({\mathcal{Y}})$
if there exists a
![]() $\mathcal{Y}$
-good embedding
$\mathcal{Y}$
-good embedding
![]() $\tau \,:\,{\mathcal{O}}({\mathcal{Y}}) \to Q$
with image
$\tau \,:\,{\mathcal{O}}({\mathcal{Y}}) \to Q$
with image
![]() $\mathcal{P}$
. We refer to such a copy also as a
$\mathcal{P}$
. We refer to such a copy also as a
![]() $\mathcal{Y}$
-shrub.
$\mathcal{Y}$
-shrub.
Besides that, we also consider a related subposet with slightly weaker conditions. A weak
![]() $\mathcal{Y}$
-shrub is a subposet
$\mathcal{Y}$
-shrub is a subposet
![]() $\mathcal{P}$
of
$\mathcal{P}$
of
![]() $Q$
such that there is a function
$Q$
such that there is a function
![]() $\tau \,:\,{\mathcal{O}}({\mathcal{Y}}) \to Q$
with image
$\tau \,:\,{\mathcal{O}}({\mathcal{Y}}) \to Q$
with image
![]() $\mathcal{P}$
such that for every
$\mathcal{P}$
such that for every
![]() $S\in{\mathcal{O}}({\mathcal{Y}})$
,
$S\in{\mathcal{O}}({\mathcal{Y}})$
,
![]() $\tau (S)\cap{\mathcal{Y}}=\underline{S}$
and for every
$\tau (S)\cap{\mathcal{Y}}=\underline{S}$
and for every
![]() $S,T\in{\mathcal{O}}({\mathcal{Y}})$
with
$S,T\in{\mathcal{O}}({\mathcal{Y}})$
with
![]() $S\lt _{\mathcal{O}} T$
,
$S\lt _{\mathcal{O}} T$
,
![]() $\tau (S)\subset \tau (T)$
. In particular, a weak
$\tau (S)\subset \tau (T)$
. In particular, a weak
![]() $\mathcal{Y}$
-shrub might not correspond to an injective embedding of
$\mathcal{Y}$
-shrub might not correspond to an injective embedding of
![]() ${\mathcal{O}}({\mathcal{Y}})$
.
${\mathcal{O}}({\mathcal{Y}})$
.
Clearly a
![]() $\mathcal{Y}$
-shrub is also a weak
$\mathcal{Y}$
-shrub is also a weak
![]() $\mathcal{Y}$
-shrub. Surprisingly, the converse statement is also true for subposets of a Boolean lattices which do not contain a copy of
$\mathcal{Y}$
-shrub. Surprisingly, the converse statement is also true for subposets of a Boolean lattices which do not contain a copy of
![]() $\Lambda$
.
$\Lambda$
.
Proposition 10.
Let
![]() $\mathcal{X}$
and
$\mathcal{X}$
and
![]() $\mathcal{Y}$
be disjoint sets, let
$\mathcal{Y}$
be disjoint sets, let
![]() $Q={\mathcal{Q}}({\mathcal{X}}\cup{\mathcal{Y}})$
. Let
$Q={\mathcal{Q}}({\mathcal{X}}\cup{\mathcal{Y}})$
. Let
![]() $\mathcal{P}$
be a weak
$\mathcal{P}$
be a weak
![]() $\mathcal{Y}$
-shrub in
$\mathcal{Y}$
-shrub in
![]() $Q$
such that
$Q$
such that
![]() $\mathcal{P}$
contains no copy of
$\mathcal{P}$
contains no copy of
![]() $\Lambda$
. Then
$\Lambda$
. Then
![]() $\mathcal{P}$
is a
$\mathcal{P}$
is a
![]() $\mathcal{Y}$
-shrub.
$\mathcal{Y}$
-shrub.
Proof. Let
![]() $\tau \,:\,{\mathcal{O}}({\mathcal{Y}}) \to Q$
be a map such that for every
$\tau \,:\,{\mathcal{O}}({\mathcal{Y}}) \to Q$
be a map such that for every
![]() $S,T\in{\mathcal{O}}({\mathcal{Y}})$
with
$S,T\in{\mathcal{O}}({\mathcal{Y}})$
with
![]() $S\lt _{\mathcal{O}} T$
, we have
$S\lt _{\mathcal{O}} T$
, we have
![]() $\tau (S)\subset \tau (T)$
and
$\tau (S)\subset \tau (T)$
and
![]() $\tau (S)\cap{\mathcal{Y}}=\underline{S}$
, and let
$\tau (S)\cap{\mathcal{Y}}=\underline{S}$
, and let
![]() $\mathcal{P}$
be its image. For all
$\mathcal{P}$
be its image. For all
![]() $S\in{\mathcal{O}}({\mathcal{Y}})$
, let
$S\in{\mathcal{O}}({\mathcal{Y}})$
, let
![]() $X_S=\tau (S)\cap{\mathcal{X}}$
, that is
$X_S=\tau (S)\cap{\mathcal{X}}$
, that is
![]() $\tau (S)=(X_S,\underline{S})$
. We shall show that
$\tau (S)=(X_S,\underline{S})$
. We shall show that
![]() $\tau$
is an embedding, thus proving that
$\tau$
is an embedding, thus proving that
![]() $\mathcal{P}$
is a
$\mathcal{P}$
is a
![]() $\mathcal{Y}$
-shrub. For that we need to prove that the condition
$\mathcal{Y}$
-shrub. For that we need to prove that the condition
![]() $\tau (S)\subseteq \tau (T)$
implies that
$\tau (S)\subseteq \tau (T)$
implies that
![]() $S\le _{\mathcal{O}} T$
for any ordered subsets
$S\le _{\mathcal{O}} T$
for any ordered subsets
![]() $S$
and
$S$
and
![]() $T$
of
$T$
of
![]() $\mathcal{Y}$
.
$\mathcal{Y}$
.
Let
![]() $\tau (S)\subseteq \tau (T)$
, that is
$\tau (S)\subseteq \tau (T)$
, that is
![]() $(X_S,\underline{S})\subseteq (X_{T},\underline{T})$
. In particular,
$(X_S,\underline{S})\subseteq (X_{T},\underline{T})$
. In particular,
![]() $\underline{S}\subseteq \underline{T}$
and so
$\underline{S}\subseteq \underline{T}$
and so
![]() $|S|\le |T|$
. Let
$|S|\le |T|$
. Let
![]() $R$
be the largest common prefix of
$R$
be the largest common prefix of
![]() $S$
and
$S$
and
![]() $T$
. Such a prefix exists since
$T$
. Such a prefix exists since
![]() $\varnothing$
is a prefix of every ordered set. If
$\varnothing$
is a prefix of every ordered set. If
![]() $|R|=|S|$
, then
$|R|=|S|$
, then
![]() $S=R\le _{\mathcal{O}} T$
and we are done. So we can assume that
$S=R\le _{\mathcal{O}} T$
and we are done. So we can assume that
![]() $|S|\ge |R|+1$
.
$|S|\ge |R|+1$
.
If
![]() $|T|\le |R|+1$
, then
$|T|\le |R|+1$
, then
![]() $|R|+1\le |S|\le |T|\le |R|+1$
. This implies
$|R|+1\le |S|\le |T|\le |R|+1$
. This implies
![]() $|S|=|T|$
and since
$|S|=|T|$
and since
![]() $\underline{S}\subseteq \underline{T}$
, we have
$\underline{S}\subseteq \underline{T}$
, we have
![]() $\underline{S}=\underline{T}$
. Let
$\underline{S}=\underline{T}$
. Let
![]() $\{y\}= \underline{S}\backslash \underline{R}=\underline{T}\backslash \underline{R}$
. Then both
$\{y\}= \underline{S}\backslash \underline{R}=\underline{T}\backslash \underline{R}$
. Then both
![]() $S,T$
have
$S,T$
have
![]() $R$
as prefix of size
$R$
as prefix of size
![]() $|S|-1=|T|-1$
and
$|S|-1=|T|-1$
and
![]() $y$
as final vertex. Thus
$y$
as final vertex. Thus
![]() $S=T$
and we are done as well.
$S=T$
and we are done as well.
From now on, we assume that
![]() $|S|\ge |R|+1$
and
$|S|\ge |R|+1$
and
![]() $|T|\gt |R|+1$
. Consider prefixes
$|T|\gt |R|+1$
. Consider prefixes
![]() $S^{\prime}\le _{\mathcal{O}} S$
and
$S^{\prime}\le _{\mathcal{O}} S$
and
![]() $T^{\prime}\le _{\mathcal{O}} T$
of size
$T^{\prime}\le _{\mathcal{O}} T$
of size
![]() $|R|+1$
. Then
$|R|+1$
. Then
![]() $R$
is a prefix of both
$R$
is a prefix of both
![]() $S^{\prime}$
and
$S^{\prime}$
and
![]() $T^{\prime}$
. Let
$T^{\prime}$
. Let
![]() $y_S$
such that
$y_S$
such that
![]() $\underline{S^{\prime}}\backslash \underline{R}=\{y_S\}$
and let
$\underline{S^{\prime}}\backslash \underline{R}=\{y_S\}$
and let
![]() $y_T$
with
$y_T$
with
![]() $\underline{T^{\prime}}\backslash \underline{R}=\{y_T\}$
.
$\underline{T^{\prime}}\backslash \underline{R}=\{y_T\}$
.
If
![]() $y_S=y_T$
, we obtain
$y_S=y_T$
, we obtain
![]() $S^{\prime}=T^{\prime}$
, which implies that
$S^{\prime}=T^{\prime}$
, which implies that
![]() $R$
is not the largest common prefix of
$R$
is not the largest common prefix of
![]() $S$
and
$S$
and
![]() $T$
, a contradiction.
$T$
, a contradiction.
If
![]() $y_S\neq y_T$
, the unordered sets
$y_S\neq y_T$
, the unordered sets
![]() $\underline{S^{\prime}}$
and
$\underline{S^{\prime}}$
and
![]() $\underline{T^{\prime}}$
are not comparable. In particular,
$\underline{T^{\prime}}$
are not comparable. In particular,
![]() $(X_{T^{\prime}},\underline{T^{\prime}})$
and
$(X_{T^{\prime}},\underline{T^{\prime}})$
and
![]() $(X_{S^{\prime}},\underline{S^{\prime}})$
are incomparable. Because
$(X_{S^{\prime}},\underline{S^{\prime}})$
are incomparable. Because
![]() $S^{\prime}\le _{\mathcal{O}} S$
,
$S^{\prime}\le _{\mathcal{O}} S$
,
![]() $T^{\prime}\lt _{\mathcal{O}} T$
and by our initial assumption, we know that
$T^{\prime}\lt _{\mathcal{O}} T$
and by our initial assumption, we know that
![]() $(X_{S^{\prime}},\underline{S^{\prime}})\subseteq (X_S,\underline{S})\subseteq (X_{T},\underline{T})$
and
$(X_{S^{\prime}},\underline{S^{\prime}})\subseteq (X_S,\underline{S})\subseteq (X_{T},\underline{T})$
and
![]() $(X_{T^{\prime}},\underline{T^{\prime}})\subseteq (X_{T},\underline{T})$
. Since
$(X_{T^{\prime}},\underline{T^{\prime}})\subseteq (X_{T},\underline{T})$
. Since
![]() $|S^{\prime}|=|T^{\prime}|=|R|+1\lt |T|$
, we obtain that both
$|S^{\prime}|=|T^{\prime}|=|R|+1\lt |T|$
, we obtain that both
![]() $(X_{S^{\prime}},\underline{S^{\prime}})$
and
$(X_{S^{\prime}},\underline{S^{\prime}})$
and
![]() $(X_{T^{\prime}},\underline{T^{\prime}})$
are proper subsets of
$(X_{T^{\prime}},\underline{T^{\prime}})$
are proper subsets of
![]() $(X_{T},\underline{T})$
. Then the three vertices
$(X_{T},\underline{T})$
. Then the three vertices
![]() $(X_{T},\underline{T}), (X_{T^{\prime}},\underline{T^{\prime}})$
and
$(X_{T},\underline{T}), (X_{T^{\prime}},\underline{T^{\prime}})$
and
![]() $(X_{S^{\prime}},\underline{S^{\prime}})$
form a copy of
$(X_{S^{\prime}},\underline{S^{\prime}})$
form a copy of
![]() $\Lambda$
in
$\Lambda$
in
![]() $Q$
, so we reach a contradiction.
$Q$
, so we reach a contradiction.![]()
2.6. Construction of an almost optimal shrub
Let
![]() $\mathcal{Y}$
be a
$\mathcal{Y}$
be a
![]() $k$
-element set. Note that a
$k$
-element set. Note that a
![]() $\mathcal{Y}$
-shrub has
$\mathcal{Y}$
-shrub has
![]() $k!$
maximal vertices corresponding to all permutations of
$k!$
maximal vertices corresponding to all permutations of
![]() $\mathcal{Y}$
. These maximal vertices form an antichain, that is are pairwise incomparable. Sperner’s theorem implies that a ground set of any
$\mathcal{Y}$
. These maximal vertices form an antichain, that is are pairwise incomparable. Sperner’s theorem implies that a ground set of any
![]() $\mathcal{Y}$
-shrub must have size at least
$\mathcal{Y}$
-shrub must have size at least
![]() $q$
, where
$q$
, where
![]() $\binom{q}{\lfloor q/2 \rfloor } \geq k!$
, so
$\binom{q}{\lfloor q/2 \rfloor } \geq k!$
, so
![]() $q\ge k(\log k +\log e) + o(k)$
. Next, we shall construct a
$q\ge k(\log k +\log e) + o(k)$
. Next, we shall construct a
![]() $\mathcal{Y}$
-shrub which is almost optimal in the sense that
$\mathcal{Y}$
-shrub which is almost optimal in the sense that
![]() $\mathcal{Y}$
has ground set of size almost matching the lower bound above.
$\mathcal{Y}$
has ground set of size almost matching the lower bound above.
Proposition 11.
Let
![]() $\mathcal{Y}$
be a
$\mathcal{Y}$
be a
![]() $k$
-element set. Let
$k$
-element set. Let
![]() $A$
be a set disjoint from
$A$
be a set disjoint from
![]() $\mathcal{Y}$
such that
$\mathcal{Y}$
such that
![]() $|A| \geq k \cdot \min \{\log k + \log \log k,11\}$
. Then there is a
$|A| \geq k \cdot \min \{\log k + \log \log k,11\}$
. Then there is a
![]() $\mathcal{Y}$
-shrub in
$\mathcal{Y}$
-shrub in
![]() ${\mathcal{Q}}(A\cup{\mathcal{Y}})$
.
${\mathcal{Q}}(A\cup{\mathcal{Y}})$
.
Proof. Let
![]() ${\mathcal{Y}}=\{y_0, \ldots, y_{k-1}\}$
and let
${\mathcal{Y}}=\{y_0, \ldots, y_{k-1}\}$
and let
![]() $Q={\mathcal{Q}}(A\cup{\mathcal{Y}})$
. We use addition of indices modulo
$Q={\mathcal{Q}}(A\cup{\mathcal{Y}})$
. We use addition of indices modulo
![]() $k$
. Let
$k$
. Let
![]() $A_0, \ldots, A_{k-1}$
be pairwise disjoint subsets of
$A_0, \ldots, A_{k-1}$
be pairwise disjoint subsets of
![]() $A$
such that
$A$
such that
![]() $|A_i|= \ell$
for the smallest integer
$|A_i|= \ell$
for the smallest integer
![]() $\ell$
satisfying
$\ell$
satisfying
![]() $\binom{\ell }{\lfloor \ell/2 \rfloor } \geq k$
. Since
$\binom{\ell }{\lfloor \ell/2 \rfloor } \geq k$
. Since
![]() $\ell \le \log k +\log \log k$
for
$\ell \le \log k +\log \log k$
for
![]() $k\ge 256$
and
$k\ge 256$
and
![]() $\ell \le 11$
for
$\ell \le 11$
for
![]() $k\le 256$
, such subsets
$k\le 256$
, such subsets
![]() $A_i$
’s can be chosen. In each
$A_i$
’s can be chosen. In each
![]() ${\mathcal{Q}}(A_i)$
,
${\mathcal{Q}}(A_i)$
,
![]() $i\in \{0,\ldots, k-1\}$
, the elements of size
$i\in \{0,\ldots, k-1\}$
, the elements of size
![]() $\lfloor \ell/2 \rfloor$
form an antichain of size
$\lfloor \ell/2 \rfloor$
form an antichain of size
![]() $k$
. Let
$k$
. Let
![]() $ \{A_i^j: j\in \{0, \ldots, k-1\} \}$
be this antichain enumerated arbitrarily.
$ \{A_i^j: j\in \{0, \ldots, k-1\} \}$
be this antichain enumerated arbitrarily.
Consider the factorial tree
![]() ${\mathcal{O}}({\mathcal{Y}})$
. We shall construct an embedding
${\mathcal{O}}({\mathcal{Y}})$
. We shall construct an embedding
![]() $\tau$
of
$\tau$
of
![]() ${\mathcal{O}}({\mathcal{Y}})$
into
${\mathcal{O}}({\mathcal{Y}})$
into
![]() $Q$
as follows. Let
$Q$
as follows. Let
![]() $\tau (\varnothing )= \varnothing$
. Consider any non-empty ordered subset of
$\tau (\varnothing )= \varnothing$
. Consider any non-empty ordered subset of
![]() $\mathcal{Y}$
, say
$\mathcal{Y}$
, say
![]() $(y_{i_1}, y_{i_2}, \ldots, y_{i_j})$
,
$(y_{i_1}, y_{i_2}, \ldots, y_{i_j})$
,
![]() $1\leq j\leq k$
. If
$1\leq j\leq k$
. If
![]() $j=1$
, let
$j=1$
, let
![]() $\tau ((y_{i_1}))=A_{i_1}\cup \{y_{i_1}\}$
. If
$\tau ((y_{i_1}))=A_{i_1}\cup \{y_{i_1}\}$
. If
![]() $j\gt 1$
, let
$j\gt 1$
, let
For example for
![]() $k=4$
,
$k=4$
,
![]() $\tau ((y_0, y_1, y_2)) = A_0\cup A_1^1\cup A_2^2 \cup \{y_0, y_1, y_2\}$
,
$\tau ((y_0, y_1, y_2)) = A_0\cup A_1^1\cup A_2^2 \cup \{y_0, y_1, y_2\}$
,
![]() $\tau ((y_2, y_3, y_1)) = A_2 \cup A_3^3 \cup A_0^1 \cup \{y_1, y_2, y_3\}$
, and
$\tau ((y_2, y_3, y_1)) = A_2 \cup A_3^3 \cup A_0^1 \cup \{y_1, y_2, y_3\}$
, and
![]() $\tau ((y_3, y_1)) = A_3 \cup A_0^1 \cup \{y_1, y_3\}$
.
$\tau ((y_3, y_1)) = A_3 \cup A_0^1 \cup \{y_1, y_3\}$
.
Note that the image of
![]() ${\mathcal{O}}({\mathcal{Y}})$
under
${\mathcal{O}}({\mathcal{Y}})$
under
![]() $\tau$
is an up-tree,
$\tau$
is an up-tree,
![]() $\mathcal{T}$
, whose minimum vertex is
$\mathcal{T}$
, whose minimum vertex is
![]() $\varnothing$
, see Figures 1 and 2. We see that each maximum vertex of
$\varnothing$
, see Figures 1 and 2. We see that each maximum vertex of
![]() $\mathcal{T}$
is joined to
$\mathcal{T}$
is joined to
![]() $\varnothing$
by a unique chain, a maximal chain. Furthermore, non-zero vertices that belong to distinct maximal chains are incomparable. Observe that
$\varnothing$
by a unique chain, a maximal chain. Furthermore, non-zero vertices that belong to distinct maximal chains are incomparable. Observe that
![]() $\tau$
is a
$\tau$
is a
![]() $\mathcal{Y}$
-good embedding of
$\mathcal{Y}$
-good embedding of
![]() ${\mathcal{O}}({\mathcal{Y}})$
into
${\mathcal{O}}({\mathcal{Y}})$
into
![]() $Q$
. Indeed, for any ordered sequence of distinct vertices
$Q$
. Indeed, for any ordered sequence of distinct vertices
![]() $\big(y_{i_1}, \ldots, y_{i_j}\big)$
, we have
$\big(y_{i_1}, \ldots, y_{i_j}\big)$
, we have
![]() $\tau \big( \big(y_{i_1}, \ldots, y_{i_j}\big)\big)\cap{\mathcal{Y}} = \{y_{i_1}, \ldots, y_{i_j}\}$
. In addition
$\tau \big( \big(y_{i_1}, \ldots, y_{i_j}\big)\big)\cap{\mathcal{Y}} = \{y_{i_1}, \ldots, y_{i_j}\}$
. In addition
![]() $\big(y_{i_1}, \ldots, y_{i_q}\big)\lt _{{\mathcal{O}}} \big(y_{i_1}, \ldots, y_{i_p}\big)$
if and only if
$\big(y_{i_1}, \ldots, y_{i_q}\big)\lt _{{\mathcal{O}}} \big(y_{i_1}, \ldots, y_{i_p}\big)$
if and only if
![]() $\tau \big(\big(y_{i_1}, \ldots, y_{i_q}\big)\big)$
and
$\tau \big(\big(y_{i_1}, \ldots, y_{i_q}\big)\big)$
and
![]() $\tau \big(\big(y_{i_1}, \ldots, y_{i_p}\big)\big)$
are in the same maximal chain of
$\tau \big(\big(y_{i_1}, \ldots, y_{i_p}\big)\big)$
are in the same maximal chain of
![]() $T$
in the corresponding order.
$T$
in the corresponding order.![]()

Figure 1. A diagram illustrating how the
![]() $A_i^j$
’s are being assigned to the elements of the
$A_i^j$
’s are being assigned to the elements of the
![]() $\{y_0, y_1, y_2, y_3\}$
-shrub constructed in Proposition 11.
$\{y_0, y_1, y_2, y_3\}$
-shrub constructed in Proposition 11.

Figure 2. Segment of a shrub highlighted in Figure 1. Here the union signs are omitted because of the spacing, for example
![]() $A_2 A_3^1 A_0^0 y_2 y_1 y_0$
corresponds to the shrub vertex
$A_2 A_3^1 A_0^0 y_2 y_1 y_0$
corresponds to the shrub vertex
![]() $A_2 \cup A_3^1 \cup A_0^0\cup \{ y_2, y_1, y_0\}$
.
$A_2 \cup A_3^1 \cup A_0^0\cup \{ y_2, y_1, y_0\}$
.
3. Duality theorem
In this section, we show a duality statement which is the key argument for the proof of Theorem 3. Recall the following definitions. We call an embedding
![]() $\phi$
of
$\phi$
of
![]() ${\mathcal{Q}}({\mathcal{X}})$
into
${\mathcal{Q}}({\mathcal{X}})$
into
![]() ${\mathcal{Q}}({\mathcal{X}}\cup{\mathcal{Y}})$
for disjoint
${\mathcal{Q}}({\mathcal{X}}\cup{\mathcal{Y}})$
for disjoint
![]() $\mathcal{X}$
and
$\mathcal{X}$
and
![]() $\mathcal{Y}$
,
$\mathcal{Y}$
,
![]() $\mathcal{X}$
-good if
$\mathcal{X}$
-good if
![]() $\phi (X)\cap{\mathcal{X}} = X$
for all
$\phi (X)\cap{\mathcal{X}} = X$
for all
![]() $X\subseteq{\mathcal{X}}$
. We also call a copy of
$X\subseteq{\mathcal{X}}$
. We also call a copy of
![]() ${\mathcal{Q}}({\mathcal{X}})$
in
${\mathcal{Q}}({\mathcal{X}})$
in
![]() ${\mathcal{Q}}({\mathcal{X}}\cup{\mathcal{Y}})$
${\mathcal{Q}}({\mathcal{X}}\cup{\mathcal{Y}})$
![]() $\mathcal{X}$
-good if there is an
$\mathcal{X}$
-good if there is an
![]() $\mathcal{X}$
-good embedding of
$\mathcal{X}$
-good embedding of
![]() ${\mathcal{Q}}({\mathcal{X}})$
into
${\mathcal{Q}}({\mathcal{X}})$
into
![]() ${\mathcal{Q}}({\mathcal{X}}\cup{\mathcal{Y}})$
. An embedding
${\mathcal{Q}}({\mathcal{X}}\cup{\mathcal{Y}})$
. An embedding
![]() $\tau$
of
$\tau$
of
![]() ${\mathcal{O}}({\mathcal{Y}})$
into
${\mathcal{O}}({\mathcal{Y}})$
into
![]() ${\mathcal{Q}}({\mathcal{X}}\cup{\mathcal{Y}})$
is
${\mathcal{Q}}({\mathcal{X}}\cup{\mathcal{Y}})$
is
![]() $\mathcal{Y}$
-good if
$\mathcal{Y}$
-good if
![]() $\tau (S)\cap{\mathcal{Y}}=\underline{S}$
for all
$\tau (S)\cap{\mathcal{Y}}=\underline{S}$
for all
![]() $S\in{\mathcal{O}}({\mathcal{Y}})$
. We say that a copy of
$S\in{\mathcal{O}}({\mathcal{Y}})$
. We say that a copy of
![]() ${\mathcal{O}}({\mathcal{Y}})$
is a
${\mathcal{O}}({\mathcal{Y}})$
is a
![]() $\mathcal{Y}$
-shrub if there exists a
$\mathcal{Y}$
-shrub if there exists a
![]() $\mathcal{Y}$
-good embedding of
$\mathcal{Y}$
-good embedding of
![]() ${\mathcal{O}}({\mathcal{Y}})$
into
${\mathcal{O}}({\mathcal{Y}})$
into
![]() ${\mathcal{Q}}({\mathcal{X}}\cup{\mathcal{Y}})$
.
${\mathcal{Q}}({\mathcal{X}}\cup{\mathcal{Y}})$
.
Theorem 12.
(Duality Theorem) For two disjoint sets
![]() $\mathcal{X}$
and
$\mathcal{X}$
and
![]() $\mathcal{Y}$
, let
$\mathcal{Y}$
, let
![]() $Q={\mathcal{Q}}({\mathcal{X}}\cup{\mathcal{Y}})$
be a blue/red coloured Boolean lattice which contains no blue copy of
$Q={\mathcal{Q}}({\mathcal{X}}\cup{\mathcal{Y}})$
be a blue/red coloured Boolean lattice which contains no blue copy of
![]() $\Lambda$
. Then there is exactly one of the following in
$\Lambda$
. Then there is exactly one of the following in
![]() $Q$
:
$Q$
:
-
a red
 $\mathcal{X}$
-good copy of
$\mathcal{X}$
-good copy of
 ${\mathcal{Q}}({\mathcal{X}})$
, or
${\mathcal{Q}}({\mathcal{X}})$
, or
-
a blue
 $\mathcal{Y}$
-good copy of
$\mathcal{Y}$
-good copy of
 ${\mathcal{O}}({\mathcal{Y}})$
, that is a blue
${\mathcal{O}}({\mathcal{Y}})$
, that is a blue
 $\mathcal{Y}$
-shrub.
$\mathcal{Y}$
-shrub.
Informally speaking, this duality statement claims that for any bipartition
![]() ${\mathcal{X}}\cup{\mathcal{Y}}$
of the ground set of a Boolean lattice there exists either a red copy of
${\mathcal{X}}\cup{\mathcal{Y}}$
of the ground set of a Boolean lattice there exists either a red copy of
![]() ${\mathcal{Q}}({\mathcal{X}})$
that is restricted to
${\mathcal{Q}}({\mathcal{X}})$
that is restricted to
![]() $\mathcal{X}$
or a blue copy of the factorial tree
$\mathcal{X}$
or a blue copy of the factorial tree
![]() ${\mathcal{O}}({\mathcal{Y}})$
restricted to
${\mathcal{O}}({\mathcal{Y}})$
restricted to
![]() $\mathcal{Y}$
. This result can be seen as a strengthening of Lemma 8 in the special case when we forbid a blue copy of
$\mathcal{Y}$
. This result can be seen as a strengthening of Lemma 8 in the special case when we forbid a blue copy of
![]() $\Lambda$
. The Duality Theorem implies a criterion for blue/red coloured Boolean lattices
$\Lambda$
. The Duality Theorem implies a criterion for blue/red coloured Boolean lattices
![]() $Q$
to have neither a blue copy of
$Q$
to have neither a blue copy of
![]() $\Lambda$
nor a red copy of
$\Lambda$
nor a red copy of
![]() $Q_n$
.
$Q_n$
.
Corollary 13.
Let
![]() $n,k\in{\mathbb{N}}$
and
$n,k\in{\mathbb{N}}$
and
![]() $N=n+k$
. Let
$N=n+k$
. Let
![]() $Q={\mathcal{Q}}([N])$
be a blue/red coloured Boolean lattice with no blue copy of
$Q={\mathcal{Q}}([N])$
be a blue/red coloured Boolean lattice with no blue copy of
![]() $\Lambda$
. There is no red copy of
$\Lambda$
. There is no red copy of
![]() $Q_n$
in
$Q_n$
in
![]() $Q$
if and only if for every
$Q$
if and only if for every
![]() ${\mathcal{Y}}\in \binom{[N]}{k}$
there exists a blue
${\mathcal{Y}}\in \binom{[N]}{k}$
there exists a blue
![]() $\mathcal{Y}$
-shrub in
$\mathcal{Y}$
-shrub in
![]() $Q$
.
$Q$
.
Proof. Lemma 7 provides that there is a red copy of
![]() $Q_n$
in
$Q_n$
in
![]() $Q$
if and only if there exists a partition
$Q$
if and only if there exists a partition
![]() $[N]={\mathcal{X}}\cup{\mathcal{Y}}$
of the ground set of
$[N]={\mathcal{X}}\cup{\mathcal{Y}}$
of the ground set of
![]() $Q$
with
$Q$
with
![]() $|{\mathcal{X}}|=n$
and
$|{\mathcal{X}}|=n$
and
![]() $|{\mathcal{Y}}|=k$
as well as an
$|{\mathcal{Y}}|=k$
as well as an
![]() $\mathcal{X}$
-good embedding
$\mathcal{X}$
-good embedding
![]() $\phi$
of
$\phi$
of
![]() $Q({\mathcal{X}})$
into
$Q({\mathcal{X}})$
into
![]() $Q$
with a monochromatic red image.
$Q$
with a monochromatic red image.
If there is a red copy of
![]() $Q_n$
in
$Q_n$
in
![]() $Q$
, then for
$Q$
, then for
![]() ${\mathcal{X}},{\mathcal{Y}}$
from Lemma 7 there is also an
${\mathcal{X}},{\mathcal{Y}}$
from Lemma 7 there is also an
![]() $\mathcal{X}$
-good copy of
$\mathcal{X}$
-good copy of
![]() ${\mathcal{Q}}({\mathcal{X}})$
. Thus by Theorem 12 there is no blue
${\mathcal{Q}}({\mathcal{X}})$
. Thus by Theorem 12 there is no blue
![]() $\mathcal{Y}$
-shrub.
$\mathcal{Y}$
-shrub.
On the other hand, if there is no red copy of
![]() $Q_n$
in
$Q_n$
in
![]() $Q$
, there is no red
$Q$
, there is no red
![]() $\mathcal{X}$
-good copy of
$\mathcal{X}$
-good copy of
![]() ${\mathcal{Q}}({\mathcal{X}})$
for any
${\mathcal{Q}}({\mathcal{X}})$
for any
![]() ${\mathcal{X}} \in \binom{[N]}{n}$
. Then for an arbitrary
${\mathcal{X}} \in \binom{[N]}{n}$
. Then for an arbitrary
![]() $n$
-element subset
$n$
-element subset
![]() $\mathcal{X}$
of
$\mathcal{X}$
of
![]() $[N]$
, let
$[N]$
, let
![]() ${\mathcal{Y}}= [N]\setminus{\mathcal{X}}$
. Now Theorem 12 implies that there exists a blue
${\mathcal{Y}}= [N]\setminus{\mathcal{X}}$
. Now Theorem 12 implies that there exists a blue
![]() $\mathcal{Y}$
-shrub. In particular, there is a blue
$\mathcal{Y}$
-shrub. In particular, there is a blue
![]() $\mathcal{Y}$
-shrub for any
$\mathcal{Y}$
-shrub for any
![]() $k$
-element subset
$k$
-element subset
![]() $\mathcal{Y}$
of
$\mathcal{Y}$
of
![]() $[N]$
.
$[N]$
.![]()
Throughout the section, let
![]() $\mathcal{X}$
and
$\mathcal{X}$
and
![]() $\mathcal{Y}$
be fixed disjoint sets. Let
$\mathcal{Y}$
be fixed disjoint sets. Let
![]() $Q={\mathcal{Q}}({\mathcal{X}}\cup{\mathcal{Y}})$
be a Boolean lattice on ground set
$Q={\mathcal{Q}}({\mathcal{X}}\cup{\mathcal{Y}})$
be a Boolean lattice on ground set
![]() ${\mathcal{X}}\cup{\mathcal{Y}}$
. We fix an arbitrary blue/red colouring of
${\mathcal{X}}\cup{\mathcal{Y}}$
. We fix an arbitrary blue/red colouring of
![]() $Q$
with no blue copy of
$Q$
with no blue copy of
![]() $\Lambda$
. We always let
$\Lambda$
. We always let
![]() $n,k\in{\mathbb{N}}$
such that
$n,k\in{\mathbb{N}}$
such that
![]() $|{\mathcal{X}}|=n$
,
$|{\mathcal{X}}|=n$
,
![]() $|{\mathcal{Y}}|=k$
and let
$|{\mathcal{Y}}|=k$
and let
![]() $N=n+k$
. For
$N=n+k$
. For
![]() $X\subseteq{\mathcal{X}}$
,
$X\subseteq{\mathcal{X}}$
,
![]() $Y\subseteq{\mathcal{Y}}$
, we usually denote the vertex
$Y\subseteq{\mathcal{Y}}$
, we usually denote the vertex
![]() $X\cup Y$
by
$X\cup Y$
by
![]() $(X,Y)$
.
$(X,Y)$
.
In order to characterise colourings of
![]() $Q$
which do not contain an embedding
$Q$
which do not contain an embedding
![]() $\phi$
of
$\phi$
of
![]() ${\mathcal{Q}}({\mathcal{X}})$
into
${\mathcal{Q}}({\mathcal{X}})$
into
![]() $Q$
such that for every
$Q$
such that for every
![]() $X\in{\mathcal{Q}}({\mathcal{X}})$
,
$X\in{\mathcal{Q}}({\mathcal{X}})$
,
![]() $\phi (X)$
is red and
$\phi (X)$
is red and
![]() $\phi (X)\cap{\mathcal{X}}=X$
, we introduce the following notation.
$\phi (X)\cap{\mathcal{X}}=X$
, we introduce the following notation.
For
![]() $X\subseteq{\mathcal{X}}$
and
$X\subseteq{\mathcal{X}}$
and
![]() $Y\subseteq{\mathcal{Y}}$
, we say that the vertex
$Y\subseteq{\mathcal{Y}}$
, we say that the vertex
![]() $(X,Y)\in Q$
is embeddable if there is an embedding
$(X,Y)\in Q$
is embeddable if there is an embedding
![]() $\phi :{\mathcal{Q}}({\mathcal{X}})\cap \{X^{\prime}\subseteq{\mathcal{X}}\,:\, X^{\prime}\supseteq X\}\to Q$
with a monochromatic red image, such that
$\phi :{\mathcal{Q}}({\mathcal{X}})\cap \{X^{\prime}\subseteq{\mathcal{X}}\,:\, X^{\prime}\supseteq X\}\to Q$
with a monochromatic red image, such that
![]() $\phi (X^{\prime})\cap{\mathcal{X}}=X^{\prime}$
for all
$\phi (X^{\prime})\cap{\mathcal{X}}=X^{\prime}$
for all
![]() $X^{\prime}$
and
$X^{\prime}$
and
![]() $\phi (X)\supseteq (X,Y)$
. We say that
$\phi (X)\supseteq (X,Y)$
. We say that
![]() $\phi$
witnesses that
$\phi$
witnesses that
![]() $(X,Y)$
is embeddable.
$(X,Y)$
is embeddable.
This definition immediately implies:
Observation 14.
![]() $(\varnothing,\varnothing )$
is not embeddable if and only if there is no embedding
$(\varnothing,\varnothing )$
is not embeddable if and only if there is no embedding
![]() $\phi \,:\,{\mathcal{Q}}({\mathcal{X}})\to Q$
such that for every
$\phi \,:\,{\mathcal{Q}}({\mathcal{X}})\to Q$
such that for every
![]() $X^{\prime}\subseteq{\mathcal{X}}$
,
$X^{\prime}\subseteq{\mathcal{X}}$
,
![]() $\phi (X^{\prime})$
red and
$\phi (X^{\prime})$
red and
![]() $\phi (X^{\prime})\cap{\mathcal{X}}=X^{\prime}$
.
$\phi (X^{\prime})\cap{\mathcal{X}}=X^{\prime}$
.![]()
The key ingredient for the proof of the Duality Theorem, Theorem 12, is the following characterisation of embeddable vertices.
Lemma 15.
Let
![]() $X\subseteq{\mathcal{X}}$
,
$X\subseteq{\mathcal{X}}$
,
![]() $Y\subseteq{\mathcal{Y}}$
. Let
$Y\subseteq{\mathcal{Y}}$
. Let
![]() $Q={\mathcal{Q}} ({\mathcal{X}}\cup{\mathcal{Y}})$
be a blue/red coloured Boolean lattice with no blue copy of
$Q={\mathcal{Q}} ({\mathcal{X}}\cup{\mathcal{Y}})$
be a blue/red coloured Boolean lattice with no blue copy of
![]() $\Lambda$
. Then
$\Lambda$
. Then
![]() $(X,Y)$
is embeddable if and only if either
$(X,Y)$
is embeddable if and only if either
-
(i)
 $(X,Y)$
is blue and there is a
$(X,Y)$
is blue and there is a
 $Y^{\prime}\subseteq{\mathcal{Y}}$
with
$Y^{\prime}\subseteq{\mathcal{Y}}$
with
 $Y^{\prime}\supset Y$
such that
$Y^{\prime}\supset Y$
such that
 $(X,Y^{\prime})$
is embeddable, or
$(X,Y^{\prime})$
is embeddable, or
-
(ii)
 $(X,Y)$
is red and for all
$(X,Y)$
is red and for all
 $X^{\prime}\subseteq{\mathcal{X}}$
with
$X^{\prime}\subseteq{\mathcal{X}}$
with
 $X^{\prime}\supset X$
,
$X^{\prime}\supset X$
,
 $(X^{\prime},Y)$
is embeddable.
$(X^{\prime},Y)$
is embeddable.
Note that if
![]() $X\subseteq{\mathcal{X}}$
and
$X\subseteq{\mathcal{X}}$
and
![]() $(X,{\mathcal{Y}})$
is blue, then
$(X,{\mathcal{Y}})$
is blue, then
![]() $(X,{\mathcal{Y}})$
is not embeddable.
$(X,{\mathcal{Y}})$
is not embeddable.
Proof. First suppose that
![]() $(X,Y)$
is embeddable. Let
$(X,Y)$
is embeddable. Let
![]() $\phi$
be an embedding of
$\phi$
be an embedding of
![]() ${\mathcal{Q}}({\mathcal{X}})\cap \{X^{\prime}\subseteq{\mathcal{X}}\,:\, X^{\prime}\supseteq X\}$
into
${\mathcal{Q}}({\mathcal{X}})\cap \{X^{\prime}\subseteq{\mathcal{X}}\,:\, X^{\prime}\supseteq X\}$
into
![]() $Q$
witnessing that
$Q$
witnessing that
![]() $(X,Y)$
is embeddable.
$(X,Y)$
is embeddable.
If
![]() $(X,Y)$
is blue, then
$(X,Y)$
is blue, then
![]() $\phi (X)\supset (X,Y)$
because
$\phi (X)\supset (X,Y)$
because
![]() $\phi$
has a monochromatic red image. Thus there exists
$\phi$
has a monochromatic red image. Thus there exists
![]() $Y^{\prime}\subseteq{\mathcal{Y}}$
with
$Y^{\prime}\subseteq{\mathcal{Y}}$
with
![]() $Y^{\prime}\supset Y$
such that
$Y^{\prime}\supset Y$
such that
![]() $\phi (X)=(X,Y^{\prime})$
. But then
$\phi (X)=(X,Y^{\prime})$
. But then
![]() $\phi$
also witnesses that
$\phi$
also witnesses that
![]() $(X,Y^{\prime})$
is embeddable, so Condition (i) is fulfilled.
$(X,Y^{\prime})$
is embeddable, so Condition (i) is fulfilled.
If
![]() $(X,Y)$
is red, pick some arbitrary
$(X,Y)$
is red, pick some arbitrary
![]() $X^*\subseteq{\mathcal{X}}$
such that
$X^*\subseteq{\mathcal{X}}$
such that
![]() $X^*\supset X$
. Then the function
$X^*\supset X$
. Then the function
![]() $\phi ^*\,:\,{\mathcal{Q}}({\mathcal{X}})\cap \{X^{\prime}\subseteq{\mathcal{X}}\,:\, X^{\prime}\supseteq X^*\}\to Q$
,
$\phi ^*\,:\,{\mathcal{Q}}({\mathcal{X}})\cap \{X^{\prime}\subseteq{\mathcal{X}}\,:\, X^{\prime}\supseteq X^*\}\to Q$
,
![]() $\phi ^*(X^{\prime})=\phi (X^{\prime})$
is a restriction of
$\phi ^*(X^{\prime})=\phi (X^{\prime})$
is a restriction of
![]() $\phi$
and therefore an embedding with a monochromatic red image such that
$\phi$
and therefore an embedding with a monochromatic red image such that
![]() $\phi ^*(X^{\prime})\cap{\mathcal{X}}=X^{\prime}$
for all
$\phi ^*(X^{\prime})\cap{\mathcal{X}}=X^{\prime}$
for all
![]() $X^{\prime}$
and
$X^{\prime}$
and
![]() $\phi ^*(X^*)\supseteq (X^*,Y)$
. Thus for every
$\phi ^*(X^*)\supseteq (X^*,Y)$
. Thus for every
![]() $X^*\subseteq{\mathcal{X}}$
with
$X^*\subseteq{\mathcal{X}}$
with
![]() $X^*\supset X$
, the vertex
$X^*\supset X$
, the vertex
![]() $(X^*,Y)$
is embeddable, that is Condition (ii) is fulfilled.
$(X^*,Y)$
is embeddable, that is Condition (ii) is fulfilled.
Now, suppose that Condition (i) or Condition (ii) hold. If (i) holds, then
![]() $(X,Y)$
is blue and there is some
$(X,Y)$
is blue and there is some
![]() $Y^{\prime}\supset Y$
such that
$Y^{\prime}\supset Y$
such that
![]() $(X,Y^{\prime})$
is embeddable. Then the embedding witnessing that also verifies that
$(X,Y^{\prime})$
is embeddable. Then the embedding witnessing that also verifies that
![]() $(X,Y)$
is embeddable.
$(X,Y)$
is embeddable.
For the rest of the proof we assume that (ii) holds, that is that
![]() $(X,Y)$
is red and for any
$(X,Y)$
is red and for any
![]() $X^{\prime}\subseteq{\mathcal{X}}$
with
$X^{\prime}\subseteq{\mathcal{X}}$
with
![]() $X^{\prime}\supset X$
the vertex
$X^{\prime}\supset X$
the vertex
![]() $(X^{\prime},Y)$
is embeddable. We define the required embedding
$(X^{\prime},Y)$
is embeddable. We define the required embedding
![]() $\phi \,:\,{\mathcal{Q}}({\mathcal{X}})\cap \{X^{\prime}\subseteq{\mathcal{X}}\,:\, X^{\prime}\supseteq X\}\to Q$
for every
$\phi \,:\,{\mathcal{Q}}({\mathcal{X}})\cap \{X^{\prime}\subseteq{\mathcal{X}}\,:\, X^{\prime}\supseteq X\}\to Q$
for every
![]() $X^{\prime}$
with
$X^{\prime}$
with
![]() $X\subseteq X^{\prime}\subseteq{\mathcal{X}}$
depending on the number of minimal
$X\subseteq X^{\prime}\subseteq{\mathcal{X}}$
depending on the number of minimal
![]() $X^*$
’s,
$X^*$
’s,
![]() $X\subseteq X^*\subseteq X^{\prime}$
such that
$X\subseteq X^*\subseteq X^{\prime}$
such that
![]() $(X^*,Y)$
is blue as follows. Let
$(X^*,Y)$
is blue as follows. Let
![]() $X^{\prime}$
with
$X^{\prime}$
with
![]() $X\subseteq X^{\prime}\subseteq{\mathcal{X}}$
be arbitrary.
$X\subseteq X^{\prime}\subseteq{\mathcal{X}}$
be arbitrary.
-
(1) If for all
 $X^*$
with
$X^*$
with
 $X\subseteq X^*\subseteq X^{\prime}$
, the vertex
$X\subseteq X^*\subseteq X^{\prime}$
, the vertex
 $(X^*,Y)$
is red, let
$(X^*,Y)$
is red, let
 $\phi (X^{\prime})=(X^{\prime},Y)$
. Note that this case includes
$\phi (X^{\prime})=(X^{\prime},Y)$
. Note that this case includes
 $X^{\prime}=X$
.
$X^{\prime}=X$
. -
(2) If there is a unique minimal
 $X^*$
such that
$X^*$
such that
 $X\subseteq X^*\subseteq X^{\prime}$
and
$X\subseteq X^*\subseteq X^{\prime}$
and
 $(X^*,Y)$
is blue, then
$(X^*,Y)$
is blue, then
 $(X^*,Y)$
is embeddable by Condition (ii). Let
$(X^*,Y)$
is embeddable by Condition (ii). Let
 $\phi _{X^*}$
be an embedding witnessing that. Then set
$\phi _{X^*}$
be an embedding witnessing that. Then set
 $\phi (X^{\prime})=\phi _{X^*}(X^{\prime})$
.
$\phi (X^{\prime})=\phi _{X^*}(X^{\prime})$
. -
(3) Otherwise, let
 $\phi (X^{\prime})=(X^{\prime},{\mathcal{Y}})$
.
$\phi (X^{\prime})=(X^{\prime},{\mathcal{Y}})$
.
Cases (1)-(3) determine a partition of the set
![]() $\{X^{\prime}\subseteq{\mathcal{X}}\,:\, X^{\prime}\supseteq X\}$
into three pairwise disjoint parts. Let
$\{X^{\prime}\subseteq{\mathcal{X}}\,:\, X^{\prime}\supseteq X\}$
into three pairwise disjoint parts. Let
![]() ${\mathcal{M}}_j$
,
${\mathcal{M}}_j$
,
![]() $j\in [3]$
, be the set of those vertices
$j\in [3]$
, be the set of those vertices
![]() $X^{\prime}$
for which
$X^{\prime}$
for which
![]() $\phi$
was assigned in Case (j). Note that
$\phi$
was assigned in Case (j). Note that
![]() ${\mathcal{M}}_1\cup{\mathcal{M}}_2\cup{\mathcal{M}}_3=\{X^{\prime}\subseteq{\mathcal{X}}\,:\, X^{\prime}\supseteq X\}$
.
${\mathcal{M}}_1\cup{\mathcal{M}}_2\cup{\mathcal{M}}_3=\{X^{\prime}\subseteq{\mathcal{X}}\,:\, X^{\prime}\supseteq X\}$
.
Claim 1. The function
![]() $\phi$
witnesses that
$\phi$
witnesses that
![]() $(X,Y)$
is embeddable.
$(X,Y)$
is embeddable.
-
Clearly, for every
 $X^{\prime}\subseteq{\mathcal{X}}$
with
$X^{\prime}\subseteq{\mathcal{X}}$
with
 $X^{\prime}\supseteq X$
,
$X^{\prime}\supseteq X$
,
 $\phi (X^{\prime})\cap{\mathcal{X}}=X^{\prime}$
.
$\phi (X^{\prime})\cap{\mathcal{X}}=X^{\prime}$
. -
 $(X,Y)$
is red, so
$(X,Y)$
is red, so
 $X\in{\mathcal{M}}_1$
. Thus
$X\in{\mathcal{M}}_1$
. Thus
 $\phi (X)=(X,Y)$
.
$\phi (X)=(X,Y)$
. -
The argument verifying that
 $\phi (X^{\prime})$
is red for every
$\phi (X^{\prime})$
is red for every
 $X^{\prime}\subseteq{\mathcal{X}}$
with
$X^{\prime}\subseteq{\mathcal{X}}$
with
 $X^{\prime}\supseteq X$
depends on
$X^{\prime}\supseteq X$
depends on
 $i$
such that
$i$
such that
 $X^{\prime}\in{\mathcal{M}}_i$
. If
$X^{\prime}\in{\mathcal{M}}_i$
. If
 $X^{\prime}\in{\mathcal{M}}_1$
, it is immediate that
$X^{\prime}\in{\mathcal{M}}_1$
, it is immediate that
 $\phi (X^{\prime})$
is red. If
$\phi (X^{\prime})$
is red. If
 $X^{\prime}\in{\mathcal{M}}_2$
,
$X^{\prime}\in{\mathcal{M}}_2$
,
 $\phi _{X^*}$
has a monochromatic red image, thus
$\phi _{X^*}$
has a monochromatic red image, thus
 $\phi (X^{\prime})=\phi _{X^*}(X^{\prime})$
is also red. Now consider the case that
$\phi (X^{\prime})=\phi _{X^*}(X^{\prime})$
is also red. Now consider the case that
 $X^{\prime}\in{\mathcal{M}}_3$
, that is there are
$X^{\prime}\in{\mathcal{M}}_3$
, that is there are
 $X_1,X_2\subseteq{\mathcal{X}}$
with
$X_1,X_2\subseteq{\mathcal{X}}$
with
 $X_1\neq X_2$
and
$X_1\neq X_2$
and
 $X\subseteq X_i\subseteq X^{\prime}$
,
$X\subseteq X_i\subseteq X^{\prime}$
,
 $i\in [2]$
, such that
$i\in [2]$
, such that
 $(X_i,Y)$
are blue and
$(X_i,Y)$
are blue and
 $X_i$
are both minimal with this property. The latter condition implies that
$X_i$
are both minimal with this property. The latter condition implies that
 $X_1$
and
$X_1$
and
 $X_2$
are incomparable, in particular
$X_2$
are incomparable, in particular
 $(X_1,Y)$
and
$(X_1,Y)$
and
 $(X_2,Y)$
are incomparable as well. Moreover, observe that
$(X_2,Y)$
are incomparable as well. Moreover, observe that
 $X_i\neq X^{\prime}$
,
$X_i\neq X^{\prime}$
,
 $i\in [2]$
, because
$i\in [2]$
, because
 $X^{\prime}$
is by definition comparable to both
$X^{\prime}$
is by definition comparable to both
 $X_1$
and
$X_1$
and
 $X_2$
. Now assume for a contradiction that
$X_2$
. Now assume for a contradiction that
 $\phi (X^{\prime})=(X^{\prime},{\mathcal{Y}})$
is blue. Recall that
$\phi (X^{\prime})=(X^{\prime},{\mathcal{Y}})$
is blue. Recall that
 $(X_1,Y)$
and
$(X_1,Y)$
and
 $(X_2,Y)$
are blue. We know that
$(X_2,Y)$
are blue. We know that
 $X_i\subset X^{\prime}$
and
$X_i\subset X^{\prime}$
and
 $Y\subseteq{\mathcal{Y}}$
, thus
$Y\subseteq{\mathcal{Y}}$
, thus
 $(X_i,Y)\subset (X^{\prime},{\mathcal{Y}})$
. As a consequence,
$(X_i,Y)\subset (X^{\prime},{\mathcal{Y}})$
. As a consequence,
 $(X_1,Y)$
,
$(X_1,Y)$
,
 $(X_2,Y)$
, and
$(X_2,Y)$
, and
 $(X^{\prime},{\mathcal{Y}})$
induce a blue copy of
$(X^{\prime},{\mathcal{Y}})$
induce a blue copy of
 $\Lambda$
in
$\Lambda$
in
 $Q$
, which is a contradiction. Thus
$Q$
, which is a contradiction. Thus
 $\phi$
has a monochromatic red image.
$\phi$
has a monochromatic red image. -
It remains to show that
 $\phi$
is an embedding. Let
$\phi$
is an embedding. Let
 $X_1,X_2\subseteq{\mathcal{X}}$
be arbitrary with
$X_1,X_2\subseteq{\mathcal{X}}$
be arbitrary with
 $X\subseteq X_i\subseteq X^{\prime}$
,
$X\subseteq X_i\subseteq X^{\prime}$
,
 $i\in [2]$
. We shall show that
$i\in [2]$
. We shall show that
 $X_1\subseteq X_2$
if and only if
$X_1\subseteq X_2$
if and only if
 $\phi (X_1)\subseteq \phi (X_2)$
. One direction is easy to prove: If
$\phi (X_1)\subseteq \phi (X_2)$
. One direction is easy to prove: If
 $\phi (X_1)\subseteq \phi (X_2)$
, then
$\phi (X_1)\subseteq \phi (X_2)$
, then
 $X_1=\phi (X_1)\cap{\mathcal{X}}\subseteq \phi (X_2)\cap{\mathcal{X}}=X_2$
. Now suppose that
$X_1=\phi (X_1)\cap{\mathcal{X}}\subseteq \phi (X_2)\cap{\mathcal{X}}=X_2$
. Now suppose that
 $X_1\subseteq X_2$
. Let
$X_1\subseteq X_2$
. Let
 $Y_1,Y_2\subseteq{\mathcal{Y}}$
such that
$Y_1,Y_2\subseteq{\mathcal{Y}}$
such that
 $\phi (X_1)=(X_1,Y_1)$
and
$\phi (X_1)=(X_1,Y_1)$
and
 $\phi (X_2)=(X_2,Y_2)$
. Then we shall show that
$\phi (X_2)=(X_2,Y_2)$
. Then we shall show that
 $Y_1\subseteq Y_2$
. Note that
$Y_1\subseteq Y_2$
. Note that
 $Y\subseteq Y_i \subseteq{\mathcal{Y}}$
for
$Y\subseteq Y_i \subseteq{\mathcal{Y}}$
for
 $i\in [2]$
. Assume that at least one of
$i\in [2]$
. Assume that at least one of
 $X_1$
or
$X_1$
or
 $X_2$
is in
$X_2$
is in
 ${\mathcal{M}}_1\cup{\mathcal{M}}_3$
. If
${\mathcal{M}}_1\cup{\mathcal{M}}_3$
. If
 $X_1\in{\mathcal{M}}_1$
, then
$X_1\in{\mathcal{M}}_1$
, then
 $Y_1=Y$
and we are done as
$Y_1=Y$
and we are done as
 $Y\subseteq Y_2$
. Furthermore, if
$Y\subseteq Y_2$
. Furthermore, if
 $X_2\in{\mathcal{M}}_3$
, then
$X_2\in{\mathcal{M}}_3$
, then
 $Y_2={\mathcal{Y}}$
and we are done as well since
$Y_2={\mathcal{Y}}$
and we are done as well since
 $Y_1\subseteq{\mathcal{Y}}$
. If
$Y_1\subseteq{\mathcal{Y}}$
. If
 $X_1\in{\mathcal{M}}_3$
, then
$X_1\in{\mathcal{M}}_3$
, then
 $X_1\subseteq X_2$
implies that
$X_1\subseteq X_2$
implies that
 $X_2$
is also in
$X_2$
is also in
 ${\mathcal{M}}_3$
. Conversely, if
${\mathcal{M}}_3$
. Conversely, if
 $X_2\in{\mathcal{M}}_1$
, the fact that
$X_2\in{\mathcal{M}}_1$
, the fact that
 $X_2\supseteq X_1$
yields that
$X_2\supseteq X_1$
yields that
 $X_1\in{\mathcal{M}}_1$
and we are done as before.
$X_1\in{\mathcal{M}}_1$
and we are done as before.
As a final step, suppose that
![]() $X_1,X_2\in{\mathcal{M}}_2$
. This implies that for each
$X_1,X_2\in{\mathcal{M}}_2$
. This implies that for each
![]() $i\in [2]$
, there is a unique minimal vertex
$i\in [2]$
, there is a unique minimal vertex
![]() $X^*_i$
such that
$X^*_i$
such that
![]() $X\subseteq X^*_i\subseteq X_i$
and
$X\subseteq X^*_i\subseteq X_i$
and
![]() $(X^*_i,Y)$
is blue. Applying the initial assumption,
$(X^*_i,Y)$
is blue. Applying the initial assumption,
![]() $X^*_1\subseteq X_1\subseteq X_2$
. By minimality of
$X^*_1\subseteq X_1\subseteq X_2$
. By minimality of
![]() $X^*_2$
, we obtain that
$X^*_2$
, we obtain that
![]() $X^*_2\subseteq X^*_1$
. Now this provides that
$X^*_2\subseteq X^*_1$
. Now this provides that
![]() $X^*_2\subseteq X^*_1\subseteq X_1$
. Using the minimality of
$X^*_2\subseteq X^*_1\subseteq X_1$
. Using the minimality of
![]() $X^*_1$
, we see that
$X^*_1$
, we see that
![]() $X^*_1\subseteq X^*_2$
, so
$X^*_1\subseteq X^*_2$
, so
![]() $X^*_1=X^*_2$
.
$X^*_1=X^*_2$
.
Recall that
![]() $(X^*_1,Y)=(X^*_2,Y)$
is embeddable since
$(X^*_1,Y)=(X^*_2,Y)$
is embeddable since
![]() $X_1,X_2\in{\mathcal{M}}_2$
. Consider the function
$X_1,X_2\in{\mathcal{M}}_2$
. Consider the function
![]() $\phi _{X^*_1}=\phi _{X^*_2}$
witnessing that. Because
$\phi _{X^*_1}=\phi _{X^*_2}$
witnessing that. Because
![]() $\phi _{X^*_1}$
is an embedding and
$\phi _{X^*_1}$
is an embedding and
![]() $X^*_1\subseteq X_1\subseteq X_2$
, we obtain
$X^*_1\subseteq X_1\subseteq X_2$
, we obtain
![]() $\phi _{X^*_1}(X_1)\subseteq \phi _{X^*_1}(X_2)$
. Combining the given conditions,
$\phi _{X^*_1}(X_1)\subseteq \phi _{X^*_1}(X_2)$
. Combining the given conditions,
that implies that
![]() $Y_1\subseteq Y_2$
.
$Y_1\subseteq Y_2$
.
This concludes the proof of the Claim and the Lemma.
Corollary 16.
Let
![]() $X\subseteq{\mathcal{X}}$
and
$X\subseteq{\mathcal{X}}$
and
![]() $S\in{\mathcal{O}}({\mathcal{Y}})$
such that
$S\in{\mathcal{O}}({\mathcal{Y}})$
such that
![]() $(X,\underline{S})$
is not embeddable. Then there exists some
$(X,\underline{S})$
is not embeddable. Then there exists some
![]() $X^{\prime}\subseteq{\mathcal{X}}$
,
$X^{\prime}\subseteq{\mathcal{X}}$
,
![]() $X^{\prime}\supseteq X$
, such that
$X^{\prime}\supseteq X$
, such that
![]() $(X^{\prime},\underline{S})$
is blue and not embeddable.
$(X^{\prime},\underline{S})$
is blue and not embeddable.
Proof. If
![]() $(X,\underline{S})$
is blue, we are done. Otherwise Lemma 15 yields an
$(X,\underline{S})$
is blue, we are done. Otherwise Lemma 15 yields an
![]() $X_1\subseteq{\mathcal{X}}$
,
$X_1\subseteq{\mathcal{X}}$
,
![]() $X_1\supset X$
such that
$X_1\supset X$
such that
![]() $(X_1,\underline{S})$
is not embeddable. By repeating this argument, we find an
$(X_1,\underline{S})$
is not embeddable. By repeating this argument, we find an
![]() $X^{\prime}\subseteq{\mathcal{X}}$
,
$X^{\prime}\subseteq{\mathcal{X}}$
,
![]() $X^{\prime}\supseteq X$
, with
$X^{\prime}\supseteq X$
, with
![]() $(X^{\prime},\underline{S})$
is blue and not embeddable.
$(X^{\prime},\underline{S})$
is blue and not embeddable.![]()
Next we show a connection between embeddable vertices and the existence of a weak
![]() $\mathcal{Y}$
-shrub. Recall that a weak
$\mathcal{Y}$
-shrub. Recall that a weak
![]() $\mathcal{Y}$
-shrub is a subposet
$\mathcal{Y}$
-shrub is a subposet
![]() $\mathcal{P}$
of
$\mathcal{P}$
of
![]() $Q$
such that there is a function
$Q$
such that there is a function
![]() $\tau :{\mathcal{O}}({\mathcal{Y}}) \to Q$
with image
$\tau :{\mathcal{O}}({\mathcal{Y}}) \to Q$
with image
![]() $\mathcal{P}$
such that for every
$\mathcal{P}$
such that for every
![]() $S\in{\mathcal{O}}({\mathcal{Y}})$
,
$S\in{\mathcal{O}}({\mathcal{Y}})$
,
![]() $\tau (S)\cap{\mathcal{Y}}=\underline{S}$
, and for every
$\tau (S)\cap{\mathcal{Y}}=\underline{S}$
, and for every
![]() $S,T\in{\mathcal{O}}({\mathcal{Y}})$
with
$S,T\in{\mathcal{O}}({\mathcal{Y}})$
with
![]() $S\lt _{\mathcal{O}} T$
,
$S\lt _{\mathcal{O}} T$
,
![]() $\tau (S)\subset \tau (T)$
.
$\tau (S)\subset \tau (T)$
.
Lemma 17.
If
![]() $(\varnothing,\varnothing )$
is not embeddable, then there is a monochromatic blue weak
$(\varnothing,\varnothing )$
is not embeddable, then there is a monochromatic blue weak
![]() $\mathcal{Y}$
-shrub.
$\mathcal{Y}$
-shrub.
Proof. We construct
![]() $\tau \,:\,{\mathcal{O}}({\mathcal{Y}})\to Q$
iteratively and increasingly with respect to the order of
$\tau \,:\,{\mathcal{O}}({\mathcal{Y}})\to Q$
iteratively and increasingly with respect to the order of
![]() ${\mathcal{O}}({\mathcal{Y}})$
. Suppose that
${\mathcal{O}}({\mathcal{Y}})$
. Suppose that
![]() $(\varnothing,\varnothing )$
is not embeddable. By Corollary 16 there is some
$(\varnothing,\varnothing )$
is not embeddable. By Corollary 16 there is some
![]() $X_\varnothing \subseteq{\mathcal{X}}$
such that
$X_\varnothing \subseteq{\mathcal{X}}$
such that
![]() $(X_\varnothing,\varnothing )$
is blue and not embeddable. Let
$(X_\varnothing,\varnothing )$
is blue and not embeddable. Let
![]() $\tau (\varnothing )=(X_\varnothing,\varnothing )$
. From here, we continue iteratively. Suppose that for
$\tau (\varnothing )=(X_\varnothing,\varnothing )$
. From here, we continue iteratively. Suppose that for
![]() $S\in{\mathcal{O}}({\mathcal{Y}})$
,
$S\in{\mathcal{O}}({\mathcal{Y}})$
,
![]() $\underline{S}\neq{\mathcal{Y}}$
, we have defined
$\underline{S}\neq{\mathcal{Y}}$
, we have defined
![]() $X_S\subseteq{\mathcal{X}}$
such that
$X_S\subseteq{\mathcal{X}}$
such that
-
(1)
 $X_S\supseteq X_T$
for every
$X_S\supseteq X_T$
for every
 $T\le _{\mathcal{O}} S$
and
$T\le _{\mathcal{O}} S$
and -
(2)
 $\tau (S)=(X_S,\underline{S})$
is blue and not embeddable.
$\tau (S)=(X_S,\underline{S})$
is blue and not embeddable.
Consider an arbitrary
![]() $S^{\prime}\in{\mathcal{O}}({\mathcal{Y}})$
such that
$S^{\prime}\in{\mathcal{O}}({\mathcal{Y}})$
such that
![]() $S\lt _{\mathcal{O}} S^{\prime}$
and
$S\lt _{\mathcal{O}} S^{\prime}$
and
![]() $|S^{\prime}|=|S|+1$
. By Lemma 15 applied for
$|S^{\prime}|=|S|+1$
. By Lemma 15 applied for
![]() $X_S$
and
$X_S$
and
![]() $\underline{S}$
, we obtain that
$\underline{S}$
, we obtain that
![]() $(X_S,\underline{S^{\prime}})$
is not embeddable. Then Corollary 16 yields that there is some
$(X_S,\underline{S^{\prime}})$
is not embeddable. Then Corollary 16 yields that there is some
![]() $X_{S^{\prime}}\subseteq{\mathcal{X}}$
,
$X_{S^{\prime}}\subseteq{\mathcal{X}}$
,
![]() $X_{S^{\prime}}\supseteq X_S$
, such that
$X_{S^{\prime}}\supseteq X_S$
, such that
![]() $(X_{S^{\prime}},\underline{S^{\prime}})$
is blue and not embeddable. Observe that for
$(X_{S^{\prime}},\underline{S^{\prime}})$
is blue and not embeddable. Observe that for
![]() $T\in{\mathcal{O}}({\mathcal{Y}})$
with
$T\in{\mathcal{O}}({\mathcal{Y}})$
with
![]() $T\le _{\mathcal{O}} S^{\prime}$
, either
$T\le _{\mathcal{O}} S^{\prime}$
, either
![]() $T=S^{\prime}$
and so
$T=S^{\prime}$
and so
![]() $X_T=X_{S^{\prime}}$
, or
$X_T=X_{S^{\prime}}$
, or
![]() $T\le _{\mathcal{O}} S$
and so by
$T\le _{\mathcal{O}} S$
and so by
![]() $(1)$
$(1)$
![]() $X_T\subseteq X_S\subseteq X_{S^{\prime}}$
. Let
$X_T\subseteq X_S\subseteq X_{S^{\prime}}$
. Let
![]() $\tau (S^{\prime})=(X_{S^{\prime}},\underline{S^{\prime}})$
.
$\tau (S^{\prime})=(X_{S^{\prime}},\underline{S^{\prime}})$
.
Using this procedure, we define
![]() $\tau$
for all
$\tau$
for all
![]() $S\in{\mathcal{O}}({\mathcal{Y}})$
. Let
$S\in{\mathcal{O}}({\mathcal{Y}})$
. Let
![]() $\mathcal{P}$
be the subposet of
$\mathcal{P}$
be the subposet of
![]() $Q$
induced by the image of
$Q$
induced by the image of
![]() $\tau$
. We shall show that
$\tau$
. We shall show that
![]() $\mathcal{P}$
is a weak
$\mathcal{P}$
is a weak
![]() $\mathcal{Y}$
-shrub witnessed by the function
$\mathcal{Y}$
-shrub witnessed by the function
![]() $\tau$
. By (2), for every
$\tau$
. By (2), for every
![]() $S\in{\mathcal{O}}({\mathcal{Y}})$
,
$S\in{\mathcal{O}}({\mathcal{Y}})$
,
![]() $\tau (S)$
is blue and
$\tau (S)$
is blue and
![]() $\tau (S)\cap{\mathcal{Y}}=\underline{S}$
.
$\tau (S)\cap{\mathcal{Y}}=\underline{S}$
.
Let
![]() $S,T\in{\mathcal{O}}({\mathcal{Y}})$
with
$S,T\in{\mathcal{O}}({\mathcal{Y}})$
with
![]() $S\lt _{\mathcal{O}} T$
. Let
$S\lt _{\mathcal{O}} T$
. Let
![]() $X_S,X_T\subseteq{\mathcal{X}}$
such that
$X_S,X_T\subseteq{\mathcal{X}}$
such that
![]() $\tau (S)=(X_S,\underline{S})$
and
$\tau (S)=(X_S,\underline{S})$
and
![]() $\tau (T)=(X_T,\underline{T})$
. Clearly,
$\tau (T)=(X_T,\underline{T})$
. Clearly,
![]() $\underline{S}\subset \underline{T}$
. Moreover, item
$\underline{S}\subset \underline{T}$
. Moreover, item
![]() $(1)$
implies that
$(1)$
implies that
![]() $X_S\subseteq X_T$
. Consequently,
$X_S\subseteq X_T$
. Consequently,
![]() $\tau (S)\subset \tau (T)$
.
$\tau (S)\subset \tau (T)$
.![]()
Combining the previously presented Lemmas, we can now prove the Duality Theorem.
Proof of Theorem 12. Let
![]() $\mathcal{X}$
and
$\mathcal{X}$
and
![]() $\mathcal{Y}$
be disjoint sets. Let
$\mathcal{Y}$
be disjoint sets. Let
![]() $Q=Q({\mathcal{X}}\cup{\mathcal{Y}})$
be a blue/red coloured Boolean lattice which contains no blue copy of
$Q=Q({\mathcal{X}}\cup{\mathcal{Y}})$
be a blue/red coloured Boolean lattice which contains no blue copy of
![]() $\Lambda$
.
$\Lambda$
.
First suppose that there is no red
![]() $\mathcal{X}$
-good copy of
$\mathcal{X}$
-good copy of
![]() ${\mathcal{Q}}({\mathcal{X}})$
. By Observation 14,
${\mathcal{Q}}({\mathcal{X}})$
. By Observation 14,
![]() $(\varnothing,\varnothing )$
is not embeddable and Lemma 17 provides that there is a blue weak
$(\varnothing,\varnothing )$
is not embeddable and Lemma 17 provides that there is a blue weak
![]() $\mathcal{Y}$
-shrub in
$\mathcal{Y}$
-shrub in
![]() $Q$
. Using Proposition 10 we obtain a blue
$Q$
. Using Proposition 10 we obtain a blue
![]() $\mathcal{Y}$
-shrub in
$\mathcal{Y}$
-shrub in
![]() $Q$
. This shows that there is either a red
$Q$
. This shows that there is either a red
![]() $\mathcal{X}$
-good copy of
$\mathcal{X}$
-good copy of
![]() ${\mathcal{Q}}({\mathcal{X}})$
or a blue
${\mathcal{Q}}({\mathcal{X}})$
or a blue
![]() $\mathcal{Y}$
-shrub.
$\mathcal{Y}$
-shrub.
Next we show that both events could not happen simultaneously. Let
![]() $n=|{\mathcal{X}}|$
,
$n=|{\mathcal{X}}|$
,
![]() $k=|{\mathcal{Y}}|$
and
$k=|{\mathcal{Y}}|$
and
![]() $N=n+k$
. Assume that there exist both an
$N=n+k$
. Assume that there exist both an
![]() $\mathcal{X}$
-good embedding
$\mathcal{X}$
-good embedding
![]() $\phi \,:\,{\mathcal{Q}}({\mathcal{X}}) \to Q$
with monochromatic red image as well as a
$\phi \,:\,{\mathcal{Q}}({\mathcal{X}}) \to Q$
with monochromatic red image as well as a
![]() $\mathcal{Y}$
-good embedding
$\mathcal{Y}$
-good embedding
![]() $\tau \,:\,{\mathcal{O}}({\mathcal{Y}}) \to Q$
with a monochromatic blue image.
$\tau \,:\,{\mathcal{O}}({\mathcal{Y}}) \to Q$
with a monochromatic blue image.
We apply an iterative argument in order to find a contradiction. Let
![]() $Y_0=\varnothing$
and let
$Y_0=\varnothing$
and let
![]() $S_0=(Y_0,{\le})$
be the empty ordered set. Now let
$S_0=(Y_0,{\le})$
be the empty ordered set. Now let
![]() $X_1\subseteq{\mathcal{X}}$
such that
$X_1\subseteq{\mathcal{X}}$
such that
![]() $\tau (S_0)=(X_1,\underline{S_0})$
and let
$\tau (S_0)=(X_1,\underline{S_0})$
and let
![]() $Y_1\in{\mathcal{Y}}$
such that
$Y_1\in{\mathcal{Y}}$
such that
![]() $\phi (X_1)=(X_1,Y_1)$
. Since
$\phi (X_1)=(X_1,Y_1)$
. Since
![]() $\phi (X_1)$
is red but
$\phi (X_1)$
is red but
![]() $\tau (S_0)$
is blue, we know that
$\tau (S_0)$
is blue, we know that
![]() $\phi (X_1)\neq \tau (S_0)$
and thus
$\phi (X_1)\neq \tau (S_0)$
and thus
![]() $Y_1\neq \underline{S_0}=\varnothing$
, so
$Y_1\neq \underline{S_0}=\varnothing$
, so
![]() $|Y_1|\ge 1$
.
$|Y_1|\ge 1$
.
Now say that we already defined
![]() $X_1,\ldots,X_i$
,
$X_1,\ldots,X_i$
,
![]() $Y_0,\ldots,Y_i$
,
$Y_0,\ldots,Y_i$
,
![]() $S_0,\ldots,S_{i-1}$
for some
$S_0,\ldots,S_{i-1}$
for some
![]() $i\in [k]$
such that
$i\in [k]$
such that
-
 $S_{i-1}\in{\mathcal{O}}$
and
$S_{i-1}\in{\mathcal{O}}$
and
 $\underline{S_{i-1}}=Y_{i-1}$
,
$\underline{S_{i-1}}=Y_{i-1}$
, -
 $\tau (S_{i-1})=(X_i,\underline{S_{i-1}})$
,
$\tau (S_{i-1})=(X_i,\underline{S_{i-1}})$
, -
 $\phi (X_i)=(X_i,Y_i)$
, and
$\phi (X_i)=(X_i,Y_i)$
, and -
 $Y_{i-1}\subset Y_i\subseteq{\mathcal{Y}}$
and
$Y_{i-1}\subset Y_i\subseteq{\mathcal{Y}}$
and
 $|Y_i|\ge i$
.
$|Y_i|\ge i$
.
Fix any ordering
![]() $S_i$
of
$S_i$
of
![]() $Y_i$
such that
$Y_i$
such that
![]() $S_{i-1}\lt _{\mathcal{O}} S_i$
. Such
$S_{i-1}\lt _{\mathcal{O}} S_i$
. Such
![]() $S_i$
exists because
$S_i$
exists because
![]() $\underline{S_{i-1}}=Y_{i-1}\subset Y_i$
.
$\underline{S_{i-1}}=Y_{i-1}\subset Y_i$
.
Then let
![]() $X_{i+1}$
be such that
$X_{i+1}$
be such that
![]() $\tau (S_i)=(X_{i+1},\underline{S_i})$
. Since
$\tau (S_i)=(X_{i+1},\underline{S_i})$
. Since
![]() $S_{i-1}\lt _{\mathcal{O}} S_i$
and
$S_{i-1}\lt _{\mathcal{O}} S_i$
and
![]() $\tau$
is an embedding,
$\tau$
is an embedding,
![]() $(X_{i},\underline{S_{i-1}})=\tau (S_{i-1})\subseteq \tau (S_i)=(X_{i+1},\underline{S_i})$
, therefore
$(X_{i},\underline{S_{i-1}})=\tau (S_{i-1})\subseteq \tau (S_i)=(X_{i+1},\underline{S_i})$
, therefore
![]() $X_i\subseteq X_{i+1}$
. Note that
$X_i\subseteq X_{i+1}$
. Note that
![]() $\phi (X_i)=(X_i,\underline{S_i})$
is coloured red but
$\phi (X_i)=(X_i,\underline{S_i})$
is coloured red but
![]() $\tau (S_i)=(X_{i+1},\underline{S_i})$
is blue. Therefore
$\tau (S_i)=(X_{i+1},\underline{S_i})$
is blue. Therefore
![]() $X_{i}\neq X_{i+1}$
, consequently
$X_{i}\neq X_{i+1}$
, consequently
![]() $X_i\subset X_{i+1}$
and in particular
$X_i\subset X_{i+1}$
and in particular
![]() $\phi (X_i)\subset \phi (X_{i+1})$
because
$\phi (X_i)\subset \phi (X_{i+1})$
because
![]() $\phi$
is an embedding.
$\phi$
is an embedding.
Next let
![]() $Y_{i+1}\subseteq{\mathcal{Y}}$
such that
$Y_{i+1}\subseteq{\mathcal{Y}}$
such that
![]() $\phi (X_{i+1})=(X_{i+1},Y_{i+1})$
. Then
$\phi (X_{i+1})=(X_{i+1},Y_{i+1})$
. Then
![]() $Y_{i+1}\supseteq Y_i$
and furthermore, because
$Y_{i+1}\supseteq Y_i$
and furthermore, because
![]() $(X_{i+1},Y_i)$
is blue but
$(X_{i+1},Y_i)$
is blue but
![]() $\phi (X_{i+1})$
is red,
$\phi (X_{i+1})$
is red,
![]() $Y_{i+1}\neq Y_i$
. Consequently
$Y_{i+1}\neq Y_i$
. Consequently
![]() $Y_{i+1}\supset Y_i$
, and in particular
$Y_{i+1}\supset Y_i$
, and in particular
![]() $|Y_{i+1}|\ge |Y_i|+1\ge i+1$
.
$|Y_{i+1}|\ge |Y_i|+1\ge i+1$
.
Iteratively, we obtain
![]() $Y_{k+1}\subseteq{\mathcal{Y}}$
with
$Y_{k+1}\subseteq{\mathcal{Y}}$
with
![]() $|Y_i|\ge k+1$
, a contradiction to
$|Y_i|\ge k+1$
, a contradiction to
![]() $|{\mathcal{Y}}|=k$
.
$|{\mathcal{Y}}|=k$
.![]()
4. Random colouring with many blue shrubs
We shall provide a colouring that will give us a lower bound on
![]() $R(\Lambda, Q_n)$
. Note that we do not provide an explicit construction but only prove the existence of such a colouring.
$R(\Lambda, Q_n)$
. Note that we do not provide an explicit construction but only prove the existence of such a colouring.
Theorem 18.
Let
![]() $N\in{\mathbb{N}}$
be sufficiently large and
$N\in{\mathbb{N}}$
be sufficiently large and
![]() $k=\frac{10}{216}\frac{N}{\ln (N)}$
. Consider the Boolean lattice
$k=\frac{10}{216}\frac{N}{\ln (N)}$
. Consider the Boolean lattice
![]() $Q={\mathcal{Q}}([N])$
. Then for sufficiently large
$Q={\mathcal{Q}}([N])$
. Then for sufficiently large
![]() $N$
, there exists a blue/red colouring of
$N$
, there exists a blue/red colouring of
![]() $Q$
which contains no blue copy of
$Q$
which contains no blue copy of
![]() $\Lambda$
and such that for each
$\Lambda$
and such that for each
![]() ${\mathcal{Y}}\in \binom{[N]}{k}$
, there is a blue
${\mathcal{Y}}\in \binom{[N]}{k}$
, there is a blue
![]() $\mathcal{Y}$
-shrub in
$\mathcal{Y}$
-shrub in
![]() $Q$
.
$Q$
.
Proof of Theorem 18. Let
![]() $\alpha = 21.6$
and
$\alpha = 21.6$
and
![]() $\beta =0.134$
. Let
$\beta =0.134$
. Let
![]() $N\in{\mathbb{N}}$
and
$N\in{\mathbb{N}}$
and
![]() $k=\frac{1}{\alpha }\frac{N}{\ln (N)}$
, let
$k=\frac{1}{\alpha }\frac{N}{\ln (N)}$
, let
![]() $Q={\mathcal{Q}}([N])$
.
$Q={\mathcal{Q}}([N])$
.
The idea of the proof is to construct a
![]() $\mathcal{Y}$
-shrub, denoted
$\mathcal{Y}$
-shrub, denoted
![]() ${\mathcal{P}}_{{\mathcal{Y}}}$
, for every
${\mathcal{P}}_{{\mathcal{Y}}}$
, for every
![]() ${\mathcal{Y}}\in \binom{[N]}{k}$
, with an additional property so that the selected shrubs are independent. Since each shrub does not contain a copy of
${\mathcal{Y}}\in \binom{[N]}{k}$
, with an additional property so that the selected shrubs are independent. Since each shrub does not contain a copy of
![]() $\Lambda$
, it follows that the independent union of all the
$\Lambda$
, it follows that the independent union of all the
![]() ${\mathcal{P}}_{{\mathcal{Y}}}$
’s also does not contain a copy of
${\mathcal{P}}_{{\mathcal{Y}}}$
’s also does not contain a copy of
![]() $\Lambda$
. We obtain these shrubs by randomly choosing a
$\Lambda$
. We obtain these shrubs by randomly choosing a
![]() $\mathcal{Y}$
-framework for every
$\mathcal{Y}$
-framework for every
![]() ${\mathcal{Y}}\in \binom{[N]}{k}$
and then constructing a
${\mathcal{Y}}\in \binom{[N]}{k}$
and then constructing a
![]() $\mathcal{Y}$
-shrub based on each of them. Afterwards we define a colouring where every vertex in each constructed shrub is coloured blue and the remaining vertices red.
$\mathcal{Y}$
-shrub based on each of them. Afterwards we define a colouring where every vertex in each constructed shrub is coloured blue and the remaining vertices red.
A
![]() $\mathcal{Y}$
-framework of
$\mathcal{Y}$
-framework of
![]() ${\mathcal{Y}}\in \binom{[N]}{k}$
is a
${\mathcal{Y}}\in \binom{[N]}{k}$
is a
![]() $4$
-tuple
$4$
-tuple
![]() $({\mathcal{Y}},A_{\mathcal{Y}},Z_{\mathcal{Y}}, X_{\mathcal{Y}})$
such that
$({\mathcal{Y}},A_{\mathcal{Y}},Z_{\mathcal{Y}}, X_{\mathcal{Y}})$
such that
-
 $\mathcal{Y}$
,
$\mathcal{Y}$
,
 $A_{\mathcal{Y}}$
$A_{\mathcal{Y}}$
 $Z_{\mathcal{Y}}$
are pairwise disjoint and
$Z_{\mathcal{Y}}$
are pairwise disjoint and
 ${\mathcal{Y}}\cup A_{\mathcal{Y}}\cup Z_{\mathcal{Y}}=[N]$
,
${\mathcal{Y}}\cup A_{\mathcal{Y}}\cup Z_{\mathcal{Y}}=[N]$
, -
 $|A_{\mathcal{Y}}|=\tfrac{3}{2}k\ln k-k$
,
$|A_{\mathcal{Y}}|=\tfrac{3}{2}k\ln k-k$
, -
 $X_{\mathcal{Y}}\subseteq Z_{\mathcal{Y}}$
.
$X_{\mathcal{Y}}\subseteq Z_{\mathcal{Y}}$
.
A
![]() $\mathcal{Y}$
-framework is random if
$\mathcal{Y}$
-framework is random if
-
 $A_{\mathcal{Y}}\in \binom{[N]\backslash{\mathcal{Y}}}{\tfrac{3}{2}k\ln k-k}$
is chosen uniformly at random, and
$A_{\mathcal{Y}}\in \binom{[N]\backslash{\mathcal{Y}}}{\tfrac{3}{2}k\ln k-k}$
is chosen uniformly at random, and -
each element of
 $Z_{\mathcal{Y}}=[N]\backslash ({\mathcal{Y}}\cup A_{\mathcal{Y}})$
is included in
$Z_{\mathcal{Y}}=[N]\backslash ({\mathcal{Y}}\cup A_{\mathcal{Y}})$
is included in
 $X_{\mathcal{Y}}$
independently at random with probability
$X_{\mathcal{Y}}$
independently at random with probability
 $\frac{1}{2}$
.
$\frac{1}{2}$
.
Now draw a random
![]() $\mathcal{Y}$
-framework for every
$\mathcal{Y}$
-framework for every
![]() ${\mathcal{Y}}\in \binom{[N]}{k}$
. Observe that by choice of
${\mathcal{Y}}\in \binom{[N]}{k}$
. Observe that by choice of
![]() $k$
,
$k$
,
![]() $k\ln k =\frac{N}{\alpha }\cdot \frac{\ln (N)-\ln (\alpha )-\ln \ln (N)}{\ln (N)}$
, so
$k\ln k =\frac{N}{\alpha }\cdot \frac{\ln (N)-\ln (\alpha )-\ln \ln (N)}{\ln (N)}$
, so
![]() $\frac{20N}{21\alpha } \le k\ln k\le \frac{N}{\alpha }$
. Since
$\frac{20N}{21\alpha } \le k\ln k\le \frac{N}{\alpha }$
. Since
![]() $|Z_{\mathcal{Y}}|= N-\tfrac{3}{2}k\ln k$
, we have
$|Z_{\mathcal{Y}}|= N-\tfrac{3}{2}k\ln k$
, we have
![]() $\left(1-\frac{3}{2\alpha }\right)N\le |Z_{\mathcal{Y}}|\le \left(1-\frac{10}{7\alpha }\right)N$
.
$\left(1-\frac{3}{2\alpha }\right)N\le |Z_{\mathcal{Y}}|\le \left(1-\frac{10}{7\alpha }\right)N$
.
Claim 2. W.h.p. for every
![]() ${\mathcal{Y}}_1,{\mathcal{Y}}_2\in \binom{[N]}{k}$
with
${\mathcal{Y}}_1,{\mathcal{Y}}_2\in \binom{[N]}{k}$
with
![]() ${\mathcal{Y}}_1\neq{\mathcal{Y}}_2$
,
${\mathcal{Y}}_1\neq{\mathcal{Y}}_2$
,
![]() $|X_{{\mathcal{Y}}_1}\cap Z_{{\mathcal{Y}}_2}|\ge \beta N$
.
$|X_{{\mathcal{Y}}_1}\cap Z_{{\mathcal{Y}}_2}|\ge \beta N$
.
Consider some arbitrary
![]() ${\mathcal{Y}}_1,{\mathcal{Y}}_2\in \binom{[N]}{k}$
,
${\mathcal{Y}}_1,{\mathcal{Y}}_2\in \binom{[N]}{k}$
,
![]() ${\mathcal{Y}}_1\neq{\mathcal{Y}}_2$
. Observe that
${\mathcal{Y}}_1\neq{\mathcal{Y}}_2$
. Observe that
![]() $\left(1-\frac{3}{\alpha }\right)N\le |Z_{{\mathcal{Y}}_1}\cap Z_{{\mathcal{Y}}_2}|\le |Z_{\mathcal{Y}}|\le \left(1-\frac{10}{7\alpha }\right)N$
. In a random
$\left(1-\frac{3}{\alpha }\right)N\le |Z_{{\mathcal{Y}}_1}\cap Z_{{\mathcal{Y}}_2}|\le |Z_{\mathcal{Y}}|\le \left(1-\frac{10}{7\alpha }\right)N$
. In a random
![]() $\mathcal{Y}$
-framework, each element of
$\mathcal{Y}$
-framework, each element of
![]() $Z_{{\mathcal{Y}}_1}\cap Z_{{\mathcal{Y}}_2}$
is contained in
$Z_{{\mathcal{Y}}_1}\cap Z_{{\mathcal{Y}}_2}$
is contained in
![]() $X_{{\mathcal{Y}}_1}\cap Z_{{\mathcal{Y}}_2}$
independently with probability
$X_{{\mathcal{Y}}_1}\cap Z_{{\mathcal{Y}}_2}$
independently with probability
![]() $\frac 12$
. Consequently,
$\frac 12$
. Consequently,
![]() $|X_{{\mathcal{Y}}_1}\cap Z_{{\mathcal{Y}}_1}|\sim \text{Bin}\left(|Z_{{\mathcal{Y}}_1}\cap Z_{{\mathcal{Y}}_2}|,\frac 12\right)$
and
$|X_{{\mathcal{Y}}_1}\cap Z_{{\mathcal{Y}}_1}|\sim \text{Bin}\left(|Z_{{\mathcal{Y}}_1}\cap Z_{{\mathcal{Y}}_2}|,\frac 12\right)$
and
![]() ${\mathbb{E}}\left(|X_{{\mathcal{Y}}_1}\cap Z_{{\mathcal{Y}}_1}|\right)=\frac 12 |Z_{{\mathcal{Y}}_1}\cap Z_{{\mathcal{Y}}_2}|$
. We have
${\mathbb{E}}\left(|X_{{\mathcal{Y}}_1}\cap Z_{{\mathcal{Y}}_1}|\right)=\frac 12 |Z_{{\mathcal{Y}}_1}\cap Z_{{\mathcal{Y}}_2}|$
. We have
![]() $1-\frac 3\alpha \ge 2\beta$
. In addition,
$1-\frac 3\alpha \ge 2\beta$
. In addition,
![]() $\frac{\big (\frac{1}{2}-\frac{3}{2\alpha }-\beta \big )^2}{1-\frac{10}{7\alpha }}\gt \frac{2}{\alpha }$
, thus there exist some
$\frac{\big (\frac{1}{2}-\frac{3}{2\alpha }-\beta \big )^2}{1-\frac{10}{7\alpha }}\gt \frac{2}{\alpha }$
, thus there exist some
![]() $\epsilon \gt 0$
such that
$\epsilon \gt 0$
such that
![]() $\frac{\big (\frac{1}{2}-\frac{3}{2\alpha }-\beta \big )^2}{1-\frac{10}{7\alpha }}\geq \epsilon + \frac{2}{\alpha }$
. Applying Chernoff’s inequality gives
$\frac{\big (\frac{1}{2}-\frac{3}{2\alpha }-\beta \big )^2}{1-\frac{10}{7\alpha }}\geq \epsilon + \frac{2}{\alpha }$
. Applying Chernoff’s inequality gives
 \begin{eqnarray*}{\mathbb{P}}\left(|X_{{\mathcal{Y}}_1}\cap Z_{{\mathcal{Y}}_2}|\le \beta N\right)&=&{\mathbb{P}}\left (|X_{{\mathcal{Y}}_1}\cap Z_{{\mathcal{Y}}_2}|\le \frac{|Z_{{\mathcal{Y}}_1}\cap Z_{{\mathcal{Y}}_2}|}{2}-\left (\frac{|Z_{{\mathcal{Y}}_1}\cap Z_{{\mathcal{Y}}_2}|}{2}-\beta N\right )\right )\\ &\le & \exp \left ({-}\frac{\Big (\frac{|Z_{{\mathcal{Y}}_1}\cap Z_{{\mathcal{Y}}_2}|}{2}-\beta N\Big )^2}{|Z_{{\mathcal{Y}}_1}\cap Z_{{\mathcal{Y}}_2}|}\right )\\ &\le & \exp \left ({-}\frac{\left(\left(\frac{1}{2}-\frac{3}{2\alpha }\right)-\beta \right)^2}{(1-\frac{10}{7\alpha })}\cdot N\right )\\ &\le & \exp \left ({-}\left (\frac{2}{\alpha }+\epsilon \right )\cdot N\right ). \end{eqnarray*}
\begin{eqnarray*}{\mathbb{P}}\left(|X_{{\mathcal{Y}}_1}\cap Z_{{\mathcal{Y}}_2}|\le \beta N\right)&=&{\mathbb{P}}\left (|X_{{\mathcal{Y}}_1}\cap Z_{{\mathcal{Y}}_2}|\le \frac{|Z_{{\mathcal{Y}}_1}\cap Z_{{\mathcal{Y}}_2}|}{2}-\left (\frac{|Z_{{\mathcal{Y}}_1}\cap Z_{{\mathcal{Y}}_2}|}{2}-\beta N\right )\right )\\ &\le & \exp \left ({-}\frac{\Big (\frac{|Z_{{\mathcal{Y}}_1}\cap Z_{{\mathcal{Y}}_2}|}{2}-\beta N\Big )^2}{|Z_{{\mathcal{Y}}_1}\cap Z_{{\mathcal{Y}}_2}|}\right )\\ &\le & \exp \left ({-}\frac{\left(\left(\frac{1}{2}-\frac{3}{2\alpha }\right)-\beta \right)^2}{(1-\frac{10}{7\alpha })}\cdot N\right )\\ &\le & \exp \left ({-}\left (\frac{2}{\alpha }+\epsilon \right )\cdot N\right ). \end{eqnarray*}
Let
![]() $E_1$
be the event that for some distinct
$E_1$
be the event that for some distinct
![]() ${\mathcal{Y}}_1,{\mathcal{Y}}_2\in \binom{[N]}{k}$
,
${\mathcal{Y}}_1,{\mathcal{Y}}_2\in \binom{[N]}{k}$
,
![]() $|X_{{\mathcal{Y}}_1}\cap Z_{{\mathcal{Y}}_2}|\le \beta N$
. Then
$|X_{{\mathcal{Y}}_1}\cap Z_{{\mathcal{Y}}_2}|\le \beta N$
. Then
 \begin{eqnarray*}{\mathbb{P}}(E_1)&= & \binom{N}{k}\left (\binom{N}{k}-1\right ){\mathbb{P}}(|X_{{\mathcal{Y}}_1}\cap Z_{{\mathcal{Y}}_2}|\le \beta N)\\ &\le & N^{2k} \exp \left ({-}\left (\frac{2}{\alpha }+\epsilon \right )\cdot N\right )\\ &\le & \exp \left (\frac{2N\ln (N)}{\alpha \ln (N)} - \left (\frac{2}{\alpha }+\epsilon \right )\cdot N\right )\\ &=& \exp ({-}\epsilon N)\to 0, \mbox{ as } N\to \infty . \end{eqnarray*}
\begin{eqnarray*}{\mathbb{P}}(E_1)&= & \binom{N}{k}\left (\binom{N}{k}-1\right ){\mathbb{P}}(|X_{{\mathcal{Y}}_1}\cap Z_{{\mathcal{Y}}_2}|\le \beta N)\\ &\le & N^{2k} \exp \left ({-}\left (\frac{2}{\alpha }+\epsilon \right )\cdot N\right )\\ &\le & \exp \left (\frac{2N\ln (N)}{\alpha \ln (N)} - \left (\frac{2}{\alpha }+\epsilon \right )\cdot N\right )\\ &=& \exp ({-}\epsilon N)\to 0, \mbox{ as } N\to \infty . \end{eqnarray*}
This proves Claim 1.
Claim 3. W.h.p. for every
![]() ${\mathcal{Y}}_1,{\mathcal{Y}}_2\in \binom{[N]}{k}$
with
${\mathcal{Y}}_1,{\mathcal{Y}}_2\in \binom{[N]}{k}$
with
![]() ${\mathcal{Y}}_1\neq{\mathcal{Y}}_2$
,
${\mathcal{Y}}_1\neq{\mathcal{Y}}_2$
,
![]() $X_{{\mathcal{Y}}_1}\cap Z_{{\mathcal{Y}}_2}\not \subseteq X_{{\mathcal{Y}}_2}$
.
$X_{{\mathcal{Y}}_1}\cap Z_{{\mathcal{Y}}_2}\not \subseteq X_{{\mathcal{Y}}_2}$
.
We can suppose that the collection of random frameworks fulfils the property of Claim 1. Let
![]() ${\mathcal{Y}}_1,{\mathcal{Y}}_2\in \binom{[N]}{k}$
be such that
${\mathcal{Y}}_1,{\mathcal{Y}}_2\in \binom{[N]}{k}$
be such that
![]() ${\mathcal{Y}}_1\neq{\mathcal{Y}}_2$
. Note that each element of
${\mathcal{Y}}_1\neq{\mathcal{Y}}_2$
. Note that each element of
![]() $X_{{\mathcal{Y}}_1}\cap Z_{{\mathcal{Y}}_2}$
is contained in
$X_{{\mathcal{Y}}_1}\cap Z_{{\mathcal{Y}}_2}$
is contained in
![]() $X_{{\mathcal{Y}}_2}$
with probability
$X_{{\mathcal{Y}}_2}$
with probability
![]() $\frac{1}{2}$
. Thus,
$\frac{1}{2}$
. Thus,
Let
![]() $E_2$
be the event that there exist
$E_2$
be the event that there exist
![]() ${\mathcal{Y}}_1,{\mathcal{Y}}_2\in \binom{[N]}{k}$
with
${\mathcal{Y}}_1,{\mathcal{Y}}_2\in \binom{[N]}{k}$
with
![]() ${\mathcal{Y}}_1\neq{\mathcal{Y}}_2$
such that
${\mathcal{Y}}_1\neq{\mathcal{Y}}_2$
such that
![]() $X_{{\mathcal{Y}}_1}\cap Z_{{\mathcal{Y}}_2}\not \subseteq X_{{\mathcal{Y}}_2}$
. Since
$X_{{\mathcal{Y}}_1}\cap Z_{{\mathcal{Y}}_2}\not \subseteq X_{{\mathcal{Y}}_2}$
. Since
![]() $\frac{2}{\alpha }\lt \ln (2)\beta$
, we have
$\frac{2}{\alpha }\lt \ln (2)\beta$
, we have
This proves Claim 2.
In particular, there exists a collection of
![]() $\mathcal{Y}$
-frameworks
$\mathcal{Y}$
-frameworks
![]() $({\mathcal{Y}},A_{\mathcal{Y}},Z_{\mathcal{Y}}, X_{\mathcal{Y}})$
,
$({\mathcal{Y}},A_{\mathcal{Y}},Z_{\mathcal{Y}}, X_{\mathcal{Y}})$
,
![]() ${\mathcal{Y}}\in \binom{[N]}{k}$
, such that for every
${\mathcal{Y}}\in \binom{[N]}{k}$
, such that for every
![]() ${\mathcal{Y}}_1,{\mathcal{Y}}_2\in \binom{[N]}{k}$
with
${\mathcal{Y}}_1,{\mathcal{Y}}_2\in \binom{[N]}{k}$
with
![]() ${\mathcal{Y}}_1\neq{\mathcal{Y}}_2$
,
${\mathcal{Y}}_1\neq{\mathcal{Y}}_2$
,
![]() $X_{{\mathcal{Y}}_1}\cap Z_{{\mathcal{Y}}_2}\not \subseteq X_{{\mathcal{Y}}_2}$
.
$X_{{\mathcal{Y}}_1}\cap Z_{{\mathcal{Y}}_2}\not \subseteq X_{{\mathcal{Y}}_2}$
.
Note that
![]() $|A_{{\mathcal{Y}}}|=\tfrac{3}{2}k\ln k-k\ge k(\log k + \log \log k)$
. Let
$|A_{{\mathcal{Y}}}|=\tfrac{3}{2}k\ln k-k\ge k(\log k + \log \log k)$
. Let
![]() ${\mathcal{P}}^{\prime}_{{\mathcal{Y}}}$
be a
${\mathcal{P}}^{\prime}_{{\mathcal{Y}}}$
be a
![]() $\mathcal{Y}$
-shrub in
$\mathcal{Y}$
-shrub in
![]() ${\mathcal{Q}}(A_{{\mathcal{Y}}}\cup{\mathcal{Y}})$
as guaranteed by Lemma 11. Note that
${\mathcal{Q}}(A_{{\mathcal{Y}}}\cup{\mathcal{Y}})$
as guaranteed by Lemma 11. Note that
![]() ${\mathcal{P}}_{{\mathcal{Y}}}$
’s are not necessarily independent. Let
${\mathcal{P}}_{{\mathcal{Y}}}$
’s are not necessarily independent. Let
![]() ${\mathcal{P}}_{{\mathcal{Y}}}$
be obtained from
${\mathcal{P}}_{{\mathcal{Y}}}$
be obtained from
![]() ${\mathcal{P}}^{\prime}_{{\mathcal{Y}}}$
by replacing each vertex
${\mathcal{P}}^{\prime}_{{\mathcal{Y}}}$
by replacing each vertex
![]() $W$
of
$W$
of
![]() ${\mathcal{P}}^{\prime}_{{\mathcal{Y}}}$
with
${\mathcal{P}}^{\prime}_{{\mathcal{Y}}}$
with
![]() $W\cup X_{{\mathcal{Y}}}$
. Then
$W\cup X_{{\mathcal{Y}}}$
. Then
![]() ${\mathcal{P}}_{{\mathcal{Y}}}$
is a
${\mathcal{P}}_{{\mathcal{Y}}}$
is a
![]() $\mathcal{Y}$
-shrub in
$\mathcal{Y}$
-shrub in
![]() $Q$
.
$Q$
.
Claim 4. Let
![]() ${\mathcal{Y}}_1,{\mathcal{Y}}_2$
be two distinct
${\mathcal{Y}}_1,{\mathcal{Y}}_2$
be two distinct
![]() $k$
-element subsets of
$k$
-element subsets of
![]() $[N]$
. Then
$[N]$
. Then
![]() ${\mathcal{P}}_{{\mathcal{Y}}_1}$
and
${\mathcal{P}}_{{\mathcal{Y}}_1}$
and
![]() ${\mathcal{P}}_{{\mathcal{Y}}_2}$
are independent.
${\mathcal{P}}_{{\mathcal{Y}}_2}$
are independent.
Consider arbitrary elements
![]() $U_i\in{\mathcal{P}}_{{\mathcal{Y}}_i}$
,
$U_i\in{\mathcal{P}}_{{\mathcal{Y}}_i}$
,
![]() $i\in [2]$
. Recall that
$i\in [2]$
. Recall that
![]() $X_{{\mathcal{Y}}_1}\cap Z_{{\mathcal{Y}}_2}\not \subseteq X_{{\mathcal{Y}}_2}$
, which implies that there exists some
$X_{{\mathcal{Y}}_1}\cap Z_{{\mathcal{Y}}_2}\not \subseteq X_{{\mathcal{Y}}_2}$
, which implies that there exists some
![]() $z\in (X_{{\mathcal{Y}}_1}\cap Z_{{\mathcal{Y}}_2})\backslash X_{{\mathcal{Y}}_2}$
. Note that
$z\in (X_{{\mathcal{Y}}_1}\cap Z_{{\mathcal{Y}}_2})\backslash X_{{\mathcal{Y}}_2}$
. Note that
![]() $z\in U_1$
since
$z\in U_1$
since
![]() $X_{{\mathcal{Y}}_1}\subseteq U_1$
. Moreover
$X_{{\mathcal{Y}}_1}\subseteq U_1$
. Moreover
![]() $z\not \in U_2$
since
$z\not \in U_2$
since
![]() $z\in Z_{{\mathcal{Y}}_2}\setminus X_{{\mathcal{Y}}_2}$
and
$z\in Z_{{\mathcal{Y}}_2}\setminus X_{{\mathcal{Y}}_2}$
and
![]() $(Z_{{\mathcal{Y}}_2}\setminus X_{{\mathcal{Y}}_2})\cap U_2 = \varnothing$
. In particular,
$(Z_{{\mathcal{Y}}_2}\setminus X_{{\mathcal{Y}}_2})\cap U_2 = \varnothing$
. In particular,
![]() $z\in U_1\backslash U_2$
. Similarly, there is an element
$z\in U_1\backslash U_2$
. Similarly, there is an element
![]() $w\in U_2\backslash U_1$
. Thus
$w\in U_2\backslash U_1$
. Thus
![]() $U_1\not \sim U_2$
.
$U_1\not \sim U_2$
.
We consider the following colouring
![]() $c\,:\, Q\to \{\text{blue, red}\}$
. For
$c\,:\, Q\to \{\text{blue, red}\}$
. For
![]() $X\subseteq [N]$
, let
$X\subseteq [N]$
, let
 \begin{equation*} c(X) = \begin{cases} \text{blue}, \quad \mbox{ if } X\in \bigcup _{{\mathcal{Y}}\in \binom{[N]}{k}}{\mathcal{P}}_{\mathcal{Y}},\\ \text{red}, \quad\ \mbox{ otherwise.} \end{cases} \end{equation*}
\begin{equation*} c(X) = \begin{cases} \text{blue}, \quad \mbox{ if } X\in \bigcup _{{\mathcal{Y}}\in \binom{[N]}{k}}{\mathcal{P}}_{\mathcal{Y}},\\ \text{red}, \quad\ \mbox{ otherwise.} \end{cases} \end{equation*}
Note that for every
![]() ${\mathcal{Y}}\in \binom{[N]}{k}$
,
${\mathcal{Y}}\in \binom{[N]}{k}$
,
![]() ${\mathcal{P}}_{\mathcal{Y}}$
witnesses that there is a blue
${\mathcal{P}}_{\mathcal{Y}}$
witnesses that there is a blue
![]() $\mathcal{Y}$
-shrub in
$\mathcal{Y}$
-shrub in
![]() $Q$
. Recall that a
$Q$
. Recall that a
![]() $\mathcal{Y}$
-shrub is an up-tree. Applying Claim 3 the blue subposet of
$\mathcal{Y}$
-shrub is an up-tree. Applying Claim 3 the blue subposet of
![]() $Q$
is a collection of independent up-trees. Then Lemma 5 provides that the colouring
$Q$
is a collection of independent up-trees. Then Lemma 5 provides that the colouring
![]() $c$
does not contain a blue copy of
$c$
does not contain a blue copy of
![]() $\Lambda$
.
$\Lambda$
.
5. Proof of Theorems 3 and 2
Proof of Theorem 3.
Upper Bound: Let
![]() $k=(1+\epsilon )\frac{n}{\log (n)}$
and consider an arbitrary blue/red coloured Boolean lattice
$k=(1+\epsilon )\frac{n}{\log (n)}$
and consider an arbitrary blue/red coloured Boolean lattice
![]() $Q$
on ground set
$Q$
on ground set
![]() $[n+k]$
with no blue copy of
$[n+k]$
with no blue copy of
![]() $\Lambda$
. Pick any
$\Lambda$
. Pick any
![]() ${\mathcal{Y}}\in \binom{[n+k]}{k}$
and assume that there is a blue
${\mathcal{Y}}\in \binom{[n+k]}{k}$
and assume that there is a blue
![]() $\mathcal{Y}$
-shrub in
$\mathcal{Y}$
-shrub in
![]() $Q$
. Recall that the maximal elements of the
$Q$
. Recall that the maximal elements of the
![]() $\mathcal{Y}$
-shrub form an antichain of size
$\mathcal{Y}$
-shrub form an antichain of size
![]() $k!$
. Sperner’s theorem provides that the largest antichain in
$k!$
. Sperner’s theorem provides that the largest antichain in
![]() $Q$
has size
$Q$
has size
![]() $\binom{n+k}{\lfloor \frac{n+k}{2}\rfloor }$
, so
$\binom{n+k}{\lfloor \frac{n+k}{2}\rfloor }$
, so
![]() $k!\le \binom{n+k}{\lfloor \frac{n+k}{2}\rfloor }\leq 2^{n+k}$
.
$k!\le \binom{n+k}{\lfloor \frac{n+k}{2}\rfloor }\leq 2^{n+k}$
.
We also have that
![]() $k!\gt \left (\tfrac{k}{e}\right )^k=2^{k(\log k - \log e)}.$
By the choice of
$k!\gt \left (\tfrac{k}{e}\right )^k=2^{k(\log k - \log e)}.$
By the choice of
![]() $k$
, we obtain for sufficiently large
$k$
, we obtain for sufficiently large
![]() $n$
,
$n$
,
In particular for sufficiently large
![]() $n$
,
$n$
,
![]() $k\log k -k\log e\gt n+k,$
a contradiction. Thus
$k\log k -k\log e\gt n+k,$
a contradiction. Thus
![]() $Q$
does not contain a blue
$Q$
does not contain a blue
![]() $\mathcal{Y}$
-shrub for this fixed
$\mathcal{Y}$
-shrub for this fixed
![]() $\mathcal{Y}$
. Then Corollary 13 yields that there is a red copy of
$\mathcal{Y}$
. Then Corollary 13 yields that there is a red copy of
![]() $Q_n$
in
$Q_n$
in
![]() $Q$
. Consequently, each blue/red coloured Boolean lattice of dimension
$Q$
. Consequently, each blue/red coloured Boolean lattice of dimension
![]() $n+k$
contains either a blue copy of
$n+k$
contains either a blue copy of
![]() $\Lambda$
or a red copy of
$\Lambda$
or a red copy of
![]() $Q_n$
.
$Q_n$
.
Lower Bound: Let
![]() $N$
sufficiently large, let
$N$
sufficiently large, let
![]() $k=\frac{10}{216}\frac{N}{\ln (N)}$
and
$k=\frac{10}{216}\frac{N}{\ln (N)}$
and
![]() $n=N-k$
. Note that
$n=N-k$
. Note that
![]() $k\le \frac{N}{2}$
, thus
$k\le \frac{N}{2}$
, thus
![]() $n\le N\le 2n$
. Let
$n\le N\le 2n$
. Let
![]() $Q={\mathcal{Q}}([N])$
. By Theorem 18 there exists a colouring of
$Q={\mathcal{Q}}([N])$
. By Theorem 18 there exists a colouring of
![]() $Q$
with no blue copy of
$Q$
with no blue copy of
![]() $\Lambda$
such that for every
$\Lambda$
such that for every
![]() ${\mathcal{Y}}\in \binom{[N]}{k}$
, there is a blue
${\mathcal{Y}}\in \binom{[N]}{k}$
, there is a blue
![]() $\mathcal{Y}$
-shrub. By Corollary 13, there is no red copy of
$\mathcal{Y}$
-shrub. By Corollary 13, there is no red copy of
![]() $Q_n$
in this colouring, thus
$Q_n$
in this colouring, thus
![]() $R(\Lambda,Q_n)\ge N= n+ k$
. It remains to bound
$R(\Lambda,Q_n)\ge N= n+ k$
. It remains to bound
![]() $k$
in terms of
$k$
in terms of
![]() $n$
. Indeed,
$n$
. Indeed,
which concludes the proof.![]()
Proof of Theorem 2. The lower bound on
![]() $R(P, Q_n)$
for
$R(P, Q_n)$
for
![]() $P$
containing either
$P$
containing either
![]() $\Lambda$
or
$\Lambda$
or
![]() $V$
follows from Theorem 3.
$V$
follows from Theorem 3.
Consider now a poset
![]() $P$
that contains neither a copy of
$P$
that contains neither a copy of
![]() $\Lambda$
nor a copy of
$\Lambda$
nor a copy of
![]() $V$
. By Corollary 6,
$V$
. By Corollary 6,
![]() $P$
is a union of independent chains. Assume that
$P$
is a union of independent chains. Assume that
![]() $P$
has
$P$
has
![]() $k$
independent chains on at most
$k$
independent chains on at most
![]() $\ell$
vertices each. Let
$\ell$
vertices each. Let
![]() $K$
be an even integer such that
$K$
be an even integer such that
![]() $\binom{K}{K/2} \geq k$
. Let
$\binom{K}{K/2} \geq k$
. Let
![]() $\mathcal{Y}$
be a set of size
$\mathcal{Y}$
be a set of size
![]() $K$
and let
$K$
and let
![]() $\mathcal{X}$
be a set, disjoint from
$\mathcal{X}$
be a set, disjoint from
![]() $\mathcal{Y}$
of size
$\mathcal{Y}$
of size
![]() $n+ \ell$
. Consider an arbitrary colouring of
$n+ \ell$
. Consider an arbitrary colouring of
![]() ${\mathcal{Q}}({\mathcal{X}}\cup{\mathcal{Y}})$
. Assume that there is no red copy of
${\mathcal{Q}}({\mathcal{X}}\cup{\mathcal{Y}})$
. Assume that there is no red copy of
![]() $Q_n$
. We shall show that there is a blue copy of
$Q_n$
. We shall show that there is a blue copy of
![]() $P$
.
$P$
.
Let
![]() $Y_1, \ldots, Y_k$
form an antichain in
$Y_1, \ldots, Y_k$
form an antichain in
![]() ${\mathcal{Q}}({\mathcal{Y}})$
, its existence is guaranteed by Sperner’s theorem. Let
${\mathcal{Q}}({\mathcal{Y}})$
, its existence is guaranteed by Sperner’s theorem. Let
![]() $Q^i$
be a copy of
$Q^i$
be a copy of
![]() ${\mathcal{Q}}({\mathcal{X}})$
obtained as an image of an embedding
${\mathcal{Q}}({\mathcal{X}})$
obtained as an image of an embedding
![]() $\phi _i\,:\,{\mathcal{Q}}({\mathcal{X}}) \to{\mathcal{Q}}({\mathcal{X}}\cup Y_i)$
,
$\phi _i\,:\,{\mathcal{Q}}({\mathcal{X}}) \to{\mathcal{Q}}({\mathcal{X}}\cup Y_i)$
,
![]() $\phi _i(X)=X\cup Y_i$
for any
$\phi _i(X)=X\cup Y_i$
for any
![]() $X\subseteq{\mathcal{X}}$
. Consider the blue vertices in
$X\subseteq{\mathcal{X}}$
. Consider the blue vertices in
![]() $Q^i$
. If there is no blue chain on
$Q^i$
. If there is no blue chain on
![]() $\ell$
vertices in
$\ell$
vertices in
![]() $Q^i$
, Corollary 9 implies the existence of a red copy of
$Q^i$
, Corollary 9 implies the existence of a red copy of
![]() $Q_n$
in
$Q_n$
in
![]() $Q^i$
, a contradiction. Thus for every
$Q^i$
, a contradiction. Thus for every
![]() $i\in [k]$
, there is a blue copy
$i\in [k]$
, there is a blue copy
![]() $P_i$
of a chain on
$P_i$
of a chain on
![]() $\ell$
vertices in
$\ell$
vertices in
![]() $Q^i$
. Note that for any
$Q^i$
. Note that for any
![]() $A\in Q^i, B\in Q^j$
,
$A\in Q^i, B\in Q^j$
,
![]() $i\neq j$
,
$i\neq j$
,
![]() $A\not \sim B$
, since
$A\not \sim B$
, since
![]() $A\cap{\mathcal{Y}} =Y_i\not \sim Y_j=B\cap{\mathcal{Y}}$
. Thus the
$A\cap{\mathcal{Y}} =Y_i\not \sim Y_j=B\cap{\mathcal{Y}}$
. Thus the
![]() $P_i$
’s are independent chains on
$P_i$
’s are independent chains on
![]() $\ell$
vertices each. Their union contains a copy of
$\ell$
vertices each. Their union contains a copy of
![]() $P$
. This shows that
$P$
. This shows that
![]() $R(P, Q_n) \leq n + K+\ell = n+ f(P)$
.
$R(P, Q_n) \leq n + K+\ell = n+ f(P)$
.![]()
6. Conclusion
In this paper we considered the poset Ramsey number
![]() $R(P,Q_n)$
for a fixed poset
$R(P,Q_n)$
for a fixed poset
![]() $P$
and large
$P$
and large
![]() $n$
. We showed a sharp jump in asymptotic behaviour of this Ramsey number depending on
$n$
. We showed a sharp jump in asymptotic behaviour of this Ramsey number depending on
![]() $P$
. For ‘simple’ posets
$P$
. For ‘simple’ posets
![]() $P$
, those containing neither a copy of
$P$
, those containing neither a copy of
![]() $\Lambda$
nor a copy of
$\Lambda$
nor a copy of
![]() $V$
, the poset Ramsey number of
$V$
, the poset Ramsey number of
![]() $P$
versus
$P$
versus
![]() $Q_n$
deviates from the trivial lower bound
$Q_n$
deviates from the trivial lower bound
![]() $n$
by at most an additive constant. As pointed out in the proof of Theorem 2 these ‘simple’ posets are given by the unions of independent chains. ‘Complicated’ posets, those that contain a copy of
$n$
by at most an additive constant. As pointed out in the proof of Theorem 2 these ‘simple’ posets are given by the unions of independent chains. ‘Complicated’ posets, those that contain a copy of
![]() $\Lambda$
or
$\Lambda$
or
![]() $V$
, behave differently. In this case,
$V$
, behave differently. In this case,
![]() $R(P, Q_n)$
is always notably larger than the trivial lower bound
$R(P, Q_n)$
is always notably larger than the trivial lower bound
![]() $n$
by at least an additive term
$n$
by at least an additive term
![]() $\Omega (n/\log n)$
.
$\Omega (n/\log n)$
.
The best known upper bound for a fixed poset
![]() $P$
and large
$P$
and large
![]() $n$
is given by
$n$
is given by
![]() $R(P, Q_n) \leq C_P\cdot n$
, for a constant
$R(P, Q_n) \leq C_P\cdot n$
, for a constant
![]() $C_P$
, as was shown by Lu and Thompson [Reference Lu and Thompson20]. Here
$C_P$
, as was shown by Lu and Thompson [Reference Lu and Thompson20]. Here
![]() $C_P$
is close to the two-dimension of
$C_P$
is close to the two-dimension of
![]() $P$
, that is the dimension of the smallest Boolean lattice containing a copy of
$P$
, that is the dimension of the smallest Boolean lattice containing a copy of
![]() $P$
. However, we believe that the true value of
$P$
. However, we believe that the true value of
![]() $R(P,Q_n)$
is significantly closer to our lower bound, namely that the difference
$R(P,Q_n)$
is significantly closer to our lower bound, namely that the difference
![]() $R(P,Q_n)-n$
is sublinear in terms of
$R(P,Q_n)-n$
is sublinear in terms of
![]() $n$
.
$n$
.
Conjecture 19.
Let
![]() $n\in{\mathbb{N}}$
and
$n\in{\mathbb{N}}$
and
![]() $P$
be a fixed poset independent from
$P$
be a fixed poset independent from
![]() $n$
. Then
$n$
. Then
Note that this conjecture is equivalent to verifying in the classical off-diagonal setting of poset Ramsey numbers whether for all
![]() $m$
fixed and
$m$
fixed and
![]() $n$
large, it holds that
$n$
large, it holds that
![]() $R(Q_m,Q_n)=n + o(n).$
This is related to a conjecture raised by Lu and Thompson [Reference Lu and Thompson20] claiming that
$R(Q_m,Q_n)=n + o(n).$
This is related to a conjecture raised by Lu and Thompson [Reference Lu and Thompson20] claiming that
![]() $R(Q_m,Q_n)=o(n^2)$
for
$R(Q_m,Q_n)=o(n^2)$
for
![]() $n\ge m$
with
$n\ge m$
with
![]() $n$
and
$n$
and
![]() $m$
sufficiently large.
$m$
sufficiently large.
Acknowledgments
The authors would like to thank Alexander Riasanovsky for comments on the manuscript and the two referees for their careful reading of the paper and their useful comments.
Funding
The research was partially supported by DFG grant FKZ AX 93/2-1.