Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-10T17:40:54.256Z Has data issue: false hasContentIssue false
  • English
  • Français

The Probability of Non-Existence of a Subgraph in a Moderately Sparse Random Graph

Part of: Combinatorial probability Combinatorics Graph theory

Published online by Cambridge University Press:  09 May 2018

DUDLEY STARK  and
NICK WORMALD
DUDLEY STARK
Affiliation:
School of Mathematical Sciences, Queen Mary University of London, London E1 4NS, UK (e-mail: d.s.stark@qmul.ac.uk)
NICK WORMALD
Affiliation:
School of Mathematical Sciences, Monash University, Victoria 3800, Australia (e-mail: nicholas.wormald@monash.edu)
Get access Rights & Permissions [Opens in a new window]

Abstract

We develop a general procedure that finds recursions for statistics counting isomorphic copies of a graph G0 in the common random graph models 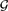${\cal G}$(n,m) and 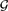${\cal G}$(n,p). Our results apply when the average degrees of the random graphs are below the threshold at which each edge is included in a copy of G0. This extends an argument given earlier by the second author for G0=K3 with a more restricted range of average degree. For all strictly balanced subgraphs G0, our results give much information on the distribution of the number of copies of G0 that are not in large ‘clusters’ of copies. The probability that a random graph in 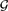${\cal G}$(n,p) has no copies of G0 is shown to be given asymptotically by the exponential of a power series in n and p, over a fairly wide range of p. A corresponding result is also given for 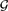${\cal G}$(n,m), which gives an asymptotic formula for the number of graphs with n vertices, m edges and no copies of G0, for the applicable range of m. An example is given, computing the asymptotic probability that a random graph has no triangles for p=o(n−7/11) in 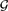${\cal G}$(n,p) and for m=o(n15/11) in 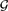${\cal G}$(n,m), extending results of the second author.

MSC classification

Primary: 05C80: Random graphs 05A16: Asymptotic enumeration
Secondary: 60C05: Combinatorial probability
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 27 , Special Issue 4: Special Issue: Oberwolfach Workshop , July 2018 , pp. 672 - 715
Copyright
Copyright © Cambridge University Press 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Bollobás, B. (1981) Random graphs. In Combinatorics: Proceedings (Swansea, 1981), Vol. 52 of London Mathematical Society Lecture Note Series, Cambridge University Press, pp. 80–102.CrossRefGoogle Scholar
[2] Erdős, P., Kleitman, D. J. and Rothschild, B. L. (1976) Asymptotic enumeration of K n-free graphs. In Colloquio Internazionale sulle Teorie Combinatorie (Rome, 1973), Tomo II, Vol. 17 of Atti dei Convegni Lincei, Accad. Naz. Lincei, pp. 19–27.Google Scholar
[3] Frieze, A. (1992) On small subgraphs of random graphs. In Random Graphs (Frieze, A. and Łuczak, T., eds), Vol. 2, Wiley, pp. 67–90.Google Scholar
[4] Janson, S., Łuczak, T. and Ruciński, A. (1990) An exponential bound for the probability of nonexistence of a specified subgraph in a random graph. In Random Graphs '87 (Karoński, M., Jaworski, J. and Ruciński, A., eds), Wiley, pp. 73–87.Google Scholar
[5] Janson, S., Łuczak, T. and Ruciński, A. (2000) Random Graphs, Wiley.Google Scholar
[6] Łuczak, T. (2000) On triangle-free random graphs. Random Struct. Alg. 16 260–276.Google Scholar
[7] Osthus, D., Prömel, H. J. and Taraz, A. (2003) For which densities are random triangle-free graphs almost surely bipartite? Combinatorica 23 105–150.Google Scholar
[8] Prömel, H. J. and Steger, A. (1996) Counting H-free graphs. Discrete Math. 154 311–315.Google Scholar
[9] Prömel, H. J. and Steger, A. (1996) On the asymptotic structure of sparse triangle free graphs. J. Graph Theory 21 137–151.3.0.CO;2-S>CrossRefGoogle Scholar
[10] Ruciński, A. (1988) When are small subgraphs of a random graph normally distributed? Probab. Theory Rel. Fields 78 1–10.CrossRefGoogle Scholar
[11] Wormald, N. C. (1996) The perturbation method and triangle-free random graphs. Random Struct. Alg. 9 253–270.Google Scholar