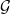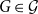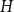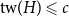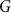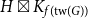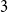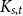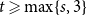1. Introduction
Graph product structure theory describes complicated graphs as subgraphs of strong productsFootnote
1
of simpler building blocks. The building blocks typically have bounded treewidth, which is the standard measure of how similar a graph is to a tree. Examples of graph classes that can be described this way include planar graphs [Reference Dujmović, Joret, Micek, Morin, Ueckerdt and Wood29, Reference Ueckerdt, Wood and Yi73], graphs of bounded Euler genus [Reference Distel, Hickingbotham, Huynh and Wood23, Reference Dujmović, Joret, Micek, Morin, Ueckerdt and Wood29], graphs excluding a fixed minor [Reference Dujmović, Joret, Micek, Morin, Ueckerdt and Wood29], and various non-minor-closed classes [Reference Dujmović, Morin and Wood31, Reference Hickingbotham and Wood41]. These results have been the key to solving several open problems regarding queue layouts [Reference Dujmović, Joret, Micek, Morin, Ueckerdt and Wood29], nonrepetitive colouring [Reference Dujmović, Esperet, Joret, Walczak and Wood28],
![]() $p$
-centered colouring [Reference Döcebski, Felsner, Micek and Schröder25], adjacency labelling [Reference Dujmović, Esperet, Gavoille, Joret, Micek and Morin27, Reference Esperet, Joret and Morin36], twin-width [Reference Bekos, Da Lozzo, Hliněný and Kaufmann3, Reference Édouard Bonnet and Wood11], and comparable box dimension [Reference Dvorák, Gonçalves, Lahiri, Tan and Ueckerdt33].
$p$
-centered colouring [Reference Döcebski, Felsner, Micek and Schröder25], adjacency labelling [Reference Dujmović, Esperet, Gavoille, Joret, Micek and Morin27, Reference Esperet, Joret and Morin36], twin-width [Reference Bekos, Da Lozzo, Hliněný and Kaufmann3, Reference Édouard Bonnet and Wood11], and comparable box dimension [Reference Dvorák, Gonçalves, Lahiri, Tan and Ueckerdt33].
This paper shows that graph product structure theory can even be used to describe graphs of bounded treewidth in terms of simpler graphs. Here the building blocks are graphs of smaller treewidth and complete graphs of bounded size. For example, a classical theorem by the referee of [Reference Ding and Oporowski19] can be interpreted as saying that every graph
![]() $G$
of treewidth
$G$
of treewidth
![]() $k$
and maximum degree
$k$
and maximum degree
![]() $\Delta$
is containedFootnote
2
in
$\Delta$
is containedFootnote
2
in
![]() $T \boxtimes K_{O(k\Delta )}$
for some tree
$T \boxtimes K_{O(k\Delta )}$
for some tree
![]() $T$
.
$T$
.
This result motivates the following definition. The underlying treewidth of a graph class
![]() $\mathcal{G}$
is the minimum
$\mathcal{G}$
is the minimum
![]() $c \in{\mathbb{N}}_0$
such that, for some function
$c \in{\mathbb{N}}_0$
such that, for some function
![]() $f$
, for every graph
$f$
, for every graph
![]() $G \in \mathcal{G}$
there is a graph
$G \in \mathcal{G}$
there is a graph
![]() $H$
with
$H$
with
![]() $\textrm{tw}(H) \leqslant c$
such that
$\textrm{tw}(H) \leqslant c$
such that
![]() $G$
is contained in
$G$
is contained in
![]() $H \boxtimes K_{f(\textrm{tw}(G))}$
. If there is no such
$H \boxtimes K_{f(\textrm{tw}(G))}$
. If there is no such
![]() $c$
, then
$c$
, then
![]() $\mathcal{G}$
has unbounded underlying treewidth. We call
$\mathcal{G}$
has unbounded underlying treewidth. We call
![]() $f$
the treewidth-binding function. For example, the above-mentioned result in [Reference Ding and Oporowski19] says that any graph class with bounded degree has underlying treewidth at most
$f$
the treewidth-binding function. For example, the above-mentioned result in [Reference Ding and Oporowski19] says that any graph class with bounded degree has underlying treewidth at most
![]() $1$
with treewidth-binding function
$1$
with treewidth-binding function
![]() $O(k)$
.
$O(k)$
.
This paper introduces disjointed coverings of graphs and shows that they are intimately related to underlying treewidth; see Section 3. Indeed, we show that disjointed coverings characterise the underlying treewidth of any graph class (Theorem 11). The remainder of the paper uses disjointed coverings to determine the underlying treewidth of several graph classes of interest, with a small treewidth-binding function as a secondary goal.
Minor-closed classes: We prove that every planar graph of treewidth
![]() $k$
is contained in
$k$
is contained in
![]() $H \boxtimes K_{O(k^2)}$
where
$H \boxtimes K_{O(k^2)}$
where
![]() $H$
is a graph of treewidth
$H$
is a graph of treewidth
![]() $3$
. Moreover, this bound on the treewidth of
$3$
. Moreover, this bound on the treewidth of
![]() $H$
is best possible. Thus the class of planar graphs has underlying treewidth
$H$
is best possible. Thus the class of planar graphs has underlying treewidth
![]() $3$
(Theorem 21). We prove the following generalisations of this result: the class of graphs embeddable on any fixed surface has underlying treewidth
$3$
(Theorem 21). We prove the following generalisations of this result: the class of graphs embeddable on any fixed surface has underlying treewidth
![]() $3$
(Theorem 22); the class of
$3$
(Theorem 22); the class of
![]() $K_{t}$
-minor-free graphs has underlying treewidth
$K_{t}$
-minor-free graphs has underlying treewidth
![]() $t-2$
(Theorem 18); and for
$t-2$
(Theorem 18); and for
![]() $t \geqslant \max \{s,3\}$
the class of
$t \geqslant \max \{s,3\}$
the class of
![]() $K_{s,t}$
-minor-free graphs has underlying treewidth
$K_{s,t}$
-minor-free graphs has underlying treewidth
![]() $s$
(Theorem 19). In all these results, the treewidth-binding function is
$s$
(Theorem 19). In all these results, the treewidth-binding function is
![]() $O(k^2)$
for fixed
$O(k^2)$
for fixed
![]() $s$
and
$s$
and
![]() $t$
.
$t$
.
Monotone classes: We characterise the monotone graph classes with bounded underlying treewidth. We show that a monotone graph class
![]() $\mathcal{G}$
has bounded underlying treewidth if and only if
$\mathcal{G}$
has bounded underlying treewidth if and only if
![]() $\mathcal{G}$
excludes some fixed topological minor (Theorem 28). In particular, we show that for
$\mathcal{G}$
excludes some fixed topological minor (Theorem 28). In particular, we show that for
![]() $t \geqslant 5$
the class of
$t \geqslant 5$
the class of
![]() $K_t$
-topological-minor-free graphs has underlying treewidth
$K_t$
-topological-minor-free graphs has underlying treewidth
![]() $t$
(Theorem 25). The characterisation for monotone classes has immediate consequences. For example, it implies that the class of
$t$
(Theorem 25). The characterisation for monotone classes has immediate consequences. For example, it implies that the class of
![]() $1$
-planar graphs has unbounded underlying treewidth. On the other hand, for any
$1$
-planar graphs has unbounded underlying treewidth. On the other hand, for any
![]() $k \in{\mathbb{N}}$
, we show that the class of outer
$k \in{\mathbb{N}}$
, we show that the class of outer
![]() $k$
-planar graphs has underlying treewidth
$k$
-planar graphs has underlying treewidth
![]() $2$
(Theorem 46), which generalises the well-known fact that outerplanar graphs have treewidth
$2$
(Theorem 46), which generalises the well-known fact that outerplanar graphs have treewidth
![]() $2$
.
$2$
.
We use our result for disjointed coverings to characterise the graphs
![]() $H$
for which the class of
$H$
for which the class of
![]() $H$
-free graphs has bounded underlying treewidth. In particular, the class of
$H$
-free graphs has bounded underlying treewidth. In particular, the class of
![]() $H$
-free graphs has bounded underlying treewidth if and only if every component of
$H$
-free graphs has bounded underlying treewidth if and only if every component of
![]() $H$
is a subdivided star (Theorem 29). For specific graphs
$H$
is a subdivided star (Theorem 29). For specific graphs
![]() $H$
, including paths and disjoint unions of paths, we precisely determine the underlying treewidth of the class of
$H$
, including paths and disjoint unions of paths, we precisely determine the underlying treewidth of the class of
![]() $H$
-free graphs.
$H$
-free graphs.
Hereditary classes: We characterise the graphs
![]() $H$
for which the class of graphs with no induced subgraph isomorphic to
$H$
for which the class of graphs with no induced subgraph isomorphic to
![]() $H$
has bounded underlying treewidth. The answer is precisely when every component of
$H$
has bounded underlying treewidth. The answer is precisely when every component of
![]() $H$
is a star, in which case the underlying treewidth is at most
$H$
is a star, in which case the underlying treewidth is at most
![]() $2$
. Moreover, we characterise the graphs
$2$
. Moreover, we characterise the graphs
![]() $H$
for which the class of graphs with no induced subgraph isomorphic to
$H$
for which the class of graphs with no induced subgraph isomorphic to
![]() $H$
has underlying treewidth
$H$
has underlying treewidth
![]() $0$
,
$0$
,
![]() $1$
or
$1$
or
![]() $2$
(Theorem 38).
$2$
(Theorem 38).
Universal graphs: A graph
![]() $U$
is universal for a graph class
$U$
is universal for a graph class
![]() $\mathcal{G}$
if
$\mathcal{G}$
if
![]() $U \in \mathcal{G}$
and
$U \in \mathcal{G}$
and
![]() $U$
contains every graph in
$U$
contains every graph in
![]() $\mathcal{G}$
. This definition is only interesting when considering infinite graphs. For each
$\mathcal{G}$
. This definition is only interesting when considering infinite graphs. For each
![]() $k \in{\mathbb{N}}$
there is a universal graph
$k \in{\mathbb{N}}$
there is a universal graph
![]() $\mathcal{T}_k$
for the class of countable graphs of treewidth
$\mathcal{T}_k$
for the class of countable graphs of treewidth
![]() $k$
. Huynh, Mohar, Šámal, Thomassen, and Wood [Reference Huynh, Mohar, Šámal, Thomassen and Wood42] gave an explicit construction for
$k$
. Huynh, Mohar, Šámal, Thomassen, and Wood [Reference Huynh, Mohar, Šámal, Thomassen and Wood42] gave an explicit construction for
![]() $\mathcal{T}_k$
, and showed how product structure theorems for finite graphs lead to universal graphs. Their results imply that for any hereditary class
$\mathcal{T}_k$
, and showed how product structure theorems for finite graphs lead to universal graphs. Their results imply that for any hereditary class
![]() $\mathcal{G}$
of countable graphs, if the class of finite graphs in
$\mathcal{G}$
of countable graphs, if the class of finite graphs in
![]() $\mathcal{G}$
has underlying treewidth
$\mathcal{G}$
has underlying treewidth
![]() $c$
with treewidth-binding function
$c$
with treewidth-binding function
![]() $f$
, then every graph in
$f$
, then every graph in
![]() $\mathcal{G}$
of treewidth at most
$\mathcal{G}$
of treewidth at most
![]() $k$
is contained in
$k$
is contained in
![]() $\mathcal{T}_c \boxtimes K_{f(k)}$
. This result is applicable to all the classes above. For example, every countable
$\mathcal{T}_c \boxtimes K_{f(k)}$
. This result is applicable to all the classes above. For example, every countable
![]() $K_t$
-minor-free graph of treewidth
$K_t$
-minor-free graph of treewidth
![]() $k$
is contained in
$k$
is contained in
![]() $\mathcal{T}_{t-2} \boxtimes K_{O(k^2)}$
.
$\mathcal{T}_{t-2} \boxtimes K_{O(k^2)}$
.
The definition of underlying treewidth suggests an underlying version of any graph parameter. An extended version of this paper [Reference Campbell12] explores this idea, focusing on underlying chromatic number. It also includes details of some straightforward proofs omitted from this version.
The rest of this paper is organised as follows. Section 2 introduces some standard structural graph theory notions that will be useful. Section 3 presents disjointed coverings, our main technical tool that characterises underlying treewidth. Section 4 defines two graphs that provide lower bounds on the underlying treewidth of many graph classes. Sections 5–8 address the underlying treewidth of graph classes defined by excluded minors, topological minors, subgraphs, and induced subgraphs, respectively. Finally, Section 9 considers graphs defined by their drawings.
2. Preliminaries
2.1. Basic definitions
See [Reference Diestel17] for graph-theoretic definitions not given here. We consider simple, finite, undirected graphs
![]() $G$
with vertex-set
$G$
with vertex-set
![]() $V(G)$
and edge-set
$V(G)$
and edge-set
![]() $E(G)$
. A graph class is a collection of graphs closed under isomorphism. A graph class is hereditary if it is closed under taking induced subgraphs. A graph class is monotone if it is closed under taking subgraphs. A graph
$E(G)$
. A graph class is a collection of graphs closed under isomorphism. A graph class is hereditary if it is closed under taking induced subgraphs. A graph class is monotone if it is closed under taking subgraphs. A graph
![]() $H$
is a minor of a graph
$H$
is a minor of a graph
![]() $G$
if
$G$
if
![]() $H$
is isomorphic to a graph obtained from a subgraph of
$H$
is isomorphic to a graph obtained from a subgraph of
![]() $G$
by contracting edges. A graph
$G$
by contracting edges. A graph
![]() $G$
is
$G$
is
![]() $H$
-minor-free if
$H$
-minor-free if
![]() $H$
is not a minor of
$H$
is not a minor of
![]() $G$
. A graph class
$G$
. A graph class
![]() $\mathcal{G}$
is minor-closed if every minor of each graph in
$\mathcal{G}$
is minor-closed if every minor of each graph in
![]() $\mathcal{G}$
is also in
$\mathcal{G}$
is also in
![]() $\mathcal{G}$
.
$\mathcal{G}$
.
The class of planar graphs is minor-closed. More generally, the class of graphs embeddable on a given surface (that is, a closed compact
![]() $2$
-manifold) is minor-closed. The Euler genus of a surface with
$2$
-manifold) is minor-closed. The Euler genus of a surface with
![]() $h$
handles and
$h$
handles and
![]() $c$
cross-caps is
$c$
cross-caps is
![]() $2h+c$
. The Euler genus of a graph
$2h+c$
. The Euler genus of a graph
![]() $G$
is the minimum
$G$
is the minimum
![]() $g \in{\mathbb{N}}_0$
such that there is an embedding of
$g \in{\mathbb{N}}_0$
such that there is an embedding of
![]() $G$
in a surface of Euler genus
$G$
in a surface of Euler genus
![]() $g$
; see [Reference Mohar and Thomassen56] for more about graph embeddings in surfaces. A graph is linklessly embeddable if it has an embedding in
$g$
; see [Reference Mohar and Thomassen56] for more about graph embeddings in surfaces. A graph is linklessly embeddable if it has an embedding in
![]() $\mathbb{R}^3$
with no two linked cycles; see [Reference Robertson, Seymour and Thomas66] for a survey and precise definitions. The class of linklessly embeddable graphs is also minor-closed.
$\mathbb{R}^3$
with no two linked cycles; see [Reference Robertson, Seymour and Thomas66] for a survey and precise definitions. The class of linklessly embeddable graphs is also minor-closed.
A graph
![]() $\tilde{G}$
is a subdivision of a graph
$\tilde{G}$
is a subdivision of a graph
![]() $G$
if
$G$
if
![]() $\tilde{G}$
can be obtained from
$\tilde{G}$
can be obtained from
![]() $G$
by replacing each edge
$G$
by replacing each edge
![]() $vw$
by a path
$vw$
by a path
![]() $P_{vw}$
with endpoints
$P_{vw}$
with endpoints
![]() $v$
and
$v$
and
![]() $w$
(internally disjoint from the rest of
$w$
(internally disjoint from the rest of
![]() $\tilde{G}$
). If each
$\tilde{G}$
). If each
![]() $P_{vw}$
has
$P_{vw}$
has
![]() $t$
internal vertices, then
$t$
internal vertices, then
![]() $\tilde{G}$
is the
$\tilde{G}$
is the
![]() $t$
-subdivision of
$t$
-subdivision of
![]() $G$
. If each
$G$
. If each
![]() $P_{vw}$
has at most
$P_{vw}$
has at most
![]() $t$
internal vertices, then
$t$
internal vertices, then
![]() $\tilde{G}$
is a
$\tilde{G}$
is a
![]() $(\leqslant t)$
-subdivision of
$(\leqslant t)$
-subdivision of
![]() $G$
. A graph
$G$
. A graph
![]() $H$
is a topological minor of
$H$
is a topological minor of
![]() $G$
if a subgraph of
$G$
if a subgraph of
![]() $G$
is isomorphic to a subdivision of
$G$
is isomorphic to a subdivision of
![]() $H$
. A graph
$H$
. A graph
![]() $G$
is
$G$
is
![]() $H$
-topological-minor-free if
$H$
-topological-minor-free if
![]() $H$
is not a topological minor of
$H$
is not a topological minor of
![]() $G$
.
$G$
.
A clique in a graph is a set of pairwise adjacent vertices. Let
![]() $\omega (G)$
be the size of the largest clique in a graph
$\omega (G)$
be the size of the largest clique in a graph
![]() $G$
. An independent set in a graph is a set of pairwise non-adjacent vertices. Let
$G$
. An independent set in a graph is a set of pairwise non-adjacent vertices. Let
![]() $\alpha (G)$
be the size of the largest independent set in a graph
$\alpha (G)$
be the size of the largest independent set in a graph
![]() $G$
. Let
$G$
. Let
![]() $\chi (G)$
be the chromatic number of
$\chi (G)$
be the chromatic number of
![]() $G$
. Note that
$G$
. Note that
![]() $|V(G)| \leqslant \chi (G)\alpha (G)$
. A graph
$|V(G)| \leqslant \chi (G)\alpha (G)$
. A graph
![]() $G$
is
$G$
is
![]() $d$
-degenerate if every non-empty subgraph of
$d$
-degenerate if every non-empty subgraph of
![]() $G$
has a vertex of degree at most
$G$
has a vertex of degree at most
![]() $d$
. A greedy algorithm shows that
$d$
. A greedy algorithm shows that
![]() $\chi (G) \leqslant d+1$
for every
$\chi (G) \leqslant d+1$
for every
![]() $d$
-degenerate graph
$d$
-degenerate graph
![]() $G$
.
$G$
.
Let
![]() $P_n$
be the
$P_n$
be the
![]() $n$
-vertex path. For a graph
$n$
-vertex path. For a graph
![]() $G$
and
$G$
and
![]() $\ell \in{\mathbb{N}}$
, let
$\ell \in{\mathbb{N}}$
, let
![]() $\ell \,G$
be the union of
$\ell \,G$
be the union of
![]() $\ell$
vertex-disjoint copies of
$\ell$
vertex-disjoint copies of
![]() $G$
. Let
$G$
. Let
![]() $\widehat{G}$
be the graph obtained from
$\widehat{G}$
be the graph obtained from
![]() $G$
by adding one dominant vertex.
$G$
by adding one dominant vertex.
Let
![]() ${\mathbb{N}} \,:\!=\, \{1,2,\dots \}$
and
${\mathbb{N}} \,:\!=\, \{1,2,\dots \}$
and
![]() ${\mathbb{N}}_0 \,:\!=\, \{0,1,\dots \}$
. All logarithms in this paper are binary.
${\mathbb{N}}_0 \,:\!=\, \{0,1,\dots \}$
. All logarithms in this paper are binary.
2.2. Tree-decompositions
For a tree
![]() $T$
, a
$T$
, a
![]() $T$
-decomposition of a graph
$T$
-decomposition of a graph
![]() $G$
is a collection
$G$
is a collection
![]() $\mathcal{W} = (W_x \,:\, x \in V(T))$
of subsets of
$\mathcal{W} = (W_x \,:\, x \in V(T))$
of subsets of
![]() $V(G)$
indexed by the nodes of
$V(G)$
indexed by the nodes of
![]() $T$
such that (i) for every edge
$T$
such that (i) for every edge
![]() $vw \in E(G)$
, there exists a node
$vw \in E(G)$
, there exists a node
![]() $x \in V(T)$
with
$x \in V(T)$
with
![]() $v,w \in W_x$
; and (ii) for every vertex
$v,w \in W_x$
; and (ii) for every vertex
![]() $v \in V(G)$
, the set
$v \in V(G)$
, the set
![]() $\{ x \in V(T) \,:\, v \in W_x \}$
induces a (connected) subtree of
$\{ x \in V(T) \,:\, v \in W_x \}$
induces a (connected) subtree of
![]() $T$
. Each set
$T$
. Each set
![]() $W_x$
in
$W_x$
in
![]() $\mathcal{W}$
is called a bag. The width of
$\mathcal{W}$
is called a bag. The width of
![]() $\mathcal{W}$
is
$\mathcal{W}$
is
![]() $\max \{ |W_x| \,:\, x \in V(T) \}-1$
. A tree-decomposition is a
$\max \{ |W_x| \,:\, x \in V(T) \}-1$
. A tree-decomposition is a
![]() $T$
-decomposition for any tree
$T$
-decomposition for any tree
![]() $T$
. The treewidth
$T$
. The treewidth
![]() $\textrm{tw}(G)$
of a graph
$\textrm{tw}(G)$
of a graph
![]() $G$
is the minimum width of a tree-decomposition of
$G$
is the minimum width of a tree-decomposition of
![]() $G$
. Treewidth is the standard measure of how similar a graph is to a tree. Indeed, a connected graph has treewidth
$G$
. Treewidth is the standard measure of how similar a graph is to a tree. Indeed, a connected graph has treewidth
![]() $1$
if and only if it is a tree. Treewidth is of fundamental importance in structural and algorithmic graph theory; see [Reference Bodlaender6, Reference Harvey and Wood40, Reference Reed62] for surveys.
$1$
if and only if it is a tree. Treewidth is of fundamental importance in structural and algorithmic graph theory; see [Reference Bodlaender6, Reference Harvey and Wood40, Reference Reed62] for surveys.
We use the following well-known facts about treewidth. Every (topological) minor
![]() $H$
of a graph
$H$
of a graph
![]() $G$
satisfies
$G$
satisfies
![]() $\textrm{tw}(H) \leqslant \textrm{tw}(G)$
. In every tree-decomposition of a graph
$\textrm{tw}(H) \leqslant \textrm{tw}(G)$
. In every tree-decomposition of a graph
![]() $G$
, each clique of
$G$
, each clique of
![]() $G$
appears in some bag. Thus
$G$
appears in some bag. Thus
![]() $\textrm{tw}(G) \geqslant \omega (G)-1$
and
$\textrm{tw}(G) \geqslant \omega (G)-1$
and
![]() $\textrm{tw}(K_n) = n-1$
. If
$\textrm{tw}(K_n) = n-1$
. If
![]() $\{v_1,\dots,v_k\}$
is a clique in a graph
$\{v_1,\dots,v_k\}$
is a clique in a graph
![]() $G_1$
and
$G_1$
and
![]() $\{w_1,\dots,w_k\}$
is a clique in a graph
$\{w_1,\dots,w_k\}$
is a clique in a graph
![]() $G_2$
, and
$G_2$
, and
![]() $G$
is the graph obtained from the disjoint union of
$G$
is the graph obtained from the disjoint union of
![]() $G_1$
and
$G_1$
and
![]() $G_2$
by identifying
$G_2$
by identifying
![]() $v_i$
and
$v_i$
and
![]() $w_i$
for each
$w_i$
for each
![]() $i \in \{1,\dots,k\}$
, then
$i \in \{1,\dots,k\}$
, then
![]() $\textrm{tw}(G) = \max \{\textrm{tw}(G_1),\textrm{tw}(G_2)\}$
. For any graph
$\textrm{tw}(G) = \max \{\textrm{tw}(G_1),\textrm{tw}(G_2)\}$
. For any graph
![]() $G$
, we have
$G$
, we have
![]() $\textrm{tw}(\widehat{G}) = \textrm{tw}(G) + 1$
and
$\textrm{tw}(\widehat{G}) = \textrm{tw}(G) + 1$
and
![]() $\textrm{tw}(\ell \, G) = \textrm{tw}(G)$
for any
$\textrm{tw}(\ell \, G) = \textrm{tw}(G)$
for any
![]() $\ell \in{\mathbb{N}}$
, implying
$\ell \in{\mathbb{N}}$
, implying
![]() $\textrm{tw}(\widehat{\ell \, G}) = \textrm{tw}(G)+1$
. Finally, every graph
$\textrm{tw}(\widehat{\ell \, G}) = \textrm{tw}(G)+1$
. Finally, every graph
![]() $G$
is
$G$
is
![]() $\textrm{tw}(G)$
-degenerate, implying
$\textrm{tw}(G)$
-degenerate, implying
![]() $\chi (G) \leqslant \textrm{tw}(G)+1$
.
$\chi (G) \leqslant \textrm{tw}(G)+1$
.
2.3. Partitions
To describe our main results in Section 1, it is convenient to use the language of graph products. However, to prove our results, it is convenient to work with the equivalent notion of graph partitions, which we now introduce.
For graphs
![]() $G$
and
$G$
and
![]() $H$
, an
$H$
, an
![]() $H$
-partition of
$H$
-partition of
![]() $G$
is a partition
$G$
is a partition
![]() $(V_x \,:\, x\in V(H))$
of
$(V_x \,:\, x\in V(H))$
of
![]() $V(G)$
indexed by the nodes of
$V(G)$
indexed by the nodes of
![]() $H$
, such that for every edge
$H$
, such that for every edge
![]() $vw$
of
$vw$
of
![]() $G$
, if
$G$
, if
![]() $v \in V_x$
and
$v \in V_x$
and
![]() $w \in V_y$
, then
$w \in V_y$
, then
![]() $x = y$
or
$x = y$
or
![]() $xy \in E(H)$
. We say that
$xy \in E(H)$
. We say that
![]() $H$
is the quotient of such a partition. The width of such an
$H$
is the quotient of such a partition. The width of such an
![]() $H$
-partition is
$H$
-partition is
![]() $\max \{ |V_x| \,:\, x \in V(H)\}$
. For
$\max \{ |V_x| \,:\, x \in V(H)\}$
. For
![]() $c \in{\mathbb{N}}_0$
, an
$c \in{\mathbb{N}}_0$
, an
![]() $H$
-partition where
$H$
-partition where
![]() $\textrm{tw}(H) \leqslant c$
is called a
$\textrm{tw}(H) \leqslant c$
is called a
![]() $c$
-tree-partition. The
$c$
-tree-partition. The
![]() $c$
-tree-partition-width of a graph
$c$
-tree-partition-width of a graph
![]() $G$
, denoted
$G$
, denoted
![]() $\textrm{tpw}_c(G)$
, is the minimum width of a
$\textrm{tpw}_c(G)$
, is the minimum width of a
![]() $c$
-tree-partition of
$c$
-tree-partition of
![]() $G$
.
$G$
.
It follows from the definitions that a graph
![]() $G$
has an
$G$
has an
![]() $H$
-partition of width at most
$H$
-partition of width at most
![]() $\ell$
if and only if
$\ell$
if and only if
![]() $G$
is contained in
$G$
is contained in
![]() $H \boxtimes K_\ell$
. Thus,
$H \boxtimes K_\ell$
. Thus,
![]() $\textrm{tpw}_c(G)$
equals the minimum
$\textrm{tpw}_c(G)$
equals the minimum
![]() $\ell \in{\mathbb{N}}_0$
such that
$\ell \in{\mathbb{N}}_0$
such that
![]() $G$
is contained in
$G$
is contained in
![]() $H \boxtimes K_{\ell }$
for some graph
$H \boxtimes K_{\ell }$
for some graph
![]() $H$
with
$H$
with
![]() $\textrm{tw}(H) \leqslant c$
. Hence, the underlying treewidth of a graph class
$\textrm{tw}(H) \leqslant c$
. Hence, the underlying treewidth of a graph class
![]() $\mathcal{G}$
equals the minimum
$\mathcal{G}$
equals the minimum
![]() $c \in{\mathbb{N}}_0$
such that, for some function
$c \in{\mathbb{N}}_0$
such that, for some function
![]() $f$
, every graph
$f$
, every graph
![]() $G \in \mathcal{G}$
has
$G \in \mathcal{G}$
has
![]() $c$
-tree-partition-width at most
$c$
-tree-partition-width at most
![]() $f(\textrm{tw}(G))$
. We henceforth use this as our working definition of underlying treewidth.
$f(\textrm{tw}(G))$
. We henceforth use this as our working definition of underlying treewidth.
If a graph
![]() $G$
has an
$G$
has an
![]() $H$
-partition for some graph
$H$
-partition for some graph
![]() $H$
of treewidth
$H$
of treewidth
![]() $c$
, then we may assume that
$c$
, then we may assume that
![]() $H$
is edge-maximal of treewidth
$H$
is edge-maximal of treewidth
![]() $c$
. So
$c$
. So
![]() $H$
is a
$H$
is a
![]() $c$
-tree (which justifies the ‘
$c$
-tree (which justifies the ‘
![]() $c$
-tree-partition’ terminology). Such graphs
$c$
-tree-partition’ terminology). Such graphs
![]() $H$
are chordal. Chordal partitions are well studied with several applications [Reference Huynh, Mohar, Šámal, Thomassen and Wood42, Reference Reed and Seymour63, Reference Scott, Seymour and Wood68, Reference van den Heuvel, de Mendez, Quiroz, Rabinovich and Siebertz74, Reference van den Heuvel and Wood75]. For example, van den Heuvel and Wood [Reference van den Heuvel and Wood75] proved that every
$H$
are chordal. Chordal partitions are well studied with several applications [Reference Huynh, Mohar, Šámal, Thomassen and Wood42, Reference Reed and Seymour63, Reference Scott, Seymour and Wood68, Reference van den Heuvel, de Mendez, Quiroz, Rabinovich and Siebertz74, Reference van den Heuvel and Wood75]. For example, van den Heuvel and Wood [Reference van den Heuvel and Wood75] proved that every
![]() $K_t$
-minor-free graph has a
$K_t$
-minor-free graph has a
![]() $(t-2)$
-tree-partition in which each part induces a connected subgraph with maximum degree at most
$(t-2)$
-tree-partition in which each part induces a connected subgraph with maximum degree at most
![]() $t-2$
(amongst other properties). Our results give chordal partitions with bounded-size parts (for graphs of bounded treewidth).
$t-2$
(amongst other properties). Our results give chordal partitions with bounded-size parts (for graphs of bounded treewidth).
Before continuing, we review work on the
![]() $c = 1$
case. A tree-partition is a
$c = 1$
case. A tree-partition is a
![]() $T$
-partition for some tree
$T$
-partition for some tree
![]() $T$
. The tree-partition-width
Footnote
3
of
$T$
. The tree-partition-width
Footnote
3
of
![]() $G$
, denoted by
$G$
, denoted by
![]() $\textrm{tpw}(G)$
, is the minimum width of a tree-partition of
$\textrm{tpw}(G)$
, is the minimum width of a tree-partition of
![]() $G$
. Thus
$G$
. Thus
![]() $\textrm{tpw}(G) = \textrm{tpw}_1(G)$
, which equals the minimum
$\textrm{tpw}(G) = \textrm{tpw}_1(G)$
, which equals the minimum
![]() $\ell \in{\mathbb{N}}_0$
for which
$\ell \in{\mathbb{N}}_0$
for which
![]() $G$
is contained in
$G$
is contained in
![]() $T \boxtimes K_\ell$
for some tree
$T \boxtimes K_\ell$
for some tree
![]() $T$
. Tree-partitions were independently introduced by Seese [Reference Seese69] and Halin [Reference Halin39], and have since been widely investigated [Reference Bodlaender7, Reference Bodlaender and Engelfriet8, Reference Ding and Oporowski19, Reference Ding and Oporowski20, Reference Distel and Wood24, Reference Edenbrandt34, Reference Wood76, Reference Wood77]. Applications of tree-partitions include graph drawing [Reference Carmi, Dujmović, Morin and Wood13, Reference Di Giacomo, Liotta and Meijer16, Reference Dujmović, Morin and Wood30, Reference Dujmović, Suderman and Wood32, Reference Wood and Telle80], nonrepetitive graph colouring [Reference Barát and Wood2], clustered graph colouring [Reference Alon, Ding, Oporowski and Vertigan1], monadic second-order logic [Reference Kuske and Lohrey51], network emulations [Reference Bodlaender4, Reference Bodlaender5, Reference Bodlaender and van Leeuwen9, Reference Fishburn and Finkel37], size Ramsey number [Reference Draganić, Kaufmann, Correia, Petrova and Steiner26, Reference Kamcev, Liebenau, Wood and Yepremyan43], statistical learning theory [Reference Zhang and Amini81], and the edge-Erdős-Pósa property [Reference Chatzidimitriou, Raymond, Sau and Thilikos14, Reference Giannopoulou, Kwon, Raymond and Thilikos38, Reference Raymond and Thilikos60]. Planar-partitions and other more general structures have also been studied [Reference Diestel and Kühn18, Reference Ding, Oporowski, Sanders and Vertigan21, Reference Ding, Oporowski, Sanders and Vertigan22, Reference Reed and Seymour63, Reference Wood and Telle80].
$T$
. Tree-partitions were independently introduced by Seese [Reference Seese69] and Halin [Reference Halin39], and have since been widely investigated [Reference Bodlaender7, Reference Bodlaender and Engelfriet8, Reference Ding and Oporowski19, Reference Ding and Oporowski20, Reference Distel and Wood24, Reference Edenbrandt34, Reference Wood76, Reference Wood77]. Applications of tree-partitions include graph drawing [Reference Carmi, Dujmović, Morin and Wood13, Reference Di Giacomo, Liotta and Meijer16, Reference Dujmović, Morin and Wood30, Reference Dujmović, Suderman and Wood32, Reference Wood and Telle80], nonrepetitive graph colouring [Reference Barát and Wood2], clustered graph colouring [Reference Alon, Ding, Oporowski and Vertigan1], monadic second-order logic [Reference Kuske and Lohrey51], network emulations [Reference Bodlaender4, Reference Bodlaender5, Reference Bodlaender and van Leeuwen9, Reference Fishburn and Finkel37], size Ramsey number [Reference Draganić, Kaufmann, Correia, Petrova and Steiner26, Reference Kamcev, Liebenau, Wood and Yepremyan43], statistical learning theory [Reference Zhang and Amini81], and the edge-Erdős-Pósa property [Reference Chatzidimitriou, Raymond, Sau and Thilikos14, Reference Giannopoulou, Kwon, Raymond and Thilikos38, Reference Raymond and Thilikos60]. Planar-partitions and other more general structures have also been studied [Reference Diestel and Kühn18, Reference Ding, Oporowski, Sanders and Vertigan21, Reference Ding, Oporowski, Sanders and Vertigan22, Reference Reed and Seymour63, Reference Wood and Telle80].
Bounded tree-partition-width implies bounded treewidth, as noted by Seese [Reference Seese69]. This fact easily generalises for
![]() $c$
-tree-partition-width; see [Reference Campbell12] for a proof.
$c$
-tree-partition-width; see [Reference Campbell12] for a proof.
Observation 1.
For every graph
![]() $G$
and
$G$
and
![]() $c\in{\mathbb{N}}_0$
, we have
$c\in{\mathbb{N}}_0$
, we have
![]() $\textrm{tw}(G) \leqslant (c+1)\textrm{tpw}_c(G)-1$
.
$\textrm{tw}(G) \leqslant (c+1)\textrm{tpw}_c(G)-1$
.
Of course,
![]() $\textrm{tw}(T) = \textrm{tpw}(T) = 1$
for every tree
$\textrm{tw}(T) = \textrm{tpw}(T) = 1$
for every tree
![]() $T$
. But in general,
$T$
. But in general,
![]() $\textrm{tpw}(G)$
can be much larger than
$\textrm{tpw}(G)$
can be much larger than
![]() $\textrm{tw}(G)$
. For example, fan graphs on
$\textrm{tw}(G)$
. For example, fan graphs on
![]() $n$
vertices have treewidth
$n$
vertices have treewidth
![]() $2$
and tree-partition-width
$2$
and tree-partition-width
![]() $\Omega (\sqrt{n})$
; see Lemma 12 below. On the other hand, the referee of [Reference Ding and Oporowski19] showed that if the maximum degree and treewidth are both bounded, then so is the tree-partition-width, which is one of the most useful results about tree-partitions.
$\Omega (\sqrt{n})$
; see Lemma 12 below. On the other hand, the referee of [Reference Ding and Oporowski19] showed that if the maximum degree and treewidth are both bounded, then so is the tree-partition-width, which is one of the most useful results about tree-partitions.
Lemma 2 ([Reference Ding and Oporowski19]). For
![]() $k,\Delta \in{\mathbb{N}}$
, every graph of treewidth less than
$k,\Delta \in{\mathbb{N}}$
, every graph of treewidth less than
![]() $k$
and maximum degree at most
$k$
and maximum degree at most
![]() $\Delta$
has tree-partition-width at most
$\Delta$
has tree-partition-width at most
![]() $24k\Delta$
.
$24k\Delta$
.
This bound is best possible up to the multiplicative constant [Reference Wood77]. Note that bounded maximum degree is not necessary for bounded tree-partition-width (for example, stars). Ding and Oporowski [Reference Ding and Oporowski20] characterised graph classes with bounded tree-partition-width in terms of excluded topological minors. We give an alternative characterisation, which says that graph classes with bounded tree-partition-width are exactly those that have bounded treewidth and satisfy a further ‘disjointedness’ condition. Furthermore, this result naturally generalises for
![]() $c$
-tree-partition-width and thus for underlying treewidth.
$c$
-tree-partition-width and thus for underlying treewidth.
3. Disjointed coverings
This section introduces disjointed coverings and shows that they can be used to characterise bounded
![]() $c$
-tree-partition-width and underlying treewidth (Theorem 11). On a high level, disjointed coverings are simply a weakening of
$c$
-tree-partition-width and underlying treewidth (Theorem 11). On a high level, disjointed coverings are simply a weakening of
![]() $c$
-tree-partitions. As such, they are often easier to construct than
$c$
-tree-partitions. As such, they are often easier to construct than
![]() $c$
-tree-partitions. This is important since disjointed coverings can in fact be used to construct
$c$
-tree-partitions. This is important since disjointed coverings can in fact be used to construct
![]() $c$
-tree-partitions (Lemma 8).
$c$
-tree-partitions (Lemma 8).
Here is the intuition behind disjointed coverings. An important property of any
![]() $c$
-tree
$c$
-tree
![]() $G$
is that for any set
$G$
is that for any set
![]() $S$
of
$S$
of
![]() $c+1$
vertices and any component
$c+1$
vertices and any component
![]() $X$
of
$X$
of
![]() $G-S$
, there is a set
$G-S$
, there is a set
![]() $Q$
of at most
$Q$
of at most
![]() $c$
vertices in
$c$
vertices in
![]() $X$
such that no component of
$X$
such that no component of
![]() $X-Q$
is adjacent to all of
$X-Q$
is adjacent to all of
![]() $S$
. Given a
$S$
. Given a
![]() $c$
-tree-partition of a graph, an analogous property holds for the parts of the partition. Weakening this property slightly and allowing the parts of the partition to overlap leads to the following definition of disjointed coverings.
$c$
-tree-partition of a graph, an analogous property holds for the parts of the partition. Weakening this property slightly and allowing the parts of the partition to overlap leads to the following definition of disjointed coverings.
An
![]() $\ell$
-covering of a graph
$\ell$
-covering of a graph
![]() $G$
is a set
$G$
is a set
![]() $\beta \subseteq 2^{V(G)}$
such that
$\beta \subseteq 2^{V(G)}$
such that
![]() $|B| \leqslant \ell$
for every
$|B| \leqslant \ell$
for every
![]() $B \in \beta$
, and
$B \in \beta$
, and
![]() $\cup \{B \,:\, B\in \beta \} = V(G)$
.Footnote
4
If
$\cup \{B \,:\, B\in \beta \} = V(G)$
.Footnote
4
If
![]() $B_1 \cap B_2 = \varnothing$
for all distinct
$B_1 \cap B_2 = \varnothing$
for all distinct
![]() $B_1,B_2 \in \beta$
, then
$B_1,B_2 \in \beta$
, then
![]() $\beta$
is an
$\beta$
is an
![]() $\ell$
-partition. As illustrated in Figure 1, an
$\ell$
-partition. As illustrated in Figure 1, an
![]() $\ell$
-covering
$\ell$
-covering
![]() $\beta$
of a graph
$\beta$
of a graph
![]() $G$
is
$G$
is
![]() $(c,d)$
-disjointed if for every
$(c,d)$
-disjointed if for every
![]() $c$
-tuple
$c$
-tuple
![]() $(B_1,\dots,B_c) \in \beta ^c$
and every component
$(B_1,\dots,B_c) \in \beta ^c$
and every component
![]() $X$
of
$X$
of
![]() $G-(B_1\cup \dots \cup B_c)$
there exists
$G-(B_1\cup \dots \cup B_c)$
there exists
![]() $Q \subseteq V(X)$
with
$Q \subseteq V(X)$
with
![]() $|Q| \leqslant d$
such that for each component
$|Q| \leqslant d$
such that for each component
![]() $Y$
of
$Y$
of
![]() $X-Q$
, for some
$X-Q$
, for some
![]() $i \in \{1,\dots,c\}$
we have
$i \in \{1,\dots,c\}$
we have
![]() $V(Y)\cap N_G\big(B^{\prime}_i\big) = \varnothing$
, where
$V(Y)\cap N_G\big(B^{\prime}_i\big) = \varnothing$
, where
![]() $B^{\prime}_i \,:\!=\, B_i\setminus (B_1 \cup \dotsb \cup B_{i-1})$
. Note that we can take
$B^{\prime}_i \,:\!=\, B_i\setminus (B_1 \cup \dotsb \cup B_{i-1})$
. Note that we can take
![]() $Q = \varnothing$
if some
$Q = \varnothing$
if some
![]() $B^{\prime}_i = \varnothing$
, since
$B^{\prime}_i = \varnothing$
, since
![]() $N_G(\varnothing ) = \varnothing$
.
$N_G(\varnothing ) = \varnothing$
.
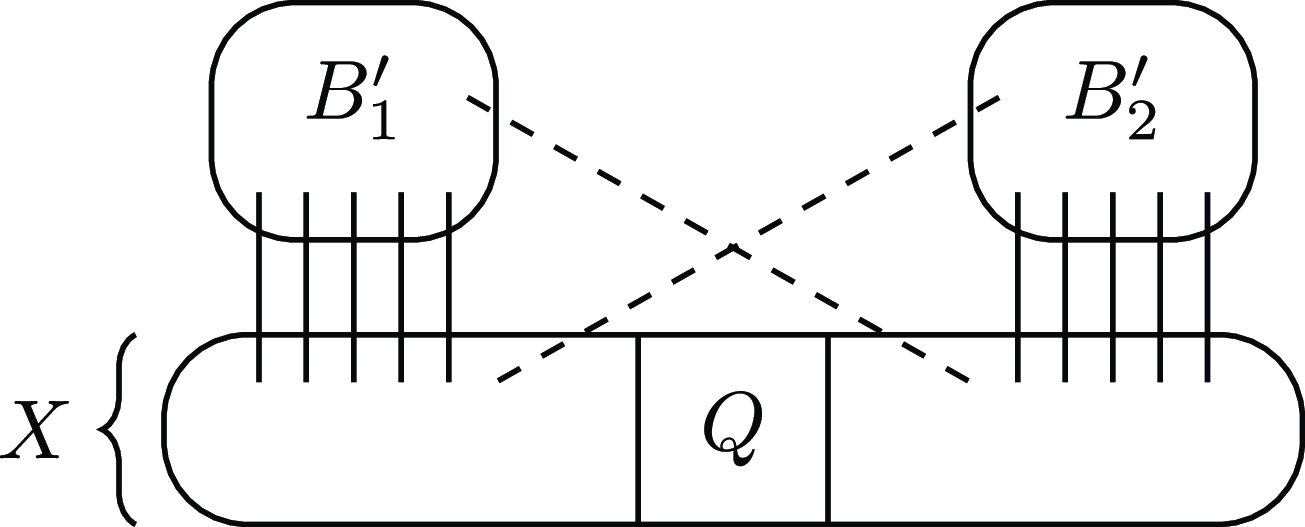
Figure 1. A disjointed partition with
![]() $c=2$
, where non-edges are dashed.
$c=2$
, where non-edges are dashed.
Let
![]() $\beta$
be an
$\beta$
be an
![]() $\ell$
-covering of a graph
$\ell$
-covering of a graph
![]() $G$
. For
$G$
. For
![]() $t \in{\mathbb{N}}$
, let
$t \in{\mathbb{N}}$
, let
![]() $\beta [t]$
$\beta [t]$
![]() $\,:\!=\, \{\bigcup \mathcal{B} \,:\, \mathcal{B}\subseteq \beta, |\mathcal{B}|\leqslant t\}$
. So
$\,:\!=\, \{\bigcup \mathcal{B} \,:\, \mathcal{B}\subseteq \beta, |\mathcal{B}|\leqslant t\}$
. So
![]() $\beta [t]$
is a
$\beta [t]$
is a
![]() $t\ell$
-covering of
$t\ell$
-covering of
![]() $G$
. For a function
$G$
. For a function
![]() $f \,:\,{\mathbb{N}} \to \mathbb{R}^+$
we say that
$f \,:\,{\mathbb{N}} \to \mathbb{R}^+$
we say that
![]() $\beta$
is
$\beta$
is
![]() $(c,f)$
-disjointed if
$(c,f)$
-disjointed if
![]() $\beta [t]$
is
$\beta [t]$
is
![]() $(c,f(t))$
-disjointed for every
$(c,f(t))$
-disjointed for every
![]() $t \in{\mathbb{N}}$
.
$t \in{\mathbb{N}}$
.
While
![]() $(c,d)$
-disjointed coverings are conceptually simpler than
$(c,d)$
-disjointed coverings are conceptually simpler than
![]() $(c,f)$
-disjointed coverings, we show they are roughly equivalent (Theorem 4). Moreover,
$(c,f)$
-disjointed coverings, we show they are roughly equivalent (Theorem 4). Moreover,
![]() $(c,f)$
-disjointed coverings are essential for the main proof (Lemma 8) and give better bounds on the
$(c,f)$
-disjointed coverings are essential for the main proof (Lemma 8) and give better bounds on the
![]() $c$
-tree-partition-width, leading to smaller treewidth-binding functions when determining the underlying treewidth of several graph classes of interest (for
$c$
-tree-partition-width, leading to smaller treewidth-binding functions when determining the underlying treewidth of several graph classes of interest (for
![]() $K_t$
-minor-free graphs for example).
$K_t$
-minor-free graphs for example).
Note that we often consider the singleton partition
![]() $\beta \,:\!=\, \{\{v\} \,:\, v \in V(G)\}$
of a graph
$\beta \,:\!=\, \{\{v\} \,:\, v \in V(G)\}$
of a graph
![]() $G$
, which is
$G$
, which is
![]() $(c,f)$
-disjointed if and only if, for every
$(c,f)$
-disjointed if and only if, for every
![]() $t \in{\mathbb{N}}$
, every
$t \in{\mathbb{N}}$
, every
![]() $t$
-partition of
$t$
-partition of
![]() $G$
is
$G$
is
![]() $(c,f(t))$
-disjointed.
$(c,f(t))$
-disjointed.
This section characterises
![]() $c$
-tree-partition-width in terms of
$c$
-tree-partition-width in terms of
![]() $(c,d)$
-disjointed coverings (or partitions) and
$(c,d)$
-disjointed coverings (or partitions) and
![]() $(c,f)$
-disjointed coverings (or partitions). The following observation deals with the
$(c,f)$
-disjointed coverings (or partitions). The following observation deals with the
![]() $c = 0$
case.
$c = 0$
case.
Observation 3.
The following are equivalent for any graph
![]() $G$
and
$G$
and
![]() $d \in{\mathbb{N}}$
:
$d \in{\mathbb{N}}$
:
-
(a)
 $G$
has a
$G$
has a
 $(0,d)$
-disjointed covering;
$(0,d)$
-disjointed covering;
-
(b) every covering of
 $G$
is
$G$
is
 $(0,d)$
-disjointed;
$(0,d)$
-disjointed;
-
(c) each component of
 $G$
has at most
$G$
has at most
 $d$
vertices;
$d$
vertices;
-
(d)
 $G$
has
$G$
has
 $0$
-tree-partition-width at most
$0$
-tree-partition-width at most
 $d$
.
$d$
.
Observation 3 implies that a graph class
![]() $\mathcal{G}$
has underlying treewidth
$\mathcal{G}$
has underlying treewidth
![]() $0$
if and only if there is a function
$0$
if and only if there is a function
![]() $f$
such that every component of every graph
$f$
such that every component of every graph
![]() $G \in \mathcal{G}$
has at most
$G \in \mathcal{G}$
has at most
![]() $f(\textrm{tw}(G))$
vertices.
$f(\textrm{tw}(G))$
vertices.
We prove the following characterisation of bounded
![]() $c$
-tree-partition-width (which is new even in the
$c$
-tree-partition-width (which is new even in the
![]() $c = 1$
case).
$c = 1$
case).
Theorem 4.
For fixed
![]() $c \in{\mathbb{N}}_0$
, the following are equivalent for a graph class
$c \in{\mathbb{N}}_0$
, the following are equivalent for a graph class
![]() $\mathcal{G}$
with bounded treewidth:
$\mathcal{G}$
with bounded treewidth:
-
(a)
 $\mathcal{G}$
has bounded
$\mathcal{G}$
has bounded
 $c$
-tree-partition-width;
$c$
-tree-partition-width;
-
(b) for some
 $d,\ell \in{\mathbb{N}}$
, every graph in
$d,\ell \in{\mathbb{N}}$
, every graph in
 $\mathcal{G}$
has a
$\mathcal{G}$
has a
 $(c,d)$
-disjointed
$(c,d)$
-disjointed
 $\ell$
-partition;
$\ell$
-partition;
-
(c) for some
 $d,\ell \in{\mathbb{N}}$
, every graph in
$d,\ell \in{\mathbb{N}}$
, every graph in
 $\mathcal{G}$
has a
$\mathcal{G}$
has a
 $(c,d)$
-disjointed
$(c,d)$
-disjointed
 $\ell$
-covering;
$\ell$
-covering;
-
(d) for some
 $\ell \in{\mathbb{N}}$
and function
$\ell \in{\mathbb{N}}$
and function
 $f$
, every graph in
$f$
, every graph in
 $\mathcal{G}$
has a
$\mathcal{G}$
has a
 $(c,f)$
-disjointed
$(c,f)$
-disjointed
 $\ell$
-partition;
$\ell$
-partition;
-
(e) for some
 $\ell \in{\mathbb{N}}$
and function
$\ell \in{\mathbb{N}}$
and function
 $f$
, every graph in
$f$
, every graph in
 $\mathcal{G}$
has a
$\mathcal{G}$
has a
 $(c,f)$
-disjointed
$(c,f)$
-disjointed
 $\ell$
-covering.
$\ell$
-covering.
Proof. Observation 3 handles the
![]() $c = 0$
case. Now assume that
$c = 0$
case. Now assume that
![]() $c \geqslant 1$
. Lemma 6 below says that (a) implies (b). Since every
$c \geqslant 1$
. Lemma 6 below says that (a) implies (b). Since every
![]() $\ell$
-partition is an
$\ell$
-partition is an
![]() $\ell$
-covering, (b) implies (c), and (d) implies (e). Lemma 5 below says that (c) implies (d). Finally, Lemma 8 below says that (e) implies (a).
$\ell$
-covering, (b) implies (c), and (d) implies (e). Lemma 5 below says that (c) implies (d). Finally, Lemma 8 below says that (e) implies (a).
By definition, every
![]() $(c,f)$
-disjointed
$(c,f)$
-disjointed
![]() $\ell$
-covering is
$\ell$
-covering is
![]() $(c,f(1))$
-disjointed. The next lemma gives a qualitative converse to this.
$(c,f(1))$
-disjointed. The next lemma gives a qualitative converse to this.
Lemma 5.
Let
![]() $\ell,c,d\in{\mathbb{N}}$
, and let
$\ell,c,d\in{\mathbb{N}}$
, and let
![]() $\beta$
be a
$\beta$
be a
![]() $(c,d)$
-disjointed
$(c,d)$
-disjointed
![]() $\ell$
-covering of a graph
$\ell$
-covering of a graph
![]() $G$
. Then
$G$
. Then
![]() $\beta$
is
$\beta$
is
![]() $(c,f)$
-disjointed, where
$(c,f)$
-disjointed, where
![]() $f(t) \,:\!=\, d t^c$
for each
$f(t) \,:\!=\, d t^c$
for each
![]() $t \in{\mathbb{N}}$
.
$t \in{\mathbb{N}}$
.
Proof. Fix
![]() $t \in{\mathbb{N}}$
. Let
$t \in{\mathbb{N}}$
. Let
![]() $B_1,\dots, B_c \in \beta [t]$
. Let
$B_1,\dots, B_c \in \beta [t]$
. Let
![]() $X$
be a component of
$X$
be a component of
![]() $G-(B_1\cup \dots \cup B_c)$
. For each
$G-(B_1\cup \dots \cup B_c)$
. For each
![]() $i\in \{1,\dots,c\}$
, let
$i\in \{1,\dots,c\}$
, let
![]() $\mathcal{B}_i$
be a set of at most
$\mathcal{B}_i$
be a set of at most
![]() $t$
elements of
$t$
elements of
![]() $\beta$
whose union is
$\beta$
whose union is
![]() $B_i$
. Let
$B_i$
. Let
![]() $\mathcal{F} \,:\!=\, \mathcal{B}_1 \times \dots \times \mathcal{B}_c$
, and for each
$\mathcal{F} \,:\!=\, \mathcal{B}_1 \times \dots \times \mathcal{B}_c$
, and for each
![]() $y = (A_1, \dots, A_c) \in \mathcal{F}$
, define
$y = (A_1, \dots, A_c) \in \mathcal{F}$
, define
![]() $Q_y$
as follows. Let
$Q_y$
as follows. Let
![]() $X_y$
the component of
$X_y$
the component of
![]() $G - (A_1 \cup \dots \cup A_c)$
containing
$G - (A_1 \cup \dots \cup A_c)$
containing
![]() $X$
. Since
$X$
. Since
![]() $\beta$
is
$\beta$
is
![]() $(c,d)$
-disjointed, there exists
$(c,d)$
-disjointed, there exists
![]() $Q_y \subseteq V(X_y)$
of size at most
$Q_y \subseteq V(X_y)$
of size at most
![]() $d$
such that for every component
$d$
such that for every component
![]() $Y$
of
$Y$
of
![]() $X_y-Q_y$
there is some
$X_y-Q_y$
there is some
![]() $i \in \{1, \dots, c\}$
such that
$i \in \{1, \dots, c\}$
such that
![]() $V(Y) \cap N_G(A_i \setminus (A_1 \cup \dots \cup A_{i-1})) = \varnothing$
. Now let
$V(Y) \cap N_G(A_i \setminus (A_1 \cup \dots \cup A_{i-1})) = \varnothing$
. Now let
![]() $Q \,:\!=\, \bigcup _{y \in \mathcal{F}} Q_y$
, and note that
$Q \,:\!=\, \bigcup _{y \in \mathcal{F}} Q_y$
, and note that
![]() $|Q|\leqslant d|\mathcal{F}| \leqslant dt^c$
.
$|Q|\leqslant d|\mathcal{F}| \leqslant dt^c$
.
Suppose for contradiction that for some component
![]() $Y$
of
$Y$
of
![]() $X - Q$
and each
$X - Q$
and each
![]() $i \in \{1,\dots, c\}$
, there is a vertex
$i \in \{1,\dots, c\}$
, there is a vertex
![]() $b_i \in N_G(Y) \cap B^{\prime}_i$
, where
$b_i \in N_G(Y) \cap B^{\prime}_i$
, where
![]() $B^{\prime}_i \,:\!=\, B_i \setminus (B_1 \cup \dots \cup B_{i-1})$
. Let
$B^{\prime}_i \,:\!=\, B_i \setminus (B_1 \cup \dots \cup B_{i-1})$
. Let
![]() $y = (A_1, \dots, A_c) \in \mathcal{F}$
be such that
$y = (A_1, \dots, A_c) \in \mathcal{F}$
be such that
![]() $(b_1, \dots, b_c) \in A_1 \times \dots \times A_c$
, and consider that component
$(b_1, \dots, b_c) \in A_1 \times \dots \times A_c$
, and consider that component
![]() $Y^{\prime}$
of
$Y^{\prime}$
of
![]() $X_y - Q_y$
containing
$X_y - Q_y$
containing
![]() $Y$
. By the definition of
$Y$
. By the definition of
![]() $Q_y$
, there is some
$Q_y$
, there is some
![]() $i \in \{1,\dots, c\}$
such that
$i \in \{1,\dots, c\}$
such that
![]() $Y^{\prime}$
contains no neighbour of a vertex in
$Y^{\prime}$
contains no neighbour of a vertex in
![]() $A_i \setminus (A_1 \cup \dots \cup A_{i-1})$
. In particular, all neighbours of vertices of
$A_i \setminus (A_1 \cup \dots \cup A_{i-1})$
. In particular, all neighbours of vertices of
![]() $Y$
are either vertices of
$Y$
are either vertices of
![]() $Y^{\prime}$
or neighbours of vertices of
$Y^{\prime}$
or neighbours of vertices of
![]() $Y^{\prime}$
, so
$Y^{\prime}$
, so
![]() $b_i$
is not a neighbour of any vertex of
$b_i$
is not a neighbour of any vertex of
![]() $Y$
, a contradiction.
$Y$
, a contradiction.
Now we prove that having a
![]() $(c,d)$
-disjointed partition is necessary for bounded
$(c,d)$
-disjointed partition is necessary for bounded
![]() $c$
-tree-partition-width.
$c$
-tree-partition-width.
Lemma 6.
For all
![]() $c,\ell \in{\mathbb{N}}_0$
, every graph
$c,\ell \in{\mathbb{N}}_0$
, every graph
![]() $G$
with
$G$
with
![]() $c$
-tree-partition-width
$c$
-tree-partition-width
![]() $\ell$
has a
$\ell$
has a
![]() $(c,c\ell )$
-disjointed
$(c,c\ell )$
-disjointed
![]() $\ell$
-partition.
$\ell$
-partition.
Proof. By assumption,
![]() $G$
has an
$G$
has an
![]() $H$
-partition
$H$
-partition
![]() $\beta = (V_h \,:\, h \in V(H))$
where
$\beta = (V_h \,:\, h \in V(H))$
where
![]() $H$
is a graph of treewidth at most
$H$
is a graph of treewidth at most
![]() $c$
and
$c$
and
![]() $|V_h| \leqslant \ell$
for all
$|V_h| \leqslant \ell$
for all
![]() $h$
. We first show that the singleton partition of
$h$
. We first show that the singleton partition of
![]() $H$
is
$H$
is
![]() $(c,c)$
-disjointed. Let
$(c,c)$
-disjointed. Let
![]() $v_1, \dotsc, v_c \in V(H)$
and let
$v_1, \dotsc, v_c \in V(H)$
and let
![]() $X$
be a component of
$X$
be a component of
![]() $H-\{v_1,\dots, v_c\}$
. Let
$H-\{v_1,\dots, v_c\}$
. Let
![]() $(W_x \,:\, x \in V(T))$
be a tree-decomposition of
$(W_x \,:\, x \in V(T))$
be a tree-decomposition of
![]() $H$
where
$H$
where
![]() $|W_x| \leqslant c + 1$
for all
$|W_x| \leqslant c + 1$
for all
![]() $x \in V(T)$
. We may assume that
$x \in V(T)$
. We may assume that
![]() $W_x \neq W_y$
whenever
$W_x \neq W_y$
whenever
![]() $x \neq y$
. For each
$x \neq y$
. For each
![]() $i \in \{1,\dots,c\}$
, let
$i \in \{1,\dots,c\}$
, let
![]() $T_i$
be the subtree of
$T_i$
be the subtree of
![]() $T$
induced by
$T$
induced by
![]() $\{x \in V(T) \,:\, v_i \in W_x\}$
.
$\{x \in V(T) \,:\, v_i \in W_x\}$
.
First suppose that
![]() $V(T_i) \cap V(T_j) = \varnothing$
for some
$V(T_i) \cap V(T_j) = \varnothing$
for some
![]() $i, j \in \{1,\dots,c\}$
. Let
$i, j \in \{1,\dots,c\}$
. Let
![]() $z \in V(T_i)$
be the closest node (in
$z \in V(T_i)$
be the closest node (in
![]() $T$
) to
$T$
) to
![]() $T_j$
. Let
$T_j$
. Let
![]() $Q \,:\!=\, W_z \cap X$
. Note that
$Q \,:\!=\, W_z \cap X$
. Note that
![]() $Q \subseteq W_z \setminus \{v_i\}$
so
$Q \subseteq W_z \setminus \{v_i\}$
so
![]() $|Q| \leqslant c$
. Any path from
$|Q| \leqslant c$
. Any path from
![]() $v_i$
to
$v_i$
to
![]() $v_j$
in
$v_j$
in
![]() $H$
passes through
$H$
passes through
![]() $W_z$
, so each component of
$W_z$
, so each component of
![]() $X - Q$
is disjoint from
$X - Q$
is disjoint from
![]() $N_H(v_i)$
or
$N_H(v_i)$
or
![]() $N_H(v_j)$
.
$N_H(v_j)$
.
Now assume that
![]() $V(T_i) \cap V(T_j) \neq \varnothing$
for all
$V(T_i) \cap V(T_j) \neq \varnothing$
for all
![]() $i, j\in \{1,\dots, c\}$
. Let
$i, j\in \{1,\dots, c\}$
. Let
![]() $T_X$
be the subgraph of
$T_X$
be the subgraph of
![]() $T$
induced by
$T$
induced by
![]() $\{x \in V(T) \,:\, V(X) \cap W_x \neq \varnothing \}$
. Since
$\{x \in V(T) \,:\, V(X) \cap W_x \neq \varnothing \}$
. Since
![]() $X$
is connected,
$X$
is connected,
![]() $T_X$
is a subtree of
$T_X$
is a subtree of
![]() $T$
. Suppose that
$T$
. Suppose that
![]() $V(T_i) \cap V(T_X) = \varnothing$
for some
$V(T_i) \cap V(T_X) = \varnothing$
for some
![]() $i$
. Since
$i$
. Since
![]() $N_H(v_i) \subseteq \bigcup (W_x \,:\, x \in V(T_i))$
, it follows that
$N_H(v_i) \subseteq \bigcup (W_x \,:\, x \in V(T_i))$
, it follows that
![]() $N_H(v_i) \cap V(X) = \varnothing$
and so we may take
$N_H(v_i) \cap V(X) = \varnothing$
and so we may take
![]() $Q \,:\!=\, \varnothing$
in this case. Now assume that
$Q \,:\!=\, \varnothing$
in this case. Now assume that
![]() $V(T_i) \cap V(T_X) \neq \varnothing$
for all
$V(T_i) \cap V(T_X) \neq \varnothing$
for all
![]() $i \in \{1,\dots,c\}$
. By the Helly property,
$i \in \{1,\dots,c\}$
. By the Helly property,
![]() $\tilde{T} \,:\!=\, T_1 \cap \dotsb \cap T_c \cap T_X$
is a non-empty subtree of
$\tilde{T} \,:\!=\, T_1 \cap \dotsb \cap T_c \cap T_X$
is a non-empty subtree of
![]() $T$
. For
$T$
. For
![]() $x \in V(\tilde{T})$
, we have
$x \in V(\tilde{T})$
, we have
![]() $|W_x| \leqslant c + 1$
and so
$|W_x| \leqslant c + 1$
and so
![]() $W_x = \{v_1, \dotsc, v_c, u\}$
for some
$W_x = \{v_1, \dotsc, v_c, u\}$
for some
![]() $u \in V(X)$
. First suppose that
$u \in V(X)$
. First suppose that
![]() $|V(\tilde{T})| \geqslant 2$
. Then there are adjacent
$|V(\tilde{T})| \geqslant 2$
. Then there are adjacent
![]() $x, y \in V(\tilde{T})$
with
$x, y \in V(\tilde{T})$
with
![]() $W_x = \{v_1, \dotsc, v_c, u\}$
and
$W_x = \{v_1, \dotsc, v_c, u\}$
and
![]() $W_y = \{v_1, \dotsc, v_c, v\}$
for
$W_y = \{v_1, \dotsc, v_c, v\}$
for
![]() $u, v \in V(X)$
. Since
$u, v \in V(X)$
. Since
![]() $W_x \neq W_y$
, we have
$W_x \neq W_y$
, we have
![]() $u \neq v$
and thus there is no
$u \neq v$
and thus there is no
![]() $(u,v)$
-path in
$(u,v)$
-path in
![]() $H - \{v_1, \dotsc, v_c\}$
, contradicting the connectedness of
$H - \{v_1, \dotsc, v_c\}$
, contradicting the connectedness of
![]() $X$
. Hence
$X$
. Hence
![]() $\tilde{T}$
consists of a single vertex
$\tilde{T}$
consists of a single vertex
![]() $z$
; thus
$z$
; thus
![]() $W_z = \{v_1, \dotsc, v_c, u\}$
for some
$W_z = \{v_1, \dotsc, v_c, u\}$
for some
![]() $u \in V(X)$
. Let
$u \in V(X)$
. Let
![]() $Q \,:\!=\, \{u\}$
and consider a component
$Q \,:\!=\, \{u\}$
and consider a component
![]() $Y$
of
$Y$
of
![]() $X - Q$
. Let
$X - Q$
. Let
![]() $T_{Y}$
be the subtree of
$T_{Y}$
be the subtree of
![]() $T$
induced by
$T$
induced by
![]() $\{y\in V(T) \,:\, V(Y) \cap W_y \neq \varnothing \}$
. Since
$\{y\in V(T) \,:\, V(Y) \cap W_y \neq \varnothing \}$
. Since
![]() $T_{Y}$
is connected and does not contain
$T_{Y}$
is connected and does not contain
![]() $z$
, it is disjoint from some
$z$
, it is disjoint from some
![]() $T_i$
. As above,
$T_i$
. As above,
![]() $N_H(v_i) \cap V(Y) = \varnothing$
, as required.
$N_H(v_i) \cap V(Y) = \varnothing$
, as required.
We have shown that the singleton partition of
![]() $H$
is
$H$
is
![]() $(c,c)$
-disjointed. Now focus on
$(c,c)$
-disjointed. Now focus on
![]() $G$
. By assumption,
$G$
. By assumption,
![]() $\beta$
is an
$\beta$
is an
![]() $\ell$
-partition of
$\ell$
-partition of
![]() $G$
. Let
$G$
. Let
![]() $V_{v_1}, \dotsc, V_{v_c}$
be parts in
$V_{v_1}, \dotsc, V_{v_c}$
be parts in
![]() $\beta$
, and let
$\beta$
, and let
![]() $X$
be a component of
$X$
be a component of
![]() $G - (V_{v_1} \cup \dotsb \cup V_{v_c})$
. Then
$G - (V_{v_1} \cup \dotsb \cup V_{v_c})$
. Then
![]() $X \subseteq \bigcup \{V_h \,:\, h \in X^{\prime}\}$
where
$X \subseteq \bigcup \{V_h \,:\, h \in X^{\prime}\}$
where
![]() $X^{\prime}$
is a component of
$X^{\prime}$
is a component of
![]() $H - \{v_1, \dotsc, v_c\}$
. Since
$H - \{v_1, \dotsc, v_c\}$
. Since
![]() $H$
is
$H$
is
![]() $(c,c)$
-disjointed, there exists
$(c,c)$
-disjointed, there exists
![]() $Q^{\prime} \subseteq V(X^{\prime})$
of size at most
$Q^{\prime} \subseteq V(X^{\prime})$
of size at most
![]() $c$
such that each component
$c$
such that each component
![]() $X^{\prime} - Q^{\prime}$
is disjoint from some
$X^{\prime} - Q^{\prime}$
is disjoint from some
![]() $N_H(v_i)$
. Let
$N_H(v_i)$
. Let
![]() $Q \,:\!=\, \bigcup \{V_h \,:\, h \in Q^{\prime}\}$
, which has size at most
$Q \,:\!=\, \bigcup \{V_h \,:\, h \in Q^{\prime}\}$
, which has size at most
![]() $c\ell$
. Each component of
$c\ell$
. Each component of
![]() $X - Q$
is disjoint from some
$X - Q$
is disjoint from some
![]() $N_G(V_{v_i})$
.
$N_G(V_{v_i})$
.
Note that
![]() $(c, f)$
-disjointedness is preserved when restricting to a subgraph.
$(c, f)$
-disjointedness is preserved when restricting to a subgraph.
Lemma 7.
If
![]() $\beta$
is a
$\beta$
is a
![]() $(c,f)$
-disjointed
$(c,f)$
-disjointed
![]() $\ell$
-covering of a graph
$\ell$
-covering of a graph
![]() $G$
, then for every subgraph
$G$
, then for every subgraph
![]() $\tilde{G}$
of
$\tilde{G}$
of
![]() $G$
, the restriction
$G$
, the restriction
![]() $\tilde{\beta } \,:\!=\, \{ B \cap V(\tilde{G}) \,:\, B \in \beta \}$
is a
$\tilde{\beta } \,:\!=\, \{ B \cap V(\tilde{G}) \,:\, B \in \beta \}$
is a
![]() $(c,f)$
-disjointed
$(c,f)$
-disjointed
![]() $\ell$
-covering of
$\ell$
-covering of
![]() $\tilde{G}$
.
$\tilde{G}$
.
Proof. Fix
![]() $t \in{\mathbb{N}}$
. Let
$t \in{\mathbb{N}}$
. Let
![]() $\tilde{B}_1, \dots, \tilde{B}_c \in \tilde{\beta }[t]$
and let
$\tilde{B}_1, \dots, \tilde{B}_c \in \tilde{\beta }[t]$
and let
![]() $\tilde{X}$
be a component of
$\tilde{X}$
be a component of
![]() $\tilde{G}-\big(\tilde{B}_1\cup \dots \cup \tilde{B}_c\big)$
. For each
$\tilde{G}-\big(\tilde{B}_1\cup \dots \cup \tilde{B}_c\big)$
. For each
![]() $i \in \{1,\dots, c\}$
, there is a subset
$i \in \{1,\dots, c\}$
, there is a subset
![]() $S_i \subseteq \beta$
of size at most
$S_i \subseteq \beta$
of size at most
![]() $t$
such that
$t$
such that
![]() $\tilde{B}_i = \bigcup _{B \in S_i} (B\cap V(\tilde{G}))$
. Let
$\tilde{B}_i = \bigcup _{B \in S_i} (B\cap V(\tilde{G}))$
. Let
![]() $(B_1,\dots,B_c)\,:\!=\, (\bigcup S_1,\dots,\bigcup S_c)$
, and let
$(B_1,\dots,B_c)\,:\!=\, (\bigcup S_1,\dots,\bigcup S_c)$
, and let
![]() $\beta^{\prime\prime}$
be the
$\beta^{\prime\prime}$
be the
![]() $t\ell$
-covering of
$t\ell$
-covering of
![]() $G$
given by
$G$
given by
![]() $\beta \cup \{B_1,\dots,B_c\}$
. Let
$\beta \cup \{B_1,\dots,B_c\}$
. Let
![]() $X$
be the component of
$X$
be the component of
![]() ${G-(B_1\cup \dots \cup B_c})$
which contains
${G-(B_1\cup \dots \cup B_c})$
which contains
![]() $\tilde{X}$
, and for each
$\tilde{X}$
, and for each
![]() $i \in \{1,\dots, c\}$
let
$i \in \{1,\dots, c\}$
let
![]() $B^{\prime}_i\,:\!=\, B_i\setminus (B_1\cup \dots \cup B_{i-1})$
. Since
$B^{\prime}_i\,:\!=\, B_i\setminus (B_1\cup \dots \cup B_{i-1})$
. Since
![]() $\beta$
is
$\beta$
is
![]() $(c,f)$
-disjointed, there is a subset
$(c,f)$
-disjointed, there is a subset
![]() $Q$
of
$Q$
of
![]() $V(X)$
of size at most
$V(X)$
of size at most
![]() $f(t)$
such that each component of
$f(t)$
such that each component of
![]() $X-Q$
disjoint from
$X-Q$
disjoint from
![]() $N_G\big(B^{\prime}_i\big)$
for some
$N_G\big(B^{\prime}_i\big)$
for some
![]() $i \in \{1,\dots,c\}$
. Let
$i \in \{1,\dots,c\}$
. Let
![]() $\tilde{Q}\,:\!=\, Q\cap V(\tilde{X})$
, and note that
$\tilde{Q}\,:\!=\, Q\cap V(\tilde{X})$
, and note that
![]() $|\tilde{Q}|\leqslant |Q|\leqslant f(t)$
. Each component of
$|\tilde{Q}|\leqslant |Q|\leqslant f(t)$
. Each component of
![]() $\tilde{X}-\tilde{Q}$
is contained in a component of
$\tilde{X}-\tilde{Q}$
is contained in a component of
![]() $X - Q$
, and hence is disjoint from
$X - Q$
, and hence is disjoint from
![]() $N_{\tilde{G}}\big(\tilde{B}_i\setminus \big(\tilde{B}_1\cup \dots \cup \tilde{B}_{i-1}\big)\big)\subseteq N_G\big(B^{\prime}_i\big)$
for some
$N_{\tilde{G}}\big(\tilde{B}_i\setminus \big(\tilde{B}_1\cup \dots \cup \tilde{B}_{i-1}\big)\big)\subseteq N_G\big(B^{\prime}_i\big)$
for some
![]() $i \in \{1,\dots, c\}$
. Hence
$i \in \{1,\dots, c\}$
. Hence
![]() $\tilde{\beta }$
is
$\tilde{\beta }$
is
![]() $(c,f)$
-disjointed.
$(c,f)$
-disjointed.
The next lemma lies at the heart of the paper.
Lemma 8.
Let
![]() $k,c,\ell \in{\mathbb{N}}$
and
$k,c,\ell \in{\mathbb{N}}$
and
![]() $f \,:\,{\mathbb{N}} \to \mathbb{R}^+$
. For any graph
$f \,:\,{\mathbb{N}} \to \mathbb{R}^+$
. For any graph
![]() $G$
, if
$G$
, if
![]() $\textrm{tw}(G)\lt k$
and
$\textrm{tw}(G)\lt k$
and
![]() $G$
has a
$G$
has a
![]() $(c,f)$
-disjointed
$(c,f)$
-disjointed
![]() $\ell$
-covering, then
$\ell$
-covering, then
![]() $G$
has
$G$
has
![]() $c$
-tree-partition-width
$c$
-tree-partition-width
![]() $\textrm{tpw}_c(G) \leqslant \max \{ 12\ell k, 2 c \ell f(12 k)\}$
.
$\textrm{tpw}_c(G) \leqslant \max \{ 12\ell k, 2 c \ell f(12 k)\}$
.
We prove Lemma 8 via the following induction hypothesis.
Lemma 9.
Let
![]() $k,c,\ell \in{\mathbb{N}}$
and let
$k,c,\ell \in{\mathbb{N}}$
and let
![]() $f \,:\,{\mathbb{N}} \to \mathbb{R}^+$
. Let
$f \,:\,{\mathbb{N}} \to \mathbb{R}^+$
. Let
![]() $G$
be a graph of treewidth less than
$G$
be a graph of treewidth less than
![]() $k$
and let
$k$
and let
![]() $\beta \subseteq 2^{V(G)}$
be a
$\beta \subseteq 2^{V(G)}$
be a
![]() $(c,f)$
-disjointed
$(c,f)$
-disjointed
![]() $\ell$
-covering of
$\ell$
-covering of
![]() $G$
. Let
$G$
. Let
![]() $S_1, \dotsc, S_{c - 1}, R \subseteq V(G)$
, where
$S_1, \dotsc, S_{c - 1}, R \subseteq V(G)$
, where
![]() $S_i \in \beta [12k]$
for each
$S_i \in \beta [12k]$
for each
![]() $i \in \{1, \dotsc, c - 1\}$
and
$i \in \{1, \dotsc, c - 1\}$
and
![]() $4 k\leqslant |R| \leqslant f(12 k)$
. Then there exists a
$4 k\leqslant |R| \leqslant f(12 k)$
. Then there exists a
![]() $c$
-tree-partition
$c$
-tree-partition
![]() $(V_x \,:\, x \in V(H))$
of
$(V_x \,:\, x \in V(H))$
of
![]() $G$
of width at most
$G$
of width at most
![]() $W \,:\!=\, \max \{ 12\ell k, 2 c \ell f(12 k) \}$
, and there exists a
$W \,:\!=\, \max \{ 12\ell k, 2 c \ell f(12 k) \}$
, and there exists a
![]() $c$
-clique
$c$
-clique
![]() $\{x_1,\dots,x_{c-1},y\}$
of
$\{x_1,\dots,x_{c-1},y\}$
of
![]() $H$
such that
$H$
such that
![]() $V_{x_i} = S_i\setminus (S_1\cup \dots \cup S_{i-1})$
for each
$V_{x_i} = S_i\setminus (S_1\cup \dots \cup S_{i-1})$
for each
![]() $i \in \{1,\dots,c-1\}$
, and
$i \in \{1,\dots,c-1\}$
, and
![]() $R \setminus (S_1 \cup \dots \cup S_{c - 1}) \subseteq V_y$
with
$R \setminus (S_1 \cup \dots \cup S_{c - 1}) \subseteq V_y$
with
![]() $|V_y| \leqslant 2 \ell (|R| - 2 k)$
.
$|V_y| \leqslant 2 \ell (|R| - 2 k)$
.
Proof. We proceed by induction on
![]() $|V(G)|$
. Let
$|V(G)|$
. Let
![]() $S \,:\!=\, S_1 \cup \dotsb \cup S_{c - 1}$
.
$S \,:\!=\, S_1 \cup \dotsb \cup S_{c - 1}$
.
Case 0.
![]() $V(G) = R \cup S$
: Let
$V(G) = R \cup S$
: Let
![]() $H$
be the complete graph on vertices
$H$
be the complete graph on vertices
![]() $x_1, \dotsc, x_{c - 1}, y$
. Let
$x_1, \dotsc, x_{c - 1}, y$
. Let
![]() $V_{x_i} \,:\!=\, S_i \setminus (S_1 \cup \dotsb \cup S_{i - 1})$
for each
$V_{x_i} \,:\!=\, S_i \setminus (S_1 \cup \dotsb \cup S_{i - 1})$
for each
![]() $i$
and let
$i$
and let
![]() $V_y \,:\!=\, R$
. Then
$V_y \,:\!=\, R$
. Then
![]() $(V_x \,:\, x \in V(H))$
is a
$(V_x \,:\, x \in V(H))$
is a
![]() $c$
-tree-partition of
$c$
-tree-partition of
![]() $G$
with width at most
$G$
with width at most
![]() $W$
and
$W$
and
![]() $|V_y| = |R| \leqslant 2(|R| - 2k) \leqslant 2 \ell (|R| - 2k)$
. From now on assume that
$|V_y| = |R| \leqslant 2(|R| - 2k) \leqslant 2 \ell (|R| - 2k)$
. From now on assume that
![]() $G - (R \cup S)$
is non-empty.
$G - (R \cup S)$
is non-empty.
Case 1.
![]() $4 k \leqslant |R|\leqslant 12 k$
: Since
$4 k \leqslant |R|\leqslant 12 k$
: Since
![]() $\beta$
is an
$\beta$
is an
![]() $\ell$
-covering, and
$\ell$
-covering, and
![]() $|R| \leqslant 12k$
, we can pick
$|R| \leqslant 12k$
, we can pick
![]() $S_c \in \beta [12k]$
such that
$S_c \in \beta [12k]$
such that
![]() $R \subseteq S_c$
and
$R \subseteq S_c$
and
![]() $|S_c| \leqslant \ell |R| \leqslant 2 \ell (|R| - 2k)$
.
$|S_c| \leqslant \ell |R| \leqslant 2 \ell (|R| - 2k)$
.
Let
![]() $G_1, \dotsc, G_a$
be the connected components of
$G_1, \dotsc, G_a$
be the connected components of
![]() $G - (S \cup S_c)$
. For each
$G - (S \cup S_c)$
. For each
![]() $i \in \{1,\dots,c\}$
, let
$i \in \{1,\dots,c\}$
, let
![]() $S^{\prime}_i \,:\!=\, S_i \setminus (S_1 \cup \dotsb \cup S_{i - 1})$
. To complete this case, we first prove the following.
$S^{\prime}_i \,:\!=\, S_i \setminus (S_1 \cup \dotsb \cup S_{i - 1})$
. To complete this case, we first prove the following.
Figure 2. The graphs
![]() $F_1$
and
$F_1$
and
![]() $F_2$
in the case
$F_2$
in the case
![]() $c=2$
.
$c=2$
.
Claim 1.
For each
![]() $j \in \{1,\dots,a\}$
, the subgraph
$j \in \{1,\dots,a\}$
, the subgraph
![]() $G[ V(G_j) \cup S \cup S_c ]$
has a
$G[ V(G_j) \cup S \cup S_c ]$
has a
![]() $c$
-tree-partition
$c$
-tree-partition
![]() $\big(V_h^j \,:\, h \in V(H_j)\big)$
of width at most
$\big(V_h^j \,:\, h \in V(H_j)\big)$
of width at most
![]() $W$
such that there is a
$W$
such that there is a
![]() $c$
-clique
$c$
-clique
![]() $K = \{x_1, \dotsc, x_c\}$
in
$K = \{x_1, \dotsc, x_c\}$
in
![]() $H_j$
, where
$H_j$
, where
![]() $S^{\prime}_i = V^j_{x_i}$
for each
$S^{\prime}_i = V^j_{x_i}$
for each
![]() $i \in \{1,\dots,c\}$
.
$i \in \{1,\dots,c\}$
.
Proof. If
![]() $|V(G_j)| \lt 4 k$
, then take
$|V(G_j)| \lt 4 k$
, then take
![]() $H_j$
to be the complete graph on vertices
$H_j$
to be the complete graph on vertices
![]() $x_1, \dotsc, x_{c}, z$
with the partition
$x_1, \dotsc, x_{c}, z$
with the partition
![]() $V^j_{x_i} \,:\!=\, S^{\prime}_i$
for
$V^j_{x_i} \,:\!=\, S^{\prime}_i$
for
![]() $i \in \{1,\dots,c\}$
and
$i \in \{1,\dots,c\}$
and
![]() $V^j_{z} \,:\!=\, V(G_j)$
. Then this gives us the desired
$V^j_{z} \,:\!=\, V(G_j)$
. Then this gives us the desired
![]() $c$
-tree-partition of
$c$
-tree-partition of
![]() $G[V(G_j) \cup S \cup S_c]$
. So assume
$G[V(G_j) \cup S \cup S_c]$
. So assume
![]() $|V(G_j)| \geqslant 4k$
. Note that
$|V(G_j)| \geqslant 4k$
. Note that
![]() $\beta [12k]$
is a
$\beta [12k]$
is a
![]() $(c,f(12 k))$
-disjointed
$(c,f(12 k))$
-disjointed
![]() $12k\ell$
-covering containing
$12k\ell$
-covering containing
![]() $S_1, \dots, S_c$
, so there is a subset
$S_1, \dots, S_c$
, so there is a subset
![]() $Q^{\prime}_j \subseteq V(G_j)$
of size at most
$Q^{\prime}_j \subseteq V(G_j)$
of size at most
![]() $f(12 k)$
and there is a partition
$f(12 k)$
and there is a partition
![]() $\{A_1, \dotsc, A_c\}$
of
$\{A_1, \dotsc, A_c\}$
of
![]() $V\big(G_j - Q^{\prime}_j\big)$
such that each
$V\big(G_j - Q^{\prime}_j\big)$
such that each
![]() $A_i$
is a union of vertex sets of components of
$A_i$
is a union of vertex sets of components of
![]() $G_j - Q^{\prime}_j$
that do not intersect
$G_j - Q^{\prime}_j$
that do not intersect
![]() $N_{G}\big(S^{\prime}_i\big)$
. Let
$N_{G}\big(S^{\prime}_i\big)$
. Let
![]() $Q_j$
be a set such that
$Q_j$
be a set such that
![]() $Q^{\prime}_j \subseteq Q_j \subseteq V(G_j)$
and
$Q^{\prime}_j \subseteq Q_j \subseteq V(G_j)$
and
![]() $4k \leqslant |Q_j| \leqslant f(12 k)$
. As illustrated in Figure 2, consider the subgraph
$4k \leqslant |Q_j| \leqslant f(12 k)$
. As illustrated in Figure 2, consider the subgraph
By Lemma 7, the restriction of
![]() $\beta$
to
$\beta$
to
![]() $V(F_i)$
is a
$V(F_i)$
is a
![]() $(c,f)$
-disjointed
$(c,f)$
-disjointed
![]() $\ell$
-covering of
$\ell$
-covering of
![]() $F_i$
. Apply induction to
$F_i$
. Apply induction to
![]() $F_i$
with the sets
$F_i$
with the sets
![]() $S_1,\dotsc,S_{i - 1},S_{i + 1} \setminus S^{\prime}_i,\dotsc,S_c\setminus S^{\prime}_i$
in place of the sets
$S_1,\dotsc,S_{i - 1},S_{i + 1} \setminus S^{\prime}_i,\dotsc,S_c\setminus S^{\prime}_i$
in place of the sets
![]() $S_1,\dotsc,S_{c-1}$
and the set
$S_1,\dotsc,S_{c-1}$
and the set
![]() $Q_{j}$
in the place of
$Q_{j}$
in the place of
![]() $R$
. For each
$R$
. For each
![]() $i \in \{1,\dotsc,c\}$
, this gives a graph
$i \in \{1,\dotsc,c\}$
, this gives a graph
![]() $L_i$
of treewidth at most
$L_i$
of treewidth at most
![]() $c$
containing a
$c$
containing a
![]() $c$
-clique
$c$
-clique
![]() $\{x_1, \dotsc, x_{i-1}, x_{i+1},\dotsc, x_c, y\}$
such that
$\{x_1, \dotsc, x_{i-1}, x_{i+1},\dotsc, x_c, y\}$
such that
![]() $F_i$
has an
$F_i$
has an
![]() $L_i$
-partition
$L_i$
-partition
![]() $\big( V^{j,i}_x \,:\, x \in V(L_i) \big)$
with
$\big( V^{j,i}_x \,:\, x \in V(L_i) \big)$
with
![]() $V^{j,i}_{x_m} = S^{\prime}_m$
for all
$V^{j,i}_{x_m} = S^{\prime}_m$
for all
![]() $m \in \{1,\dots, i-1,i+1,\dots, c\}$
and
$m \in \{1,\dots, i-1,i+1,\dots, c\}$
and
![]() $Q_j \setminus \big((S\cup S_c) \setminus S^{\prime}_i)\big) \subseteq V_y^{j,i}$
where
$Q_j \setminus \big((S\cup S_c) \setminus S^{\prime}_i)\big) \subseteq V_y^{j,i}$
where
Let
![]() $L_i^+$
be
$L_i^+$
be
![]() $L_i$
together with a vertex
$L_i$
together with a vertex
![]() $x_i$
adjacent to the clique
$x_i$
adjacent to the clique
![]() $\{x_1, \dotsc, x_{i - 1}, x_{i + 1}, \dotsc, x_c, y\}$
. So
$\{x_1, \dotsc, x_{i - 1}, x_{i + 1}, \dotsc, x_c, y\}$
. So
![]() $\textrm{tw}(L^+_i)\leqslant c$
. Set
$\textrm{tw}(L^+_i)\leqslant c$
. Set
![]() $V^{j,i}_{x_i} \,:\!=\, S^{\prime}_i$
. Then
$V^{j,i}_{x_i} \,:\!=\, S^{\prime}_i$
. Then
![]() $L^+_i$
contains the
$L^+_i$
contains the
![]() $(c + 1)$
-clique
$(c + 1)$
-clique
![]() $K^+ \,:\!=\, \{x_1, \dotsc, x_c, y\}$
and
$K^+ \,:\!=\, \{x_1, \dotsc, x_c, y\}$
and
![]() $\big(V^{j,i}_h \,:\, h \in V(L^+_i)\big)$
is an
$\big(V^{j,i}_h \,:\, h \in V(L^+_i)\big)$
is an
![]() $L^+_i$
-partition of
$L^+_i$
-partition of
![]() $G[A_i \cup Q_j \cup S \cup S_c]$
. Now we may assume that
$G[A_i \cup Q_j \cup S \cup S_c]$
. Now we may assume that
![]() $V(L^+_1), \dotsc, V(L^+_c)$
pairwise intersect in exactly the clique
$V(L^+_1), \dotsc, V(L^+_c)$
pairwise intersect in exactly the clique
![]() $K^+$
. Let
$K^+$
. Let
![]() $H_j \,:\!=\, L_1^+\cup \dots \cup L_c^+$
. Since each
$H_j \,:\!=\, L_1^+\cup \dots \cup L_c^+$
. Since each
![]() $L_i^+$
has treewidth at most
$L_i^+$
has treewidth at most
![]() $c$
, so does
$c$
, so does
![]() $H_j$
. For
$H_j$
. For
![]() $x \notin K^+$
, set
$x \notin K^+$
, set
![]() $V^j_x \,:\!=\, V^{j,i}_x$
for the unique
$V^j_x \,:\!=\, V^{j,i}_x$
for the unique
![]() $i$
for which
$i$
for which
![]() $x \in V(L_i^+)$
, for
$x \in V(L_i^+)$
, for
![]() $i \in \{1, \dotsc, c \}$
set
$i \in \{1, \dotsc, c \}$
set
![]() $V^j_{x_i} \,:\!=\, S^{\prime}_i$
, and set
$V^j_{x_i} \,:\!=\, S^{\prime}_i$
, and set
![]() $V^j_y \,:\!=\, \bigcup _{i \in \{1, \dotsc, c\}} V^{j,i}_y$
. Since
$V^j_y \,:\!=\, \bigcup _{i \in \{1, \dotsc, c\}} V^{j,i}_y$
. Since
![]() $|V^{j}_y| \leqslant 2c \ell f(12 k)$
, the partition
$|V^{j}_y| \leqslant 2c \ell f(12 k)$
, the partition
![]() $\big( V^j_x \,:\, x \in V(H_j) \big)$
has width at most
$\big( V^j_x \,:\, x \in V(H_j) \big)$
has width at most
![]() $W$
. Setting
$W$
. Setting
![]() $K \,:\!=\, \{ x_1 \dotsc, x_c \}$
, the claim follows.
$K \,:\!=\, \{ x_1 \dotsc, x_c \}$
, the claim follows.
We may assume that
![]() $V(H_1), \dotsc, V(H_a)$
pairwise intersect in exactly the clique
$V(H_1), \dotsc, V(H_a)$
pairwise intersect in exactly the clique
![]() $K$
. Let
$K$
. Let
![]() $H \,:\!=\,{H_1\cup \dotsc \cup H_a}$
. For
$H \,:\!=\,{H_1\cup \dotsc \cup H_a}$
. For
![]() $x \in V(H)$
, setting
$x \in V(H)$
, setting
![]() $V_x \,:\!=\, V^j_x$
if
$V_x \,:\!=\, V^j_x$
if
![]() $x \in V(H_j)$
is well defined, and yields an
$x \in V(H_j)$
is well defined, and yields an
![]() $H$
-partition
$H$
-partition
![]() $(V_h \,:\, h \in V(H))$
of
$(V_h \,:\, h \in V(H))$
of
![]() $G$
. Since each
$G$
. Since each
![]() $H_i$
has treewidth at most
$H_i$
has treewidth at most
![]() $c$
, so does
$c$
, so does
![]() $H$
. Let
$H$
. Let
![]() $y \,:\!=\, x_c$
. Then
$y \,:\!=\, x_c$
. Then
![]() $R \setminus S \subseteq S^{\prime}_c = V_{y}$
, and, as noted at the start of this case,
$R \setminus S \subseteq S^{\prime}_c = V_{y}$
, and, as noted at the start of this case,
![]() $|V_{y}| = |S^{\prime}_c| \leqslant |S_c| \leqslant 2 \ell (|R| - 2k)$
. Hence, the width of this partition is at most
$|V_{y}| = |S^{\prime}_c| \leqslant |S_c| \leqslant 2 \ell (|R| - 2k)$
. Hence, the width of this partition is at most
![]() $W$
, as required.
$W$
, as required.
Case 2.
![]() $12 k \lt |R| \leqslant f(12 k)$
: Since
$12 k \lt |R| \leqslant f(12 k)$
: Since
![]() $\textrm{tw}(G) \lt k$
, by the separator lemma of Robertson and Seymour [Reference Robertson and Seymour65, (2.6)], there is a partition
$\textrm{tw}(G) \lt k$
, by the separator lemma of Robertson and Seymour [Reference Robertson and Seymour65, (2.6)], there is a partition
![]() $(A, B, C)$
of
$(A, B, C)$
of
![]() $V(G)$
with no edges between
$V(G)$
with no edges between
![]() $A$
and
$A$
and
![]() $B$
, where
$B$
, where
![]() $|C| \leqslant k$
and
$|C| \leqslant k$
and
![]() $|A \cap R|, |B \cap R| \leqslant \tfrac{2}{3} |R \setminus C|$
. Let
$|A \cap R|, |B \cap R| \leqslant \tfrac{2}{3} |R \setminus C|$
. Let
![]() $G_1 \,:\!=\, G[A \cup C]$
and
$G_1 \,:\!=\, G[A \cup C]$
and
![]() $G_2 \,:\!=\, G[B \cup C]$
. Let
$G_2 \,:\!=\, G[B \cup C]$
. Let
![]() $R_1 \,:\!=\, (R \cap A) \cup C$
and
$R_1 \,:\!=\, (R \cap A) \cup C$
and
![]() $R_2 \,:\!=\, (R \cap B) \cup C$
. Since
$R_2 \,:\!=\, (R \cap B) \cup C$
. Since
![]() $|R| \geqslant 12 k$
,
$|R| \geqslant 12 k$
,
 \begin{align*} |R_1| & = |A \cap R| + |C| \leqslant \tfrac{2}{3} |R| + k \lt |R| \quad \textrm{and}\\ |R_1| & \geqslant |R| - |B \cap R| \geqslant |R| - \tfrac{2}{3} |R \setminus C| \geqslant \tfrac{1}{3}|R|\geqslant 4k. \end{align*}
\begin{align*} |R_1| & = |A \cap R| + |C| \leqslant \tfrac{2}{3} |R| + k \lt |R| \quad \textrm{and}\\ |R_1| & \geqslant |R| - |B \cap R| \geqslant |R| - \tfrac{2}{3} |R \setminus C| \geqslant \tfrac{1}{3}|R|\geqslant 4k. \end{align*}
Hence,
![]() $4 k \leqslant |R_1| \leqslant f(12k)$
and similarly
$4 k \leqslant |R_1| \leqslant f(12k)$
and similarly
![]() $4 k \leqslant |R_2| \leqslant f(12k)$
. Also
$4 k \leqslant |R_2| \leqslant f(12k)$
. Also
![]() $|V(G) - V(G_1)| = |B| \geqslant |R_2| - |C| \geqslant 4k - k \gt 0$
, so
$|V(G) - V(G_1)| = |B| \geqslant |R_2| - |C| \geqslant 4k - k \gt 0$
, so
![]() $|V(G_1)| \lt |V(G)|$
and likewise for
$|V(G_1)| \lt |V(G)|$
and likewise for
![]() $G_2$
. Fix
$G_2$
. Fix
![]() $j \in \{1, 2\}$
. Let
$j \in \{1, 2\}$
. Let
![]() $\beta _j$
be the restriction of
$\beta _j$
be the restriction of
![]() $\beta$
to
$\beta$
to
![]() $V(G_j)$
. By Lemma 7,
$V(G_j)$
. By Lemma 7,
![]() $\beta _j$
is a
$\beta _j$
is a
![]() $(c, f)$
-disjointed
$(c, f)$
-disjointed
![]() $\ell$
-covering of
$\ell$
-covering of
![]() $G_j$
. Let
$G_j$
. Let
![]() $S^j_i \,:\!=\, S_i \cap V(G_j)$
for each
$S^j_i \,:\!=\, S_i \cap V(G_j)$
for each
![]() $i \in \{1,\dots,c-1\}$
; note that each set
$i \in \{1,\dots,c-1\}$
; note that each set
![]() $S^j_i$
is a union of at most
$S^j_i$
is a union of at most
![]() $12k$
elements of
$12k$
elements of
![]() $\beta _j$
.
$\beta _j$
.
Apply induction to
![]() $G_j$
with
$G_j$
with
![]() $S_i^j$
in place of
$S_i^j$
in place of
![]() $S_i$
and
$S_i$
and
![]() $R_j$
in place of
$R_j$
in place of
![]() $R$
. Thus, there is a graph
$R$
. Thus, there is a graph
![]() $H_j$
of treewidth at most
$H_j$
of treewidth at most
![]() $c$
, a
$c$
, a
![]() $c$
-clique
$c$
-clique
![]() $\{x_1, \dotsc, x_{c - 1}, y\}$
of
$\{x_1, \dotsc, x_{c - 1}, y\}$
of
![]() $H_j$
, and an
$H_j$
, and an
![]() $H_j$
-partition
$H_j$
-partition
![]() $(V^j_x \,:\, x \in V(H_j))$
of
$(V^j_x \,:\, x \in V(H_j))$
of
![]() $G_j$
of width at most
$G_j$
of width at most
![]() $W$
such that
$W$
such that
![]() $V^j_{x_i} = S^j_i \setminus \big(S^j_1 \cup \dotsb \cup S^j_{i - 1}\big)$
for each
$V^j_{x_i} = S^j_i \setminus \big(S^j_1 \cup \dotsb \cup S^j_{i - 1}\big)$
for each
![]() $i$
and
$i$
and
![]() $R_j \setminus \big(S_{1}^j \cup \dotsb \cup S_{c - 1}^j\big) \subseteq V^j_{y}$
with
$R_j \setminus \big(S_{1}^j \cup \dotsb \cup S_{c - 1}^j\big) \subseteq V^j_{y}$
with
![]() $|V_{y}| \leqslant 2 \ell (|R_j| - 2k)$
. We may assume that the intersection of
$|V_{y}| \leqslant 2 \ell (|R_j| - 2k)$
. We may assume that the intersection of
![]() $V(H_1)$
and
$V(H_1)$
and
![]() $V(H_2)$
is equal to the clique
$V(H_2)$
is equal to the clique
![]() $K \,:\!=\, \{x_1, \dotsc, x_{c - 1}, y\}$
. Let
$K \,:\!=\, \{x_1, \dotsc, x_{c - 1}, y\}$
. Let
![]() $H$
be the union of
$H$
be the union of
![]() $H_1$
and
$H_1$
and
![]() $H_2$
and consider the
$H_2$
and consider the
![]() $H$
-partition
$H$
-partition
![]() $(V_x \,:\, x \in V(H))$
of
$(V_x \,:\, x \in V(H))$
of
![]() $G$
given by
$G$
given by
![]() $V_x \,:\!=\, V^j_x$
for
$V_x \,:\!=\, V^j_x$
for
![]() $x \in V(H_j) \setminus V(H_{3-j})$
and
$x \in V(H_j) \setminus V(H_{3-j})$
and
![]() $V_x \,:\!=\, V^1_x \cup V^2_x$
for
$V_x \,:\!=\, V^1_x \cup V^2_x$
for
![]() $x \in K$
. As
$x \in K$
. As
![]() $H_1$
and
$H_1$
and
![]() $H_2$
both have treewidth at most
$H_2$
both have treewidth at most
![]() $c$
, so does
$c$
, so does
![]() $H$
.
$H$
.
Now
![]() $\{x_1, \dotsc, x_{c - 1}, y\}$
is a
$\{x_1, \dotsc, x_{c - 1}, y\}$
is a
![]() $c$
-clique,
$c$
-clique,
![]() $V_{x_i} = S_{i} \setminus (S_1 \cup \dotsb \cup S_{i - 1})$
and
$V_{x_i} = S_{i} \setminus (S_1 \cup \dotsb \cup S_{i - 1})$
and
![]() $R \setminus S \subseteq V_y$
with
$R \setminus S \subseteq V_y$
with
The other parts do not change and so we have the desired
![]() $H$
-partition of
$H$
-partition of
![]() $G$
.
$G$
.
We are now ready to prove Lemma 8.
Proof of Lemma 8. Let
![]() $\beta$
be a
$\beta$
be a
![]() $(c,f)$
-disjointed
$(c,f)$
-disjointed
![]() $\ell$
-covering of
$\ell$
-covering of
![]() $G$
. If
$G$
. If
![]() $|V(G)| \lt 4k$
, then the trivial partition
$|V(G)| \lt 4k$
, then the trivial partition
![]() $\{V(G)\}$
satisfies the claim. Otherwise
$\{V(G)\}$
satisfies the claim. Otherwise
![]() $|V(G)| \geqslant 4k$
. Let
$|V(G)| \geqslant 4k$
. Let
![]() $R \subseteq V(G)$
with
$R \subseteq V(G)$
with
![]() $|R| = 4k$
. Let
$|R| = 4k$
. Let
![]() $S_1,\dots,S_{c-1}$
be arbitrary elements of
$S_1,\dots,S_{c-1}$
be arbitrary elements of
![]() $\beta$
. Since
$\beta$
. Since
![]() $\beta$
is an
$\beta$
is an
![]() $\ell$
-covering,
$\ell$
-covering,
![]() $|S_i| \leqslant \ell \leqslant 12 \ell k$
for each
$|S_i| \leqslant \ell \leqslant 12 \ell k$
for each
![]() $i$
. Now Lemma 8 follows from Lemma 9.
$i$
. Now Lemma 8 follows from Lemma 9.
Lemmas 5 and 8 imply the following result:
Corollary 10.
Let
![]() $k,c,d,\ell \in{\mathbb{N}}$
. For any graph
$k,c,d,\ell \in{\mathbb{N}}$
. For any graph
![]() $G$
, if
$G$
, if
![]() $\textrm{tw}(G)\lt k$
and
$\textrm{tw}(G)\lt k$
and
![]() $G$
has a
$G$
has a
![]() $(c,d)$
-disjointed
$(c,d)$
-disjointed
![]() $\ell$
-covering, then
$\ell$
-covering, then
![]() $G$
has
$G$
has
![]() $c$
-tree-partition-width
$c$
-tree-partition-width
![]() $\textrm{tpw}_c(G) \leqslant 2 c d \ell (12 k)^c$
.
$\textrm{tpw}_c(G) \leqslant 2 c d \ell (12 k)^c$
.
Note that the singleton partition of any graph with maximum degree
![]() $\Delta$
is
$\Delta$
is
![]() $(1,\Delta )$
-disjointed. So Corollary 10 with
$(1,\Delta )$
-disjointed. So Corollary 10 with
![]() $c=\ell =1$
and
$c=\ell =1$
and
![]() $d=\Delta$
implies Lemma 2 (even with the same constant 24). Indeed, the proof of Lemma 8 in the case of graphs with bounded degree is equivalent to the proof of Lemma 2.
$d=\Delta$
implies Lemma 2 (even with the same constant 24). Indeed, the proof of Lemma 8 in the case of graphs with bounded degree is equivalent to the proof of Lemma 2.
To conclude this section, Lemmas 6 and 8 imply the following characterisation of underlying treewidth.
Theorem 11.
The underlying treewidth of a graph class
![]() $\mathcal{G}$
equals the minimum
$\mathcal{G}$
equals the minimum
![]() $c \in{\mathbb{N}}_0$
such that, for some function
$c \in{\mathbb{N}}_0$
such that, for some function
![]() $g \,:\,{\mathbb{N}} \to{\mathbb{N}}$
, every graph
$g \,:\,{\mathbb{N}} \to{\mathbb{N}}$
, every graph
![]() $G \in \mathcal{G}$
has a
$G \in \mathcal{G}$
has a
![]() $(c,g(\textrm{tw}(G)))$
-disjointed
$(c,g(\textrm{tw}(G)))$
-disjointed
![]() $g(\textrm{tw}(G))$
-partition.
$g(\textrm{tw}(G))$
-partition.
4. Lower bounds
We now define two graphs that provide lower bounds on the underlying treewidth of various graph classes. Recall that
![]() $\widehat{\ell G}$
is the graph obtained from
$\widehat{\ell G}$
is the graph obtained from
![]() $\ell$
disjoint copies of a graph
$\ell$
disjoint copies of a graph
![]() $G$
by adding one dominant vertex. For
$G$
by adding one dominant vertex. For
![]() $c,\ell \in{\mathbb{N}}$
, define graphs
$c,\ell \in{\mathbb{N}}$
, define graphs
![]() $G_{c, \ell }$
and
$G_{c, \ell }$
and
![]() $C_{c, \ell }$
recursively as follows. First,
$C_{c, \ell }$
recursively as follows. First,
![]() $G_{1, \ell } \,:\!=\, P_{\ell + 1}$
is the path on
$G_{1, \ell } \,:\!=\, P_{\ell + 1}$
is the path on
![]() $\ell + 1$
vertices, and
$\ell + 1$
vertices, and
![]() $C_{1, \ell } \,:\!=\, K_{1, \ell }$
is the star with
$C_{1, \ell } \,:\!=\, K_{1, \ell }$
is the star with
![]() $\ell$
leaves. Further, for
$\ell$
leaves. Further, for
![]() $c \geqslant 2$
, let
$c \geqslant 2$
, let
![]() $G_{c, \ell } \,:\!=\, \widehat{\ell \, G_{c - 1, \ell }}$
and
$G_{c, \ell } \,:\!=\, \widehat{\ell \, G_{c - 1, \ell }}$
and
![]() $C_{c, \ell } \,:\!=\, \widehat{\ell \, C_{c - 1, \ell }}$
. Note that
$C_{c, \ell } \,:\!=\, \widehat{\ell \, C_{c - 1, \ell }}$
. Note that
![]() $C_{c, \ell }$
is the closure of the rooted complete
$C_{c, \ell }$
is the closure of the rooted complete
![]() $\ell$
-ary tree of height
$\ell$
-ary tree of height
![]() $c$
. Here, the closure of rooted tree
$c$
. Here, the closure of rooted tree
![]() $T$
is the graph
$T$
is the graph
![]() $G$
with
$G$
with
![]() $V(G)=V(T)$
and
$V(G)=V(T)$
and
![]() $vw\in E(G)$
whenever
$vw\in E(G)$
whenever
![]() $v$
is an ancestor of
$v$
is an ancestor of
![]() $w$
or
$w$
or
![]() $w$
is an ancestor of
$w$
is an ancestor of
![]() $v$
.
$v$
.
The next lemma collects together some useful and well-known properties of
![]() $G_{c, \ell }$
and
$G_{c, \ell }$
and
![]() $C_{c, \ell }$
.
$C_{c, \ell }$
.
Lemma 12.
For all
![]() $c,\ell \in{\mathbb{N}}$
,
$c,\ell \in{\mathbb{N}}$
,
-
(i)
 $\textrm{tw}(G_{c, \ell }) = \textrm{tw}(C_{c, \ell }) = c$
;
$\textrm{tw}(G_{c, \ell }) = \textrm{tw}(C_{c, \ell }) = c$
; -
(ii) for any
 $\ell$
-partition of
$\ell$
-partition of
 $G \in \{ G_{c, \ell }, C_{c, \ell } \}$
, there is a
$G \in \{ G_{c, \ell }, C_{c, \ell } \}$
, there is a
 $(c + 1)$
-clique in
$(c + 1)$
-clique in
 $G$
whose vertices are in distinct parts;
$G$
whose vertices are in distinct parts;
-
(iii)
 $G_{c, \ell }$
and
$G_{c, \ell }$
and
 $C_{c, \ell }$
both have
$C_{c, \ell }$
both have
 $(c - 1)$
-tree-partition-width greater than
$(c - 1)$
-tree-partition-width greater than
 $\ell$
;
$\ell$
; -
(iv)
 $G_{2, \ell }$
is outerplanar,
$G_{2, \ell }$
is outerplanar,
 $G_{3, \ell }$
is planar,
$G_{3, \ell }$
is planar,
 $G_{4, \ell }$
is linklessly embeddable;
$G_{4, \ell }$
is linklessly embeddable;
-
(v)
 $G_{c, \ell }$
is
$G_{c, \ell }$
is
 $K_{c, \max \{c, 3\}}$
-minor-free;
$K_{c, \max \{c, 3\}}$
-minor-free;
-
(vi)
 $C_{c, \ell }$
does not contain
$C_{c, \ell }$
does not contain
 $P_{4}$
as an induced subgraph;
$P_{4}$
as an induced subgraph;
-
(vii)
 $C_{c,\ell }$
does not contain
$C_{c,\ell }$
does not contain
 $P_{n}$
as a subgraph for
$P_{n}$
as a subgraph for
 $n\geqslant 2^{c+1}$
.
$n\geqslant 2^{c+1}$
.
Proof. Since
![]() $\textrm{tw}(\widehat{\ell \, G}) = \textrm{tw}(G)+1$
for any graph
$\textrm{tw}(\widehat{\ell \, G}) = \textrm{tw}(G)+1$
for any graph
![]() $G$
and
$G$
and
![]() $\ell \in{\mathbb{N}}$
, part (i) follows by induction.
$\ell \in{\mathbb{N}}$
, part (i) follows by induction.
We establish (ii) by induction on
![]() $c$
. In the case
$c$
. In the case
![]() $c = 1$
, every
$c = 1$
, every
![]() $\ell$
-partition of
$\ell$
-partition of
![]() $P_{\ell + 1}$
or
$P_{\ell + 1}$
or
![]() $K_{1, \ell }$
contains an edge whose endpoints are in different parts, and we are done. Now assume the claim for
$K_{1, \ell }$
contains an edge whose endpoints are in different parts, and we are done. Now assume the claim for
![]() $c - 1$
(
$c - 1$
(
![]() $c \geqslant 2$
) and let
$c \geqslant 2$
) and let
![]() $G \in \{ G_{c - 1, \ell }, C_{c - 1, \ell }\}$
. Consider an
$G \in \{ G_{c - 1, \ell }, C_{c - 1, \ell }\}$
. Consider an
![]() $\ell$
-partition of
$\ell$
-partition of
![]() $\widehat{\ell \, G}$
. At most
$\widehat{\ell \, G}$
. At most
![]() $\ell - 1$
copies of
$\ell - 1$
copies of
![]() $G$
contain a vertex in the same part as the dominant vertex
$G$
contain a vertex in the same part as the dominant vertex
![]() $v$
. Thus, some copy
$v$
. Thus, some copy
![]() $G_0$
of
$G_0$
of
![]() $G$
contains no vertices in the same part as
$G$
contains no vertices in the same part as
![]() $v$
. By induction,
$v$
. By induction,
![]() $G_0$
contains a
$G_0$
contains a
![]() $c$
-clique
$c$
-clique
![]() $K$
whose vertices are in distinct parts. Since
$K$
whose vertices are in distinct parts. Since
![]() $v$
is dominant,
$v$
is dominant,
![]() $K \cup \{v\}$
satisfies the induction hypothesis.
$K \cup \{v\}$
satisfies the induction hypothesis.
Let
![]() $G \in \{G_{c, \ell }, C_{c, \ell } \}$
. Consider an
$G \in \{G_{c, \ell }, C_{c, \ell } \}$
. Consider an
![]() $H$
-partition of
$H$
-partition of
![]() $G$
of width at most
$G$
of width at most
![]() $\ell$
. By (ii),
$\ell$
. By (ii),
![]() $G$
contains a
$G$
contains a
![]() $(c+1)$
-clique whose vertices are in distinct parts. So
$(c+1)$
-clique whose vertices are in distinct parts. So
![]() $\omega (H) \geqslant c+1$
, implying
$\omega (H) \geqslant c+1$
, implying
![]() $\textrm{tw}(H) \geqslant c$
. This establishes (iii).
$\textrm{tw}(H) \geqslant c$
. This establishes (iii).
Observe that
![]() $G_{2, \ell }$
is outerplanar (called a fan graph). The disjoint union of outerplanar graphs is outerplanar and the graph obtained from any outerplanar graph by adding a dominant vertex is planar; thus
$G_{2, \ell }$
is outerplanar (called a fan graph). The disjoint union of outerplanar graphs is outerplanar and the graph obtained from any outerplanar graph by adding a dominant vertex is planar; thus
![]() $G_{3, \ell }$
is planar. The disjoint union of planar graphs is planar, and the graph obtained from any planar graph by adding a dominant vertex is linklessly embeddable; thus
$G_{3, \ell }$
is planar. The disjoint union of planar graphs is planar, and the graph obtained from any planar graph by adding a dominant vertex is linklessly embeddable; thus
![]() $G_{4, \ell }$
is linklessly embeddable. This proves (iv).
$G_{4, \ell }$
is linklessly embeddable. This proves (iv).
We next show that
![]() $G_{c, \ell }$
is
$G_{c, \ell }$
is
![]() $K_{c, \max \{c, 3\}}$
-minor-free.
$K_{c, \max \{c, 3\}}$
-minor-free.
![]() $G_{1, \ell }$
is a path and so has no
$G_{1, \ell }$
is a path and so has no
![]() $K_{1, 3}$
-minor.
$K_{1, 3}$
-minor.
![]() $G_{2, \ell }$
is outerplanar and so has no
$G_{2, \ell }$
is outerplanar and so has no
![]() $K_{2, 3}$
-minor. Let
$K_{2, 3}$
-minor. Let
![]() $c \geqslant 3$
and assume the result holds for smaller
$c \geqslant 3$
and assume the result holds for smaller
![]() $c$
. Suppose that
$c$
. Suppose that
![]() $G_{c, \ell }$
contains a
$G_{c, \ell }$
contains a
![]() $K_{c,c}$
-minor. Since
$K_{c,c}$
-minor. Since
![]() $K_{c,c}$
is
$K_{c,c}$
is
![]() $2$
-connected, some copy of
$2$
-connected, some copy of
![]() $G_{c-1, \ell }$
in
$G_{c-1, \ell }$
in
![]() $G_{c, \ell }$
contains a
$G_{c, \ell }$
contains a
![]() $K_{c-1, c}$
-minor. This contradiction establishes (v).
$K_{c-1, c}$
-minor. This contradiction establishes (v).
We show that
![]() $C_{c, \ell }$
contains no induced
$C_{c, \ell }$
contains no induced
![]() $P_{4}$
by induction on
$P_{4}$
by induction on
![]() $c$
. First,
$c$
. First,
![]() $C_{1, \ell } = K_{1, \ell }$
does not contain
$C_{1, \ell } = K_{1, \ell }$
does not contain
![]() $P_{4}$
. Next, suppose that
$P_{4}$
. Next, suppose that
![]() $C_{c-1,\ell }$
does not contain an induced
$C_{c-1,\ell }$
does not contain an induced
![]() $P_{4}$
.
$P_{4}$
.
![]() $P_{4}$
does not have a dominant vertex and so any induced
$P_{4}$
does not have a dominant vertex and so any induced
![]() $P_{4}$
in
$P_{4}$
in
![]() $C_{c, \ell }$
must lie entirely within one copy of
$C_{c, \ell }$
must lie entirely within one copy of
![]() $C_{c-1,\ell }$
. In particular,
$C_{c-1,\ell }$
. In particular,
![]() $C_{c, \ell }$
does not contain an induced
$C_{c, \ell }$
does not contain an induced
![]() $P_{4}$
. This proves (vii).
$P_{4}$
. This proves (vii).
Finally, Nešetřil and Ossona de Mendez [Reference Nešetřil and de Mendez57] proved (vii).
The underlying treewidth of the class of graphs of treewidth at most
![]() $k$
is obviously at most
$k$
is obviously at most
![]() $k$
. Lemma 12 (i) and (iii) imply the following.
$k$
. Lemma 12 (i) and (iii) imply the following.
Corollary 13.
The underlying treewidth of the class of graphs of treewidth at most
![]() $k$
equals
$k$
equals
![]() $k$
.
$k$
.
Corollary 14.
The classes
![]() $\{G_{c,\ell } \,:\, c,\ell \in{\mathbb{N}}\}$
and
$\{G_{c,\ell } \,:\, c,\ell \in{\mathbb{N}}\}$
and
![]() $\{C_{c, \ell } \,:\, c, \ell \in{\mathbb{N}}\}$
both have unbounded underlying treewidth.
$\{C_{c, \ell } \,:\, c, \ell \in{\mathbb{N}}\}$
both have unbounded underlying treewidth.
Proof. Suppose that
![]() $\{G_{c,\ell } \,:\, c,\ell \in{\mathbb{N}}\}$
has underlying treewidth
$\{G_{c,\ell } \,:\, c,\ell \in{\mathbb{N}}\}$
has underlying treewidth
![]() $b$
. Thus, for some function
$b$
. Thus, for some function
![]() $f$
, for all
$f$
, for all
![]() $c, \ell \in{\mathbb{N}}$
, we have
$c, \ell \in{\mathbb{N}}$
, we have
![]() $\textrm{tpw}_b(G_{c, \ell }) \leqslant f(\textrm{tw}(G_{c,\ell })) = f(c)$
. In particular, with
$\textrm{tpw}_b(G_{c, \ell }) \leqslant f(\textrm{tw}(G_{c,\ell })) = f(c)$
. In particular, with
![]() $c \,:\!=\, b + 1$
and
$c \,:\!=\, b + 1$
and
![]() $\ell \,:\!=\, f(c)$
, we have
$\ell \,:\!=\, f(c)$
, we have
![]() $\textrm{tpw}_{c-1}(G_{c,\ell }) \leqslant \ell$
, which contradicts Lemma 12 (iii). The proof for
$\textrm{tpw}_{c-1}(G_{c,\ell }) \leqslant \ell$
, which contradicts Lemma 12 (iii). The proof for
![]() $\{C_{c,\ell } \,:\, c,\ell \in{\mathbb{N}}\}$
is analogous.
$\{C_{c,\ell } \,:\, c,\ell \in{\mathbb{N}}\}$
is analogous.
The graphs
![]() $G_{c, \ell }$
and
$G_{c, \ell }$
and
![]() $C_{c, \ell }$
are common in the graph-theory literature, and are particularly important for clustered colouring [Reference Esperet and Joret35, Reference Kleinberg, Motwani, Raghavan and Venkatasubramanian44, Reference Norin, Scott, Seymour and Wood58, Reference van den Heuvel and Wood75], as we now explain. In an (improperly) vertex-coloured graph, a monochromatic component is a connected component of the subgraph induced by all the vertices of one colour. A graph
$C_{c, \ell }$
are common in the graph-theory literature, and are particularly important for clustered colouring [Reference Esperet and Joret35, Reference Kleinberg, Motwani, Raghavan and Venkatasubramanian44, Reference Norin, Scott, Seymour and Wood58, Reference van den Heuvel and Wood75], as we now explain. In an (improperly) vertex-coloured graph, a monochromatic component is a connected component of the subgraph induced by all the vertices of one colour. A graph
![]() $G$
is
$G$
is
![]() $c$
-colourable with clustering
$c$
-colourable with clustering
![]() $\ell$
if each vertex can be assigned one of
$\ell$
if each vertex can be assigned one of
![]() $c$
colours such that each monochromatic component has at most
$c$
colours such that each monochromatic component has at most
![]() $\ell$
vertices. The clustered chromatic number of a graph class
$\ell$
vertices. The clustered chromatic number of a graph class
![]() $\mathcal{G}$
is the minimum
$\mathcal{G}$
is the minimum
![]() $c \in{\mathbb{N}}$
such that, for some
$c \in{\mathbb{N}}$
such that, for some
![]() $\ell \in{\mathbb{N}}$
, every graph in
$\ell \in{\mathbb{N}}$
, every graph in
![]() $\mathcal{G}$
has a
$\mathcal{G}$
has a
![]() $c$
-colouring with clustering
$c$
-colouring with clustering
![]() $\ell$
. See [Reference Wood79] for a survey on clustered graph colouring. Note that a graph
$\ell$
. See [Reference Wood79] for a survey on clustered graph colouring. Note that a graph
![]() $G$
is
$G$
is
![]() $c$
-colourable with clustering
$c$
-colourable with clustering
![]() $\ell$
if and only if
$\ell$
if and only if
![]() $G$
is contained in
$G$
is contained in
![]() $H \boxtimes K_\ell$
for some graph
$H \boxtimes K_\ell$
for some graph
![]() $H$
with
$H$
with
![]() $\chi (H) \leqslant c$
.
$\chi (H) \leqslant c$
.
Consider a graph class
![]() $\mathcal{G}$
with underlying treewidth
$\mathcal{G}$
with underlying treewidth
![]() $c$
, where every graph in
$c$
, where every graph in
![]() $\mathcal{G}$
has treewidth at most
$\mathcal{G}$
has treewidth at most
![]() $k$
. Thus every graph
$k$
. Thus every graph
![]() $G \in \mathcal{G}$
is contained in
$G \in \mathcal{G}$
is contained in
![]() $H \boxtimes K_\ell$
for some graph
$H \boxtimes K_\ell$
for some graph
![]() $H$
with
$H$
with
![]() $\textrm{tw}(H) \leqslant c$
, where
$\textrm{tw}(H) \leqslant c$
, where
![]() $\ell \,:\!=\, \max \{f(0),\dots,f(k)\}$
and
$\ell \,:\!=\, \max \{f(0),\dots,f(k)\}$
and
![]() $f$
is from the definition of underlying treewidth. Since
$f$
is from the definition of underlying treewidth. Since
![]() $\chi (H) \leqslant \textrm{tw}(H)+1$
for every graph
$\chi (H) \leqslant \textrm{tw}(H)+1$
for every graph
![]() $H$
, it follows that
$H$
, it follows that
![]() $\mathcal{G}$
has clustered chromatic number at most
$\mathcal{G}$
has clustered chromatic number at most
![]() $c+1$
. This means that lower bounds on the clustered chromatic number of a graph class with bounded treewidth provide lower bounds on the underlying treewidth of the class. In particular, it is known that
$c+1$
. This means that lower bounds on the clustered chromatic number of a graph class with bounded treewidth provide lower bounds on the underlying treewidth of the class. In particular, it is known that
![]() $G_{c,\ell }$
and
$G_{c,\ell }$
and
![]() $C_{c,\ell }$
are not
$C_{c,\ell }$
are not
![]() $c$
-colourable with clustering
$c$
-colourable with clustering
![]() $\ell$
(see [Reference Wood79]), which implies Lemma 12 (iii) by the above connection. See [Reference Norin, Scott, Seymour and Wood58] for more examples of graphs
$\ell$
(see [Reference Wood79]), which implies Lemma 12 (iii) by the above connection. See [Reference Norin, Scott, Seymour and Wood58] for more examples of graphs
![]() $G$
that are not
$G$
that are not
![]() $c$
-colourable with clustering
$c$
-colourable with clustering
![]() $\ell$
, implying
$\ell$
, implying
![]() $\textrm{tpw}_{c-1}(G) \gt \ell$
.
$\textrm{tpw}_{c-1}(G) \gt \ell$
.
5. Excluding a minor
This section uses disjointed partitions to determine the underlying treewidth of several minor-closed classes of interest.
The next definition enables
![]() $K_t$
-minor-free graphs and
$K_t$
-minor-free graphs and
![]() $K_{s,t}$
-minor-free graphs to be handled simultaneously. For
$K_{s,t}$
-minor-free graphs to be handled simultaneously. For
![]() $s,t\in{\mathbb{N}}$
, let
$s,t\in{\mathbb{N}}$
, let
![]() $\mathcal{K}_{s,t}$
be the class of graphs
$\mathcal{K}_{s,t}$
be the class of graphs
![]() $G$
for which there is a partition
$G$
for which there is a partition
![]() $\{A,B\}$
of
$\{A,B\}$
of
![]() $V(G)$
such that
$V(G)$
such that
![]() $|A| = s$
and
$|A| = s$
and
![]() $|B| = t$
;
$|B| = t$
;
![]() $vw \in E(G)$
for all
$vw \in E(G)$
for all
![]() $v \in A$
and
$v \in A$
and
![]() $w \in B$
; and
$w \in B$
; and
![]() $G[B]$
is connected. Obviously, every graph in
$G[B]$
is connected. Obviously, every graph in
![]() $\mathcal{K}_{s,t}$
contains
$\mathcal{K}_{s,t}$
contains
![]() $K_{s,t}$
. Similarly, we obtain
$K_{s,t}$
. Similarly, we obtain
![]() $K_t$
as a minor of any
$K_t$
as a minor of any
![]() $G \in \mathcal{K}_{t-2,t}$
by contracting a matching between
$G \in \mathcal{K}_{t-2,t}$
by contracting a matching between
![]() $A$
and
$A$
and
![]() $B$
of size
$B$
of size
![]() $t-2$
whose end-vertices are distinct from the end-vertices of some edge of
$t-2$
whose end-vertices are distinct from the end-vertices of some edge of
![]() $G[B]$
.
$G[B]$
.
Lemma 15.
Let
![]() $G$
be a graph with no minor in
$G$
be a graph with no minor in
![]() $\mathcal{K}_{s,t}$
. Assume
$\mathcal{K}_{s,t}$
. Assume
![]() $\{A,B\}$
is a partition of
$\{A,B\}$
is a partition of
![]() $V(G)$
such that
$V(G)$
such that
![]() $G[B]$
is connected and every vertex in
$G[B]$
is connected and every vertex in
![]() $B$
has at least
$B$
has at least
![]() $s$
neighbours in
$s$
neighbours in
![]() $A$
. Then
$A$
. Then
![]() $|B| \leqslant \delta |A|$
for some
$|B| \leqslant \delta |A|$
for some
![]() $\delta = \delta (s,t)$
.
$\delta = \delta (s,t)$
.
Proof. The following proof technique is well-known [Reference Liu and Wood53, Reference de Mendez, Oum and Wood59]. Assign vertices in
![]() $B$
to pairs of vertices in
$B$
to pairs of vertices in
![]() $A$
as follows. Initially, no vertices in
$A$
as follows. Initially, no vertices in
![]() $B$
are assigned. If there is an unassigned vertex
$B$
are assigned. If there is an unassigned vertex
![]() $v \in B$
adjacent to distinct vertices
$v \in B$
adjacent to distinct vertices
![]() $x,y \in A$
and no vertex in
$x,y \in A$
and no vertex in
![]() $B$
is already assigned to
$B$
is already assigned to
![]() $\{x, y\}$
, then assign
$\{x, y\}$
, then assign
![]() $v$
to
$v$
to
![]() $\{x,y\}$
. Repeat this operation until no more vertices in
$\{x,y\}$
. Repeat this operation until no more vertices in
![]() $B$
can be assigned. Let
$B$
can be assigned. Let
![]() $B_1$
and
$B_1$
and
![]() $B_2$
be the sets of assigned and unassigned vertices in
$B_2$
be the sets of assigned and unassigned vertices in
![]() $B$
, respectively. Let
$B$
, respectively. Let
![]() $G^{\prime}$
be the graph obtained from
$G^{\prime}$
be the graph obtained from
![]() $G[A\cup B_1]$
by contracting
$G[A\cup B_1]$
by contracting
![]() $vx$
into
$vx$
into
![]() $x$
, for each vertex
$x$
, for each vertex
![]() $v \in B_1$
assigned to
$v \in B_1$
assigned to
![]() $\{x, y\}$
. Thus
$\{x, y\}$
. Thus
![]() $G^{\prime}$
is a minor of
$G^{\prime}$
is a minor of
![]() $G$
with
$G$
with
![]() $V(G^{\prime}) = A$
and
$V(G^{\prime}) = A$
and
![]() $|E(G^{\prime})| \geqslant |B_1|$
. For each vertex
$|E(G^{\prime})| \geqslant |B_1|$
. For each vertex
![]() $v \in B_2$
, the set
$v \in B_2$
, the set
![]() $N_G(v) \cap A$
is a clique in
$N_G(v) \cap A$
is a clique in
![]() $G^{\prime}$
(otherwise
$G^{\prime}$
(otherwise
![]() $v$
would have been assigned to a pair of non-adjacent neighbours) of size at least
$v$
would have been assigned to a pair of non-adjacent neighbours) of size at least
![]() $s$
. For each
$s$
. For each
![]() $s$
-clique
$s$
-clique
![]() $C$
in
$C$
in
![]() $G^{\prime}$
, there are at most
$G^{\prime}$
, there are at most
![]() $t-1$
vertices
$t-1$
vertices
![]() $v \in B_2$
with
$v \in B_2$
with
![]() $C \subseteq N_G(v)$
, otherwise
$C \subseteq N_G(v)$
, otherwise
![]() $G$
has a minor in
$G$
has a minor in
![]() $\mathcal{K}_{s,t}$
(since
$\mathcal{K}_{s,t}$
(since
![]() $G[B]$
is connected). Since
$G[B]$
is connected). Since
![]() $G^{\prime}$
has no minor in
$G^{\prime}$
has no minor in
![]() $\mathcal{K}_{s,t}$
, we have
$\mathcal{K}_{s,t}$
, we have
![]() $|E(G^{\prime})| \leqslant \delta |A|$
for some
$|E(G^{\prime})| \leqslant \delta |A|$
for some
![]() $\delta = \delta (s,t)$
; see [Reference Kostochka45–Reference Kühn and Osthus50, Reference Reed and Wood61, Reference Thomason71, Reference Thomason72] for explicit bounds on
$\delta = \delta (s,t)$
; see [Reference Kostochka45–Reference Kühn and Osthus50, Reference Reed and Wood61, Reference Thomason71, Reference Thomason72] for explicit bounds on
![]() $\delta$
. Thus
$\delta$
. Thus
![]() $|B_1| \leqslant \delta |A|$
. Moreover,
$|B_1| \leqslant \delta |A|$
. Moreover,
![]() $G^{\prime}$
is
$G^{\prime}$
is
![]() $2 \delta$
-degenerate. Every
$2 \delta$
-degenerate. Every
![]() $d$
-degenerate graph on
$d$
-degenerate graph on
![]() $n$
vertices has at most
$n$
vertices has at most
![]() $\binom{d}{s - 1} n$
cliques of order
$\binom{d}{s - 1} n$
cliques of order
![]() $s$
[Reference Wood78, Lemma 18]. Thus
$s$
[Reference Wood78, Lemma 18]. Thus
![]() $|B_2| \leqslant (t - 1)\binom{2\delta }{s - 1}|A|$
. Hence
$|B_2| \leqslant (t - 1)\binom{2\delta }{s - 1}|A|$
. Hence
![]() $|B| = |B_1| + |B_2| \leqslant \big(\delta + (t - 1) \binom{2\delta }{s - 1}\big)|A|$
.
$|B| = |B_1| + |B_2| \leqslant \big(\delta + (t - 1) \binom{2\delta }{s - 1}\big)|A|$
.
The following Erdős–Pósa type result is useful for showing disjointedness. It follows from well-known results in the literature; see [Reference Campbell12] for details.
Lemma 16.
Let
![]() $\mathcal{H}$
be a set of connected subgraphs of a graph
$\mathcal{H}$
be a set of connected subgraphs of a graph
![]() $G$
. Then, for every non-negative integer
$G$
. Then, for every non-negative integer
![]() $\ell$
, either there are
$\ell$
, either there are
![]() $\ell + 1$
vertex-disjoint graphs in
$\ell + 1$
vertex-disjoint graphs in
![]() $\mathcal{H}$
or there is a set
$\mathcal{H}$
or there is a set
![]() $Q \subseteq V(G)$
of size at most
$Q \subseteq V(G)$
of size at most
![]() $\ell (\textrm{tw}(G) + 1)$
such that
$\ell (\textrm{tw}(G) + 1)$
such that
![]() $G - Q$
contains no graph of
$G - Q$
contains no graph of
![]() $\mathcal{H}$
.
$\mathcal{H}$
.
Lemma 17.
For fixed
![]() $s,t \in{\mathbb{N}}$
, every graph
$s,t \in{\mathbb{N}}$
, every graph
![]() $G$
with no minor in
$G$
with no minor in
![]() $\mathcal{K}_{s,t}$
and of treewidth
$\mathcal{K}_{s,t}$
and of treewidth
![]() $k$
has
$k$
has
![]() $s$
-tree-partition-width
$s$
-tree-partition-width
![]() $O(k^2)$
.
$O(k^2)$
.
Proof. By Lemma 8 it suffices to show that the singleton partition of
![]() $G$
is
$G$
is
![]() $(s,f)$
-disjointed, where
$(s,f)$
-disjointed, where
![]() $f(n) \,:\!=\, \delta sn (k + 1)$
and
$f(n) \,:\!=\, \delta sn (k + 1)$
and
![]() $\delta \,:\!=\, \delta (s,t)$
from Lemma 15. Let
$\delta \,:\!=\, \delta (s,t)$
from Lemma 15. Let
![]() $S_1,\dots,S_s$
be subsets of
$S_1,\dots,S_s$
be subsets of
![]() $V(G)$
of size at most
$V(G)$
of size at most
![]() $n$
, let
$n$
, let
![]() $S \,:\!=\, S_1 \cup \dots \cup S_s$
, and for each
$S \,:\!=\, S_1 \cup \dots \cup S_s$
, and for each
![]() $i \in \{1,\dots, s\}$
let
$i \in \{1,\dots, s\}$
let
![]() $S^{\prime}_i \,:\!=\, S_i \setminus (S_1 \cup \dots \cup S_{i-1})$
. Let
$S^{\prime}_i \,:\!=\, S_i \setminus (S_1 \cup \dots \cup S_{i-1})$
. Let
![]() $X$
be a connected component of
$X$
be a connected component of
![]() $G-S$
. Let
$G-S$
. Let
![]() $\mathcal{H}$
be the set of connected subgraphs
$\mathcal{H}$
be the set of connected subgraphs
![]() $H$
of
$H$
of
![]() $X$
such that
$X$
such that
![]() $H \cap N\big(S^{\prime}_i\big) \neq \varnothing$
for each
$H \cap N\big(S^{\prime}_i\big) \neq \varnothing$
for each
![]() $i \in \{1,\dots,s\}$
. Say
$i \in \{1,\dots,s\}$
. Say
![]() $\mathcal{R}$
is a maximum-sized set of pairwise disjoint subgraphs in
$\mathcal{R}$
is a maximum-sized set of pairwise disjoint subgraphs in
![]() $\mathcal{H}$
. We may assume that
$\mathcal{H}$
. We may assume that
![]() $\bigcup \{ V(R) \,:\, R \in{\mathcal{R}} \} = V(X)$
. Let
$\bigcup \{ V(R) \,:\, R \in{\mathcal{R}} \} = V(X)$
. Let
![]() $X^{\prime}$
be the graph obtained from
$X^{\prime}$
be the graph obtained from
![]() $G[S \cup V(X)]$
by contracting each subgraph
$G[S \cup V(X)]$
by contracting each subgraph
![]() $R \in{\mathcal{R}}$
into a vertex
$R \in{\mathcal{R}}$
into a vertex
![]() $v_R$
. So
$v_R$
. So
![]() $V(X^{\prime}) = S\cup \{v_R \,:\, R\in{\mathcal{R}}\}$
. Since
$V(X^{\prime}) = S\cup \{v_R \,:\, R\in{\mathcal{R}}\}$
. Since
![]() $X$
is connected,
$X$
is connected,
![]() $\{v_R \,:\, R \in{\mathcal{R}}\}$
induces a connected subgraph of
$\{v_R \,:\, R \in{\mathcal{R}}\}$
induces a connected subgraph of
![]() $X^{\prime}$
. By construction, in
$X^{\prime}$
. By construction, in
![]() $X^{\prime}$
, each vertex
$X^{\prime}$
, each vertex
![]() $v_R$
has at least
$v_R$
has at least
![]() $s$
neighbours in
$s$
neighbours in
![]() $S$
. By Lemma 15,
$S$
. By Lemma 15,
![]() $|{\mathcal{R}}| \leqslant \delta |S|$
. By Lemma 16, there is a set
$|{\mathcal{R}}| \leqslant \delta |S|$
. By Lemma 16, there is a set
![]() $Q \subseteq V(X)$
of size at most
$Q \subseteq V(X)$
of size at most
![]() $\delta |S| (k + 1) \leqslant f(n)$
such that
$\delta |S| (k + 1) \leqslant f(n)$
such that
![]() $X-Q$
contains no graph in
$X-Q$
contains no graph in
![]() $\mathcal{H}$
. Thus each component
$\mathcal{H}$
. Thus each component
![]() $Y$
of
$Y$
of
![]() $X-Q$
satisfies
$X-Q$
satisfies
![]() $V(Y) \cap N_G\big(S^{\prime}_i\big) = \varnothing$
for some
$V(Y) \cap N_G\big(S^{\prime}_i\big) = \varnothing$
for some
![]() $i \in \{1,\dots,s\}$
. Hence, the singleton partition of
$i \in \{1,\dots,s\}$
. Hence, the singleton partition of
![]() $G$
is
$G$
is
![]() $(s, f)$
-disjointed.
$(s, f)$
-disjointed.
We now determine the underlying treewidth of
![]() $K_t$
- and
$K_t$
- and
![]() $K_{s,t}$
-minor-free graphs.
$K_{s,t}$
-minor-free graphs.
Theorem 18.
For fixed
![]() $t\in{\mathbb{N}}$
with
$t\in{\mathbb{N}}$
with
![]() $t\geqslant 2$
, the underlying treewidth of the class of
$t\geqslant 2$
, the underlying treewidth of the class of
![]() $K_t$
-minor-free graphs equals
$K_t$
-minor-free graphs equals
![]() $t-2$
. In particular, every
$t-2$
. In particular, every
![]() $K_t$
-minor-free graph of treewidth
$K_t$
-minor-free graph of treewidth
![]() $k$
has
$k$
has
![]() $(t-2)$
-tree-partition-width
$(t-2)$
-tree-partition-width
![]() $O(k^2)$
.
$O(k^2)$
.
Proof. Since
![]() $K_t$
is a minor of every graph in
$K_t$
is a minor of every graph in
![]() $\mathcal{K}_{t-2,t}$
, Lemma 17 implies that every
$\mathcal{K}_{t-2,t}$
, Lemma 17 implies that every
![]() $K_t$
-minor-free graph of treewidth
$K_t$
-minor-free graph of treewidth
![]() $k$
has
$k$
has
![]() $(t-2)$
-tree-partition-width
$(t-2)$
-tree-partition-width
![]() $O(k^2)$
. Thus the underlying treewidth of the class of
$O(k^2)$
. Thus the underlying treewidth of the class of
![]() $K_t$
-minor-free graphs is at most
$K_t$
-minor-free graphs is at most
![]() $t-2$
. Suppose for contradiction that equality does not hold. That is, for some function
$t-2$
. Suppose for contradiction that equality does not hold. That is, for some function
![]() $f$
, every
$f$
, every
![]() $K_t$
-minor-free graph
$K_t$
-minor-free graph
![]() $G$
has
$G$
has
![]() $(t-3)$
-tree-partition-width at most
$(t-3)$
-tree-partition-width at most
![]() $f(\textrm{tw}(G))$
. Let
$f(\textrm{tw}(G))$
. Let
![]() $\ell \,:\!=\, f(t-2)$
. The graph
$\ell \,:\!=\, f(t-2)$
. The graph
![]() $G_{t - 2, \ell }$
in Lemma 12 has treewidth
$G_{t - 2, \ell }$
in Lemma 12 has treewidth
![]() $t-2$
and is thus
$t-2$
and is thus
![]() $K_t$
-minor-free. However, by Lemma 12,
$K_t$
-minor-free. However, by Lemma 12,
![]() $\textrm{tpw}_{t-3}(G_{t - 2, \ell })\gt \ell = f(t - 2) = f(\textrm{tw}(G_{t - 2, \ell }))$
, which is the required contradiction.
$\textrm{tpw}_{t-3}(G_{t - 2, \ell })\gt \ell = f(t - 2) = f(\textrm{tw}(G_{t - 2, \ell }))$
, which is the required contradiction.
Theorem 19.
For fixed
![]() $s,t \in{\mathbb{N}}$
with
$s,t \in{\mathbb{N}}$
with
![]() $t \geqslant \max \{s,3\}$
, the underlying treewidth of the class of
$t \geqslant \max \{s,3\}$
, the underlying treewidth of the class of
![]() $K_{s,t}$
-minor-free graphs equals
$K_{s,t}$
-minor-free graphs equals
![]() $s$
. In particular, every
$s$
. In particular, every
![]() $K_{s,t}$
-minor-free graph
$K_{s,t}$
-minor-free graph
![]() $G$
of treewidth
$G$
of treewidth
![]() $k$
has
$k$
has
![]() $s$
-tree-partition-width
$s$
-tree-partition-width
![]() $O(k^2)$
.
$O(k^2)$
.
Proof. Since
![]() $K_{s,t}$
is a subgraph of every graph in
$K_{s,t}$
is a subgraph of every graph in
![]() $\mathcal{K}_{s,t}$
, Lemma 17 implies that every
$\mathcal{K}_{s,t}$
, Lemma 17 implies that every
![]() $K_{s,t}$
-minor-free graph
$K_{s,t}$
-minor-free graph
![]() $G$
of treewidth
$G$
of treewidth
![]() $k$
has
$k$
has
![]() $s$
-tree-partition-width
$s$
-tree-partition-width
![]() $O(k^2)$
. Thus the underlying treewidth of the class of
$O(k^2)$
. Thus the underlying treewidth of the class of
![]() $K_{s,t}$
-minor-free graphs is at most
$K_{s,t}$
-minor-free graphs is at most
![]() $s$
. Suppose that it is at most
$s$
. Suppose that it is at most
![]() $s - 1$
. Thus for some function
$s - 1$
. Thus for some function
![]() $f$
, every
$f$
, every
![]() $K_{s,t}$
-minor-free graph
$K_{s,t}$
-minor-free graph
![]() $G$
satisfies
$G$
satisfies
![]() $\textrm{tpw}_{s-1}(G) \leqslant f(\textrm{tw}(G))$
. Let
$\textrm{tpw}_{s-1}(G) \leqslant f(\textrm{tw}(G))$
. Let
![]() $\ell \,:\!=\, f(s)$
. The graph
$\ell \,:\!=\, f(s)$
. The graph
![]() $G_{s,\ell }$
given by Lemma 12 has treewidth
$G_{s,\ell }$
given by Lemma 12 has treewidth
![]() $s$
and is
$s$
and is
![]() $K_{s,\max \{s,3\}}$
-minor-free, implying it is
$K_{s,\max \{s,3\}}$
-minor-free, implying it is
![]() $K_{s,t}$
-minor-free (since
$K_{s,t}$
-minor-free (since
![]() $t \geqslant \max \{s,3\}$
). However, by Lemma 12,
$t \geqslant \max \{s,3\}$
). However, by Lemma 12,
![]() $\textrm{tpw}_{s - 1}(G_{s, \ell }) \gt \ell = f(s) = f(\textrm{tw}(G_{s, \ell }))$
, which is the required contradiction.
$\textrm{tpw}_{s - 1}(G_{s, \ell }) \gt \ell = f(s) = f(\textrm{tw}(G_{s, \ell }))$
, which is the required contradiction.
For
![]() $t \leqslant 2$
, Theorem 19 is improved as follows:
$t \leqslant 2$
, Theorem 19 is improved as follows:
Proposition 20.
For
![]() $s,t \in{\mathbb{N}}$
with
$s,t \in{\mathbb{N}}$
with
![]() $s \leqslant t \leqslant 2$
, the underlying treewidth of the class of
$s \leqslant t \leqslant 2$
, the underlying treewidth of the class of
![]() $K_{s,t}$
-minor-free graphs equals
$K_{s,t}$
-minor-free graphs equals
![]() $s-1$
.
$s-1$
.
Proof. Every
![]() $K_{1,1}$
-minor-free graph
$K_{1,1}$
-minor-free graph
![]() $G$
has no edges, and so
$G$
has no edges, and so
![]() $\textrm{tpw}_0(G) \leqslant 1$
. Every
$\textrm{tpw}_0(G) \leqslant 1$
. Every
![]() $K_{1,2}$
-minor-free graph
$K_{1,2}$
-minor-free graph
![]() $G$
has at most one edge in each component, and so
$G$
has at most one edge in each component, and so
![]() $\textrm{tpw}_0(G) \leqslant 2$
. Each block of any
$\textrm{tpw}_0(G) \leqslant 2$
. Each block of any
![]() $K_{2,2}$
-minor-free graph
$K_{2,2}$
-minor-free graph
![]() $G$
is a triangle, an edge or an isolated vertex; so
$G$
is a triangle, an edge or an isolated vertex; so
![]() $\textrm{tpw}_1(G) \leqslant 2$
.
$\textrm{tpw}_1(G) \leqslant 2$
.
Since planar graphs are
![]() $K_5$
- and
$K_5$
- and
![]() $K_{3,3}$
-minor-free, Theorem 18 or Theorem 19 imply the next result (where the lower bound holds since the graph
$K_{3,3}$
-minor-free, Theorem 18 or Theorem 19 imply the next result (where the lower bound holds since the graph
![]() $G_{3,\ell }$
in Lemma 12 is planar).
$G_{3,\ell }$
in Lemma 12 is planar).
Theorem 21.
The underlying treewidth of the class of planar graphs equals
![]() $3$
. In particular, every planar graph of treewidth
$3$
. In particular, every planar graph of treewidth
![]() $k$
has
$k$
has
![]() $3$
-tree-partition-width
$3$
-tree-partition-width
![]() $O(k^2)$
.
$O(k^2)$
.
It follows from Euler’s formula that every graph with Euler genus at most
![]() $g$
is
$g$
is
![]() $K_{3, 2g + 3}$
-minor-free. Thus Lemma 12 and Theorem 19 imply the following.
$K_{3, 2g + 3}$
-minor-free. Thus Lemma 12 and Theorem 19 imply the following.
Theorem 22.
The underlying treewidth of the class of graphs embeddable on any fixed surface
![]() $\Sigma$
equals
$\Sigma$
equals
![]() $3$
. In particular, every graph embeddable in
$3$
. In particular, every graph embeddable in
![]() $\Sigma$
and of treewidth
$\Sigma$
and of treewidth
![]() $k$
has
$k$
has
![]() $3$
-tree-partition-width
$3$
-tree-partition-width
![]() $O(k^2)$
.
$O(k^2)$
.
Since every linklessly embeddable graph is
![]() $K_6$
-minor-free and
$K_6$
-minor-free and
![]() $K_{4,4}$
-minor-free [Reference Robertson, Seymour and Thomas67], Theorem 18 or Theorem 19 imply the next result, where the lower bound follows from Lemma 12.
$K_{4,4}$
-minor-free [Reference Robertson, Seymour and Thomas67], Theorem 18 or Theorem 19 imply the next result, where the lower bound follows from Lemma 12.
Theorem 23.
The underlying treewidth of the class of linklessly embeddable graphs equals
![]() $4$
. In particular, every linklessly embeddable graph of treewidth
$4$
. In particular, every linklessly embeddable graph of treewidth
![]() $k$
has
$k$
has
![]() $4$
-tree-partition-width
$4$
-tree-partition-width
![]() $O(k^2)$
.
$O(k^2)$
.
It is an open problem to determine the underlying treewidth of a given minor-closed class
![]() $\mathcal{G}$
. It is possible that the clustered chromatic number of
$\mathcal{G}$
. It is possible that the clustered chromatic number of
![]() $\mathcal{G}$
equals the underlying treewidth of
$\mathcal{G}$
equals the underlying treewidth of
![]() $\mathcal{G}$
plus
$\mathcal{G}$
plus
![]() $1$
. This is true for any minor-closed class with underlying treewidth at most
$1$
. This is true for any minor-closed class with underlying treewidth at most
![]() $1$
by results of Norin, Scott, Seymour, and Wood [Reference Norin, Scott, Seymour and Wood58] and Ding and Oporowski [Reference Ding and Oporowski20]; see [Reference Campbell12]. See [Reference Norin, Scott, Seymour and Wood58] for a conjectured value of the clustered chromatic number of
$1$
by results of Norin, Scott, Seymour, and Wood [Reference Norin, Scott, Seymour and Wood58] and Ding and Oporowski [Reference Ding and Oporowski20]; see [Reference Campbell12]. See [Reference Norin, Scott, Seymour and Wood58] for a conjectured value of the clustered chromatic number of
![]() $\mathcal{G}$
. It follows from a result of DeVos, Ding, Oporowski, Sanders, Reed, Seymour, and Vertigan [Reference DeVos, Ding, Oporowski, Sanders, Reed, Seymour and Vertigan15] that every minor-closed graph class
$\mathcal{G}$
. It follows from a result of DeVos, Ding, Oporowski, Sanders, Reed, Seymour, and Vertigan [Reference DeVos, Ding, Oporowski, Sanders, Reed, Seymour and Vertigan15] that every minor-closed graph class
![]() $\mathcal{G}$
with underlying treewidth
$\mathcal{G}$
with underlying treewidth
![]() $c$
has clustered chromatic number at most
$c$
has clustered chromatic number at most
![]() $2(c+1)$
; see [Reference Campbell12].
$2(c+1)$
; see [Reference Campbell12].
6. Excluding a topological minor
This section studies the underlying treewidth of graphs classes defined by an excluded topological minor. We conclude that a monotone graph class has bounded underlying treewidth if and only if it excludes some fixed topological minor.
Theorem 24.
For every fixed multigraph
![]() $X$
with
$X$
with
![]() $p$
vertices, every
$p$
vertices, every
![]() $X$
-topological minor-free graph
$X$
-topological minor-free graph
![]() $G$
of treewidth
$G$
of treewidth
![]() $k$
has
$k$
has
![]() $p$
-tree-partition-width
$p$
-tree-partition-width
![]() $O(k^2)$
.
$O(k^2)$
.
Proof. By Lemma 8 it suffices to show that the singleton partition of
![]() $G$
is
$G$
is
![]() $(p,f)$
-disjointed, where
$(p,f)$
-disjointed, where
![]() $f(n) \in O(kn)$
. To this end, let
$f(n) \in O(kn)$
. To this end, let
![]() $S_1,\dots,S_p$
be subsets of
$S_1,\dots,S_p$
be subsets of
![]() $V(G)$
of size at most
$V(G)$
of size at most
![]() $n$
, let
$n$
, let
![]() $S \,:\!=\, S_1 \cup \dots \cup S_p$
, and for each
$S \,:\!=\, S_1 \cup \dots \cup S_p$
, and for each
![]() $i \in \{1, \dots, p\}$
let
$i \in \{1, \dots, p\}$
let
![]() $S^{\prime}_i \,:\!=\, S_i \setminus (S_1 \cup \dots \cup S_{i-1})$
. We may assume that
$S^{\prime}_i \,:\!=\, S_i \setminus (S_1 \cup \dots \cup S_{i-1})$
. We may assume that
![]() $V(X) = \{1,\dots,p\}$
. Let
$V(X) = \{1,\dots,p\}$
. Let
![]() $\mathcal{H}$
be the set of connected subgraphs
$\mathcal{H}$
be the set of connected subgraphs
![]() $H$
of
$H$
of
![]() $G-S$
such that
$G-S$
such that
![]() $V(H) \cap N_G\big(S^{\prime}_i\big) \neq \varnothing$
for each
$V(H) \cap N_G\big(S^{\prime}_i\big) \neq \varnothing$
for each
![]() $i \in \{1,\dots,p\}$
.
$i \in \{1,\dots,p\}$
.
Consider any set
![]() $\mathcal{J}$
of pairwise vertex-disjoint graphs in
$\mathcal{J}$
of pairwise vertex-disjoint graphs in
![]() $\mathcal{H}$
of maximum size. Assign subgraphs in
$\mathcal{H}$
of maximum size. Assign subgraphs in
![]() $\mathcal{J}$
to pairs of vertices in
$\mathcal{J}$
to pairs of vertices in
![]() $S$
as follows. Initially, no subgraphs in
$S$
as follows. Initially, no subgraphs in
![]() $\mathcal{J}$
are assigned. If there is an unassigned subgraph
$\mathcal{J}$
are assigned. If there is an unassigned subgraph
![]() $H \in \mathcal{J}$
adjacent to vertices
$H \in \mathcal{J}$
adjacent to vertices
![]() $x \in S^{\prime}_i$
and
$x \in S^{\prime}_i$
and
![]() $y \in S^{\prime}_j$
, for some distinct
$y \in S^{\prime}_j$
, for some distinct
![]() $i,j \in \{1,\dots,p\}$
, and no subgraph in
$i,j \in \{1,\dots,p\}$
, and no subgraph in
![]() $\mathcal{J}$
is already assigned to
$\mathcal{J}$
is already assigned to
![]() $\{x,y\}$
, then assign
$\{x,y\}$
, then assign
![]() $H$
to
$H$
to
![]() $\{x,y\}$
. Repeat this operation until no more subgraphs in
$\{x,y\}$
. Repeat this operation until no more subgraphs in
![]() $\mathcal{J}$
can be assigned.
$\mathcal{J}$
can be assigned.
Let
![]() $\mathcal{J}_1$
and
$\mathcal{J}_1$
and
![]() $\mathcal{J}_2$
be the sets of assigned and unassigned subgraphs in
$\mathcal{J}_2$
be the sets of assigned and unassigned subgraphs in
![]() $\mathcal{J}$
respectively. Let
$\mathcal{J}$
respectively. Let
![]() $G^{\prime}$
be the graph obtained from
$G^{\prime}$
be the graph obtained from
![]() $G$
as follows: for each
$G$
as follows: for each
![]() $H \in \mathcal{J}_1$
assigned to
$H \in \mathcal{J}_1$
assigned to
![]() $\{x,y\}$
, contract an
$\{x,y\}$
, contract an
![]() $(x,y)$
-path through
$(x,y)$
-path through
![]() $H$
down to a single edge
$H$
down to a single edge
![]() $xy$
. Delete any remaining vertices not in
$xy$
. Delete any remaining vertices not in
![]() $S$
. Thus
$S$
. Thus
![]() $G^{\prime}$
is a topological minor of
$G^{\prime}$
is a topological minor of
![]() $G$
with
$G$
with
![]() $V(G^{\prime}) = S$
and
$V(G^{\prime}) = S$
and
![]() ${|E(G^{\prime})| \geqslant |\mathcal{J}_1}|$
. Consider a subgraph
${|E(G^{\prime})| \geqslant |\mathcal{J}_1}|$
. Consider a subgraph
![]() $H \in \mathcal{J}_2$
. Since
$H \in \mathcal{J}_2$
. Since
![]() $H \in{\mathcal{H}}$
there are neighbours
$H \in{\mathcal{H}}$
there are neighbours
![]() $v_1,\dots,v_p$
of
$v_1,\dots,v_p$
of
![]() $H$
with
$H$
with
![]() $v_i \in S^{\prime}_i$
for each
$v_i \in S^{\prime}_i$
for each
![]() $i \in \{1,\dots,p\}$
. Since
$i \in \{1,\dots,p\}$
. Since
![]() $H \in \mathcal{J}_2$
, the set
$H \in \mathcal{J}_2$
, the set
![]() $\{v_1,\dots,v_p\}$
is a clique in
$\{v_1,\dots,v_p\}$
is a clique in
![]() $G^{\prime}$
(otherwise
$G^{\prime}$
(otherwise
![]() $H$
could have been assigned to some non-adjacent
$H$
could have been assigned to some non-adjacent
![]() $v_i$
and
$v_i$
and
![]() $v_j$
). Charge
$v_j$
). Charge
![]() $H$
to
$H$
to
![]() $(v_1,\dots,v_p)$
.
$(v_1,\dots,v_p)$
.
Suppose that there is a set
![]() $\mathcal{J}^{\prime}$
of at least
$\mathcal{J}^{\prime}$
of at least
![]() $|E(X)|$
subgraphs in
$|E(X)|$
subgraphs in
![]() $\mathcal{J}_2$
charged to some clique
$\mathcal{J}_2$
charged to some clique
![]() $(v_1,\dots,v_p)$
in
$(v_1,\dots,v_p)$
in
![]() $G^{\prime}$
with
$G^{\prime}$
with
![]() $v_i \in S^{\prime}_i$
. Label
$v_i \in S^{\prime}_i$
. Label
![]() $\mathcal{J}^{\prime} = \{H_e \,:\, e \in E(X)\}$
. For
$\mathcal{J}^{\prime} = \{H_e \,:\, e \in E(X)\}$
. For
![]() $e = ij \in E(X)$
, let
$e = ij \in E(X)$
, let
![]() $P_e$
be a
$P_e$
be a
![]() $(v_i,v_j)$
-path through
$(v_i,v_j)$
-path through
![]() $H_e$
. Thus
$H_e$
. Thus
![]() $\{v_i P_e v_j \,:\, e = ij \in E(X)\}$
defines an
$\{v_i P_e v_j \,:\, e = ij \in E(X)\}$
defines an
![]() $X$
-topological minor in
$X$
-topological minor in
![]() $G$
with branch vertices
$G$
with branch vertices
![]() $v_1, \dotsc, v_p$
. This contradiction shows that there are fewer than
$v_1, \dotsc, v_p$
. This contradiction shows that there are fewer than
![]() $|E(X)|$
subgraphs in
$|E(X)|$
subgraphs in
![]() $\mathcal{J}_2$
charged to each clique
$\mathcal{J}_2$
charged to each clique
![]() $(v_1, \dotsc, v_p)$
in
$(v_1, \dotsc, v_p)$
in
![]() $G^{\prime}$
with
$G^{\prime}$
with
![]() $v_i \in S^{\prime}_i$
.
$v_i \in S^{\prime}_i$
.
Since
![]() $G^{\prime}$
is
$G^{\prime}$
is
![]() $X$
-topological-minor-free,
$X$
-topological-minor-free,
![]() $|E(G^{\prime})| \leqslant \gamma |S|$
for some
$|E(G^{\prime})| \leqslant \gamma |S|$
for some
![]() $\gamma = \gamma (X)$
; see [Reference Bollobás and Thomason10, Reference Thomas and Wollan70] for explicit bounds on
$\gamma = \gamma (X)$
; see [Reference Bollobás and Thomason10, Reference Thomas and Wollan70] for explicit bounds on
![]() $\gamma$
. Thus
$\gamma$
. Thus
![]() $|\mathcal{J}_1| \leqslant \gamma |S|$
. Moreover,
$|\mathcal{J}_1| \leqslant \gamma |S|$
. Moreover,
![]() $G^{\prime}$
is
$G^{\prime}$
is
![]() $2\gamma$
-degenerate. Every
$2\gamma$
-degenerate. Every
![]() $d$
-degenerate graph on
$d$
-degenerate graph on
![]() $n$
vertices has at most
$n$
vertices has at most
![]() $\binom{d}{p-1}n$
cliques of order
$\binom{d}{p-1}n$
cliques of order
![]() $p$
[Reference Wood78, Lemma 18]. Thus
$p$
[Reference Wood78, Lemma 18]. Thus
![]() $|\mathcal{J}_2| \lt |E(X)| \binom{2\gamma }{p-1}|S|$
. Hence
$|\mathcal{J}_2| \lt |E(X)| \binom{2\gamma }{p-1}|S|$
. Hence
![]() $|\mathcal{J}| = |\mathcal{J}_1| + |\mathcal{J}_2| \lt (\gamma + |E(X)| \binom{2\gamma }{p-1}) |S|$
. Define
$|\mathcal{J}| = |\mathcal{J}_1| + |\mathcal{J}_2| \lt (\gamma + |E(X)| \binom{2\gamma }{p-1}) |S|$
. Define
Since
![]() $|S| \leqslant pn$
, by Lemma 16, there is a set
$|S| \leqslant pn$
, by Lemma 16, there is a set
![]() $Q \subseteq V(G-S)$
of size at most
$Q \subseteq V(G-S)$
of size at most
![]() $f(n)$
such that no subgraph of
$f(n)$
such that no subgraph of
![]() $G-(S\cup Q)$
is in
$G-(S\cup Q)$
is in
![]() $\mathcal{H}$
. So every component
$\mathcal{H}$
. So every component
![]() $Y$
of
$Y$
of
![]() $G-(S\cup Q)$
satisfies
$G-(S\cup Q)$
satisfies
![]() $Y \cap N_{G}\big(S^{\prime}_i\big) = \varnothing$
for some
$Y \cap N_{G}\big(S^{\prime}_i\big) = \varnothing$
for some
![]() $i \in \{1, \dots, p\}$
. Hence the singleton partition of
$i \in \{1, \dots, p\}$
. Hence the singleton partition of
![]() $G$
is
$G$
is
![]() $(p,f)$
-disjointed.
$(p,f)$
-disjointed.
Theorem 25.
The underlying treewidth of the class of
![]() $K_t$
-topological-minor-free graphs equals
$K_t$
-topological-minor-free graphs equals
![]() $t-2$
if
$t-2$
if
![]() $t \in \{2,3,4\}$
and equals
$t \in \{2,3,4\}$
and equals
![]() $t$
if
$t$
if
![]() $t \geqslant 5$
.
$t \geqslant 5$
.
Proof. For
![]() $t \in \{2,3,4\}$
, a graph is
$t \in \{2,3,4\}$
, a graph is
![]() $K_t$
-topological-minor-free if and only if it has treewidth at most
$K_t$
-topological-minor-free if and only if it has treewidth at most
![]() $t-2$
. So the result follows from Corollary 13. Now assume that
$t-2$
. So the result follows from Corollary 13. Now assume that
![]() $t \geqslant 5$
.
$t \geqslant 5$
.
Theorem 24 implies that the underlying treewidth of the class of
![]() $K_t$
-topological-minor-free graphs is at most
$K_t$
-topological-minor-free graphs is at most
![]() $t$
. Suppose for the sake of contradiction that it is at most
$t$
. Suppose for the sake of contradiction that it is at most
![]() $t-1$
. That is, there is a function
$t-1$
. That is, there is a function
![]() $f$
such that every
$f$
such that every
![]() $K_t$
-topological-minor-free graph
$K_t$
-topological-minor-free graph
![]() $G$
has
$G$
has
![]() $(t-1)$
-tree-partition-width at most
$(t-1)$
-tree-partition-width at most
![]() $f(\textrm{tw}(G))$
. Let
$f(\textrm{tw}(G))$
. Let
![]() $\ell \,:\!=\, f(t)$
. Let
$\ell \,:\!=\, f(t)$
. Let
![]() $G_1$
be the graph
$G_1$
be the graph
![]() $G_{t-2,\ell }$
from Lemma 12. So
$G_{t-2,\ell }$
from Lemma 12. So
![]() $\textrm{tw}(G_1) = t-2$
, implying
$\textrm{tw}(G_1) = t-2$
, implying
![]() $G_1$
is
$G_1$
is
![]() $K_t$
-topological-minor-free, and for every
$K_t$
-topological-minor-free, and for every
![]() $H$
-partition of
$H$
-partition of
![]() $G_{1}$
with width
$G_{1}$
with width
![]() $\ell$
, there is a
$\ell$
, there is a
![]() $(t - 1)$
-clique in
$(t - 1)$
-clique in
![]() $G_1$
whose vertices are in distinct parts.
$G_1$
whose vertices are in distinct parts.
Let
![]() $n \gg t,\ell$
be a sufficiently large integer as detailed below. Let
$n \gg t,\ell$
be a sufficiently large integer as detailed below. Let
![]() $G_2$
be the graph with vertex-set
$G_2$
be the graph with vertex-set
![]() $\{v_1,\dots,v_{t-1}\}\cup \{x_1,\dots,x_{n}\}$
where
$\{v_1,\dots,v_{t-1}\}\cup \{x_1,\dots,x_{n}\}$
where
![]() $\{v_1,\dots,v_{t-1}\}$
is a clique,
$\{v_1,\dots,v_{t-1}\}$
is a clique,
![]() $x_1, \dots, x_{n}$
is a path, and
$x_1, \dots, x_{n}$
is a path, and
![]() $v_i x_j$
is an edge whenever
$v_i x_j$
is an edge whenever
![]() $j = a(t-1)+i$
for some
$j = a(t-1)+i$
for some
![]() $a \in{\mathbb{N}}_0$
. Each subpath
$a \in{\mathbb{N}}_0$
. Each subpath
![]() $x_{a(t-1)+1},\dots,x_{a(t-1)+(t-1)}$
is called a clump. By construction, each vertex
$x_{a(t-1)+1},\dots,x_{a(t-1)+(t-1)}$
is called a clump. By construction, each vertex
![]() $v_i$
has one neighbour in every clump. Since each vertex
$v_i$
has one neighbour in every clump. Since each vertex
![]() $x_j$
has degree at most
$x_j$
has degree at most
![]() $3$
, the graph
$3$
, the graph
![]() $G_2$
has exactly
$G_2$
has exactly
![]() $t-1$
vertices of degree at least
$t-1$
vertices of degree at least
![]() $4$
. Thus
$4$
. Thus
![]() $G_2$
contains no
$G_2$
contains no
![]() $K_t$
-topological minor (since
$K_t$
-topological minor (since
![]() $t \geqslant 5$
). Let
$t \geqslant 5$
). Let
![]() $X_j \,:\!=\, \{v_1,\dots,v_{t-1},x_j,x_{j+1}\}$
. Then
$X_j \,:\!=\, \{v_1,\dots,v_{t-1},x_j,x_{j+1}\}$
. Then
![]() $(X_1,X_2,\dots,X_{n-1})$
is a path-decomposition of
$(X_1,X_2,\dots,X_{n-1})$
is a path-decomposition of
![]() $G_2$
with width
$G_2$
with width
![]() $t$
; thus
$t$
; thus
![]() $\textrm{tw}(G_2) \leqslant t$
.
$\textrm{tw}(G_2) \leqslant t$
.
Let
![]() $G$
be obtained by pasting a copy of
$G$
be obtained by pasting a copy of
![]() $G_2$
onto each
$G_2$
onto each
![]() $(t-1)$
-clique
$(t-1)$
-clique
![]() $C$
of
$C$
of
![]() $G_1$
, where the vertices
$G_1$
, where the vertices
![]() $v_1,\dots,v_{t-1}$
in
$v_1,\dots,v_{t-1}$
in
![]() $G_2$
are identified with
$G_2$
are identified with
![]() $C$
. Since each of
$C$
. Since each of
![]() $G_1$
and
$G_1$
and
![]() $G_2$
have treewidth at most
$G_2$
have treewidth at most
![]() $t$
, so too does
$t$
, so too does
![]() $G$
. Since each of
$G$
. Since each of
![]() $G_1$
and
$G_1$
and
![]() $G_2$
contain no
$G_2$
contain no
![]() $K_t$
-topological-minor,
$K_t$
-topological-minor,
![]() $G$
contains no
$G$
contains no
![]() $K_t$
-topological minor. Thus
$K_t$
-topological minor. Thus
![]() $G$
has a
$G$
has a
![]() $(t-1)$
-tree-partition
$(t-1)$
-tree-partition
![]() $\mathcal{P} = (V_h \,:\, h \in V(H))$
of width
$\mathcal{P} = (V_h \,:\, h \in V(H))$
of width
![]() $\ell$
.
$\ell$
.
Since
![]() $G_1$
is a subgraph of
$G_1$
is a subgraph of
![]() $G$
, there is a
$G$
, there is a
![]() $(t-1)$
-clique
$(t-1)$
-clique
![]() $C$
in
$C$
in
![]() $G_1$
whose vertices are in distinct parts of
$G_1$
whose vertices are in distinct parts of
![]() $\mathcal{P}$
. Let
$\mathcal{P}$
. Let
![]() $C^{\prime}$
be the set of parts in
$C^{\prime}$
be the set of parts in
![]() $\mathcal{P}$
intersecting
$\mathcal{P}$
intersecting
![]() $C$
. Thus
$C$
. Thus
![]() $|C^{\prime}| = |C| = t-1$
. Let
$|C^{\prime}| = |C| = t-1$
. Let
![]() $P_0$
be the path in the copy of
$P_0$
be the path in the copy of
![]() $G_2$
pasted onto
$G_2$
pasted onto
![]() $C$
in
$C$
in
![]() $G$
. At most
$G$
. At most
![]() $(t-1)(\ell -1)$
of the vertices in
$(t-1)(\ell -1)$
of the vertices in
![]() $P_0$
are in the parts of
$P_0$
are in the parts of
![]() $\mathcal{P}$
in
$\mathcal{P}$
in
![]() $C^{\prime}$
. Thus, for
$C^{\prime}$
. Thus, for
![]() $n \gg t, \ell$
, there is a subpath
$n \gg t, \ell$
, there is a subpath
![]() $P_1$
of
$P_1$
of
![]() $P_0$
that contains at least
$P_0$
that contains at least
![]() $(t-1)\ell +2$
clumps, and no vertex of
$(t-1)\ell +2$
clumps, and no vertex of
![]() $P_1$
is in the parts of
$P_1$
is in the parts of
![]() $\mathcal{P}$
in
$\mathcal{P}$
in
![]() $C^{\prime}$
. Let
$C^{\prime}$
. Let
![]() $A$
be the first clump in
$A$
be the first clump in
![]() $P_1$
. Let
$P_1$
. Let
![]() $A^{\prime}$
be the parts of
$A^{\prime}$
be the parts of
![]() $\mathcal{P}$
that intersect
$\mathcal{P}$
that intersect
![]() $A$
. Since
$A$
. Since
![]() $G[A]$
is connected,
$G[A]$
is connected,
![]() $H[A^{\prime}]$
is connected. Since
$H[A^{\prime}]$
is connected. Since
![]() $|A^{\prime}| \leqslant |A| = t-1$
, there are at most
$|A^{\prime}| \leqslant |A| = t-1$
, there are at most
![]() $(t-1)\ell$
vertices in the parts in
$(t-1)\ell$
vertices in the parts in
![]() $A^{\prime}$
. Thus at most
$A^{\prime}$
. Thus at most
![]() $(t-1)\ell$
clumps in
$(t-1)\ell$
clumps in
![]() $P_1$
intersect parts in
$P_1$
intersect parts in
![]() $A^{\prime}$
. Hence
$A^{\prime}$
. Hence
![]() $P_1$
contains a clump
$P_1$
contains a clump
![]() $B$
that intersects no part in
$B$
that intersects no part in
![]() $A^{\prime}$
. Let
$A^{\prime}$
. Let
![]() $B^{\prime}$
be the parts in
$B^{\prime}$
be the parts in
![]() $\mathcal{P}$
that intersect
$\mathcal{P}$
that intersect
![]() $B$
. Thus
$B$
. Thus
![]() $A^{\prime} \cap B^{\prime} = \varnothing$
. Since
$A^{\prime} \cap B^{\prime} = \varnothing$
. Since
![]() $G[B]$
is connected,
$G[B]$
is connected,
![]() $H[B^{\prime}]$
is connected. Since
$H[B^{\prime}]$
is connected. Since
![]() $P_1$
is connected and no vertex of
$P_1$
is connected and no vertex of
![]() $P_1$
is in a part in
$P_1$
is in a part in
![]() $C^{\prime}$
, there is a path
$C^{\prime}$
, there is a path
![]() $Q$
in
$Q$
in
![]() $H-C^{\prime}$
from
$H-C^{\prime}$
from
![]() $A^{\prime}$
to
$A^{\prime}$
to
![]() $B^{\prime}$
, with no internal vertex of
$B^{\prime}$
, with no internal vertex of
![]() $Q$
in
$Q$
in
![]() $A^{\prime}\cup B^{\prime}$
. Let
$A^{\prime}\cup B^{\prime}$
. Let
![]() $H^{\prime}$
be obtained from
$H^{\prime}$
be obtained from
![]() $H$
by contracting
$H$
by contracting
![]() $H[A^{\prime}]$
to a vertex
$H[A^{\prime}]$
to a vertex
![]() $a$
, contracting
$a$
, contracting
![]() $H[B^{\prime}]$
to a vertex
$H[B^{\prime}]$
to a vertex
![]() $b$
, and contracting
$b$
, and contracting
![]() $Q$
down to an edge
$Q$
down to an edge
![]() $ab$
. Each vertex in
$ab$
. Each vertex in
![]() $C^{\prime}$
has a neighbour in
$C^{\prime}$
has a neighbour in
![]() $A$
and in
$A$
and in
![]() $B$
. Thus
$B$
. Thus
![]() $C^{\prime}\cup \{a,b\}$
is a
$C^{\prime}\cup \{a,b\}$
is a
![]() $(t+1)$
-clique in
$(t+1)$
-clique in
![]() $H^{\prime}$
. Thus
$H^{\prime}$
. Thus
![]() $H$
contains
$H$
contains
![]() $K_{t+1}$
as a minor, contradicting that
$K_{t+1}$
as a minor, contradicting that
![]() $\textrm{tw}(H) \leqslant t-1$
. Therefore the underlying treewidth of the class of
$\textrm{tw}(H) \leqslant t-1$
. Therefore the underlying treewidth of the class of
![]() $K_t$
-topological-minor-free graphs equals
$K_t$
-topological-minor-free graphs equals
![]() $t$
.
$t$
.
The proof of Theorem 19 is easily adapted to show that for
![]() $s \leqslant 3$
and fixed
$s \leqslant 3$
and fixed
![]() $t$
, every
$t$
, every
![]() $K_{s,t}$
-topological-minor-free graph
$K_{s,t}$
-topological-minor-free graph
![]() $G$
of treewidth
$G$
of treewidth
![]() $k$
has
$k$
has
![]() $s$
-tree-partition-width
$s$
-tree-partition-width
![]() $O(k^2)$
; see [Reference Campbell12]. So the underlying treewidth of the class of
$O(k^2)$
; see [Reference Campbell12]. So the underlying treewidth of the class of
![]() $K_{s,t}$
-topological minor-free graphs equals
$K_{s,t}$
-topological minor-free graphs equals
![]() $s$
if
$s$
if
![]() $s \leqslant 3$
and
$s \leqslant 3$
and
![]() $t \geqslant \max \{s,3\}$
. But the proof does not generalise for
$t \geqslant \max \{s,3\}$
. But the proof does not generalise for
![]() $s \geqslant 4$
. Determining the underlying treewidth of the class of
$s \geqslant 4$
. Determining the underlying treewidth of the class of
![]() $K_{s,t}$
-topological-minor-free graphs is an interesting open problem. Also, in the
$K_{s,t}$
-topological-minor-free graphs is an interesting open problem. Also, in the
![]() $s = 2$
case we can use Menger’s Theorem instead of Lemma 16 to show that every
$s = 2$
case we can use Menger’s Theorem instead of Lemma 16 to show that every
![]() $K_{2,t}$
-topological-minor-free graph of treewidth
$K_{2,t}$
-topological-minor-free graph of treewidth
![]() $k$
has
$k$
has
![]() $2$
-tree-partition-width
$2$
-tree-partition-width
![]() $O(t^2k)$
; see [Reference Campbell12]. A result of Leaf and Seymour [Reference Leaf and Seymour52, (4.4)] implies that every
$O(t^2k)$
; see [Reference Campbell12]. A result of Leaf and Seymour [Reference Leaf and Seymour52, (4.4)] implies that every
![]() $K_{2,t}$
-minor-free graph has treewidth at most
$K_{2,t}$
-minor-free graph has treewidth at most
![]() $3t/2$
. Thus every
$3t/2$
. Thus every
![]() $K_{2,t}$
-minor-free graph has
$K_{2,t}$
-minor-free graph has
![]() $2$
-tree-partition-width
$2$
-tree-partition-width
![]() $O(t^3)$
. It is open whether every
$O(t^3)$
. It is open whether every
![]() $K_{2,t}$
-minor-free graph has
$K_{2,t}$
-minor-free graph has
![]() $2$
-tree-partition-width
$2$
-tree-partition-width
![]() $O(t)$
, which would be best possible by Observation 1. It is easily seen that every
$O(t)$
, which would be best possible by Observation 1. It is easily seen that every
![]() $K_{1,t}$
-minor-free graph has tree-partition-width
$K_{1,t}$
-minor-free graph has tree-partition-width
![]() $O(t)$
; see [Reference Campbell12].
$O(t)$
; see [Reference Campbell12].
We now show that
![]() $c$
-tree-partition-width is well-behaved under subdivisions (for
$c$
-tree-partition-width is well-behaved under subdivisions (for
![]() $c \geqslant 1$
).
$c \geqslant 1$
).
Lemma 26.
For
![]() $c,t \in{\mathbb{N}}$
, if
$c,t \in{\mathbb{N}}$
, if
![]() $\tilde{G}$
is a subdivision of a graph
$\tilde{G}$
is a subdivision of a graph
![]() $G$
with
$G$
with
![]() $\textrm{tpw}_c(G)\leqslant t$
, then
$\textrm{tpw}_c(G)\leqslant t$
, then
![]() $\textrm{tpw}_c(\tilde{G}) \leqslant t^2+t$
if
$\textrm{tpw}_c(\tilde{G}) \leqslant t^2+t$
if
![]() $c = 1$
and
$c = 1$
and
![]() $\textrm{tpw}_c(\tilde{G}) \leqslant t$
if
$\textrm{tpw}_c(\tilde{G}) \leqslant t$
if
![]() $c \geqslant 2$
.
$c \geqslant 2$
.
Proof. We first prove the
![]() $c = 1$
case. If
$c = 1$
case. If
![]() $t = 1$
, then
$t = 1$
, then
![]() $G$
is a forest. So
$G$
is a forest. So
![]() $\tilde{G}$
is a forest and the claim follows. Now assume
$\tilde{G}$
is a forest and the claim follows. Now assume
![]() $t \geqslant 2$
. Let
$t \geqslant 2$
. Let
![]() $(V_x \,:\, x \in V(T))$
be a tree-partition of
$(V_x \,:\, x \in V(T))$
be a tree-partition of
![]() $G$
with width at most
$G$
with width at most
![]() $t$
. We construct a tree
$t$
. We construct a tree
![]() $T^{\prime}$
from
$T^{\prime}$
from
![]() $T$
and a
$T$
and a
![]() $T^{\prime}$
-partition of
$T^{\prime}$
-partition of
![]() $\tilde{G}$
iteratively as follows. Orient the edges of
$\tilde{G}$
iteratively as follows. Orient the edges of
![]() $T$
so that each vertex has in-degree at most
$T$
so that each vertex has in-degree at most
![]() $1$
. Say an edge
$1$
. Say an edge
![]() $vw$
of
$vw$
of
![]() $G$
is replaced by the
$G$
is replaced by the
![]() $(v,w)$
-path
$(v,w)$
-path
![]() $v_0,v_1,\dots,v_s,v_{s+1}$
in
$v_0,v_1,\dots,v_s,v_{s+1}$
in
![]() $\tilde{G}$
. If
$\tilde{G}$
. If
![]() $v$
and
$v$
and
![]() $w$
are in the same part
$w$
are in the same part
![]() $V_x$
(where
$V_x$
(where
![]() $x \in V(H)$
), then add a path of bags
$x \in V(H)$
), then add a path of bags
![]() $V_x,\{v_1,v_{s}\},\{v_2,v_{s-1}\},\ldots$
to
$V_x,\{v_1,v_{s}\},\{v_2,v_{s-1}\},\ldots$
to
![]() $T^{\prime}$
. If
$T^{\prime}$
. If
![]() $v \in V_x$
and
$v \in V_x$
and
![]() $w \in V_y$
then
$w \in V_y$
then
![]() $xy \in E(T)$
. Assume
$xy \in E(T)$
. Assume
![]() $xy$
is directed from
$xy$
is directed from
![]() $x$
to
$x$
to
![]() $y$
. Add
$y$
. Add
![]() $v_1$
to
$v_1$
to
![]() $V_y$
and add a path of bags
$V_y$
and add a path of bags
![]() $V_y,\{v_2,v_{s}\},\{v_3,v_{s-2}\},\ldots$
to
$V_y,\{v_2,v_{s}\},\{v_3,v_{s-2}\},\ldots$
to
![]() $T^{\prime}$
. Since
$T^{\prime}$
. Since
![]() $|\{uw\in E(G) \,:\, u \in V_x, w \in V_y\}| \leqslant t^2$
, we have
$|\{uw\in E(G) \,:\, u \in V_x, w \in V_y\}| \leqslant t^2$
, we have
![]() $|V_x|\leqslant t^2+t$
for all
$|V_x|\leqslant t^2+t$
for all
![]() $x \in V(T^{\prime})$
. This defines a tree-partition of
$x \in V(T^{\prime})$
. This defines a tree-partition of
![]() $\tilde{G}$
with width at most
$\tilde{G}$
with width at most
![]() $t^2+t$
.
$t^2+t$
.
Now consider the
![]() $c \geqslant 2$
case. If
$c \geqslant 2$
case. If
![]() $t = 1$
, then
$t = 1$
, then
![]() $\textrm{tw}(G) \leqslant c$
. Since subdividing edges does not increase treewidth,
$\textrm{tw}(G) \leqslant c$
. Since subdividing edges does not increase treewidth,
![]() $\textrm{tw}(\tilde{G}) \leqslant c$
, and the claim follows. Now assume
$\textrm{tw}(\tilde{G}) \leqslant c$
, and the claim follows. Now assume
![]() $t \geqslant 2$
. Let
$t \geqslant 2$
. Let
![]() $(V_x \,:\, x\in V(H))$
be an
$(V_x \,:\, x\in V(H))$
be an
![]() $H$
-partition of
$H$
-partition of
![]() $G$
with width at most
$G$
with width at most
![]() $t$
where
$t$
where
![]() $\textrm{tw}(H) \leqslant c$
. We construct a graph
$\textrm{tw}(H) \leqslant c$
. We construct a graph
![]() $H^{\prime}$
of treewidth at most
$H^{\prime}$
of treewidth at most
![]() $c$
from
$c$
from
![]() $H$
and a
$H$
and a
![]() $H^{\prime}$
-partition of
$H^{\prime}$
-partition of
![]() $\tilde{G}$
iteratively as follows. Say an edge
$\tilde{G}$
iteratively as follows. Say an edge
![]() $vw$
of
$vw$
of
![]() $G$
is replaced by the
$G$
is replaced by the
![]() $(v,w)$
-path
$(v,w)$
-path
![]() $v_0,v_1,\dots,v_s,v_{s+1}$
in
$v_0,v_1,\dots,v_s,v_{s+1}$
in
![]() $\tilde{G}$
. If
$\tilde{G}$
. If
![]() $v$
and
$v$
and
![]() $w$
are in the same part
$w$
are in the same part
![]() $V_x$
(where
$V_x$
(where
![]() $x \in V(H)$
), then add a path of bags
$x \in V(H)$
), then add a path of bags
![]() $V_x,\{v_1,v_{s}\},\{v_2,v_{s-1}\},\dotsc$
to
$V_x,\{v_1,v_{s}\},\{v_2,v_{s-1}\},\dotsc$
to
![]() $H^{\prime}$
. If
$H^{\prime}$
. If
![]() $v \in V_x$
and
$v \in V_x$
and
![]() $w \in V_y$
then
$w \in V_y$
then
![]() $xy \in E(H)$
; add a path of bags
$xy \in E(H)$
; add a path of bags
![]() $\{v_1,v_{s}\},\{v_2,v_{s-1}\},\dotsc$
to
$\{v_1,v_{s}\},\{v_2,v_{s-1}\},\dotsc$
to
![]() $H^{\prime}$
, where
$H^{\prime}$
, where
![]() $\{v_1,v_{s}\}$
is adjacent to
$\{v_1,v_{s}\}$
is adjacent to
![]() $x$
and
$x$
and
![]() $y$
in
$y$
in
![]() $H^{\prime}$
. This defines a
$H^{\prime}$
. This defines a
![]() $c$
-tree-partition of
$c$
-tree-partition of
![]() $\tilde{G}$
with width at most
$\tilde{G}$
with width at most
![]() $t$
, as desired.
$t$
, as desired.
Lemma 27.
For all
![]() $c \in{\mathbb{N}}$
, for every graph
$c \in{\mathbb{N}}$
, for every graph
![]() $G$
and every subdivision
$G$
and every subdivision
![]() $G^{\prime}$
of
$G^{\prime}$
of
![]() $G$
,
$G$
,
Proof. Let
![]() $\ell \,:\!=\, \textrm{tpw}_c(G^{\prime})$
. By Lemma 6,
$\ell \,:\!=\, \textrm{tpw}_c(G^{\prime})$
. By Lemma 6,
![]() $G^{\prime}$
has a
$G^{\prime}$
has a
![]() $(c,c\ell )$
-disjointed
$(c,c\ell )$
-disjointed
![]() $\ell$
-partition
$\ell$
-partition
![]() $\beta ^{\prime}$
. Let
$\beta ^{\prime}$
. Let
![]() $\beta \,:\!=\, \{B^{\prime} \cap V(G) \,:\, B^{\prime} \in \beta ^{\prime}\}$
be the corresponding
$\beta \,:\!=\, \{B^{\prime} \cap V(G) \,:\, B^{\prime} \in \beta ^{\prime}\}$
be the corresponding
![]() $\ell$
-partition of
$\ell$
-partition of
![]() $G$
. We show that
$G$
. We show that
![]() $\beta$
is
$\beta$
is
![]() $(c,2c\ell (c\ell +1))$
-disjointed. The result then follows from Corollary 10 as
$(c,2c\ell (c\ell +1))$
-disjointed. The result then follows from Corollary 10 as
![]() $\textrm{tw}(G^{\prime}) = \textrm{tw}(G)$
.
$\textrm{tw}(G^{\prime}) = \textrm{tw}(G)$
.
Let
![]() $B_1, \dotsc, B_c \in \beta$
be distinct non-empty parts and let
$B_1, \dotsc, B_c \in \beta$
be distinct non-empty parts and let
![]() $B^{\prime}_1, \dotsc, B^{\prime}_c$
be the corresponding parts in
$B^{\prime}_1, \dotsc, B^{\prime}_c$
be the corresponding parts in
![]() $\beta ^{\prime}$
. Let
$\beta ^{\prime}$
. Let
![]() $B \,:\!=\, \bigcup \{B_{i} \,:\, i \in \{1,\dots,c\}\}$
and
$B \,:\!=\, \bigcup \{B_{i} \,:\, i \in \{1,\dots,c\}\}$
and
![]() $B^{\prime} \,:\!=\, \bigcup \{B^{\prime}_{i} \,:\, i \in \{1,\dots,c\}\}$
. Observe that every vertex in
$B^{\prime} \,:\!=\, \bigcup \{B^{\prime}_{i} \,:\, i \in \{1,\dots,c\}\}$
. Observe that every vertex in
![]() $B^{\prime} - B$
is an internal vertex of some subdivided edge in
$B^{\prime} - B$
is an internal vertex of some subdivided edge in
![]() $G$
. Let
$G$
. Let
![]() $\tilde{Q} \subseteq V(G)$
be the set of end-vertices of these subdivided edges, so
$\tilde{Q} \subseteq V(G)$
be the set of end-vertices of these subdivided edges, so
![]() $|\tilde{Q}| \leqslant 2 |B^{\prime} - B| \lt 2c \ell$
.
$|\tilde{Q}| \leqslant 2 |B^{\prime} - B| \lt 2c \ell$
.
Let
![]() $X$
be a component of
$X$
be a component of
![]() $G - B$
and let
$G - B$
and let
![]() $Y^{\prime}_1, \dotsc, Y^{\prime}_m$
be the components of
$Y^{\prime}_1, \dotsc, Y^{\prime}_m$
be the components of
![]() $G^{\prime} - B^{\prime}$
that intersect
$G^{\prime} - B^{\prime}$
that intersect
![]() $X$
. Since
$X$
. Since
![]() $\beta ^{\prime}$
is
$\beta ^{\prime}$
is
![]() $(c, c\ell )$
-disjointed, for each
$(c, c\ell )$
-disjointed, for each
![]() $j$
there is some
$j$
there is some
![]() $Q^{\prime}_j \subseteq V\big(Y^{\prime}_j\big)$
of size at most
$Q^{\prime}_j \subseteq V\big(Y^{\prime}_j\big)$
of size at most
![]() $c\ell$
such that every component of
$c\ell$
such that every component of
![]() $Y^{\prime}_j - Q^{\prime}_j$
is disjoint from some
$Y^{\prime}_j - Q^{\prime}_j$
is disjoint from some
![]() $N_{G^{\prime}}\big(B^{\prime}_i\big)$
. Define
$N_{G^{\prime}}\big(B^{\prime}_i\big)$
. Define
![]() $Q_j$
as follows. For each
$Q_j$
as follows. For each
![]() $w \in Q^{\prime}_j$
either
$w \in Q^{\prime}_j$
either
![]() $w \in V(G)$
or
$w \in V(G)$
or
![]() $w$
is an internal vertex of some subdivided edge
$w$
is an internal vertex of some subdivided edge
![]() $uv$
in
$uv$
in
![]() $G$
. In the first case add
$G$
. In the first case add
![]() $w$
to
$w$
to
![]() $Q_j$
, and in the second case add
$Q_j$
, and in the second case add
![]() $u$
and
$u$
and
![]() $v$
to
$v$
to
![]() $Q_j$
. Thus
$Q_j$
. Thus
![]() $|Q_j|\leqslant 2c\ell$
.
$|Q_j|\leqslant 2c\ell$
.
Let
![]() $Q \,:\!=\, (\bigcup \{Q_j \,:\, j \in \{1,\dots,m\} \} \cup \tilde{Q}) \cap V(X)$
. Then
$Q \,:\!=\, (\bigcup \{Q_j \,:\, j \in \{1,\dots,m\} \} \cup \tilde{Q}) \cap V(X)$
. Then
![]() $|Q| \leqslant 2m c \ell + 2c \ell = 2c \ell (m + 1)$
. Let
$|Q| \leqslant 2m c \ell + 2c \ell = 2c \ell (m + 1)$
. Let
![]() $Z$
be a component of
$Z$
be a component of
![]() $X - Q$
. Consider any path
$X - Q$
. Consider any path
![]() $P$
within
$P$
within
![]() $Z$
: in
$Z$
: in
![]() $G^{\prime}$
this is subdivided to give a path
$G^{\prime}$
this is subdivided to give a path
![]() $P^{\prime}$
. As
$P^{\prime}$
. As
![]() $P$
avoids
$P$
avoids
![]() $\tilde{Q}$
, the path
$\tilde{Q}$
, the path
![]() $P^{\prime}$
avoids
$P^{\prime}$
avoids
![]() $B^{\prime}$
. Hence
$B^{\prime}$
. Hence
![]() $V(Z)$
is contained in some component of
$V(Z)$
is contained in some component of
![]() $G^{\prime} - B^{\prime}$
and so within some
$G^{\prime} - B^{\prime}$
and so within some
![]() $Y^{\prime}_j$
. Further,
$Y^{\prime}_j$
. Further,
![]() $P$
avoids
$P$
avoids
![]() $Q_j$
, so
$Q_j$
, so
![]() $P^{\prime}$
avoids
$P^{\prime}$
avoids
![]() $Q^{\prime}_j$
. Hence
$Q^{\prime}_j$
. Hence
![]() $V(Z)$
is contained in some component
$V(Z)$
is contained in some component
![]() $Z^{\prime}$
of
$Z^{\prime}$
of
![]() $Y^{\prime}_j - Q^{\prime}_j$
. By the definition of
$Y^{\prime}_j - Q^{\prime}_j$
. By the definition of
![]() $Q^{\prime}_j$
, there is some
$Q^{\prime}_j$
, there is some
![]() $i$
with
$i$
with
![]() $N_{G^{\prime}}\big(B^{\prime}_i\big) \cap V(Z^{\prime}) = \varnothing$
.
$N_{G^{\prime}}\big(B^{\prime}_i\big) \cap V(Z^{\prime}) = \varnothing$
.
We claim that
![]() $N_{G}(B_i) \cap V(Z) = \varnothing$
. Indeed suppose
$N_{G}(B_i) \cap V(Z) = \varnothing$
. Indeed suppose
![]() $u \in B_i$
and
$u \in B_i$
and
![]() $v \in V(Z)$
are adjacent and consider the corresponding
$v \in V(Z)$
are adjacent and consider the corresponding
![]() $(u,v)$
-path
$(u,v)$
-path
![]() $P^{\prime}$
in
$P^{\prime}$
in
![]() $G^{\prime}$
. Since
$G^{\prime}$
. Since
![]() $v \not \in \tilde{Q}$
, the path
$v \not \in \tilde{Q}$
, the path
![]() $P^{\prime} - u$
avoids
$P^{\prime} - u$
avoids
![]() $B^{\prime}$
and so is within
$B^{\prime}$
and so is within
![]() $Y^{\prime}_j$
(as
$Y^{\prime}_j$
(as
![]() $v \in V(Z) \subseteq V(Y_j)$
). As
$v \in V(Z) \subseteq V(Y_j)$
). As
![]() $v \not \in Q_j$
, the path
$v \not \in Q_j$
, the path
![]() $P^{\prime} - u$
avoids
$P^{\prime} - u$
avoids
![]() $Q^{\prime}_j$
. Hence
$Q^{\prime}_j$
. Hence
![]() $P^{\prime} - u$
is a connected subgraph of
$P^{\prime} - u$
is a connected subgraph of
![]() $Y_j - Q^{\prime}_j$
so is within
$Y_j - Q^{\prime}_j$
so is within
![]() $Z^{\prime}$
(as
$Z^{\prime}$
(as
![]() $v \in V(Z) \subseteq V(Z^{\prime})$
). But then
$v \in V(Z) \subseteq V(Z^{\prime})$
). But then
![]() $N_{G^{\prime}}(u) \cap V(Z^{\prime}) \neq \varnothing$
, a contradiction. Hence
$N_{G^{\prime}}(u) \cap V(Z^{\prime}) \neq \varnothing$
, a contradiction. Hence
![]() $\beta$
is
$\beta$
is
![]() $(c, 2c \ell (m + 1))$
-disjointed. We are left to show that
$(c, 2c \ell (m + 1))$
-disjointed. We are left to show that
![]() $m \leqslant c \ell$
.
$m \leqslant c \ell$
.
For each
![]() $i \in \{1,\dots,m\}$
, let
$i \in \{1,\dots,m\}$
, let
![]() $v_i \in V(Y^{\prime}_i) \cap V(X)$
. For distinct
$v_i \in V(Y^{\prime}_i) \cap V(X)$
. For distinct
![]() $i,j \in \{1,\dots,m\}$
, let
$i,j \in \{1,\dots,m\}$
, let
![]() $P_{i,j}$
be a
$P_{i,j}$
be a
![]() $(v_i,v_j)$
-path in
$(v_i,v_j)$
-path in
![]() $X$
. Since
$X$
. Since
![]() $Y^{\prime}_i$
and
$Y^{\prime}_i$
and
![]() $Y^{\prime}_j$
are distinct components in
$Y^{\prime}_j$
are distinct components in
![]() $G^{\prime} - B^{\prime}$
, there exist a vertex
$G^{\prime} - B^{\prime}$
, there exist a vertex
![]() $w \in B^{\prime} - B$
that is an internal vertex of a subdivided edge in
$w \in B^{\prime} - B$
that is an internal vertex of a subdivided edge in
![]() $P_{i,j}$
. Therefore,
$P_{i,j}$
. Therefore,
![]() $m - 1 \leqslant |B^{\prime} - B| \lt c \ell$
.
$m - 1 \leqslant |B^{\prime} - B| \lt c \ell$
.
Theorem 28.
A monotone graph class
![]() $\mathcal{G}$
has bounded underlying treewidth if and only if
$\mathcal{G}$
has bounded underlying treewidth if and only if
![]() $\mathcal{G}$
excludes some fixed topological minor.
$\mathcal{G}$
excludes some fixed topological minor.
Proof. (
![]() $\Longleftarrow$
) Say
$\Longleftarrow$
) Say
![]() $\mathcal{G}$
excludes some fixed topological minor
$\mathcal{G}$
excludes some fixed topological minor
![]() $X$
on
$X$
on
![]() $p$
vertices. By Theorem 24, every graph
$p$
vertices. By Theorem 24, every graph
![]() $G \in \mathcal{G}$
has
$G \in \mathcal{G}$
has
![]() $p$
-tree-partition-width at most
$p$
-tree-partition-width at most
![]() $O(\textrm{tw}(G)^2)$
. Thus
$O(\textrm{tw}(G)^2)$
. Thus
![]() $\mathcal{G}$
has underlying treewidth at most
$\mathcal{G}$
has underlying treewidth at most
![]() $p$
.
$p$
.
(
![]() $\Longrightarrow$
) Say
$\Longrightarrow$
) Say
![]() $\mathcal{G}$
has underlying treewidth
$\mathcal{G}$
has underlying treewidth
![]() $c$
. That is, there is a function
$c$
. That is, there is a function
![]() $f$
such that
$f$
such that
![]() $\textrm{tpw}_c(G) \leqslant f(\textrm{tw}(G))$
for every graph
$\textrm{tpw}_c(G) \leqslant f(\textrm{tw}(G))$
for every graph
![]() $G \in \mathcal{G}$
. For any
$G \in \mathcal{G}$
. For any
![]() $n \in{\mathbb{N}}$
, by Lemma 12, there is a graph
$n \in{\mathbb{N}}$
, by Lemma 12, there is a graph
![]() $H$
of treewidth
$H$
of treewidth
![]() $c + 1$
and
$c + 1$
and
![]() $\textrm{tpw}_c(H) \gt n$
. Suppose for the sake of contradiction that some subdivision
$\textrm{tpw}_c(H) \gt n$
. Suppose for the sake of contradiction that some subdivision
![]() $H^{\prime}$
of
$H^{\prime}$
of
![]() $H$
is in
$H$
is in
![]() $\mathcal{G}$
. Thus
$\mathcal{G}$
. Thus
![]() $\textrm{tpw}_c(H^{\prime})\leqslant f( \textrm{tw}(H^{\prime})) = f(\textrm{tw}(H)) = f(c+1)$
. By Lemma 27,
$\textrm{tpw}_c(H^{\prime})\leqslant f( \textrm{tw}(H^{\prime})) = f(\textrm{tw}(H)) = f(c+1)$
. By Lemma 27,
We obtain a contradiction taking
![]() $n \gg f(c+1)$
. Thus no subdivision of
$n \gg f(c+1)$
. Thus no subdivision of
![]() $H$
is in
$H$
is in
![]() $\mathcal{G}$
. Since
$\mathcal{G}$
. Since
![]() $\mathcal{G}$
is monotone,
$\mathcal{G}$
is monotone,
![]() $\mathcal{G}$
excludes
$\mathcal{G}$
excludes
![]() $H$
as a topological minor, as desired.
$H$
as a topological minor, as desired.
7. Excluding a subgraph
For a graph
![]() $H$
, a graph
$H$
, a graph
![]() $G$
is
$G$
is
![]() $H$
-free if
$H$
-free if
![]() $G$
contains no subgraph isomorphic to
$G$
contains no subgraph isomorphic to
![]() $H$
. For a finite set of graphs
$H$
. For a finite set of graphs
![]() $\mathcal{H}$
, we say that
$\mathcal{H}$
, we say that
![]() $G$
is
$G$
is
![]() $\mathcal{H}$
-free if
$\mathcal{H}$
-free if
![]() $G$
is
$G$
is
![]() $H$
-free for all
$H$
-free for all
![]() $H \in \mathcal{H}$
. Let
$H \in \mathcal{H}$
. Let
![]() $\mathcal{G}_H$
be the class of
$\mathcal{G}_H$
be the class of
![]() $H$
-free graphs and let
$H$
-free graphs and let
![]() $\mathcal{G}_{\mathcal{H}}$
be the class of
$\mathcal{G}_{\mathcal{H}}$
be the class of
![]() $\mathcal{H}$
-free graphs. This section characterises when
$\mathcal{H}$
-free graphs. This section characterises when
![]() $\mathcal{G}_{\mathcal{H}}$
has bounded underlying treewidth, and determines the exact underlying treewidth for several natural classes. A spider is a subdivision of a star and a spider-forest is a subdivision of a star-forest. For
$\mathcal{G}_{\mathcal{H}}$
has bounded underlying treewidth, and determines the exact underlying treewidth for several natural classes. A spider is a subdivision of a star and a spider-forest is a subdivision of a star-forest. For
![]() $s,t\in{\mathbb{N}}$
with
$s,t\in{\mathbb{N}}$
with
![]() $s\geqslant 2$
, the
$s\geqslant 2$
, the
![]() $(s,t)$
-spider, denoted
$(s,t)$
-spider, denoted
![]() $S_{s,t}$
, is the
$S_{s,t}$
, is the
![]() $(t-1)$
-subdivision of
$(t-1)$
-subdivision of
![]() $K_{1,s}$
. If
$K_{1,s}$
. If
![]() $v$
is the centre of
$v$
is the centre of
![]() $S_{s,t}$
, then each component of
$S_{s,t}$
, then each component of
![]() $S_{s,t}-v$
is called a leg.
$S_{s,t}-v$
is called a leg.
Theorem 29.
For all
![]() $\ell,n,s,t\in{\mathbb{N}}$
where
$\ell,n,s,t\in{\mathbb{N}}$
where
![]() $n,s\geqslant 3$
and
$n,s\geqslant 3$
and
![]() $\ell \geqslant 2$
, and for every finite set
$\ell \geqslant 2$
, and for every finite set
![]() $\mathcal{H}$
of graphs,
$\mathcal{H}$
of graphs,
-
(a)
 $\mathcal{G}_{{\mathcal{H}}}$
has bounded underlying treewidth if and only if
$\mathcal{G}_{{\mathcal{H}}}$
has bounded underlying treewidth if and only if
 $\mathcal{H}$
contains a spider-forest;
$\mathcal{H}$
contains a spider-forest;
-
(b) the underlying treewidth of
 $\mathcal{G}_{P_n}$
equals
$\mathcal{G}_{P_n}$
equals
 $\lfloor{\log n}\rfloor - 1$
;
$\lfloor{\log n}\rfloor - 1$
; -
(c) the underlying treewidth of
 $\mathcal{G}_{\ell \, P_n}$
equals
$\mathcal{G}_{\ell \, P_n}$
equals
 $\lfloor{\log n}\rfloor$
;
$\lfloor{\log n}\rfloor$
; -
(d) the underlying treewidth of
 $\mathcal{G}_{S_{s,t}}$
equals
$\mathcal{G}_{S_{s,t}}$
equals
 $\lfloor{\log t}\rfloor + 1$
;
$\lfloor{\log t}\rfloor + 1$
; -
(e) the underlying treewidth of
 $\mathcal{G}_{\ell \, S_{s,t}}$
equals
$\mathcal{G}_{\ell \, S_{s,t}}$
equals
 $\lfloor{\log t}\rfloor + 2$
.
$\lfloor{\log t}\rfloor + 2$
.
We prove Theorem 29 through a sequence of lemmas.
Lemma 30.
For every finite set
![]() $\mathcal{H}$
of graphs, if
$\mathcal{H}$
of graphs, if
![]() $\mathcal{G}_{\mathcal{H}}$
has bounded underlying treewidth, then
$\mathcal{G}_{\mathcal{H}}$
has bounded underlying treewidth, then
![]() $\mathcal{H}$
contains a spider-forest.
$\mathcal{H}$
contains a spider-forest.
Proof. For the sake of contradiction, suppose that
![]() $\mathcal{H}$
does not contain a spider-forest. Then each graph
$\mathcal{H}$
does not contain a spider-forest. Then each graph
![]() $H \in \mathcal{H}$
contains a cycle or two vertices with degree at least
$H \in \mathcal{H}$
contains a cycle or two vertices with degree at least
![]() $3$
in the same component of
$3$
in the same component of
![]() $H$
. Let
$H$
. Let
![]() $s_H$
be the minimum of the girth of
$s_H$
be the minimum of the girth of
![]() $H$
and the minimum distance between distinct vertices with degree at least
$H$
and the minimum distance between distinct vertices with degree at least
![]() $3$
in the same component of
$3$
in the same component of
![]() $H$
. Let
$H$
. Let
![]() $s \,:\!=\,\max \{s_H\,:\, H\in{\mathcal{H}}\}$
and let
$s \,:\!=\,\max \{s_H\,:\, H\in{\mathcal{H}}\}$
and let
![]() $\mathcal{G}$
be any graph class with unbounded underlying treewidth (such as that in Corollary 14). Let
$\mathcal{G}$
be any graph class with unbounded underlying treewidth (such as that in Corollary 14). Let
![]() $\mathcal{G}^{\prime}$
be the class of
$\mathcal{G}^{\prime}$
be the class of
![]() $(s+1)$
-subdivisions of graphs in
$(s+1)$
-subdivisions of graphs in
![]() $\mathcal{G}$
. Then
$\mathcal{G}$
. Then
![]() $\mathcal{G}^{\prime}$
is
$\mathcal{G}^{\prime}$
is
![]() $H$
-free for all
$H$
-free for all
![]() $H \in{\mathcal{H}}$
and has unbounded underlying treewidth by Lemma 27, a contradiction.
$H \in{\mathcal{H}}$
and has unbounded underlying treewidth by Lemma 27, a contradiction.
Lemma 30 proves the necessity of (i) in Theorem 29.
We now work towards showing
![]() $\mathcal{G}_H$
has bounded underlying treewidth when
$\mathcal{G}_H$
has bounded underlying treewidth when
![]() $H$
is a spider. For a graph
$H$
is a spider. For a graph
![]() $G$
and
$G$
and
![]() $\lambda \in{\mathbb{N}}$
, let
$\lambda \in{\mathbb{N}}$
, let
![]() $G^{(\lambda )}$
be the graph with
$G^{(\lambda )}$
be the graph with
![]() $V(G^{(\lambda )})=V(G)$
and
$V(G^{(\lambda )})=V(G)$
and
![]() $uv\in E(G^{(\lambda )})$
whenever there are
$uv\in E(G^{(\lambda )})$
whenever there are
![]() $\lambda$
internally disjoint
$\lambda$
internally disjoint
![]() $(u,v)$
-paths in
$(u,v)$
-paths in
![]() $G$
.
$G$
.
Lemma 31.
For all
![]() $k,\lambda \in{\mathbb{N}}$
where
$k,\lambda \in{\mathbb{N}}$
where
![]() $\lambda \geqslant k+1$
, if a graph
$\lambda \geqslant k+1$
, if a graph
![]() $G$
has treewidth at most
$G$
has treewidth at most
![]() $k$
, then
$k$
, then
![]() $\textrm{tw}(G^{(\lambda )})\leqslant k$
.
$\textrm{tw}(G^{(\lambda )})\leqslant k$
.
Proof. Let
![]() $\mathcal{W}\,:\!=\, (W_x \,:\, x\in V(T))$
be a tree-decomposition of
$\mathcal{W}\,:\!=\, (W_x \,:\, x\in V(T))$
be a tree-decomposition of
![]() $G$
with width
$G$
with width
![]() $k$
. We may assume that
$k$
. We may assume that
![]() $W_x\neq W_y$
for each
$W_x\neq W_y$
for each
![]() $xy\in E(T)$
. We claim that
$xy\in E(T)$
. We claim that
![]() $\mathcal{W}$
is also a tree-decomposition of
$\mathcal{W}$
is also a tree-decomposition of
![]() $G^{(\lambda )}$
, for which it suffices to show that for every edge
$G^{(\lambda )}$
, for which it suffices to show that for every edge
![]() $vw$
of
$vw$
of
![]() $G^{(\lambda )}$
,
$G^{(\lambda )}$
,
![]() $v$
and
$v$
and
![]() $w$
are in a common bag of
$w$
are in a common bag of
![]() $\mathcal{W}$
. To this end, suppose that
$\mathcal{W}$
. To this end, suppose that
![]() $vw\in E(G^{(\lambda )})$
but there is no bag of
$vw\in E(G^{(\lambda )})$
but there is no bag of
![]() $\mathcal{W}$
containing both
$\mathcal{W}$
containing both
![]() $v$
and
$v$
and
![]() $w$
. Then there is an edge
$w$
. Then there is an edge
![]() $xy\in E(T)$
separating
$xy\in E(T)$
separating
![]() $\{z\in V(T) \,:\, v\in W_z\}$
and
$\{z\in V(T) \,:\, v\in W_z\}$
and
![]() $\{z\in V(T) \,:\, w\in W_z\}$
, which implies that
$\{z\in V(T) \,:\, w\in W_z\}$
, which implies that
![]() $W_x\cap W_y$
is a set of at most
$W_x\cap W_y$
is a set of at most
![]() $k$
vertices separating
$k$
vertices separating
![]() $v$
and
$v$
and
![]() $w$
in
$w$
in
![]() $G$
. On the other hand, since
$G$
. On the other hand, since
![]() $vw\in E(G^{(\lambda )})$
and
$vw\in E(G^{(\lambda )})$
and
![]() $\lambda \geqslant k+1$
, any vertex-set separating
$\lambda \geqslant k+1$
, any vertex-set separating
![]() $v$
and
$v$
and
![]() $w$
must have at least
$w$
must have at least
![]() $k+1$
vertices, a contradiction.
$k+1$
vertices, a contradiction.
Lemma 32.
For all
![]() $s,t \in{\mathbb{N}}$
and
$s,t \in{\mathbb{N}}$
and
![]() $\lambda \geqslant 1+s+st(2t+1)$
, if a graph
$\lambda \geqslant 1+s+st(2t+1)$
, if a graph
![]() $G$
contains no
$G$
contains no
![]() $S_{s,2t+1}$
subgraph, then
$S_{s,2t+1}$
subgraph, then
![]() $G^{(\lambda )}$
contains no
$G^{(\lambda )}$
contains no
![]() $S_{s,t}$
subgraph.
$S_{s,t}$
subgraph.
Proof. Suppose for contradiction that
![]() $S_{s,t}$
is a subgraph of
$S_{s,t}$
is a subgraph of
![]() $G^{(\lambda )}$
. Since
$G^{(\lambda )}$
. Since
![]() $G$
does not contain
$G$
does not contain
![]() $S_{s,2t+1}$
as a subgraph, there is no set of
$S_{s,2t+1}$
as a subgraph, there is no set of
![]() $s$
internally disjoint paths of length at least
$s$
internally disjoint paths of length at least
![]() $2t+2$
in
$2t+2$
in
![]() $G$
between any pair of vertices. Hence, since
$G$
between any pair of vertices. Hence, since
![]() $\lambda \geqslant 1+s+st(2t+1)$
we may greedily replace each edge
$\lambda \geqslant 1+s+st(2t+1)$
we may greedily replace each edge
![]() $uv$
of
$uv$
of
![]() $S_{s,t}$
with a
$S_{s,t}$
with a
![]() $(u,v)$
-path in
$(u,v)$
-path in
![]() $G$
of length between
$G$
of length between
![]() $2$
and
$2$
and
![]() $2t+1$
such that all these paths are internally vertex disjoint from each other, and each of these paths internally avoids
$2t+1$
such that all these paths are internally vertex disjoint from each other, and each of these paths internally avoids
![]() $V(S_{s,t})$
. This works because the number of vertices to avoid when replacing an edge
$V(S_{s,t})$
. This works because the number of vertices to avoid when replacing an edge
![]() $uv\in E(S_{s,t})$
is at most
$uv\in E(S_{s,t})$
is at most
![]() $1+(2t+1)(|E(S_{s,t})\setminus \{uv\}|)=1+(2t+1)(st-1)$
, and there is a collection of
$1+(2t+1)(|E(S_{s,t})\setminus \{uv\}|)=1+(2t+1)(st-1)$
, and there is a collection of
![]() $\lambda -s\geqslant 1+st(2t+1)$
internally disjoint
$\lambda -s\geqslant 1+st(2t+1)$
internally disjoint
![]() $(u,v)$
-paths in
$(u,v)$
-paths in
![]() $G$
of length between
$G$
of length between
![]() $2$
and
$2$
and
![]() $2t+1$
. Finally, since each leaf of
$2t+1$
. Finally, since each leaf of
![]() $S_{s,t}$
has degree at least
$S_{s,t}$
has degree at least
![]() $\lambda \geqslant 1+s+st(2t+1)$
in
$\lambda \geqslant 1+s+st(2t+1)$
in
![]() $G$
, we can extend each leg of the spider thus constructed by one further vertex by adding a distinct neighbour in
$G$
, we can extend each leg of the spider thus constructed by one further vertex by adding a distinct neighbour in
![]() $G$
of each leaf of
$G$
of each leaf of
![]() $S_{s,t}$
. We obtain
$S_{s,t}$
. We obtain
![]() $S_{s,2t+1}$
as a subgraph of
$S_{s,2t+1}$
as a subgraph of
![]() $G$
, a contradiction.
$G$
, a contradiction.
Lemma 33.
There exists a function
![]() $f$
such that for all
$f$
such that for all
![]() $c,k,s,t,\lambda,\gamma \in{\mathbb{N}}$
, if a graph
$c,k,s,t,\lambda,\gamma \in{\mathbb{N}}$
, if a graph
![]() $G$
has treewidth at most
$G$
has treewidth at most
![]() $k$
and no
$k$
and no
![]() $S_{s,t}$
subgraph, and
$S_{s,t}$
subgraph, and
![]() $\textrm{tpw}_c(G^{(\lambda )}) \leqslant \gamma$
, then
$\textrm{tpw}_c(G^{(\lambda )}) \leqslant \gamma$
, then
![]() $\textrm{tpw}_{c+1}(G) \leqslant f(c,k,s,t,\lambda,\gamma )$
.
$\textrm{tpw}_{c+1}(G) \leqslant f(c,k,s,t,\lambda,\gamma )$
.
Proof. Let
![]() $d \,:\!=\, st$
,
$d \,:\!=\, st$
,
![]() $\Delta \,:\!=\, s\cdot \big(1+\lambda ^{2t}\big)$
,
$\Delta \,:\!=\, s\cdot \big(1+\lambda ^{2t}\big)$
,
![]() $m \,:\!=\, \big(1+\Delta ^{d}\big)\cdot \gamma ^{c+1}$
and
$m \,:\!=\, \big(1+\Delta ^{d}\big)\cdot \gamma ^{c+1}$
and
![]() $n \,:\!=\, (k+1)m$
. Let
$n \,:\!=\, (k+1)m$
. Let
![]() $\beta \,:\!=\, (V_h \,:\, h\in V(H))$
be an
$\beta \,:\!=\, (V_h \,:\, h\in V(H))$
be an
![]() $H$
-partition of
$H$
-partition of
![]() $G^{(\lambda )}$
with width at most
$G^{(\lambda )}$
with width at most
![]() $\gamma$
, where
$\gamma$
, where
![]() $\textrm{tw}(H) \leqslant c$
. We show that
$\textrm{tw}(H) \leqslant c$
. We show that
![]() $\beta$
is a
$\beta$
is a
![]() $(c+1, n)$
-disjointed
$(c+1, n)$
-disjointed
![]() $\gamma$
-covering of
$\gamma$
-covering of
![]() $G$
. By Corollary 10,
$G$
. By Corollary 10,
![]() $G$
has
$G$
has
![]() $(c+1)$
-tree-partition-width at most
$(c+1)$
-tree-partition-width at most
![]() $f(c,k,s,t,\lambda,\gamma )\,:\!=\, 2 (c+1)\cdot n\cdot \gamma (12 k)^c.$
$f(c,k,s,t,\lambda,\gamma )\,:\!=\, 2 (c+1)\cdot n\cdot \gamma (12 k)^c.$
Consider distinct
![]() $V_1,\dotsc, V_{c+1} \in \beta$
and a connected component
$V_1,\dotsc, V_{c+1} \in \beta$
and a connected component
![]() $X$
of
$X$
of
![]() $G -(V_1 \cup \dotsb \cup V_{c+1})$
. Let
$G -(V_1 \cup \dotsb \cup V_{c+1})$
. Let
![]() $\mathcal{F}$
be the collection of connected subgraphs in
$\mathcal{F}$
be the collection of connected subgraphs in
![]() $X$
that intersect
$X$
that intersect
![]() $N_G(V_i)$
for each
$N_G(V_i)$
for each
![]() $i\in \{1,\dotsc,c+1\}$
. Let
$i\in \{1,\dotsc,c+1\}$
. Let
![]() $\mathcal{R}^{\prime}$
be a maximum-sized set of vertex-disjoint elements of
$\mathcal{R}^{\prime}$
be a maximum-sized set of vertex-disjoint elements of
![]() $\mathcal{F}$
. By Lemma 16, it suffices to show that
$\mathcal{F}$
. By Lemma 16, it suffices to show that
![]() $|\mathcal{R}^{\prime}|\lt m$
.
$|\mathcal{R}^{\prime}|\lt m$
.
We make two simplifying assumptions. First, we may assume that each
![]() $V_{i}$
consists of a single vertex at the cost of a factor of
$V_{i}$
consists of a single vertex at the cost of a factor of
![]() $\gamma ^{c+1}$
: by averaging over all
$\gamma ^{c+1}$
: by averaging over all
![]() $(c+1)$
-tuples in
$(c+1)$
-tuples in
![]() $V_1\times \dotsb \times V_{c+1}$
, there is one such tuple
$V_1\times \dotsb \times V_{c+1}$
, there is one such tuple
![]() $(x_1, \dotsc, x_{c+1})$
and a subset
$(x_1, \dotsc, x_{c+1})$
and a subset
![]() $\mathcal{R}\subset \mathcal{R}^{\prime}$
such that
$\mathcal{R}\subset \mathcal{R}^{\prime}$
such that
![]() $|\mathcal{R}^{\prime}|\leqslant \gamma ^{c+1}|\mathcal{R}|$
and
$|\mathcal{R}^{\prime}|\leqslant \gamma ^{c+1}|\mathcal{R}|$
and
![]() $N_{G}(x_i) \cap V(R) \neq \varnothing$
for each
$N_{G}(x_i) \cap V(R) \neq \varnothing$
for each
![]() $R\in \mathcal{R}$
and
$R\in \mathcal{R}$
and
![]() $i\in \{1,\dotsc, c+1\}$
. Thus it suffices to show that
$i\in \{1,\dotsc, c+1\}$
. Thus it suffices to show that
![]() $|\mathcal{R}|\leqslant 1+\Delta ^{d}$
. Second, we may assume that
$|\mathcal{R}|\leqslant 1+\Delta ^{d}$
. Second, we may assume that
![]() $\bigcup \{V(R) \,:\, R\in \mathcal{R}\}=V(X)$
.
$\bigcup \{V(R) \,:\, R\in \mathcal{R}\}=V(X)$
.
Let
![]() $X^{\prime}$
be the quotient graph of
$X^{\prime}$
be the quotient graph of
![]() $\mathcal{R}$
(with respect to
$\mathcal{R}$
(with respect to
![]() $X$
). If
$X$
). If
![]() $|V(X^{\prime})|\lt \lambda$
, then we are done. Thus we may assume that
$|V(X^{\prime})|\lt \lambda$
, then we are done. Thus we may assume that
![]() $|V(X^{\prime})| \geqslant \lambda$
and so the vertices
$|V(X^{\prime})| \geqslant \lambda$
and so the vertices
![]() $\{x_1,\dotsc, x_{c+1}\}$
form a
$\{x_1,\dotsc, x_{c+1}\}$
form a
![]() $(c+1)$
-clique in
$(c+1)$
-clique in
![]() $G^{(\lambda )}$
. To show that
$G^{(\lambda )}$
. To show that
![]() $|\mathcal{R}|=|V(X^{\prime})|\leqslant 1+\Delta ^{d}$
, we use the well-known fact that every graph with diameter less than
$|\mathcal{R}|=|V(X^{\prime})|\leqslant 1+\Delta ^{d}$
, we use the well-known fact that every graph with diameter less than
![]() $d$
and maximum degree
$d$
and maximum degree
![]() $\Delta$
has at most
$\Delta$
has at most
![]() $1+\Delta ^{d}$
vertices [Reference Miller and Širáň55].
$1+\Delta ^{d}$
vertices [Reference Miller and Širáň55].
Claim 2.
![]() $X^{\prime}$
contains no path on
$X^{\prime}$
contains no path on
![]() $d$
vertices and thus has diameter less than
$d$
vertices and thus has diameter less than
![]() $d$
.
$d$
.
Proof. For the sake of contradiction, suppose that
![]() $X^{\prime}$
contains a path
$X^{\prime}$
contains a path
![]() $P^{\prime}=(R_0,\dotsc,R_{d-1})$
on
$P^{\prime}=(R_0,\dotsc,R_{d-1})$
on
![]() $d$
vertices. Consider the vertex-disjoint paths
$d$
vertices. Consider the vertex-disjoint paths
![]() $\big(P_j^{\prime} \,:\, j\in \{1,\dotsc, s\}\big)$
in
$\big(P_j^{\prime} \,:\, j\in \{1,\dotsc, s\}\big)$
in
![]() $X^{\prime}$
where
$X^{\prime}$
where
![]() $P^{\prime}_j\,:\!=\, \big(R_{(j-1)t}, \dotsc, R_{jt}\big)$
. For each
$P^{\prime}_j\,:\!=\, \big(R_{(j-1)t}, \dotsc, R_{jt}\big)$
. For each
![]() $j\in \{1,\dotsc,s\}$
fix
$j\in \{1,\dotsc,s\}$
fix
![]() $u_{j}\in V\big(R_{(j-1)t}\big)\cap N_G(x_1)$
. Then there is a
$u_{j}\in V\big(R_{(j-1)t}\big)\cap N_G(x_1)$
. Then there is a
![]() $(u_j,v_j)$
-path
$(u_j,v_j)$
-path
![]() $P_j$
in
$P_j$
in
![]() $X\big[\bigcup \big(V(R) \,:\, R\in V\big(P^{\prime}_j\big)\big)\big]$
of length at least
$X\big[\bigcup \big(V(R) \,:\, R\in V\big(P^{\prime}_j\big)\big)\big]$
of length at least
![]() $t-1$
for some vertex
$t-1$
for some vertex
![]() $v_j\in V\big(R_{jt}\big)$
. Since the paths
$v_j\in V\big(R_{jt}\big)$
. Since the paths
![]() $\big(P_j\,:\, j\in \{1,\dotsc, s\}\big)$
are pairwise vertex-disjoint, it follows that
$\big(P_j\,:\, j\in \{1,\dotsc, s\}\big)$
are pairwise vertex-disjoint, it follows that
![]() $G\big[\{x_1\} \cup \bigcup \big(V(P_j) \,:\, j \in \{1,\dots,s\}\big)\big]$
contains
$G\big[\{x_1\} \cup \bigcup \big(V(P_j) \,:\, j \in \{1,\dots,s\}\big)\big]$
contains
![]() $S_{s,t}$
(see Figure 3a), a contradiction.
$S_{s,t}$
(see Figure 3a), a contradiction.
It remains to show that
![]() $X^{\prime}$
has maximum degree less than
$X^{\prime}$
has maximum degree less than
![]() $\Delta$
. For the sake of contradiction, suppose that
$\Delta$
. For the sake of contradiction, suppose that
![]() $X^{\prime}$
contains a vertex
$X^{\prime}$
contains a vertex
![]() $R^{\prime}$
with degree at least
$R^{\prime}$
with degree at least
![]() $\Delta$
. Let
$\Delta$
. Let
![]() $R_1,\dotsc,R_{\Delta }$
be neighbours of
$R_1,\dotsc,R_{\Delta }$
be neighbours of
![]() $R^{\prime}$
and for each
$R^{\prime}$
and for each
![]() $i \in \{1,\dotsc,\Delta \}$
, let
$i \in \{1,\dotsc,\Delta \}$
, let
![]() $y_i\in V(R_i)$
be adjacent to some
$y_i\in V(R_i)$
be adjacent to some
![]() $w_i\in V(R^{\prime})$
. Let
$w_i\in V(R^{\prime})$
. Let
![]() $L\,:\!=\,\{y_i \,:\, i\in \{1,\dotsc,\Delta \}\}$
and let
$L\,:\!=\,\{y_i \,:\, i\in \{1,\dotsc,\Delta \}\}$
and let
![]() $R^*$
be obtained from
$R^*$
be obtained from
![]() $R^{\prime}$
by adding
$R^{\prime}$
by adding
![]() $L$
and
$L$
and
![]() $\{y_{i}w_{i} \,:\, i\in \{1,\dotsc,\Delta \}\}$
. Let
$\{y_{i}w_{i} \,:\, i\in \{1,\dotsc,\Delta \}\}$
. Let
![]() $T$
be a vertex-minimal tree in
$T$
be a vertex-minimal tree in
![]() $R^*$
such that
$R^*$
such that
![]() $L\subseteq V(T)$
. Then
$L\subseteq V(T)$
. Then
![]() $L$
is precisely the set of leaves of
$L$
is precisely the set of leaves of
![]() $T$
.
$T$
.

Figure 3. Finding spiders and cliques in the proof of Lemma 33.
Claim 3.
![]() $T$
has maximum degree less than
$T$
has maximum degree less than
![]() $\lambda$
.
$\lambda$
.
Proof. For the sake of contradiction, suppose there is a vertex
![]() $v\in V(T)$
with degree (in
$v\in V(T)$
with degree (in
![]() $T$
) at least
$T$
) at least
![]() $\lambda$
. Then there exists a set of
$\lambda$
. Then there exists a set of
![]() $\lambda$
internally vertex-disjoint paths from
$\lambda$
internally vertex-disjoint paths from
![]() $v$
to distinct leaves
$v$
to distinct leaves
![]() $y_1,\dotsc, y_\lambda$
in
$y_1,\dotsc, y_\lambda$
in
![]() $T$
. Then for each
$T$
. Then for each
![]() $i\in \{1,\dotsc, c+1\}$
and
$i\in \{1,\dotsc, c+1\}$
and
![]() $j\in \{1, \dotsc, \lambda \}$
, since
$j\in \{1, \dotsc, \lambda \}$
, since
![]() $R_j$
is connected, there is an
$R_j$
is connected, there is an
![]() $\big(x_i,y_j\big)$
-path in
$\big(x_i,y_j\big)$
-path in
![]() $G[V(R_j)\cup \{x_i\}]$
. As such, there exists
$G[V(R_j)\cup \{x_i\}]$
. As such, there exists
![]() $\lambda$
internally disjoint
$\lambda$
internally disjoint
![]() $(v,x_i)$
-paths in
$(v,x_i)$
-paths in
![]() $G$
for each
$G$
for each
![]() $i\in \{1,\dots,c+1\}$
(see Figure 3b). Thus
$i\in \{1,\dots,c+1\}$
(see Figure 3b). Thus
![]() $vx_i\in E(G^{(\lambda )})$
. So
$vx_i\in E(G^{(\lambda )})$
. So
![]() $\{x_1,\dots,x_{c+1},v\}$
is a
$\{x_1,\dots,x_{c+1},v\}$
is a
![]() $(c+2)$
-clique in
$(c+2)$
-clique in
![]() $G^{(\lambda )}$
. However, as each vertex of this clique belongs to a different part in
$G^{(\lambda )}$
. However, as each vertex of this clique belongs to a different part in
![]() $\beta$
, it follows that
$\beta$
, it follows that
![]() $H$
contains a
$H$
contains a
![]() $(c+2)$
-clique, which contradicts
$(c+2)$
-clique, which contradicts
![]() $\textrm{tw}(H)\leqslant c$
.
$\textrm{tw}(H)\leqslant c$
.
Thus, balls of radius
![]() $r$
(in
$r$
(in
![]() $T$
) have fewer than
$T$
) have fewer than
![]() $1+\lambda ^{r}$
elements. Since
$1+\lambda ^{r}$
elements. Since
![]() $|L|=\Delta = s\cdot \big(1+\lambda ^{2t}\big)$
, there are vertices
$|L|=\Delta = s\cdot \big(1+\lambda ^{2t}\big)$
, there are vertices
![]() $y_1,\dotsc, y_s\in L$
whose balls of radius
$y_1,\dotsc, y_s\in L$
whose balls of radius
![]() $t$
in
$t$
in
![]() $T$
are pairwise disjoint. Let
$T$
are pairwise disjoint. Let
![]() $u_i\in V(R_i)\cap N_G(x_1)$
and let
$u_i\in V(R_i)\cap N_G(x_1)$
and let
![]() $v_i\in V(T)$
be a vertex with distance (in
$v_i\in V(T)$
be a vertex with distance (in
![]() $T$
) exactly
$T$
) exactly
![]() $t$
from
$t$
from
![]() $y_i$
. By construction, there exists a set of disjoint paths
$y_i$
. By construction, there exists a set of disjoint paths
![]() $(P_i \,:\, i\in \{1,\dots,s\})$
such that
$(P_i \,:\, i\in \{1,\dots,s\})$
such that
![]() $P_i$
is a
$P_i$
is a
![]() $(u_i,v_i)$
-path of length at least
$(u_i,v_i)$
-path of length at least
![]() $t$
. Then,
$t$
. Then,
![]() $G[\{x_1\}\cup \bigcup (V(P_i) \,:\, i\in \{1,\dots,s\})]$
contains
$G[\{x_1\}\cup \bigcup (V(P_i) \,:\, i\in \{1,\dots,s\})]$
contains
![]() $S_{s,t}$
(see Figure 3c), a contradiction. Thus
$S_{s,t}$
(see Figure 3c), a contradiction. Thus
![]() $X^{\prime}$
has maximum degree less than
$X^{\prime}$
has maximum degree less than
![]() $\Delta$
.
$\Delta$
.
Lemma 34. For each
![]() $n \in{\mathbb{N}}$
with
$n \in{\mathbb{N}}$
with
![]() $n\geqslant 3$
, the underlying treewidth of
$n\geqslant 3$
, the underlying treewidth of
![]() $\mathcal{G}_{P_n}$
equals
$\mathcal{G}_{P_n}$
equals
![]() $\lfloor{\log{n}}\rfloor - 1$
.
$\lfloor{\log{n}}\rfloor - 1$
.
Proof. Let
![]() $c\,:\!=\, \lfloor{\log{n}}\rfloor$
. For the lower bound, Lemma 12 (ii) and (vii) imply that
$c\,:\!=\, \lfloor{\log{n}}\rfloor$
. For the lower bound, Lemma 12 (ii) and (vii) imply that
![]() $\{C_{c-1,\ell }\,:\, \ell \in{\mathbb{N}}\}$
has underlying treewidth at least
$\{C_{c-1,\ell }\,:\, \ell \in{\mathbb{N}}\}$
has underlying treewidth at least
![]() $c-1$
and is a subset of
$c-1$
and is a subset of
![]() $\mathcal{G}_{P_{n}}$
. The lower bound follows.
$\mathcal{G}_{P_{n}}$
. The lower bound follows.
We prove the upper bound by induction on
![]() $c\geqslant 1$
with the hypothesis that there is a non-decreasing function
$c\geqslant 1$
with the hypothesis that there is a non-decreasing function
![]() $f$
such that every
$f$
such that every
![]() $P_{2^{c+1}-1}$
-free graph
$P_{2^{c+1}-1}$
-free graph
![]() $G$
has
$G$
has
![]() $(c-1)$
-tree-partition-width at most
$(c-1)$
-tree-partition-width at most
![]() $f(\textrm{tw}(G),c)$
. Since
$f(\textrm{tw}(G),c)$
. Since
![]() $P_n\subseteq P_{2^{c+1}-1}$
, the claim follows. We make no attempt to optimise
$P_n\subseteq P_{2^{c+1}-1}$
, the claim follows. We make no attempt to optimise
![]() $f$
. When
$f$
. When
![]() $c=1$
,
$c=1$
,
![]() $G$
contains no
$G$
contains no
![]() $P_3$
and so each component has at most two vertices. Therefore,
$P_3$
and so each component has at most two vertices. Therefore,
![]() $\textrm{tpw}_0(G)\leqslant f(\textrm{tw}(G),1) \,:\!=\, 2$
.
$\textrm{tpw}_0(G)\leqslant f(\textrm{tw}(G),1) \,:\!=\, 2$
.
Now assume
![]() $c\geqslant 2$
and the lemma holds for
$c\geqslant 2$
and the lemma holds for
![]() $c-1$
. Let
$c-1$
. Let
![]() $G$
be a graph with no
$G$
be a graph with no
![]() $P_{2^{c+1}-1}$
and let
$P_{2^{c+1}-1}$
and let
![]() $\lambda \,:\!=\, \max \{3+(2^{c}-2)(2^{c}-1), \textrm{tw}(G)+1\}$
. By Lemmas 31 and 32,
$\lambda \,:\!=\, \max \{3+(2^{c}-2)(2^{c}-1), \textrm{tw}(G)+1\}$
. By Lemmas 31 and 32,
![]() $G^{(\lambda )}$
has treewidth at most
$G^{(\lambda )}$
has treewidth at most
![]() $\textrm{tw}(G)$
and contains no
$\textrm{tw}(G)$
and contains no
![]() $P_{2^{c}-1}$
. By induction,
$P_{2^{c}-1}$
. By induction,
![]() $\textrm{tpw}_{c-2}(G^{(\lambda )}) \leqslant \gamma \,:\!=\, f(\textrm{tw}(G),c-1)$
. By Lemma 33,
$\textrm{tpw}_{c-2}(G^{(\lambda )}) \leqslant \gamma \,:\!=\, f(\textrm{tw}(G),c-1)$
. By Lemma 33,
![]() $\textrm{tpw}_{c+1}(G) \leqslant f(\textrm{tw}(G),c)\,:\!=\, \tilde{f}(c,\textrm{tw}(G),2,2^{c}-1,\lambda,\gamma )$
where
$\textrm{tpw}_{c+1}(G) \leqslant f(\textrm{tw}(G),c)\,:\!=\, \tilde{f}(c,\textrm{tw}(G),2,2^{c}-1,\lambda,\gamma )$
where
![]() $\tilde{f}$
is from Lemma 33, as required.
$\tilde{f}$
is from Lemma 33, as required.
Lemma 34 proves (ii) in Theorem 29.
To prove (iv) in Theorem 29, we need the following lower bound result.
Lemma 35. For all
![]() $c\in{\mathbb{N}}$
, there exists an
$c\in{\mathbb{N}}$
, there exists an
![]() $S_{3,2^c}$
-free graph class
$S_{3,2^c}$
-free graph class
![]() $\{J_{c,N} \,:\, N\in{\mathbb{N}}\}$
with underlying treewidth
$\{J_{c,N} \,:\, N\in{\mathbb{N}}\}$
with underlying treewidth
![]() $c+1$
.
$c+1$
.
Proof. Let
![]() $J_{c,N}$
be the graph obtained from a path
$J_{c,N}$
be the graph obtained from a path
![]() $P_{N+1}=(p_1,\ldots, p_{N+1})$
where for each edge
$P_{N+1}=(p_1,\ldots, p_{N+1})$
where for each edge
![]() $p_{i}p_{i+1}\in E(P_{n+1})$
, we add a copy
$p_{i}p_{i+1}\in E(P_{n+1})$
, we add a copy
![]() $X_{i}$
of
$X_{i}$
of
![]() $(2N-1)C_{c-1,N}$
and let
$(2N-1)C_{c-1,N}$
and let
![]() $p_i$
and
$p_i$
and
![]() $p_{i+1}$
dominate
$p_{i+1}$
dominate
![]() $X_{i}$
(see Figure 4; this construction also provides a lower bound on the clustered chromatic number [Reference Norin, Scott, Seymour and Wood58]). To prove the lemma, it suffices to show that
$X_{i}$
(see Figure 4; this construction also provides a lower bound on the clustered chromatic number [Reference Norin, Scott, Seymour and Wood58]). To prove the lemma, it suffices to show that
![]() $J_{c,N}$
is
$J_{c,N}$
is
![]() $S_{3,2^c}$
-free,
$S_{3,2^c}$
-free,
![]() $\textrm{tw}(J_{c,N})=c+1$
and
$\textrm{tw}(J_{c,N})=c+1$
and
![]() $\textrm{tpw}_c(J_{c,N})\gt N$
.
$\textrm{tpw}_c(J_{c,N})\gt N$
.

Figure 4. Construction of
![]() $J_{c,N}$
.
$J_{c,N}$
.
The claimed treewidth of
![]() $J_{c,N}$
holds since
$J_{c,N}$
holds since
![]() $\textrm{tw}((2N-1)C_{c-1,N})=c-1$
(Lemma 12 (i)), and the two dominant vertices for each copy of
$\textrm{tw}((2N-1)C_{c-1,N})=c-1$
(Lemma 12 (i)), and the two dominant vertices for each copy of
![]() $(2N-1)C_{c-1,N}$
give
$(2N-1)C_{c-1,N}$
give
![]() $\textrm{tw}(J_{c,N})=c+1$
. Now suppose, for the sake of contradiction, that
$\textrm{tw}(J_{c,N})=c+1$
. Now suppose, for the sake of contradiction, that
![]() $S_{3,2^c}$
is a subgraph of
$S_{3,2^c}$
is a subgraph of
![]() $J_{c,N}$
with centre
$J_{c,N}$
with centre
![]() $v\in V(J_{c,N})$
. Observe that
$v\in V(J_{c,N})$
. Observe that
![]() $v$
has at most two neighbours
$v$
has at most two neighbours
![]() $p_i$
and
$p_i$
and
![]() $p_j$
in
$p_j$
in
![]() $P_N$
. Moreover, each neighbour of
$P_N$
. Moreover, each neighbour of
![]() $v$
in
$v$
in
![]() $J_{c,N}\setminus \{v,p_i,p_j\}$
is contained in a component that is a subgraph of
$J_{c,N}\setminus \{v,p_i,p_j\}$
is contained in a component that is a subgraph of
![]() $C_{c-1,N}$
. Since
$C_{c-1,N}$
. Since
![]() $S_{3,2^c}$
has three legs, one of the legs must be contained in a copy of
$S_{3,2^c}$
has three legs, one of the legs must be contained in a copy of
![]() $C_{c-1,N}$
which contradicts
$C_{c-1,N}$
which contradicts
![]() $C_{c-1,N}$
not having a path on
$C_{c-1,N}$
not having a path on
![]() $2^{c}$
vertices (Lemma 12 (vii)).
$2^{c}$
vertices (Lemma 12 (vii)).
It remains to show that
![]() $\textrm{tpw}_c(J_{c,N})\gt N$
. For the sake of contradiction, suppose that
$\textrm{tpw}_c(J_{c,N})\gt N$
. For the sake of contradiction, suppose that
![]() $J_{c,N}$
has a
$J_{c,N}$
has a
![]() $c$
-tree-partition
$c$
-tree-partition
![]() $\beta \,:\!=\,(V_h \,:\, h\in V(H))$
with width at most
$\beta \,:\!=\,(V_h \,:\, h\in V(H))$
with width at most
![]() $N$
. Since
$N$
. Since
![]() $|V(P_{N+1})|=N+1$
, there exists an edge
$|V(P_{N+1})|=N+1$
, there exists an edge
![]() $p_ip_{i+1}\in E(P_{N+1})$
such that
$p_ip_{i+1}\in E(P_{N+1})$
such that
![]() $p_i$
and
$p_i$
and
![]() $p_{i+1}$
belong to different parts in
$p_{i+1}$
belong to different parts in
![]() $\beta$
. Let
$\beta$
. Let
![]() $V_i$
and
$V_i$
and
![]() $V_{i+1}$
be such that
$V_{i+1}$
be such that
![]() $p_i\in V_i$
and
$p_i\in V_i$
and
![]() $p_{i+1}\in V_{i+1}$
. Since
$p_{i+1}\in V_{i+1}$
. Since
![]() $|(V_i\cup V_{i+1})\setminus \{p_i,p_{i-1}\}|\leqslant 2N-2$
, there exists a copy of
$|(V_i\cup V_{i+1})\setminus \{p_i,p_{i-1}\}|\leqslant 2N-2$
, there exists a copy of
![]() $C_{c-1,N}$
in
$C_{c-1,N}$
in
![]() $X_i$
such that
$X_i$
such that
![]() $V(C_{c-1,N})\cap (V_i\cup V_{i+1})=\varnothing$
. By Lemma 12 (ii),
$V(C_{c-1,N})\cap (V_i\cup V_{i+1})=\varnothing$
. By Lemma 12 (ii),
![]() $C_{c-1,N}$
contains a
$C_{c-1,N}$
contains a
![]() $c$
-clique whose vertices are in different parts in
$c$
-clique whose vertices are in different parts in
![]() $\beta$
. Together with
$\beta$
. Together with
![]() $p_i$
and
$p_i$
and
![]() $p_{i+1}$
, it follows that
$p_{i+1}$
, it follows that
![]() $J_{c,N}$
contains a
$J_{c,N}$
contains a
![]() $(c+2)$
-clique whose vertices are in different parts in
$(c+2)$
-clique whose vertices are in different parts in
![]() $\beta$
. Thus
$\beta$
. Thus
![]() $H$
has a
$H$
has a
![]() $(c+2)$
-clique, a contradiction.
$(c+2)$
-clique, a contradiction.
Lemma 36. For all
![]() $s,t \in{\mathbb{N}}$
where
$s,t \in{\mathbb{N}}$
where
![]() $s\geqslant 3$
, the underlying treewidth of
$s\geqslant 3$
, the underlying treewidth of
![]() $\mathcal{G}_{S_{s,t}}$
is
$\mathcal{G}_{S_{s,t}}$
is
![]() $\lfloor{\log{t}}\rfloor + 1$
.
$\lfloor{\log{t}}\rfloor + 1$
.
Proof. Let
![]() $c \,:\!=\, \lfloor{\log{t}}\rfloor$
. For the lower bound,
$c \,:\!=\, \lfloor{\log{t}}\rfloor$
. For the lower bound,
![]() $\mathcal{G}_{S_{3,2^{c}}}$
has underlying treewidth at least
$\mathcal{G}_{S_{3,2^{c}}}$
has underlying treewidth at least
![]() $c+1$
by Lemma 35. Since
$c+1$
by Lemma 35. Since
![]() $S_{3,2^{c}}\subseteq S_{s,t}$
, it follows that
$S_{3,2^{c}}\subseteq S_{s,t}$
, it follows that
![]() $\mathcal{G}_{S_{3,2^{c}}}\subseteq \mathcal{G}_{S_{s,t}}$
, which implies the lower bound.
$\mathcal{G}_{S_{3,2^{c}}}\subseteq \mathcal{G}_{S_{s,t}}$
, which implies the lower bound.
We prove the upper bound by induction on
![]() $c\in{\mathbb{N}}_0$
with the following hypothesis: There is an increasing function
$c\in{\mathbb{N}}_0$
with the following hypothesis: There is an increasing function
![]() $f$
such that for each
$f$
such that for each
![]() $s\in{\mathbb{N}}$
, every
$s\in{\mathbb{N}}$
, every
![]() $S_{s,2^{c+1}-1}$
-free graph
$S_{s,2^{c+1}-1}$
-free graph
![]() $G$
has
$G$
has
![]() $(c+1)$
-tree-partition-width at most
$(c+1)$
-tree-partition-width at most
![]() $f(\textrm{tw}(G),c,s)$
. Since
$f(\textrm{tw}(G),c,s)$
. Since
![]() $S_{s,t}\subseteq S_{s,2^{c+1}-1}$
, the claim follows. When
$S_{s,t}\subseteq S_{s,2^{c+1}-1}$
, the claim follows. When
![]() $c=0$
,
$c=0$
,
![]() $G$
has maximum degree at most
$G$
has maximum degree at most
![]() $s-1$
, and
$s-1$
, and
![]() $G$
has
$G$
has
![]() $1$
-tree-partition-width at most
$1$
-tree-partition-width at most
![]() $f(\textrm{tw}(G),0,s) \,:\!=\, 24(\textrm{tw}(G)+1)(s-1)$
by Lemma 2.
$f(\textrm{tw}(G),0,s) \,:\!=\, 24(\textrm{tw}(G)+1)(s-1)$
by Lemma 2.
Now assume
![]() $c\geqslant 1$
and the lemma holds for
$c\geqslant 1$
and the lemma holds for
![]() $c-1$
. Let
$c-1$
. Let
![]() $G$
be an
$G$
be an
![]() $(s,2^{c+1}-1)$
-spider-free graph and let
$(s,2^{c+1}-1)$
-spider-free graph and let
![]() $\lambda \,:\!=\, \max \{1+s+st(2t+1), \textrm{tw}(G)+1\}$
. By Lemmas 31 and 32,
$\lambda \,:\!=\, \max \{1+s+st(2t+1), \textrm{tw}(G)+1\}$
. By Lemmas 31 and 32,
![]() $\textrm{tw}(G^{(\lambda )}) \leqslant \textrm{tw}(G)$
and
$\textrm{tw}(G^{(\lambda )}) \leqslant \textrm{tw}(G)$
and
![]() $G^{(\lambda )}$
contains no
$G^{(\lambda )}$
contains no
![]() $S_{s,2^{c}-1}$
. By induction,
$S_{s,2^{c}-1}$
. By induction,
![]() $\textrm{tpw}_c(G^{(\lambda )}) \leqslant \gamma \,:\!=\, f(\textrm{tw}(G),c, s)$
. By Lemma 33,
$\textrm{tpw}_c(G^{(\lambda )}) \leqslant \gamma \,:\!=\, f(\textrm{tw}(G),c, s)$
. By Lemma 33,
![]() $\textrm{tpw}_{c+1}(G) \leqslant f(\textrm{tw}(G),c, s)\,:\!=\, \tilde{f}(c,\textrm{tw}(G),s,2^{c+1}-1,\lambda,\gamma )$
where
$\textrm{tpw}_{c+1}(G) \leqslant f(\textrm{tw}(G),c, s)\,:\!=\, \tilde{f}(c,\textrm{tw}(G),s,2^{c+1}-1,\lambda,\gamma )$
where
![]() $\tilde{f}$
is from Lemma 33, as required.
$\tilde{f}$
is from Lemma 33, as required.
Lemma 36 proves (iv) in Theorem 29.
Lemma 37. For every connected graph
![]() $H$
and
$H$
and
![]() $\ell \in{\mathbb{N}}$
where
$\ell \in{\mathbb{N}}$
where
![]() $\ell \geqslant 2$
, if
$\ell \geqslant 2$
, if
![]() $\mathcal{G}_H$
has underlying treewidth
$\mathcal{G}_H$
has underlying treewidth
![]() $c$
then
$c$
then
![]() $\mathcal{G}_{\ell \, H}$
has underlying treewidth
$\mathcal{G}_{\ell \, H}$
has underlying treewidth
![]() $c+1$
.
$c+1$
.
Proof. We first prove the lower bound. Since
![]() $\mathcal{G}_H$
has underlying treewidth
$\mathcal{G}_H$
has underlying treewidth
![]() $c$
, there exists
$c$
, there exists
![]() $k\in{\mathbb{N}}$
such that for all
$k\in{\mathbb{N}}$
such that for all
![]() $j\in{\mathbb{N}}$
, there is a graph
$j\in{\mathbb{N}}$
, there is a graph
![]() $G_j\in \mathcal{G}_H$
with
$G_j\in \mathcal{G}_H$
with
![]() $\textrm{tw}(G_j)=k$
and
$\textrm{tw}(G_j)=k$
and
![]() $\textrm{tpw}_{c-1}(G_j)\gt j$
. Consider the graph class
$\textrm{tpw}_{c-1}(G_j)\gt j$
. Consider the graph class
![]() $\mathcal{J}\,:\!=\,\{\widehat{j\,G_j} \,:\, j\in{\mathbb{N}}\}.$
Observe that every graph in
$\mathcal{J}\,:\!=\,\{\widehat{j\,G_j} \,:\, j\in{\mathbb{N}}\}.$
Observe that every graph in
![]() $\mathcal{J}$
is
$\mathcal{J}$
is
![]() $\ell \,H$
-free, so
$\ell \,H$
-free, so
![]() $\mathcal{J}\subseteq \mathcal{G}_{\ell \, H}$
. Moreover, since adding a dominant vertex increase the treewidth of a graph by
$\mathcal{J}\subseteq \mathcal{G}_{\ell \, H}$
. Moreover, since adding a dominant vertex increase the treewidth of a graph by
![]() $1$
,
$1$
,
![]() $\textrm{tw}(\widehat{j\,G_j})=k+1$
for all
$\textrm{tw}(\widehat{j\,G_j})=k+1$
for all
![]() $j\in{\mathbb{N}}$
. Finally, consider a
$j\in{\mathbb{N}}$
. Finally, consider a
![]() $j$
-partition
$j$
-partition
![]() $\beta \,:\!=\,(V_x\,:\, x \in V(J))$
of
$\beta \,:\!=\,(V_x\,:\, x \in V(J))$
of
![]() $\widehat{j\, G_j}$
. At most
$\widehat{j\, G_j}$
. At most
![]() $j - 1$
copies of
$j - 1$
copies of
![]() $G_j$
contain a vertex in the same part
$G_j$
contain a vertex in the same part
![]() $V_y$
as the dominant vertex
$V_y$
as the dominant vertex
![]() $v$
. Thus, some copy
$v$
. Thus, some copy
![]() $G$
of
$G$
of
![]() $G_j$
contains no vertex in
$G_j$
contains no vertex in
![]() $V_y$
. Consider the sub-partition
$V_y$
. Consider the sub-partition
![]() $\beta ^{\prime}\,:\!=\,(V_x\cap V(G)\,:\, x \in V(J^{\prime}))$
of
$\beta ^{\prime}\,:\!=\,(V_x\cap V(G)\,:\, x \in V(J^{\prime}))$
of
![]() $G$
where
$G$
where
![]() $J^{\prime}\subseteq J$
. Since
$J^{\prime}\subseteq J$
. Since
![]() $\beta ^{\prime}$
has width at most
$\beta ^{\prime}$
has width at most
![]() $j$
,
$j$
,
![]() $J^{\prime}$
has treewidth at least
$J^{\prime}$
has treewidth at least
![]() $c$
and so
$c$
and so
![]() $J[V(J^{\prime})\cup \{y\}]$
has treewidth at least
$J[V(J^{\prime})\cup \{y\}]$
has treewidth at least
![]() $c+1$
. Thus
$c+1$
. Thus
![]() $\mathcal{J}$
has underlying treewidth at least
$\mathcal{J}$
has underlying treewidth at least
![]() $c+1$
.
$c+1$
.
We now prove the upper bound. Let
![]() $G$
be an
$G$
be an
![]() $\ell \, H$
-free graph. Let
$\ell \, H$
-free graph. Let
![]() $A_1,\dots,A_m$
be a maximal set of pairwise disjoint copies of
$A_1,\dots,A_m$
be a maximal set of pairwise disjoint copies of
![]() $H$
in
$H$
in
![]() $G$
. Then
$G$
. Then
![]() $m\lt \ell$
. Let
$m\lt \ell$
. Let
![]() $B \,:\!=\, G-V(A_1\cup \dots \cup A_m)$
. By the maximality of
$B \,:\!=\, G-V(A_1\cup \dots \cup A_m)$
. By the maximality of
![]() $m$
,
$m$
,
![]() $B$
is
$B$
is
![]() $H$
-free. Thus
$H$
-free. Thus
![]() $B$
has a
$B$
has a
![]() $c$
-tree-partition
$c$
-tree-partition
![]() $(V_x \,:\, x\in V(J^{\prime}))$
with width at most
$(V_x \,:\, x\in V(J^{\prime}))$
with width at most
![]() $\tilde{f}(\textrm{tw}(B))$
for some function
$\tilde{f}(\textrm{tw}(B))$
for some function
![]() $\tilde{f}$
. Let
$\tilde{f}$
. Let
![]() $J$
be the graph obtained from
$J$
be the graph obtained from
![]() $J^{\prime}$
by adding a dominant vertex
$J^{\prime}$
by adding a dominant vertex
![]() $y$
, and let
$y$
, and let
![]() $V_y \,:\!=\, V(A_1\cup \dots \cup A_n)$
. Then
$V_y \,:\!=\, V(A_1\cup \dots \cup A_n)$
. Then
![]() $(V_x \,:\, x\in V(J))$
is a
$(V_x \,:\, x\in V(J))$
is a
![]() $(c+1)$
-tree-partition of
$(c+1)$
-tree-partition of
![]() $G$
with width at most
$G$
with width at most
![]() $f(\textrm{tw}(G))\,:\!=\, \max \{(\ell -1)|V(H)|,\tilde{f}(1), \dots,\tilde{f}(\textrm{tw}(G))\}$
, as required.
$f(\textrm{tw}(G))\,:\!=\, \max \{(\ell -1)|V(H)|,\tilde{f}(1), \dots,\tilde{f}(\textrm{tw}(G))\}$
, as required.
Lemmas 34, 36 and 37 prove Theorem 29 (iii) and (iv). Since every spider-forest is a subgraph of
![]() $\ell \, S_{s,t}$
for some
$\ell \, S_{s,t}$
for some
![]() $\ell,s,t \in{\mathbb{N}}$
, these results also imply the sufficiency of (i) in Theorem 29.
$\ell,s,t \in{\mathbb{N}}$
, these results also imply the sufficiency of (i) in Theorem 29.
8. Excluding an induced subgraph
For a graph
![]() $H$
, let
$H$
, let
![]() $\mathcal{I}_H$
be the class of graphs with no induced subgraph isomorphic to
$\mathcal{I}_H$
be the class of graphs with no induced subgraph isomorphic to
![]() $H$
. This section characterises the graphs
$H$
. This section characterises the graphs
![]() $H$
such that
$H$
such that
![]() $\mathcal{I}_H$
has bounded underlying treewidth, and determines the precise underlying treewidth for each such
$\mathcal{I}_H$
has bounded underlying treewidth, and determines the precise underlying treewidth for each such
![]() $H$
.
$H$
.
Theorem 38. For any graph
![]() $H$
,
$H$
,
-
(a)
 $\mathcal{I}_H$
has bounded underlying treewidth if and only if
$\mathcal{I}_H$
has bounded underlying treewidth if and only if
 $H$
is a star-forest;
$H$
is a star-forest; -
(b) if
 $H$
is a star-forest, then
$H$
is a star-forest, then
 $\mathcal{I}_H$
has underlying treewidth at most
$\mathcal{I}_H$
has underlying treewidth at most
 $2$
;
$2$
; -
(c)
 $\mathcal{I}_H$
has underlying treewidth at most
$\mathcal{I}_H$
has underlying treewidth at most
 $1$
if and only if
$1$
if and only if
 $H$
is a star or each component of
$H$
is a star or each component of
 $H$
is a path on at most three vertices;
$H$
is a path on at most three vertices; -
(d)
 $\mathcal{I}_H$
has underlying treewidth
$\mathcal{I}_H$
has underlying treewidth
 $0$
if and only if
$0$
if and only if
 $H$
is a path on at most three vertices, or
$H$
is a path on at most three vertices, or
 $E(H) = \varnothing$
.
$E(H) = \varnothing$
.
We prove Theorem 38 by a sequence of lemmas.
Lemma 39. If
![]() $\mathcal{I}_H$
has bounded underlying treewidth, then
$\mathcal{I}_H$
has bounded underlying treewidth, then
![]() $H$
is a star-forest.
$H$
is a star-forest.
Proof. Suppose that
![]() $\mathcal{I}_H$
has underlying treewidth
$\mathcal{I}_H$
has underlying treewidth
![]() $c$
. So
$c$
. So
![]() $\mathcal{G}_H$
has underlying treewidth at most
$\mathcal{G}_H$
has underlying treewidth at most
![]() $c$
(since
$c$
(since
![]() $\mathcal{G}_H \subseteq \mathcal{I}_H$
). Lemma 30 implies that
$\mathcal{G}_H \subseteq \mathcal{I}_H$
). Lemma 30 implies that
![]() $H$
is a spider-forest. By Corollary 14,
$H$
is a spider-forest. By Corollary 14,
![]() $\{C_{c, \ell } \,:\, c, \ell \in{\mathbb{N}}\}$
has unbounded underlying treewidth. Hence,
$\{C_{c, \ell } \,:\, c, \ell \in{\mathbb{N}}\}$
has unbounded underlying treewidth. Hence,
![]() $H$
is an induced subgraph of some
$H$
is an induced subgraph of some
![]() $C_{c, \ell }$
. By Lemma 12,
$C_{c, \ell }$
. By Lemma 12,
![]() $C_{c, \ell }$
has no induced
$C_{c, \ell }$
has no induced
![]() $P_{4}$
and so
$P_{4}$
and so
![]() $H$
contains no induced
$H$
contains no induced
![]() $P_{4}$
. Every spider-forest with no induced
$P_{4}$
. Every spider-forest with no induced
![]() $P_{4}$
is a star-forest. So
$P_{4}$
is a star-forest. So
![]() $H$
is a star-forest.
$H$
is a star-forest.
Lemma 39 proves the necessity of (i) in Theorem 38.
Lemma 40. If
![]() $H$
is a star
$H$
is a star
![]() $K_{1,s}$
, then
$K_{1,s}$
, then
![]() $\mathcal{I}_H$
has underlying treewidth at most
$\mathcal{I}_H$
has underlying treewidth at most
![]() $1$
.
$1$
.
Proof. Say
![]() $G\in \mathcal{I}_H$
. For each vertex
$G\in \mathcal{I}_H$
. For each vertex
![]() $v\in V(G)$
, if
$v\in V(G)$
, if
![]() $G_v \,:\!=\, G[N_G(v)]$
then
$G_v \,:\!=\, G[N_G(v)]$
then
![]() $\alpha (G_v)\leqslant s-1$
and
$\alpha (G_v)\leqslant s-1$
and
![]() $\chi (G_v)\leqslant \textrm{tw}(G_v)+1\leqslant \textrm{tw}(G)$
, implying
$\chi (G_v)\leqslant \textrm{tw}(G_v)+1\leqslant \textrm{tw}(G)$
, implying
![]() $\deg _G(v)= |V(G_v)| \leqslant \chi (G_v)\alpha (G_v)\leqslant \textrm{tw}(G)(s-1)$
. By Lemma 2,
$\deg _G(v)= |V(G_v)| \leqslant \chi (G_v)\alpha (G_v)\leqslant \textrm{tw}(G)(s-1)$
. By Lemma 2,
![]() $\textrm{tpw}(G)\leqslant 24\textrm{tw}(G)^2(s-1)$
. Hence
$\textrm{tpw}(G)\leqslant 24\textrm{tw}(G)^2(s-1)$
. Hence
![]() $\mathcal{I}_H$
has underlying treewidth at most
$\mathcal{I}_H$
has underlying treewidth at most
![]() $1$
.
$1$
.
Lemma 41. If
![]() $H$
is a star-forest, then
$H$
is a star-forest, then
![]() $\mathcal{I}_H$
has underlying treewidth at most
$\mathcal{I}_H$
has underlying treewidth at most
![]() $2$
.
$2$
.
Proof. Say
![]() $H$
has
$H$
has
![]() $\ell$
components, each with at most
$\ell$
components, each with at most
![]() $s$
leaves. Let
$s$
leaves. Let
![]() $G\in \mathcal{I}_H$
. Let
$G\in \mathcal{I}_H$
. Let
![]() $A_1,\dots,A_n$
be a maximal set of pairwise disjoint induced
$A_1,\dots,A_n$
be a maximal set of pairwise disjoint induced
![]() $K_{1,s}$
subgraphs in
$K_{1,s}$
subgraphs in
![]() $G$
. Define
$G$
. Define
![]() $J$
to be the graph obtained from
$J$
to be the graph obtained from
![]() $G[V(A_1\cup \dots \cup A_n)]$
by contracting each
$G[V(A_1\cup \dots \cup A_n)]$
by contracting each
![]() $A_i$
into a vertex
$A_i$
into a vertex
![]() $v_i$
. Then
$v_i$
. Then
![]() $n\leqslant \chi (J)\alpha (J)\leqslant (\textrm{tw}(J)+1)(\ell -1)\leqslant (\textrm{tw}(G)+1)(\ell -1)$
since
$n\leqslant \chi (J)\alpha (J)\leqslant (\textrm{tw}(J)+1)(\ell -1)\leqslant (\textrm{tw}(G)+1)(\ell -1)$
since
![]() $J$
is a minor of
$J$
is a minor of
![]() $G$
. Thus
$G$
. Thus
![]() $|V(A_1\cup \dots \cup A_n)| \leqslant (\textrm{tw}(G)+1)(\ell -1)(s+1)$
. Let
$|V(A_1\cup \dots \cup A_n)| \leqslant (\textrm{tw}(G)+1)(\ell -1)(s+1)$
. Let
![]() $B \,:\!=\, G-V(A_1\cup \dots \cup A_n)$
. By the maximality of
$B \,:\!=\, G-V(A_1\cup \dots \cup A_n)$
. By the maximality of
![]() $n$
,
$n$
,
![]() $B$
contains no induced
$B$
contains no induced
![]() $K_{1,s}$
. As in the proof of Lemma 40,
$K_{1,s}$
. As in the proof of Lemma 40,
![]() $B$
has a tree-partition
$B$
has a tree-partition
![]() $(V_x \,:\, x\in V(T))$
of width at most
$(V_x \,:\, x\in V(T))$
of width at most
![]() $24\textrm{tw}(G)^2(s-1)$
. Let
$24\textrm{tw}(G)^2(s-1)$
. Let
![]() $H$
be the graph obtained from
$H$
be the graph obtained from
![]() $T$
by adding a dominant vertex
$T$
by adding a dominant vertex
![]() $y$
, and let
$y$
, and let
![]() $V_y \,:\!=\, V(A_1\cup \dots \cup A_n)$
. Then
$V_y \,:\!=\, V(A_1\cup \dots \cup A_n)$
. Then
![]() $(V_h \,:\, h\in V(H))$
is a
$(V_h \,:\, h\in V(H))$
is a
![]() $2$
-tree-partition of
$2$
-tree-partition of
![]() $G$
with width at most
$G$
with width at most
![]() $\max \{24\textrm{tw}(G)^2(s-1),(\textrm{tw}(G)+1)(\ell -1)(s+1)\}$
. Hence
$\max \{24\textrm{tw}(G)^2(s-1),(\textrm{tw}(G)+1)(\ell -1)(s+1)\}$
. Hence
![]() $\mathcal{I}_H$
has underlying treewidth at most
$\mathcal{I}_H$
has underlying treewidth at most
![]() $2$
.
$2$
.
Lemma 41 proves (ii) and the sufficiency of (i) in Theorem 38.
Lemma 42. If
![]() $H$
is a forest in which each component is a path on at most three vertices, then
$H$
is a forest in which each component is a path on at most three vertices, then
![]() $\mathcal{I}_H$
has underlying treewidth at most
$\mathcal{I}_H$
has underlying treewidth at most
![]() $1$
.
$1$
.
Proof. Say
![]() $H$
has
$H$
has
![]() $k$
components. Let
$k$
components. Let
![]() $G\in \mathcal{I}_H$
. Let
$G\in \mathcal{I}_H$
. Let
![]() $A_1,\dots,A_n$
be a maximal set of pairwise disjoint induced
$A_1,\dots,A_n$
be a maximal set of pairwise disjoint induced
![]() $P_3$
subgraphs in
$P_3$
subgraphs in
![]() $G$
. Let
$G$
. Let
![]() $J$
be the minor of
$J$
be the minor of
![]() $G$
obtained from
$G$
obtained from
![]() $G[ V(A_1\cup \dots \cup A_n)]$
by contracting each
$G[ V(A_1\cup \dots \cup A_n)]$
by contracting each
![]() $A_i$
into a vertex. Thus
$A_i$
into a vertex. Thus
![]() $n = |V(J)|\leqslant \chi (J)\alpha (J)\leqslant (\textrm{tw}(J)+1)(k-1)\leqslant (\textrm{tw}(G)+1)(k-1)$
. Let
$n = |V(J)|\leqslant \chi (J)\alpha (J)\leqslant (\textrm{tw}(J)+1)(k-1)\leqslant (\textrm{tw}(G)+1)(k-1)$
. Let
![]() $B_1,\dots,B_m$
be the components of
$B_1,\dots,B_m$
be the components of
![]() $G-V(A_1\cup \dots \cup A_n)$
. By the maximality of
$G-V(A_1\cup \dots \cup A_n)$
. By the maximality of
![]() $n$
, each
$n$
, each
![]() $B_i$
has no induced
$B_i$
has no induced
![]() $P_3$
subgraph, so
$P_3$
subgraph, so
![]() $B_i$
is a complete subgraph and
$B_i$
is a complete subgraph and
![]() $|V(B_i)|\leqslant \textrm{tw}(G)+1$
. Let
$|V(B_i)|\leqslant \textrm{tw}(G)+1$
. Let
![]() $T$
be the star with centre
$T$
be the star with centre
![]() $x$
and leaves
$x$
and leaves
![]() $y_1,\dots,y_m$
. Let
$y_1,\dots,y_m$
. Let
![]() $V_x \,:\!=\, V(A_1\cup \dots \cup A_n)$
and
$V_x \,:\!=\, V(A_1\cup \dots \cup A_n)$
and
![]() $V_{y_j} \,:\!=\, V(B_j)$
. So
$V_{y_j} \,:\!=\, V(B_j)$
. So
![]() $(V_h \,:\, h\in V(T))$
is a tree-partition of
$(V_h \,:\, h\in V(T))$
is a tree-partition of
![]() $G$
with width at most
$G$
with width at most
![]() $\max \{3(k-1)(\textrm{tw}(G)+1),\textrm{tw}(G)+1\}$
. Hence
$\max \{3(k-1)(\textrm{tw}(G)+1),\textrm{tw}(G)+1\}$
. Hence
![]() $\mathcal{I}_H$
has underlying treewidth at most
$\mathcal{I}_H$
has underlying treewidth at most
![]() $1$
.
$1$
.
Lemma 43. If
![]() $H$
is a star-forest with at least two components and at least one component of
$H$
is a star-forest with at least two components and at least one component of
![]() $H$
has at least three leaves, then
$H$
has at least three leaves, then
![]() $\mathcal{I}_H$
has underlying treewidth
$\mathcal{I}_H$
has underlying treewidth
![]() $2$
.
$2$
.
Proof. Consider a star
![]() $S$
with at least three leaves that is a subgraph of a fan
$S$
with at least three leaves that is a subgraph of a fan
![]() $F$
with dominant vertex
$F$
with dominant vertex
![]() $v$
. Since
$v$
. Since
![]() $F-v$
has maximum degree
$F-v$
has maximum degree
![]() $2$
,
$2$
,
![]() $v$
is in
$v$
is in
![]() $S$
. Since every vertex of
$S$
. Since every vertex of
![]() $F$
is adjacent to
$F$
is adjacent to
![]() $v$
,
$v$
,
![]() $H$
is not an induced subgraph of
$H$
is not an induced subgraph of
![]() $F$
. By Lemma 12, the class of fan graphs has underlying treewidth
$F$
. By Lemma 12, the class of fan graphs has underlying treewidth
![]() $2$
. Thus
$2$
. Thus
![]() $\mathcal{I}_H$
has underlying treewidth at least
$\mathcal{I}_H$
has underlying treewidth at least
![]() $2$
, with equality by Lemma 41.
$2$
, with equality by Lemma 41.
Lemmas 40, 42 and 43 prove (iii) in Theorem 38.
Lemma 44. If
![]() $E(H)=\varnothing$
or
$E(H)=\varnothing$
or
![]() $H$
is a path on at most three vertices, then
$H$
is a path on at most three vertices, then
![]() $\mathcal{I}_H$
has underlying treewidth
$\mathcal{I}_H$
has underlying treewidth
![]() $0$
.
$0$
.
Proof. First suppose that
![]() $E(H)=\varnothing$
. For each
$E(H)=\varnothing$
. For each
![]() $G\in \mathcal{I}_H$
,
$G\in \mathcal{I}_H$
,
![]() $\{V(G)\}$
is a
$\{V(G)\}$
is a
![]() $0$
-tree-partition of
$0$
-tree-partition of
![]() $G$
with width
$G$
with width
![]() $|V(G)|\leqslant \chi (G)\alpha (G) \leqslant (\textrm{tw}(G)+1)(|V(H)|-1)$
. Hence
$|V(G)|\leqslant \chi (G)\alpha (G) \leqslant (\textrm{tw}(G)+1)(|V(H)|-1)$
. Hence
![]() $\mathcal{I}_H$
has underlying treewidth
$\mathcal{I}_H$
has underlying treewidth
![]() $0$
. Now suppose
$0$
. Now suppose
![]() $H$
is a path on at most three vertices. For each
$H$
is a path on at most three vertices. For each
![]() $G\in \mathcal{I}_H$
, if
$G\in \mathcal{I}_H$
, if
![]() $G_1,\dots,G_k$
are the connected components of
$G_1,\dots,G_k$
are the connected components of
![]() $G$
, then each
$G$
, then each
![]() $G_i$
is a complete graph, implying
$G_i$
is a complete graph, implying
![]() $\{V(G_1),\dots,V(G_k)\}$
is a
$\{V(G_1),\dots,V(G_k)\}$
is a
![]() $0$
-tree-partition of
$0$
-tree-partition of
![]() $G$
with width
$G$
with width
![]() $\max _i|V(G_i)| = \textrm{tw}(G)+1$
.
$\max _i|V(G_i)| = \textrm{tw}(G)+1$
.
Lemma 45. If
![]() $H$
is a star-forest with at least one edge and at least two components, then
$H$
is a star-forest with at least one edge and at least two components, then
![]() $\mathcal{I}_H$
has underlying treewidth at least
$\mathcal{I}_H$
has underlying treewidth at least
![]() $1$
.
$1$
.
Proof. Let
![]() $G \,:\!=\, K_{2,n}$
. Then for every edge
$G \,:\!=\, K_{2,n}$
. Then for every edge
![]() $vw$
of
$vw$
of
![]() $G$
, every vertex
$G$
, every vertex
![]() $x\in V(G)\setminus \{v,w\}$
is adjacent to
$x\in V(G)\setminus \{v,w\}$
is adjacent to
![]() $v$
or
$v$
or
![]() $w$
. Thus
$w$
. Thus
![]() $G\in \mathcal{I}_H$
. Since
$G\in \mathcal{I}_H$
. Since
![]() $G$
is connected,
$G$
is connected,
![]() $\textrm{tpw}_0(G)=n+2$
. Since
$\textrm{tpw}_0(G)=n+2$
. Since
![]() $\textrm{tw}(G)\leqslant 2$
,
$\textrm{tw}(G)\leqslant 2$
,
![]() $\mathcal{I}_H$
has underlying treewidth at least
$\mathcal{I}_H$
has underlying treewidth at least
![]() $1$
.
$1$
.
Lemmas 44 and 45 prove (iv) in Theorem 38.
We finish this section with an open problem. For any set
![]() $\mathcal{X}$
of graphs, let
$\mathcal{X}$
of graphs, let
![]() $\mathcal{I}_{\mathcal{X}}$
be the class of graphs
$\mathcal{I}_{\mathcal{X}}$
be the class of graphs
![]() $G$
such that no induced subgraph of
$G$
such that no induced subgraph of
![]() $G$
is isomorphic to a graph in
$G$
is isomorphic to a graph in
![]() $\mathcal{X}$
. For which sets
$\mathcal{X}$
. For which sets
![]() $\mathcal{X}$
does
$\mathcal{X}$
does
![]() $\mathcal{I}_{\mathcal{X}}$
have bounded underlying treewidth? Consider the case when
$\mathcal{I}_{\mathcal{X}}$
have bounded underlying treewidth? Consider the case when
![]() $\mathcal{X}$
is finite. If some star-forest is in
$\mathcal{X}$
is finite. If some star-forest is in
![]() $\mathcal{X}$
, then
$\mathcal{X}$
, then
![]() $\mathcal{I}_{\mathcal{X}}$
has bounded underlying treewidth by Lemma 41. If no star-forest is in
$\mathcal{I}_{\mathcal{X}}$
has bounded underlying treewidth by Lemma 41. If no star-forest is in
![]() $\mathcal{X}$
and
$\mathcal{X}$
and
![]() $\mathcal{I}_{\mathcal{X}}$
still has bounded underlying treewidth, then some spider-forest is in
$\mathcal{I}_{\mathcal{X}}$
still has bounded underlying treewidth, then some spider-forest is in
![]() $\mathcal{X}$
(by Lemma 30), and some graph for which every component is the closure of a rooted tree is also in
$\mathcal{X}$
(by Lemma 30), and some graph for which every component is the closure of a rooted tree is also in
![]() $\mathcal{X}$
(by Corollary 14). In related work, Lozin and Razgon [Reference Lozin and Razgon54] proved a graph class defined by finitely many excluded induced subgraphs has bounded treewidth if and only if it excludes a complete graph, a complete bipartite graph, a tripod (a forest in which every connected component has at most three leaves), and the line graph of a tripod.
$\mathcal{X}$
(by Corollary 14). In related work, Lozin and Razgon [Reference Lozin and Razgon54] proved a graph class defined by finitely many excluded induced subgraphs has bounded treewidth if and only if it excludes a complete graph, a complete bipartite graph, a tripod (a forest in which every connected component has at most three leaves), and the line graph of a tripod.
9. Graph drawings
A graph is
![]() $k$
-planar if it has a drawing in the plane with at most
$k$
-planar if it has a drawing in the plane with at most
![]() $k$
crossings on each edge, where we assume that no three edges cross at the same point. Of course, the class of
$k$
crossings on each edge, where we assume that no three edges cross at the same point. Of course, the class of
![]() $0$
-planar graphs is the class of planar graphs, which has underlying treewidth
$0$
-planar graphs is the class of planar graphs, which has underlying treewidth
![]() $3$
(Theorem 21). However,
$3$
(Theorem 21). However,
![]() $1$
-planar graphs behave very differently. It is well-known that every graph has a
$1$
-planar graphs behave very differently. It is well-known that every graph has a
![]() $1$
-planar subdivision: take an arbitrary drawing of
$1$
-planar subdivision: take an arbitrary drawing of
![]() $G$
and for each edge
$G$
and for each edge
![]() $e$
add a subdivision vertex between consecutive crossings on
$e$
add a subdivision vertex between consecutive crossings on
![]() $e$
. Since the class of
$e$
. Since the class of
![]() $1$
-planar graphs is monotone, Theorem 28 implies that the class of
$1$
-planar graphs is monotone, Theorem 28 implies that the class of
![]() $1$
-planar graphs has unbounded underlying treewidth.
$1$
-planar graphs has unbounded underlying treewidth.
By restricting the type of drawing, we obtain positive results. A circular drawing of a graph
![]() $G$
positions each vertex on a circle in the plane, and draws each edge as an arc across the circle, such that no two edges cross more than once. A graph is outer
$G$
positions each vertex on a circle in the plane, and draws each edge as an arc across the circle, such that no two edges cross more than once. A graph is outer
![]() $k$
-planar if it has a circular drawing such that each edge is involved in at most
$k$
-planar if it has a circular drawing such that each edge is involved in at most
![]() $k$
crossings. The outer
$k$
crossings. The outer
![]() $0$
-planar graphs are precisely the outerplanar graphs, which have treewidth
$0$
-planar graphs are precisely the outerplanar graphs, which have treewidth
![]() $2$
. We show below that for each
$2$
. We show below that for each
![]() $k \in{\mathbb{N}}$
, the class of outer
$k \in{\mathbb{N}}$
, the class of outer
![]() $k$
-planar graphs has underlying treewidth
$k$
-planar graphs has underlying treewidth
![]() $2$
. In fact, we prove a slightly more general result. A graph is weakly outer
$2$
. In fact, we prove a slightly more general result. A graph is weakly outer
![]() $k$
-planar if it has a circular drawing such that whenever two edges
$k$
-planar if it has a circular drawing such that whenever two edges
![]() $e$
and
$e$
and
![]() $f$
cross,
$f$
cross,
![]() $e$
or
$e$
or
![]() $f$
crosses at most
$f$
crosses at most
![]() $k$
edges. Clearly every outer
$k$
edges. Clearly every outer
![]() $k$
-planar graph is weakly outer
$k$
-planar graph is weakly outer
![]() $k$
-planar.
$k$
-planar.
Theorem 46. Every weakly outer
![]() $k$
-planar graph
$k$
-planar graph
![]() $G$
has
$G$
has
![]() $2$
-tree-partition-width
$2$
-tree-partition-width
![]() $O(k^3)$
.
$O(k^3)$
.
Proof. Wood and Telle [Reference Wood and Telle80, Prop. 8.5] proved that any weakly outer
![]() $k$
-planar graph
$k$
-planar graph
![]() $G$
has
$G$
has
![]() $\textrm{tw}(G) \leqslant 3k+11$
. Thus, by Corollary 10, it suffices to show that the singleton partition of
$\textrm{tw}(G) \leqslant 3k+11$
. Thus, by Corollary 10, it suffices to show that the singleton partition of
![]() $G$
is
$G$
is
![]() $(2,4k+4)$
-disjointed. Let
$(2,4k+4)$
-disjointed. Let
![]() $v_1,\dots, v_n$
be the cyclic ordering of
$v_1,\dots, v_n$
be the cyclic ordering of
![]() $V(G)$
given by the drawing. Addition is taken modulo
$V(G)$
given by the drawing. Addition is taken modulo
![]() $n$
in this proof. If
$n$
in this proof. If
![]() $n \leqslant 2$
, then the claim holds trivially, so assume that
$n \leqslant 2$
, then the claim holds trivially, so assume that
![]() $n \geqslant 3$
. We may assume that
$n \geqslant 3$
. We may assume that
![]() $v_iv_{i+1} \in E(G)$
for all
$v_iv_{i+1} \in E(G)$
for all
![]() $i \in \{1,\dots,n\}$
.
$i \in \{1,\dots,n\}$
.
Consider distinct
![]() $v_i,v_j \in V(G)$
. If
$v_i,v_j \in V(G)$
. If
![]() $j \neq i+1$
, then let
$j \neq i+1$
, then let
![]() $v^{\prime}_r$
be the clockwise-closest vertex to
$v^{\prime}_r$
be the clockwise-closest vertex to
![]() $v_i$
that is adjacent to
$v_i$
that is adjacent to
![]() $v_j$
and let
$v_j$
and let
![]() $v^{\prime}_s$
be the anticlockwise-closest vertex to
$v^{\prime}_s$
be the anticlockwise-closest vertex to
![]() $v_i$
that is adjacent to
$v_i$
that is adjacent to
![]() $v_j$
. If
$v_j$
. If
![]() $v^{\prime}_rv_j$
is involved in more than
$v^{\prime}_rv_j$
is involved in more than
![]() $k$
crossings, then let
$k$
crossings, then let
![]() $v_r$
be the anticlockwise-closest vertex to
$v_r$
be the anticlockwise-closest vertex to
![]() $v_j$
that is incident to an edge
$v_j$
that is incident to an edge
![]() $e_r$
that crosses
$e_r$
that crosses
![]() $v^{\prime}_rv_j$
. Otherwise
$v^{\prime}_rv_j$
. Otherwise
![]() $v^{\prime}_rv_j$
is involved in at most
$v^{\prime}_rv_j$
is involved in at most
![]() $k$
crossings so let
$k$
crossings so let
![]() $v_r \,:\!=\, v^{\prime}_r$
and
$v_r \,:\!=\, v^{\prime}_r$
and
![]() $e_r \,:\!=\, v^{\prime}_rv_j$
. Similarly, if
$e_r \,:\!=\, v^{\prime}_rv_j$
. Similarly, if
![]() $v^{\prime}_sv_j$
is involved in more than
$v^{\prime}_sv_j$
is involved in more than
![]() $k$
crossings, then let
$k$
crossings, then let
![]() $v_s$
be the clockwise-closest vertex to
$v_s$
be the clockwise-closest vertex to
![]() $v_j$
that is incident to an edge
$v_j$
that is incident to an edge
![]() $e_s$
that crosses
$e_s$
that crosses
![]() $v^{\prime}_sv_j$
. Otherwise let
$v^{\prime}_sv_j$
. Otherwise let
![]() $v_s \,:\!=\, v^{\prime}_s$
and
$v_s \,:\!=\, v^{\prime}_s$
and
![]() $e_s \,:\!=\, v^{\prime}_sv_j$
. Let
$e_s \,:\!=\, v^{\prime}_sv_j$
. Let
![]() $R$
be the set of vertices that are incident to edges that cross
$R$
be the set of vertices that are incident to edges that cross
![]() $e_r$
and let
$e_r$
and let
![]() $S$
be the set of vertices incident to edges that cross
$S$
be the set of vertices incident to edges that cross
![]() $e_s$
. Let
$e_s$
. Let
![]() $Q \,:\!=\, (R \cup S \cup \{v_r,v_s,v^{\prime}_r,v^{\prime}_s\}) \setminus \{v_i,v_j\}$
. The setup so far is illustrated in Figure 5, with vertices in
$Q \,:\!=\, (R \cup S \cup \{v_r,v_s,v^{\prime}_r,v^{\prime}_s\}) \setminus \{v_i,v_j\}$
. The setup so far is illustrated in Figure 5, with vertices in
![]() $Q$
circled. We have
$Q$
circled. We have
![]() $|Q| \leqslant 4k+4$
, since
$|Q| \leqslant 4k+4$
, since
![]() $e_r$
and
$e_r$
and
![]() $e_s$
are involved in at most
$e_s$
are involved in at most
![]() $k$
crossings.
$k$
crossings.
Figure 5. Setup to define
![]() $Q$
(circled vertices) with
$Q$
(circled vertices) with
![]() $k = 2$
.
$k = 2$
.
Let
![]() $a \in N(v_i) \setminus (Q\cup \{a,b\})$
,
$a \in N(v_i) \setminus (Q\cup \{a,b\})$
,
![]() $b \in N(v_j) \setminus (Q \cup \{a,b\})$
, and
$b \in N(v_j) \setminus (Q \cup \{a,b\})$
, and
![]() $P$
be an
$P$
be an
![]() $(a,b)$
-path in
$(a,b)$
-path in
![]() $G - \{v_i,v_j\}$
. Since
$G - \{v_i,v_j\}$
. Since
![]() $G$
is weakly outer
$G$
is weakly outer
![]() $k$
-planar, if
$k$
-planar, if
![]() $P$
does not contain
$P$
does not contain
![]() $v_r$
or
$v_r$
or
![]() $v_s$
as an internal vertex, then it contains an edge that crosses
$v_s$
as an internal vertex, then it contains an edge that crosses
![]() $e_r$
or
$e_r$
or
![]() $e_s$
. Thus
$e_s$
. Thus
![]() $V(P) \cap Q \neq \varnothing$
and hence
$V(P) \cap Q \neq \varnothing$
and hence
![]() $Q$
separates
$Q$
separates
![]() $N(v_i)$
from
$N(v_i)$
from
![]() $N(v_j)$
in
$N(v_j)$
in
![]() $G - \{v_i,v_j\}$
. As such,
$G - \{v_i,v_j\}$
. As such,
![]() $G$
is
$G$
is
![]() $(2,4k+4)$
-disjointed.
$(2,4k+4)$
-disjointed.
Theorem 46 implies the next result, where the lower bound holds since
![]() $G_{2,\ell }$
from Lemma 12 is outerplanar.
$G_{2,\ell }$
from Lemma 12 is outerplanar.
Theorem 47. For every fixed
![]() $k \in{\mathbb{N}}$
, the underlying treewidth of the class of weakly outer
$k \in{\mathbb{N}}$
, the underlying treewidth of the class of weakly outer
![]() $k$
-planar graphs equals
$k$
-planar graphs equals
![]() $2$
, with constant treewidth-binding function.
$2$
, with constant treewidth-binding function.
A graph
![]() $D$
is a planarisation of a graph
$D$
is a planarisation of a graph
![]() $G$
if
$G$
if
![]() $G$
has a drawing in the plane and
$G$
has a drawing in the plane and
![]() $D$
is the graph obtained by replacing each crossing point with a dummy vertex. Observe that
$D$
is the graph obtained by replacing each crossing point with a dummy vertex. Observe that
![]() $G$
is a topological minor of
$G$
is a topological minor of
![]() $D \boxtimes K_2$
. As such, we have the following consequence of Observation 1, Lemma 27, and Theorem 21.
$D \boxtimes K_2$
. As such, we have the following consequence of Observation 1, Lemma 27, and Theorem 21.
Corollary 48. For every graph
![]() $G$
, if
$G$
, if
![]() $D$
is a planarisation of
$D$
is a planarisation of
![]() $G$
where
$G$
where
![]() $\textrm{tw}(D) \lt k$
then
$\textrm{tw}(D) \lt k$
then
![]() $G$
has
$G$
has
![]() $3$
-tree-partition-width
$3$
-tree-partition-width
![]() $O(k^{9})$
.
$O(k^{9})$
.
As a special case of Corollary 48, consider a drawing of a graph
![]() $G$
with at most
$G$
with at most
![]() $k$
crossings per edge. If
$k$
crossings per edge. If
![]() $G$
has radius
$G$
has radius
![]() $r$
, then the planarisation of
$r$
, then the planarisation of
![]() $G$
has radius at most
$G$
has radius at most
![]() $r(k+1)$
and thus has treewidth at most
$r(k+1)$
and thus has treewidth at most
![]() $3r(k+1)$
[Reference Robertson and Seymour64, (2.7)]. Thus we have the following:
$3r(k+1)$
[Reference Robertson and Seymour64, (2.7)]. Thus we have the following:
Corollary 49. If
![]() $G$
is a
$G$
is a
![]() $k$
-planar graph with radius
$k$
-planar graph with radius
![]() $r$
, then
$r$
, then
![]() $G$
has
$G$
has
![]() $3$
-tree-partition-width
$3$
-tree-partition-width
![]() $O((rk)^{9})$
.
$O((rk)^{9})$
.
Acknowledgements
This research was initiated at the Structural Graph Theory Downunder II workshop at the Mathematical Research Institute MATRIX (March 2022).