Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Aigner, Martin
and
Triesch, Eberhard
1994.
Realizability and uniqueness in graphs.
Discrete Mathematics,
Vol. 136,
Issue. 1-3,
p.
3.
Aigner, M.
and
Triesch, E.
1997.
The Mathematics of Paul Erdös II.
Vol. 14,
Issue. ,
p.
43.
Schröder, Bernd S. W.
2000.
Reconstruction of the Neighborhood Deck of an Ordered Set.
Order,
Vol. 17,
Issue. 3,
p.
255.
Fomin, Fedor V.
Kratochvíl, Jan
Lokshtanov, Daniel
Mancini, Federico
and
Telle, Jan Arne
2008.
LATIN 2008: Theoretical Informatics.
Vol. 4957,
Issue. ,
p.
194.
Boros, Endre
Gurvich, Vladimir
and
Zverovich, Igor
2008.
Neighborhood hypergraphs of bipartite graphs.
Journal of Graph Theory,
Vol. 58,
Issue. 1,
p.
69.
Gurvich, Vladimir
and
Zverovich, Igor E.
2009.
Neighborhood hypergraphs of digraphs and some matrix permutation problems.
Discrete Applied Mathematics,
Vol. 157,
Issue. 13,
p.
2836.
Fomin, Fedor V.
Kratochvíl, Jan
Lokshtanov, Daniel
Mancini, Federico
and
Telle, Jan Arne
2011.
On the complexity of reconstructing H-free graphs from their Star Systems.
Journal of Graph Theory,
Vol. 68,
Issue. 2,
p.
113.
Aigner, Martin
and
Triesch, Eberhad
2013.
The Mathematics of Paul Erdős II.
p.
5.
Köbler, Johannes
Kuhnert, Sebastian
and
Verbitsky, Oleg
2016.
Solving the canonical representation and Star System Problems for proper circular-arc graphs in logspace.
Journal of Discrete Algorithms,
Vol. 38-41,
Issue. ,
p.
38.
Kranakis, Evangelos
Krizanc, Danny
and
Lu, Yun
2016.
Algorithmic Aspects in Information and Management.
Vol. 9778,
Issue. ,
p.
150.
Lafrance, Philip
Oellermann, Ortrud R.
and
Pressey, Timothy
2017.
Reconstructing trees from digitally convex sets.
Discrete Applied Mathematics,
Vol. 216,
Issue. ,
p.
254.

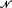 (
(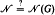 is NP-complete; for bipartite graphs the decision problem is polynomially equivalent to Graph Isomorphism; forests
is NP-complete; for bipartite graphs the decision problem is polynomially equivalent to Graph Isomorphism; forests 