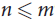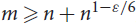Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ferber, Asaf
Sah, Ashwin
Sawhney, Mehtaab
and
Zhu, Yizhe
2023.
Sparse recovery properties of discrete random matrices.
Combinatorics, Probability and Computing,
Vol. 32,
Issue. 2,
p.
316.
Luh, Kyle
Vogel, Ryan
and
Yu, Alan
2025.
Eigenvalue gaps of random perturbations of large matrices.
Random Matrices: Theory and Applications,
Vol. 14,
Issue. 04,
Manning, Aaron
Ostafe, Alina
and
Shparlinski, Igor E.
2026.
Counting matrices over finite rank multiplicative groups.
Pacific Journal of Mathematics,
Vol. 340,
Issue. 1,
p.
115.