Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-11T04:20:52.391Z Has data issue: false hasContentIssue false
  • English
  • Français

Set Systems Containing Many Maximal Chains

Published online by Cambridge University Press:  09 October 2014

J. ROBERT JOHNSON ,
IMRE LEADER  and
PAUL A. RUSSELL
J. ROBERT JOHNSON
Affiliation:
School of Mathematical Sciences, Queen Mary, University of London, London E1 4NS, UK (e-mail: r.johnson@qmul.ac.uk)
IMRE LEADER
Affiliation:
Department of Pure Mathematics and Mathematical Statistics, Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WB, UK (e-mail: i.leader@dpmms.cam.ac.uk, p.a.russell@dpmms.cam.ac.uk)
PAUL A. RUSSELL
Affiliation:
Department of Pure Mathematics and Mathematical Statistics, Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WB, UK (e-mail: i.leader@dpmms.cam.ac.uk, p.a.russell@dpmms.cam.ac.uk)
Get access Rights & Permissions [Opens in a new window]

Abstract

The purpose of this short problem paper is to raise the following extremal question on set systems: Which set systems of a given size maximise the number of (n + 1)-element chains in the power set 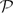$\mathcal{P}$(1,2,. . .,n)? We will show that for each fixed α > 0 there is a family of α2n sets containing (α + o(1))n! such chains, and that this is asymptotically best possible. For smaller set systems we conjecture that a ‘tower of cubes’ construction is extremal. We finish by mentioning briefly a connection to an extremal problem on posets and a variant of our question for the grid graph.

Keywords

Primary 05D05
Type
Problem Papers
Information
Combinatorics, Probability and Computing , Volume 24 , Issue 3 , May 2015 , pp. 480 - 485
Copyright
Copyright © Cambridge University Press 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Alon, N. and Frankl, P. (1985) The maximum number of disjoint pairs in a family of subsets. Graphs Combin. 1 13–21.Google Scholar
[2]Bollobás, B. (1986) Combinatorics, Cambridge University Press.Google Scholar
[3]Das, S., Gan, W. and Sudakov, B. Sperner's theorem and a problem of Erdős, Katona and Kleitman. Combin. Probab. Comput., to appear.Google Scholar
[4]Dove, A. P., Griggs, J. R., Kang, R. J. and Sereni, J.-S. (2014) Supersaturation in the Boolean lattice. Integers 14A, Paper No. A4Google Scholar
[5]Katona, G. O. H., Katona, G. Y. and Katona, Z. (2012) Most probably intersecting families of subsets. Combin. Probab. Comput. 21 219–227.Google Scholar
[6]Kleitman, D. (1968) A conjecture of Erdős–Katona on commensurable pairs of subsets of an n-set. In Theory of Graphs: Proc. Colloquium Held at Tihany, Hungary, September 1966 (Erdős, P. and Katona, G., eds), Academic Press, pp. 215–218.Google Scholar
[7]Russell, P. A. (2012) Compressions and probably intersecting families. Combin. Probab. Comput. 21 301–313.Google Scholar