Article contents
Sharp concentration of the equitable chromatic number of dense random graphs
Published online by Cambridge University Press: 26 November 2019
Abstract
An equitable colouring of a graph G is a vertex colouring where no two adjacent vertices are coloured the same and, additionally, the colour class sizes differ by at most 1. The equitable chromatic number χ=(G) is the minimum number of colours required for this. We study the equitable chromatic number of the dense random graph 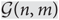 ${\mathcal{G}(n,m)}$ where
${\mathcal{G}(n,m)}$ where 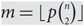 $m = \left\lfloor {p\left( \matrix{n \cr 2 \cr}\right)} \right\rfloor $ and 0 < p < 0.86 is constant. It is a well-known question of Bollobás [3] whether for p = 1/2 there is a function f(n) → ∞ such that, for any sequence of intervals of length f(n), the normal chromatic number of
$m = \left\lfloor {p\left( \matrix{n \cr 2 \cr}\right)} \right\rfloor $ and 0 < p < 0.86 is constant. It is a well-known question of Bollobás [3] whether for p = 1/2 there is a function f(n) → ∞ such that, for any sequence of intervals of length f(n), the normal chromatic number of 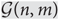 ${\mathcal{G}(n,m)}$ lies outside the intervals with probability at least 1/2 if n is large enough. Bollobás proposes that this is likely to hold for f(n) = log n. We show that for the equitable chromatic number, the answer to the analogous question is negative. In fact, there is a subsequence
${\mathcal{G}(n,m)}$ lies outside the intervals with probability at least 1/2 if n is large enough. Bollobás proposes that this is likely to hold for f(n) = log n. We show that for the equitable chromatic number, the answer to the analogous question is negative. In fact, there is a subsequence 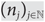 ${({n_j})_j}_{ \in {\mathbb {N}}}$ of the integers where
${({n_j})_j}_{ \in {\mathbb {N}}}$ of the integers where 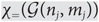 $\chi_=({\mathcal{G}(n_j,m_j)})$ is concentrated on exactly one explicitly known value. This constitutes surprisingly narrow concentration since in this range the equitable chromatic number, like the normal chromatic number, is rather large in absolute value, namely asymptotically equal to n/(2logbn) where b = 1/(1 − p).
$\chi_=({\mathcal{G}(n_j,m_j)})$ is concentrated on exactly one explicitly known value. This constitutes surprisingly narrow concentration since in this range the equitable chromatic number, like the normal chromatic number, is rather large in absolute value, namely asymptotically equal to n/(2logbn) where b = 1/(1 − p).
MSC classification
Information
- Type
- Paper
- Information
- Copyright
- © Cambridge University Press 2019
Footnotes
This research was partially funded by ERC grant 676632.
References
- 3
- Cited by

