Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-13T07:00:26.835Z Has data issue: false hasContentIssue false
  • English
  • Français

A simplified disproof of Beck’s three permutations conjecture and an application to root-mean-squared discrepancy

Part of: Discrete mathematics in relation to computer science Extremal combinatorics

Published online by Cambridge University Press:  26 October 2020

Cole Franks
Cole Franks*
Affiliation:
Department of Mathematics, Rutgers University, Piscataway, NJ08854, USA Email: franks@mit.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

A k-permutation family on n vertices is a set-system consisting of the intervals of k permutations of the integers 1 to n. The discrepancy of a set-system is the minimum over all red–blue vertex colourings of the maximum difference between the number of red and blue vertices in any set in the system. In 2011, Newman and Nikolov disproved a conjecture of Beck that the discrepancy of any 3-permutation family is at most a constant independent of n. Here we give a simpler proof that Newman and Nikolov’s sequence of 3-permutation families has discrepancy 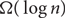$\Omega (\log \,n)$. We also exhibit a sequence of 6-permutation families with root-mean-squared discrepancy 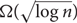$\Omega (\sqrt {\log \,n} )$; that is, in any red–blue vertex colouring, the square root of the expected squared difference between the number of red and blue vertices in an interval of the system is 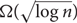$\Omega (\sqrt {\log \,n} )$.

MSC classification

Primary: 68R01: General
Secondary: 05D99: None of the above, but in this section
Type
Paper
Information
Combinatorics, Probability and Computing , Volume 30 , Issue 3 , May 2021 , pp. 398 - 411
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

†

Supported in part by Simons Foundation award 332622.

References

Erdős, P. and Moon, J. (1965) On sets of consistent arcs in a tournament. Canad. Math. Bull. 8 269–271.CrossRefGoogle Scholar
Guruswami, V., Manokaran, R. and Raghavendra, P. (2008) Beating the random ordering is hard: inapproximability of maximum acyclic subgraph. In IEEE 49th Annual Symposium on Foundations of Computer Science (FOCS ’08), pp. 573–582. IEEE.Google Scholar
Larsen, K. G. (2019) Constructive discrepancy minimization with hereditary L2 guarantees. In 36th International Symposium on Theoretical Aspects of Computer Science (STACS 2019). Schloss Dagstuhl-Leibniz-Zentrum fuer Informatik.Google Scholar
Lovász, L., Spencer, J. and Vesztergombi, K. (1986) Discrepancy of set-systems and matrices. European J. Combin. 7 151–160.CrossRefGoogle Scholar
Matoušek, J. (2013) The determinant bound for discrepancy is almost tight. Proc. Amer. Math. Soc. 141 451–460.Google Scholar
Newman, A., Neiman, O. and Nikolov, A. (2012) Beck’s three permutations conjecture: a counterexample and some consequences. In IEEE 53rd Annual Symposium on Foundations of Computer Science (FOCS), pp. 253–262. IEEE.Google Scholar
Newman, A. and Nikolov, A. (2011) A counterexample to Beck’s conjecture on the discrepancy of three permutations. arXiv:1104.2922Google Scholar
Nikolov, A., Talwar, K. and Zhang, L. (2013) The geometry of differential privacy: the sparse and approximate cases. In 45th Annual ACM Symposium on Theory of Computing (STOC ’13), pp. 351–360. ACM.CrossRefGoogle Scholar
Spencer, J. H. (1987) Ten Lectures on the Probabilistic Method, Vol. 52 of Proc. CBMS-NRM Regional Conference Series in Applied Mathematics. SIAM.Google Scholar
Spencer, J. H., Srinivasan, A. and Tetali, P. (2018) The discrepancy of permutation families.Google Scholar