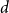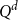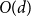Supercritical site percolation on the hypercube: small components are small

Abstract

We consider supercritical site percolation on the $d$ -dimensional hypercube $Q^d$ . We show that typically all components in the percolated hypercube, besides the giant, are of size $O(d)$ . This resolves a conjecture of Bollobás, Kohayakawa, and Łuczak from 1994.

1. Introduction

The $d$ -dimensional hypercube $Q^d$ is the graph with the vertex set $V\big(Q^d\big)=\{0,1\}^d$ , where two vertices are adjacent if they differ in exactly one coordinate. Throughout this paper, we denote by $n=2^d$ the order of the hypercube.

In bond percolation on $G$ , one considers the subgraph $G_p$ obtained by including every edge independently with probability $p$ . Erdős and Spencer [1] conjectured that, similar to the classical $G(n,p)$ model, there is a phase transition at $p=\frac{1}{d}$ in $Q^d_p$ : for $\epsilon \gt 0$ , when $p=\frac{1-\epsilon }{d}$ , whp all components have size $O(d)$ , and when $p=\frac{1+\epsilon }{d}$ , there exists whp a unique giant component in $Q^d_p$ whose order is linear in $n$ . Their conjecture was proved by Ajtai, Komlós, and Szemerédi [2]. Bollobás, Kohayakawa, and Łuczak [3] improved upon that result, extending it to a wider range of $p$ , allowing $\epsilon =o(1)$ , and giving an asymptotic value of the order of the giant component of $Q^d_p$ . Furthermore, they proved that the second largest component in $Q^d_p$ is typically of order $O(d)$ .

In site percolation on $G$ , one considers the induced subgraph $G[R]$ , where $R$ is a random subset of vertices formed by including each vertex independently with probability $p$ . In the setting of site percolation on the hypercube, Bollobás, Kohayakawa, and Łuczak [4] proved the following:

Theorem 1.1. (Theorems 8, 9 of [4]) Let $\epsilon \gt 0$ be a small enough constant, and let $p=\frac{1+\epsilon }{d}$ . Let $R$ be a random subset formed by including each vertex of $Q^d$ independently with probability $p$ . Then, whp , there is a unique giant component of $Q^d[R]$ , whose asymptotic size is $\frac{\left (2\epsilon -O\left(\epsilon ^2\right)\right )n}{d}$ . Furthermore, whp the size of the other components is at most $d^{10}$ .

Motivated by the results in bond percolation on the hypercube, in the same paper [4], and also in their paper on bond percolation on the hypercube [3], Bollobás, Kohayakawa, and Łuczak conjectured that whp all the components of $Q^d[R]$ besides the giant component are of asymptotic size at most $\gamma d$ , where $\gamma$ is a constant depending only on $\epsilon$ (see Conjecture 11 of [4]). We prove this conjecture:

Theorem 1.2. Let $\epsilon \gt 0$ be a small enough constant, and let $p=\frac{1+\epsilon }{d}$ . Let $R$ be a random subset formed by including each vertex of $Q^d$ independently with probability $p$ . Then, whp , all the components of $Q^d[R]$ besides the giant component are of size $O_{\epsilon}(d )$ .

We note that in our proof we obtain an inverse polynomial dependency on $\epsilon$ , of order $\frac{1}{\epsilon ^5}$ , in the hidden constant in $O_{\epsilon }(d)$ .

The text is structured as follows. In Section 2, we show that big components are ‘everywhere dense’ (see the exact definition in Lemma 2.3). In Section 3, we exhibit several structures that whp do not appear in the site-percolated hypercube. In Section 4, we prove Theorem 1.2.

Our notation is fairly standard. Throughout the rest of the text, unless specifically stated otherwise, we set $\epsilon$ to be a small enough constant, $p=\frac{1+\epsilon }{d}$ , and $R$ to be a random subset of $V\big(Q^d\big)$ formed by including each vertex independently with probability $p$ . Furthermore, we denote by $L_1$ the largest connected component of $Q^d[R]$ . We denote by $N_G(S)$ the external neighbourhood of a set $S$ in the graph $G$ . When $T$ is a subset of $V(G)$ , we write $N_T(S)=N_G(S)\cap T$ . We omit rounding signs for the sake of clarity of presentation.

2. Big components are everywhere dense

We begin with the following claim, which holds for any $d$ -regular graph:

Claim 2.1. Let $G=(V,E)$ be a $d$ -regular graph on $n$ vertices. Let $\epsilon$ be a small enough constant, and let $p=\frac{1+\epsilon }{d}$ . Form $R\subseteq V$ by including each vertex of $V$ independently with probability $p$ . Then, whp , any connected component $S$ of $G[R]$ with $|S|=k\gt 300\ln n$ has $|N_G(S)|\ge \frac{9kd}{10}$ .

Proof. We run the depth first search (DFS) algorithm with $n$ random bits $X_i$ , discovering the connected components while generating $G[R]$ (see [5]). If there is a connected component $S$ of size $k$ , then there is an interval of random bits whose length is $k+|N_G(S)|$ in the DFS where we receive $k$ positive answers. Thus, the probability of having a component violating the claim, whose discovery by the DFS starts with a given bit $X_i$ is at most:

\begin{align*} \mathbb{P}\!\left [Bin\!\left (\frac{9kd}{10}+k,\frac{1+\epsilon }{d}\right )\ge k\right ] \end{align*}

Hence, by a Chernoff-type bound (see Appendix A in [6]), the probability of having such a component is at most

\begin{align*} \exp \!\left (-\frac{k}{100}\right )\le o\!\left (\frac{1}{n^2}\right ), \end{align*}

where the inequality follows from our bound on $k$ . We complete the proof with a union bound on the $\lt n$ possible values of $k$ and $\lt n$ possible starting points of the interval in the DFS.

We further require the following simple claim:

Claim 2.2. Let $S\subseteq V\big(Q^d\big)$ such that $|S|=k\le d$ . Then, there exist pairwise disjoint subcubes, each of dimension at least $d-k+1$ , such that every $v\in S$ is in exactly one of these subcubes.

Proof. We prove by induction on $k$ . The case $k=1$ is trivial.

Assume that the statement holds for all $k^{\prime}\lt k$ . Choose any two vertices of $S$ . There is at least one coordinate on which they do not agree. Consider the two pairwise disjoint (and complementary) subcubes of dimension $d-1$ : one where we fix this coordinate to be $0$ and let the other coordinates vary, and the other where we fix this coordinate to be $1$ and let the other coordinates vary. Clearly, each of the two vertices is in exactly one of these subcubes. Since these subcubes are disjoint, no vertex from the other $k-2$ vertices is in both of them. We can then apply the induction hypothesis on each of these subcubes, giving rise to pairwise disjoint subcubes of dimension at least $d-1-(k-2)=d-k+1$ , each having exactly one of the vertices of $S$ .

We conclude this section with a lemma, bounding the probability that a fixed small set of vertices has no vertex at Hamming distance $1$ from many vertices in large components or in their neighbourhoods. The proof here borrows several ideas used in [2, 4, 7].

Lemma 2.3. Fix $S\subseteq V\big(Q^d\big)$ of cardinality $|S|=k\le \frac{\epsilon d}{10}$ . Let $X$ be the set of vertices in components of $Q^d[R]$ of order at least $n^{1-\epsilon }$ . Then, the probability that every $v\in S$ has less than $\frac{\epsilon ^2d}{40}$ neighbours (in $Q^d$ ) in $X\cup N_{Q^d}(X)$ is at most $\exp \!\left (-\frac{\epsilon ^2dk}{40}\right )$ .

Proof. Let $S=\{v_1,\cdots, v_k\}$ . By Claim 2.2, we can consider pairwise disjoint subcubes of dimension at least $\left (1-\frac{\epsilon }{10}\right )d$ , each containing exactly one of the vertices of $S$ . We denote these subcubes by $Q_1,\cdots, Q_k$ , where $v_i\in V(Q_i)$ .

For each $i$ , consider $Q_i$ , and assume, without loss of generality, that $v_i$ is the origin of $Q_i$ . We then create $\frac{\epsilon d}{10}$ pairwise disjoint subcubes of $Q_i$ of dimension at least $\left (1-\frac{\epsilon }{5}\right )d$ , each at distance $1$ from $v_i$ , by fixing one of the first $\frac{\epsilon d}{10}$ coordinates of $Q_i$ to be $1$ , the rest of the first $\frac{\epsilon d}{10}$ coordinates to be $0$ , and letting the other coordinates vary. Denote these subcubes by $Q_i(1), \cdots, Q_i\!\left (\frac{\epsilon d}{10}\right )$ , and the vertex at distance $1$ from $v_i$ in $Q_i(j)$ by $v_i(j)$ . We denote by $n^{\prime}$ the order of each $Q_i(j)$ , and note that $n^{\prime}\ge 2^{\left (1-\frac{\epsilon }{5}\right )d}=n^{1-\frac{\epsilon }{5}}$ .

Fix $i$ . Observe that $p$ is still supercritical at every $Q_i(j)$ since $(1+\epsilon )\left (1-\frac{\epsilon }{5}\right )\ge 1+\frac{3\epsilon }{5}$ . Denote by $L_1(i,j)$ the largest component of $Q_i(j)[R]$ . Then, by Theorem 1.1, whp $\big |L_1(i,j)\big |\ge \frac{7\epsilon n^{\prime}}{6d}.$ Furthermore, by Claim 2.1, whp $\big|N_{Q_i(j)}\left (L_1(i,j)\right )\big|\ge \frac{21\epsilon n^{\prime}}{20}.$ Thus, setting $\mathcal{A}_{(i,j)}$ to be the event that $\big|L_1(i,j)\cup N_{Q_i(j)}\!\left (L_1(i,j)\right )\big|\ge \frac{21\epsilon n^{\prime}}{20}$ , we have that $P (\mathcal{A}_{(i,j)} )=1-o(1)$ . Now, let $\mathcal{B}_{(i,j)}$ be the event that $v_i(j)\in L_1(i,j)\cup N_{Q_i(j)} (L_1(i,j) )$ . Since the hypercube is transitive, we have that $P\!\left (\mathcal{B}_{(i,j)}|\mathcal{A}_{(i,j)}\right )\ge \frac{21\epsilon n^{\prime}/20}{n^{\prime}}=\frac{21\epsilon }{20}$ . Therefore, $P\!\left (\mathcal{B}_{(i,j)}\cap \mathcal{A}_{(i,j)}\right )\ge \left (1-o(1)\right )\frac{21 \epsilon }{20}\ge \epsilon$ . Since the subcubes $Q_i(j)$ are pairwise disjoint, the events $B_{(i,j)}\cap \mathcal{A}_{(i,j)}$ are independent for different $j$ . Thus, by a typical Chernoff-type bound, with probability at least $1-\exp \!\left (-\frac{\epsilon ^2d}{40}\right )$ , at least $\frac{\epsilon ^2d}{40}$ of the $v_i(j)$ are in $L_1(i,j)\cup N_{Q_i(j)} (L_1(i,j) )$ with $\big|L_1(i,j)\cup N_{Q_i(j)}\!\left (L_1(i,j)\right )\big|\ge \frac{21\epsilon n^{\prime}}{20}$ . Thus, with the same probability, $v_i$ is at distance $1$ from at least $\frac{\epsilon ^2d}{40}$ vertices in components whose size is at least $\frac{\epsilon n^{\prime}}{d}\ge \frac{\epsilon n^{1-\frac{\epsilon }{5}}}{d}\ge n^{1-\epsilon }$ or in their neighbourhoods, that is, in $X\cup N_{Q^d}(X)$ .

Since $v_i$ ’s are in pairwise disjoint subcubes, these events are also independent for each $v_i$ . Hence, the probability that none of the $v_i$ are at distance $1$ from at least $\frac{\epsilon ^2d}{40}$ vertices in $X\cup N_{Q^d}(X)$ is at most $\exp \!\left (-\frac{\epsilon ^2dk}{40}\right )$ .

3. Unlikely structures in the percolated hypercube

Denote by $N^2_G(v)$ the set of vertices in $G$ at distance exactly $2$ from $v$ . The following lemma shows that, typically, there are no large sections of a sphere of radius $2$ in $Q^d[R]$ .

Lemma 3.1. Whp , there is no $v\in Q^d$ such that $ \big|N^2_{Q^d}(v)\cap R \big|\ge 2d$ .

Proof. We have $n$ ways to choose $v$ , and $\displaystyle\binom{\binom{d}{2}}{2d}$ ways to choose a subset of $2d$ vertices from $N^2_{Q^d}(v)$ . We include them in $R$ with probability $p^{2d}$ . Hence, by the union bound, the probability of violating the lemma is at most:

\begin{align*} 2^d\binom{\binom{d}{2}}{2d}\left (\frac{1+\epsilon }{d}\right )^{2d}\le 2^d\!\left (\frac{ed}{4}\cdot \frac{1+\epsilon }{d}\right )^{2d}\le \left (\frac{14}{15}\right )^{d}=o(1). \end{align*}

From Lemma 3.1, we are able to derive the following lemma:

Lemma 3.2. Whp there are no $S\subseteq R$ and $W\subseteq V\big(Q^d\big)$ disjoint from $S$ such that $|W|\le \frac{\epsilon ^4d|S|}{9\cdot 200^2}$ and every $v\in S$ has $d_{Q^d}(v, W)\ge \frac{\epsilon ^2d}{200}$ .

Proof. Assume the contrary. By our assumption on $S$ , there are at least $\frac{\epsilon ^2 d|S|}{200}$ edges between $S$ and $W$ . Thus, the average degree from $W$ to $S$ is at least $\frac{\epsilon ^2 d|S|}{200|W|}$ . Now, let us count the number of cherries with the vertex of degree $2$ in $W$ . By Jensen’s inequality, we have at least $\binom{\epsilon ^2 d|S|/200|W|}{2}|W|\ge \frac{\epsilon ^4d^2|S|^2}{4\cdot 200^2|W|}\ge \frac{9d|S|}{4}$ such cherries, where we used our assumption on $|W|$ . Thus, by the pigeonhole principle, there is a vertex $v\in S$ that is in $\frac{2}{|S|}\cdot \frac{9d|S|}{4}=\frac{9d}{2}$ cherries. Since every pair of vertices in $S$ is connected by at most two paths of length $2$ in $Q^d$ , we obtain that $v$ is at Hamming distance $2$ from at least $\frac{\frac{9d}{2}}{2}=\frac{9d}{4}\gt 2d$ vertices in $S\subseteq R$ . On the other hand, by Lemma 3.1, whp there is no $v\in Q^d$ such that $|N_{Q^d}^2(v)\cap R|\ge 2d$ , completing the proof.

The next lemma bounds the number of subtrees of a given order in a $d$ -regular graph.

Lemma 3.3. Let $t_k(G)$ denote the number of $k$ -vertex trees contained in a $d$ -regular graph $G$ on $n$ vertices. Then,

\begin{equation*}t_k(G)\le n(ed)^{k-1}.\end{equation*}

This follows directly from Lemma 2.1 of [8].

We are now ready to state and prove the final lemma of this section:

Lemma 3.4. Let $C\gt 0$ be a constant, and let $\delta \gt 0$ be a small enough constant. Let $q=\frac{1+\delta }{d}$ , and form $R_q$ by including each vertex $v\in V\big(Q^d\big)$ independently with probability $q$ . Let $L_1$ the largest component of $Q^d[R_q]$ . Then, whp , there is no $S\subseteq V\big(Q^d\big)$ , such that $|S|=Cd$ , $S$ is connected in $Q^d$ , and at least $\frac{\delta d}{10}$ vertices $v\in S$ have that $\big |N_{L_1\cup N_{Q^d}(L_1)}(v)\big |\lt \frac{\delta ^2d}{40}$ .

Proof. By Theorem 1.1, whp there is a unique giant component whose size is larger than $d^{10}$ , which we denote by $L_1$ . Thus, it suffices to show that whp there is no such $S$ , where $\frac{\delta d}{10}$ of its vertices have less than $\frac{\delta ^2d}{40}$ vertices at Hamming distance $1$ from components of size at least $n^{1-\delta }$ or their neighbourhoods, since whp these components and their neighbourhoods are in fact $L_1\cup N_{Q^d}(L_1)$ .

By Lemma 3.3, we have $n(ed)^{Cd}$ ways to choose $S$ . We have $\displaystyle\binom{Cd}{\frac{\delta d}{10}}$ ways to choose the vertices in $S$ which do not have at least $\frac{\delta ^2d}{40}$ vertices at Hamming distance $1$ from components of size at least $n^{1-\delta }$ or their neighbourhoods. By Lemma 2.3, the probability that no vertex in a given set of $\frac{\delta d}{10}$ vertices in $S$ has at least $\frac{\delta ^2d}{40}$ vertices at Hamming distance $1$ from components of size at least $n^{1-\delta }$ or their neighbourhoods is at most $\exp \!\left (-\frac{\delta ^4d^2}{400}\right )$ . Hence, the probability of the event violating the statement of the lemma is at most:

\begin{align*} n(ed)^{Cd}\binom{Cd}{\frac{\delta d}{10}}\exp \!\left (-\frac{\delta ^4d^2}{400}\right )\le n\!\left ((ed)^C\!\left (\frac{10eC}{\delta }\right )^{\frac{\delta }{10}}\exp \!\left (-\frac{\delta ^4d}{400}\right )\right )^d=o(1). \end{align*}

4. Proof of Theorem 1.2

Let $p_1=\frac{1+\epsilon/2}{d}$ . Form $R_1$ by including each vertex $v\in V\big(Q^d\big)$ independently with probability $p_1$ . By Theorem 1.1, whp there is a unique giant component, denote it by $L^{\prime}_1$ . We can thus split the vertices of the hypercube into the following three disjoint sets: $T=L^{\prime}_1\cup N_{Q^d}\!\left(L^{\prime}_1\right)$ , $M$ is the set of vertices outside $T$ with at least $\frac{\epsilon ^2d}{200}$ neighbours in $T$ , and $S=V \big(Q^d\big)\setminus (T\cup M )$ .

Let $p_2=\frac{\epsilon }{2d-2-\epsilon }$ . Form $R_2$ by including each vertex $v\in V\big(Q^d\big)$ independently with probability $p_2$ . Note that since $1-p=(1-p_1)(1-p_2)$ , the random set $R$ has the same distribution as $R_1\cup R_2$ . Thus, with a slight abuse of notation, we write $R=R_1\cup R_2$ . We now perform the second exposure (that is, generate $R_2$ ) on $S\cup M$ first, and only afterwards on $T$ . Note that once we show that a connected set (that is, a connected subset of $Q^d [(S\cup M)\cap R_2 ]$ ) has a neighbour in $T\cap R_2$ , it means that it merges into $L^{\prime}_1$ (whereas by Theorem 1.1, whp $L^{\prime}_1\subseteq L_1$ ). Furthermore, note that all the components of $Q^d[R]$ outside $L_1$ are subsets of $S\cup M$ .

We will now show that whp there are no components contained in $(S\cup M)\cap R$ of size at least $2C_1d$ for an appropriate choice of a constant $C_1\gt 0$ , possibly depending $\epsilon$ . We first consider the case where this connected component $B$ has at least $C_1d$ vertices in $M$ , and show that in that case, whp $B$ merges with $L^{\prime}_1$ after the second exposure on $T$ . By construction, every $v\in M$ has at least $\frac{\epsilon ^2d}{200}$ neighbours in $T$ , and $T\cap M=\emptyset$ . Thus, by Lemma 3.2, we have that whp $\big |N_T(B\cap M)\big |\ge \frac{C_1\epsilon ^4d^2}{9\cdot 200^2}$ . Hence,

\begin{align*} \mathbb{P}\!\left [\big |N_T(B)\cap R_2\big |=0\right ]&\le \left (1-\frac{\epsilon }{2d}\right )^{\frac{C_1\epsilon ^4d^2}{9\cdot 200^2}}\le \exp \!\left (-\frac{C_1\epsilon ^5d}{18\cdot 200^2}\right )=o(1/n), \end{align*}

by choosing $C_1\ge \frac{18\cdot 200^2}{\epsilon ^5}$ . We conclude with the union bound over the $\lt n$ connected components in $(S\cup M)\cap R$ .

Thus, we are left to deal with connected components $B\subseteq (S\cup M)\cap R$ of size at least $2C_1d$ with less than $C_1d$ vertices in $B\cap M$ . Taking a connected subset $B^{\prime}\subseteq B$ of size exactly $Cd\,:\!=\,2C_1d$ , we have that $|B^{\prime}\cap S|\ge |B^{\prime}|-|B^{\prime}\cap M|\ge C_1d\ge \frac{\epsilon d}{20}$ . Recalling that $S, M,T$ and $L^{\prime}_1$ were formed according to the supercritical percolation with $p_1=\frac{1+\epsilon/2}{d}$ , by Lemma 3.4 applied with $\delta =\frac{\epsilon }{2}$ , whp there is no connected set of size $Cd$ in $Q^d$ with at least $\frac{\frac{\epsilon }{2} d}{10}=\frac{\epsilon d}{20}$ vertices which do not have at least $\frac{\left (\frac{\epsilon }{2}\right )^2d}{40}\gt \frac{\epsilon ^2d}{200}$ vertices at Hamming distance $1$ from $L^{\prime}_1\cup N_{Q^d}\!\left(L^{\prime}_1\right)$ . Thus, whp there is no such connected set $B^{\prime}$ . All in all, whp, there is no connected component $B$ in $Q^d[R]$ of size at least $Cd$ outside of $L_1$ .