Article contents
Tight Hamilton cycles in cherry-quasirandom 3-uniform hypergraphs
Published online by Cambridge University Press: 12 October 2020
Abstract
We employ the absorbing-path method in order to prove two results regarding the emergence of tight Hamilton cycles in the so-called two-path or cherry-quasirandom 3-graphs.
Our first result asserts that for any fixed real α > 0, cherry-quasirandom 3-graphs of sufficiently large order n having minimum 2-degree at least α(n – 2) have a tight Hamilton cycle.
Our second result concerns the minimum 1-degree sufficient for such 3-graphs to have a tight Hamilton cycle. Roughly speaking, we prove that for every d, α > 0 satisfying d + α > 1, any sufficiently large n-vertex such 3-graph H of density d and minimum 1-degree at least 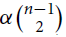 $\alpha \left({\matrix{{n - 1} \cr 2 \cr } } \right)$ has a tight Hamilton cycle.
$\alpha \left({\matrix{{n - 1} \cr 2 \cr } } \right)$ has a tight Hamilton cycle.
MSC classification
Information
- Type
- Paper
- Information
- Creative Commons
- This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
- 4
- Cited by


