Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bollob�s, B�la
and
Thomason, Andrew
1996.
Highly linked graphs.
Combinatorica,
Vol. 16,
Issue. 3,
p.
313.
Komlós, János
and
Szemerédi, Endre
1996.
Topological cliques in graphs II.
Combinatorics, Probability and Computing,
Vol. 5,
Issue. 1,
p.
79.
Simonovits, Miklós
1997.
The Mathematics of Paul Erdös II.
Vol. 14,
Issue. ,
p.
148.
Balbuena, C.
Cera, M.
Diánez, A.
and
García-Vázquez, P.
2007.
New exact values of the maximum size of graphs free of topological complete subgraphs.
Discrete Mathematics,
Vol. 307,
Issue. 9-10,
p.
1038.
Nešetřil, Jaroslav
and
Ossona de Mendez, Patrice
2011.
On nowhere dense graphs.
European Journal of Combinatorics,
Vol. 32,
Issue. 4,
p.
600.
Füredi, Zoltán
and
Simonovits, Miklós
2013.
Erdős Centennial.
Vol. 25,
Issue. ,
p.
169.
Stein, Maya
and
Zamora, José
2013.
Forcing Large Complete (Topological) Minors in Infinite Graphs.
SIAM Journal on Discrete Mathematics,
Vol. 27,
Issue. 2,
p.
697.
Balogh, József
Liu, Hong
and
Sharifzadeh, Maryam
2015.
Subdivisions of a large clique in C6-free graphs.
Journal of Combinatorial Theory, Series B,
Vol. 112,
Issue. ,
p.
18.
Montgomery, Richard
2015.
Logarithmically small minors and topological minors.
Journal of the London Mathematical Society,
Vol. 91,
Issue. 1,
p.
71.
Kim, Jaehoon
Liu, Hong
Sharifzadeh, Maryam
and
Staden, Katherine
2017.
Proof of Komlós's conjecture on Hamiltonian subsets.
Electronic Notes in Discrete Mathematics,
Vol. 61,
Issue. ,
p.
727.
Kim, Jaehoon
Liu, Hong
Sharifzadeh, Maryam
and
Staden, Katherine
2017.
Proof of Komlós's conjecture on Hamiltonian subsets.
Proceedings of the London Mathematical Society,
Vol. 115,
Issue. 5,
p.
974.
Liu, Hong
and
Montgomery, Richard
2017.
A proof of Mader's conjecture on large clique subdivisions in C4-free graphs.
Journal of the London Mathematical Society,
Vol. 95,
Issue. 1,
p.
203.
Krivelevich, Michael
2018.
Finding and Using Expanders in Locally Sparse Graphs.
SIAM Journal on Discrete Mathematics,
Vol. 32,
Issue. 1,
p.
611.
Haslegrave, John
Kim, Jaehoon
and
Liu, Hong
2021.
Extended Abstracts EuroComb 2021.
Vol. 14,
Issue. ,
p.
25.
Haslegrave, John
Kim, Jaehoon
and
Liu, Hong
2022.
Extremal density for sparse minors and subdivisions.
International Mathematics Research Notices,
Vol. 2022,
Issue. 20,
p.
15505.
Haslegrave, John
Hu, Jie
Kim, Jaehoon
Liu, Hong
Luan, Bingyu
and
Wang, Guanghui
2022.
Crux and Long Cycles in Graphs.
SIAM Journal on Discrete Mathematics,
Vol. 36,
Issue. 4,
p.
2942.
Bucić, Matija
and
Montgomery, Richard
2023.
Towards the Erdős-Gallai Cycle Decomposition Conjecture.
p.
839.
Im, Seonghyuk
Kim, Jaehoon
Kim, Younjin
and
Liu, Hong
2023.
Crux, space constraints and subdivisions.
p.
607.
Wang, Yan
2023.
Balanced Subdivisions of a Large Clique in Graphs with High Average Degree.
SIAM Journal on Discrete Mathematics,
Vol. 37,
Issue. 2,
p.
1262.
Liu, Hong
and
Montgomery, Richard
2023.
A solution to Erdős and Hajnal’s odd cycle problem.
Journal of the American Mathematical Society,

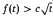 . Here we prove the weaker estimate
. Here we prove the weaker estimate  .
.