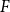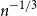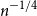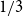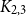1. Introduction
Given a family
![]() $\mathcal{F}$
of graphs we say a graph
$\mathcal{F}$
of graphs we say a graph
![]() $G$
is
$G$
is
![]() $\mathcal{F}$
-free if it does not contain any member in
$\mathcal{F}$
-free if it does not contain any member in
![]() $\mathcal{F}$
as a subgraph. A fundamental problem in extremal graph theory is to determine the maximum number
$\mathcal{F}$
as a subgraph. A fundamental problem in extremal graph theory is to determine the maximum number
![]() $\mathrm{ex}(n, \mathcal{F})$
of edges in an
$\mathrm{ex}(n, \mathcal{F})$
of edges in an
![]() $\mathcal{F}$
-free graph on
$\mathcal{F}$
-free graph on
![]() $n$
vertices. Here
$n$
vertices. Here
![]() $\mathrm{ex}(n, \mathcal{F})$
is called the Turán number of
$\mathrm{ex}(n, \mathcal{F})$
is called the Turán number of
![]() $\mathcal{F}$
, and the limit
$\mathcal{F}$
, and the limit
![]() $\pi (F) = \lim _{n\to \infty } \mathrm{ex}(n, \mathcal{F})/\binom{n}{2}$
, whose existence was proved by Katona et al. [Reference Katona, Nemetz and Simonovits23], is called the Turán density of
$\pi (F) = \lim _{n\to \infty } \mathrm{ex}(n, \mathcal{F})/\binom{n}{2}$
, whose existence was proved by Katona et al. [Reference Katona, Nemetz and Simonovits23], is called the Turán density of
![]() $\mathcal{F}$
.
$\mathcal{F}$
.
For a graph
![]() $G$
we use
$G$
we use
![]() $V(G)$
to denote the vertex set of
$V(G)$
to denote the vertex set of
![]() $G$
, and use
$G$
, and use
![]() $v(G)$
and
$v(G)$
and
![]() $e(G)$
to denote the number of vertices and edges in
$e(G)$
to denote the number of vertices and edges in
![]() $G$
, respectively. For a set
$G$
, respectively. For a set
![]() $S \subset V(G)$
we use
$S \subset V(G)$
we use
![]() $e_{G}(S)$
to denote the number of edges in the induced subgraph
$e_{G}(S)$
to denote the number of edges in the induced subgraph
![]() $G[S]$
. Given two vertex sets
$G[S]$
. Given two vertex sets
![]() $X, Y \subset V(G)$
we use
$X, Y \subset V(G)$
we use
![]() $e_{G}(X,Y)$
to denote the number of edges in
$e_{G}(X,Y)$
to denote the number of edges in
![]() $G$
that have one vertex in
$G$
that have one vertex in
![]() $X$
and one vertex in
$X$
and one vertex in
![]() $Y$
(here edges with both vertices in
$Y$
(here edges with both vertices in
![]() $X\cap Y$
are counted twice, hence
$X\cap Y$
are counted twice, hence
![]() $e_{G}(X,X) = 2e_{G}(X)$
). We will omit the subscript
$e_{G}(X,X) = 2e_{G}(X)$
). We will omit the subscript
![]() $G$
if it is clear from the context.
$G$
if it is clear from the context.
Informally, we say that a graph is pseudorandom if its edge distribution behaves like a random graph. In this note we use the following notation, which was firstly introduced by Thomason in his fundamental papers [Reference Thomason38, Reference Thomason39], to quantify the randomness of a graph.
For two real numbers
![]() $p\in [0,1]$
and
$p\in [0,1]$
and
![]() $\alpha \ge 0$
, we say a graph
$\alpha \ge 0$
, we say a graph
![]() $G$
is
$G$
is
![]() $(p,\alpha )$
-jumbled if it satisfies
$(p,\alpha )$
-jumbled if it satisfies
for all
![]() $X,Y\subset V(G)$
.
$X,Y\subset V(G)$
.
A special family of
![]() $(p,\alpha )$
-jumbled graphs are the well known
$(p,\alpha )$
-jumbled graphs are the well known
![]() $(n,d,\lambda )$
-graphs. A graph
$(n,d,\lambda )$
-graphs. A graph
![]() $G$
is an
$G$
is an
![]() $(n,d,\lambda )$
-graph if it is a
$(n,d,\lambda )$
-graph if it is a
![]() $d$
-regular graph on
$d$
-regular graph on
![]() $n$
vertices and the second largest eigenvalue in absolute value of its adjacency matrix is
$n$
vertices and the second largest eigenvalue in absolute value of its adjacency matrix is
![]() $\lambda$
. The well known Expander Mixing Lemma (e.g. see [Reference Krivelevich and Sudakov27, Theorem 2.11]) implies that an
$\lambda$
. The well known Expander Mixing Lemma (e.g. see [Reference Krivelevich and Sudakov27, Theorem 2.11]) implies that an
![]() $(n,d,\lambda )$
-graph is
$(n,d,\lambda )$
-graph is
![]() $(d/n, \lambda )$
-jumbled. Conversely, Bilu and Linial [Reference Bilu and Linial9] proved that an
$(d/n, \lambda )$
-jumbled. Conversely, Bilu and Linial [Reference Bilu and Linial9] proved that an
![]() $n$
-vertex
$n$
-vertex
![]() $d$
-regular
$d$
-regular
![]() $(p,\alpha )$
-jumbled graph is an
$(p,\alpha )$
-jumbled graph is an
![]() $(n, d, \lambda )$
-graph with
$(n, d, \lambda )$
-graph with
![]() $\lambda = O(\alpha \log (d/\alpha ))$
.
$\lambda = O(\alpha \log (d/\alpha ))$
.
It is known that a random graph
![]() $G(n,p)$
is almost surely a
$G(n,p)$
is almost surely a
![]() $(p,\alpha )$
-jumbled graph with
$(p,\alpha )$
-jumbled graph with
![]() $\alpha = O(\sqrt{np})$
(see e.g. [Reference Krivelevich and Sudakov27, Corollary 2.3]). The proof of Erdős and Spencer in [Reference Erdős and Spencer21] can be extended to show that every
$\alpha = O(\sqrt{np})$
(see e.g. [Reference Krivelevich and Sudakov27, Corollary 2.3]). The proof of Erdős and Spencer in [Reference Erdős and Spencer21] can be extended to show that every
![]() $(p,\alpha )$
-jumbled graph on
$(p,\alpha )$
-jumbled graph on
![]() $n$
vertices satisfies that
$n$
vertices satisfies that
![]() $\alpha = \Omega (\sqrt{np})$
(see e.g. [Reference Bollobás and Scott12, Reference Krivelevich and Sudakov27]), and, in particular,
$\alpha = \Omega (\sqrt{np})$
(see e.g. [Reference Bollobás and Scott12, Reference Krivelevich and Sudakov27]), and, in particular,
![]() $\lambda = \Omega (\sqrt{d})$
for an
$\lambda = \Omega (\sqrt{d})$
for an
![]() $(n,d,\lambda )$
-graph. Therefore, an
$(n,d,\lambda )$
-graph. Therefore, an
![]() $n$
-vertex
$n$
-vertex
![]() $(p,\alpha )$
-jumbled graph with
$(p,\alpha )$
-jumbled graph with
![]() $\alpha = \Theta (\sqrt{np})$
can be viewed as optimally pseudorandom. The tightness of the bound
$\alpha = \Theta (\sqrt{np})$
can be viewed as optimally pseudorandom. The tightness of the bound
![]() $\lambda = \Omega (\sqrt{d})$
in general is also witnessed by many well known explicit constructions. For example, the well known triangle-free
$\lambda = \Omega (\sqrt{d})$
in general is also witnessed by many well known explicit constructions. For example, the well known triangle-free
![]() $(n,d,\lambda )$
-graph constructed by Alon [Reference Alon2] satisfies
$(n,d,\lambda )$
-graph constructed by Alon [Reference Alon2] satisfies
![]() $d = \Theta (n^{2/3})$
and
$d = \Theta (n^{2/3})$
and
![]() $\lambda = O(\sqrt{d})$
.
$\lambda = O(\sqrt{d})$
.
Constructions of dense pseudorandom graphs that avoid a certain graph as a subgraph are extremely useful for many problems. In particular, the second author and Verstraëte [Reference Mubayi and Verstraëte32] recently showed that for every fixed integer
![]() $t\ge 3$
, the existence of
$t\ge 3$
, the existence of
![]() $K_t$
-free
$K_t$
-free
![]() $(n,d,\lambda )$
-graphs with
$(n,d,\lambda )$
-graphs with
![]() $d = \Omega (n^{1-\frac{1}{2t-3}})$
and
$d = \Omega (n^{1-\frac{1}{2t-3}})$
and
![]() $\lambda = O(\sqrt{d})$
implies the lower bound
$\lambda = O(\sqrt{d})$
implies the lower bound
![]() $R(t,n) = \Omega ^{\ast }(n^{t-1})$
for the off-diagonal Ramsey numbers, and this matches the best known upper bound in exponent (see [Reference Mattheus and Verstraete31] for recent breakthrough result on
$R(t,n) = \Omega ^{\ast }(n^{t-1})$
for the off-diagonal Ramsey numbers, and this matches the best known upper bound in exponent (see [Reference Mattheus and Verstraete31] for recent breakthrough result on
![]() $R(4,n)$
). More generally, [Reference Mubayi and Verstraëte32] shows that the existence of dense
$R(4,n)$
). More generally, [Reference Mubayi and Verstraëte32] shows that the existence of dense
![]() $F$
-free pseudorandom graphs implies a good lower bound for the Ramsey number
$F$
-free pseudorandom graphs implies a good lower bound for the Ramsey number
![]() $R(F, n)$
. This motivates us to consider the following pseudorandom version of the Turán problem.
$R(F, n)$
. This motivates us to consider the following pseudorandom version of the Turán problem.
Let
![]() $\mathcal{F}$
be a family of graphs and
$\mathcal{F}$
be a family of graphs and
![]() $C\gt 0$
be a real number. Let
$C\gt 0$
be a real number. Let
![]() $\mathrm{ex}_{\mathrm{rand}}(n,C,\mathcal{F})$
be the maximum number of edges in an
$\mathrm{ex}_{\mathrm{rand}}(n,C,\mathcal{F})$
be the maximum number of edges in an
![]() $n$
-vertex
$n$
-vertex
![]() $(p,\alpha )$
-jumbled
$(p,\alpha )$
-jumbled
![]() $\mathcal{F}$
-free graph with
$\mathcal{F}$
-free graph with
![]() $\alpha \le C\sqrt{np}$
. Note that in the definition of
$\alpha \le C\sqrt{np}$
. Note that in the definition of
![]() $\mathrm{ex}_{\mathrm{rand}}(n,C,\mathcal{F})$
we do not have any restriction on
$\mathrm{ex}_{\mathrm{rand}}(n,C,\mathcal{F})$
we do not have any restriction on
![]() $p$
.
$p$
.
In many applications, it suffices to know the exponent of
![]() $\mathrm{ex}_{\mathrm{rand}}(n,C,\mathcal{F})$
. So we let
$\mathrm{ex}_{\mathrm{rand}}(n,C,\mathcal{F})$
. So we let
In other words,
![]() $\mathrm{exp}(\mathcal{F})$
is the supremum of
$\mathrm{exp}(\mathcal{F})$
is the supremum of
![]() $\beta$
such that there exist a constant
$\beta$
such that there exist a constant
![]() $C$
and a sequence
$C$
and a sequence
![]() $\left (G_n\right )_{n=1}^{\infty }$
of
$\left (G_n\right )_{n=1}^{\infty }$
of
![]() $\mathcal{F}$
-free
$\mathcal{F}$
-free
![]() $(p_n,\alpha _n)$
-jumbled graphs with
$(p_n,\alpha _n)$
-jumbled graphs with
Using the Expander Mixing Lemma one can prove that for every integer
![]() $t\ge 3$
we have
$t\ge 3$
we have
![]() $\mathrm{exp}(K_t) \le 1 - \frac{1}{2t-3}$
. Alon’s construction [Reference Alon2] shows that this bound is tight for
$\mathrm{exp}(K_t) \le 1 - \frac{1}{2t-3}$
. Alon’s construction [Reference Alon2] shows that this bound is tight for
![]() $t=3$
, that is,
$t=3$
, that is,
![]() $\mathrm{exp}(K_3) = \frac{2}{3}$
. It is a major open problem to determine
$\mathrm{exp}(K_3) = \frac{2}{3}$
. It is a major open problem to determine
![]() $\mathrm{exp}(K_t)$
in general. Alon and Krivelevich proved in [Reference Alon and Krivelevich4] that
$\mathrm{exp}(K_t)$
in general. Alon and Krivelevich proved in [Reference Alon and Krivelevich4] that
![]() $\mathrm{exp}(K_t) \ge 1- \frac{1}{t}$
. Recently, Bishnoi, Ihringer, and Pepe [Reference Bishnoi, Ihringer and Pepe10] improved their bound and proved the following result.
$\mathrm{exp}(K_t) \ge 1- \frac{1}{t}$
. Recently, Bishnoi, Ihringer, and Pepe [Reference Bishnoi, Ihringer and Pepe10] improved their bound and proved the following result.
Theorem 1.1 (Bishnoi et al. [Reference Bishnoi, Ihringer and Pepe10]). It holds that
![]() $\mathrm{exp}(K_t) \ge 1- \frac{1}{t-1}$
for all integers
$\mathrm{exp}(K_t) \ge 1- \frac{1}{t-1}$
for all integers
![]() $t \ge 4$
.
$t \ge 4$
.
Mattheus and Pavese [Reference Mattheus and Pavese30] give a different construction of
![]() $K_{t}$
-free pseudorandom graphs which also matches the bound in Theorem 1.1. In Section 4, we will present a construction that is isomorphic to the construction of Bishnoi et al. [Reference Bishnoi, Ihringer and Pepe10], and give a new proof to Theorem 1.1.
$K_{t}$
-free pseudorandom graphs which also matches the bound in Theorem 1.1. In Section 4, we will present a construction that is isomorphic to the construction of Bishnoi et al. [Reference Bishnoi, Ihringer and Pepe10], and give a new proof to Theorem 1.1.
For bipartite graphs, the pseudorandom version of the Turán problem does not appear to differ much from the ordinary Turán problem since many constructions for the lower bound are pseudorandom. For example, for complete bipartite graphs, the projective norm graphs (see [Reference Alon, Rónyai and Szabó5, Reference Kollár, Rónyai and Szabó25]) are optimally pseudorandom (see [Reference Szabó36]) and do not contain
![]() $K_{s,t}$
with
$K_{s,t}$
with
![]() $t\ge (s-1)!+1$
. Therefore, together with the well known Kövari–Sós–Turán Theorem [Reference Kövari, Sós and Turán26], we know that
$t\ge (s-1)!+1$
. Therefore, together with the well known Kövari–Sós–Turán Theorem [Reference Kövari, Sós and Turán26], we know that
![]() $\mathrm{exp}(K_{s,t}) = 1-\frac{1}{s}$
for all positive integers
$\mathrm{exp}(K_{s,t}) = 1-\frac{1}{s}$
for all positive integers
![]() $s,t$
with
$s,t$
with
![]() $t\ge (s-1)!+1$
. For even cycles, constructions from generalised polygons [Reference Lazebnik, Ustimenko and Woldar28] and an old result of Bondy and Simonovits [Reference Bondy and Simonovits13] imply that
$t\ge (s-1)!+1$
. For even cycles, constructions from generalised polygons [Reference Lazebnik, Ustimenko and Woldar28] and an old result of Bondy and Simonovits [Reference Bondy and Simonovits13] imply that
![]() $\mathrm{exp}(C_6) = \frac{1}{3}$
and
$\mathrm{exp}(C_6) = \frac{1}{3}$
and
![]() $\mathrm{exp}(C_{10}) = \frac{1}{5}$
. The value of
$\mathrm{exp}(C_{10}) = \frac{1}{5}$
. The value of
![]() $\mathrm{exp}(C_{2k})$
for
$\mathrm{exp}(C_{2k})$
for
![]() $k \neq 2,3,5$
are still unknown due to the lack of constructions. For non-bipartite graphs,
$k \neq 2,3,5$
are still unknown due to the lack of constructions. For non-bipartite graphs,
![]() $\mathrm{exp}(F)$
is completely different from the ordinary Turán problem (indeed,
$\mathrm{exp}(F)$
is completely different from the ordinary Turán problem (indeed,
![]() $\mathrm{exp}(F)\lt 2$
while
$\mathrm{exp}(F)\lt 2$
while
![]() $\pi (F) \gt 0$
) and there are very graphs
$\pi (F) \gt 0$
) and there are very graphs
![]() $F$
for which
$F$
for which
![]() $\mathrm{exp}(F)$
is known. For example, for odd cycles, a construction due to Alon and Kahale [Reference Alon and Kahale3] together with Proposition 4.12 in [Reference Krivelevich and Sudakov27] implies that
$\mathrm{exp}(F)$
is known. For example, for odd cycles, a construction due to Alon and Kahale [Reference Alon and Kahale3] together with Proposition 4.12 in [Reference Krivelevich and Sudakov27] implies that
![]() $\mathrm{exp}(C_{\ell }) = \frac{2}{\ell }$
for all odd integers
$\mathrm{exp}(C_{\ell }) = \frac{2}{\ell }$
for all odd integers
![]() $\ell \ge 3$
.
$\ell \ge 3$
.
The first general upper bound on
![]() $\exp (F)$
, is due to Kohayakawa et al. [Reference Kohayakawa, Rödl, Schacht, Sissokho and Skokan24]. They prove that
$\exp (F)$
, is due to Kohayakawa et al. [Reference Kohayakawa, Rödl, Schacht, Sissokho and Skokan24]. They prove that
![]() $\mathrm{exp}(F) \le 1 - \frac{1}{2\nu (F)-1}$
for every triangle-free graph
$\mathrm{exp}(F) \le 1 - \frac{1}{2\nu (F)-1}$
for every triangle-free graph
![]() $F$
. Here
$F$
. Here
![]() $\nu (F) = \frac{1}{2}\left (d(F) + D(F) +1\right )$
, where
$\nu (F) = \frac{1}{2}\left (d(F) + D(F) +1\right )$
, where
![]() $D(F) = \min \left \{2d(F), \Delta (F)\right \}$
and
$D(F) = \min \left \{2d(F), \Delta (F)\right \}$
and
![]() $d(F)$
is the degeneracy of
$d(F)$
is the degeneracy of
![]() $F$
. This was improved via the following result of Conlon et al. in [Reference Conlon, Fox and Zhao17].
$F$
. This was improved via the following result of Conlon et al. in [Reference Conlon, Fox and Zhao17].
Theorem 1.2 (Conlon et al. [Reference Conlon, Fox and Zhao17]). For every graph
![]() $F$
, we have
$F$
, we have
![]() $\mathrm{exp}(F) \le 1-\frac{1}{2d_2(F)+1}$
, where
$\mathrm{exp}(F) \le 1-\frac{1}{2d_2(F)+1}$
, where
![]() $d_2(F)$
is the minimum real number
$d_2(F)$
is the minimum real number
![]() $d$
such that there is an ordering of the vertices
$d$
such that there is an ordering of the vertices
![]() $v_1, \ldots, v_m$
of
$v_1, \ldots, v_m$
of
![]() $F$
so that
$F$
so that
![]() $N_{\lt i}(v_i)+N_{\lt i}(v_j) \le 2d$
for all edges
$N_{\lt i}(v_i)+N_{\lt i}(v_j) \le 2d$
for all edges
![]() $v_i v_j \in F$
. Here
$v_i v_j \in F$
. Here
![]() $N_{\lt i}(v)$
is the number of neighbours of
$N_{\lt i}(v)$
is the number of neighbours of
![]() $v$
in
$v$
in
![]() $\{v_1, \ldots, v_{i-1}\}$
.
$\{v_1, \ldots, v_{i-1}\}$
.
In some cases, the bound provided by Theorem 1.2 is sharp (e.g. it is conjectured to be sharp for cliques), but we speculate that for most graphs
![]() $F$
it can be improved. Below we give an improvement that holds for many graphs.
$F$
it can be improved. Below we give an improvement that holds for many graphs.
Theorem 1.3.
Let
![]() $F$
be a fixed graph and
$F$
be a fixed graph and
![]() $d$
be such that the following holds. There exists an ordering
$d$
be such that the following holds. There exists an ordering
![]() $v_1,v_2, \ldots, v_m$
of the vertices of
$v_1,v_2, \ldots, v_m$
of the vertices of
![]() $F$
and a
$F$
and a
![]() $1 \leq k \leq m$
such that:
$1 \leq k \leq m$
such that:
-
•
 $F[\{v_{k}, \ldots, v_m\}]$
is a forest,
$F[\{v_{k}, \ldots, v_m\}]$
is a forest,
-
• for all edges
 $v_iv_j \in F$
with
$v_iv_j \in F$
with
 $i\lt j$
,
$i\lt j$
,
 $i\lt k$
, we have
$i\lt k$
, we have
 $N_{\lt i}(v_i) + N_{\lt i}(v_j) \leq 2d$
, and
$N_{\lt i}(v_i) + N_{\lt i}(v_j) \leq 2d$
, and
-
• for all edges
 $v_iv_j \in F$
with
$v_iv_j \in F$
with
 $k \leq i \lt j$
, we have
$k \leq i \lt j$
, we have
 $N_{\lt k}(v_i) + N_{\lt k}(v_j) \leq 2d$
.
$N_{\lt k}(v_i) + N_{\lt k}(v_j) \leq 2d$
.
Then,
![]() $\mathrm{exp}(F) \leq 1 - \frac{1}{2d+1}$
.
$\mathrm{exp}(F) \leq 1 - \frac{1}{2d+1}$
.
Remark 1. Roughly speaking, Theorem 1.3 says that if there exists an induced forest on an interval of some ordering of
![]() $V(F)$
, then it is possible to improve the bound of Theorem 1.2 by treating this forest as one edge. In fact, we will see later that the proof of Theorem 1.3 can be extended easily to get a more general result (see Theorem 2.5). In addition, it was observed by a referee that only one-sided jumbledness, namely
$V(F)$
, then it is possible to improve the bound of Theorem 1.2 by treating this forest as one edge. In fact, we will see later that the proof of Theorem 1.3 can be extended easily to get a more general result (see Theorem 2.5). In addition, it was observed by a referee that only one-sided jumbledness, namely
![]() $e(X,Y) - p|X||Y| \ge -\alpha \sqrt{|X||Y|}$
, is necessary to prove all of the results,
$e(X,Y) - p|X||Y| \ge -\alpha \sqrt{|X||Y|}$
, is necessary to prove all of the results,
As an application of Theorem 1.3, we present an upper bound for
![]() $\mathrm{exp}(\textbf{P})$
, where
$\mathrm{exp}(\textbf{P})$
, where
![]() $\textbf{P}$
is the Petersen graph. The Petersen graph was considered by several researchers in related contexts. For example, Tait and Timmons [Reference Tait and Timmons37] proved that the Erdős–Rényi orthogonal polarity graphs [Reference Erdős and Rényi20] (henceforth the Erdős–Rényi graph), which are optimally pseudorandom
$\textbf{P}$
is the Petersen graph. The Petersen graph was considered by several researchers in related contexts. For example, Tait and Timmons [Reference Tait and Timmons37] proved that the Erdős–Rényi orthogonal polarity graphs [Reference Erdős and Rényi20] (henceforth the Erdős–Rényi graph), which are optimally pseudorandom
![]() $C_4$
-free graphs, contain the Petersen graph as a subgraph. Conlon et al. asked in [Reference Conlon, Fox, Sudakov and Zhao16] whether there is a counting lemma for the Petersen graph in an
$C_4$
-free graphs, contain the Petersen graph as a subgraph. Conlon et al. asked in [Reference Conlon, Fox, Sudakov and Zhao16] whether there is a counting lemma for the Petersen graph in an
![]() $n$
-vertex
$n$
-vertex
![]() $C_4$
-free graph with
$C_4$
-free graph with
![]() $\Omega (n^{3/2})$
edges. We know very little about
$\Omega (n^{3/2})$
edges. We know very little about
![]() $\mathrm{exp}(\textbf{P})$
, for example, it is not known whether
$\mathrm{exp}(\textbf{P})$
, for example, it is not known whether
![]() $\mathrm{exp}(\textbf{P}) \ge \frac{1}{2}$
. The only lower bound we have is
$\mathrm{exp}(\textbf{P}) \ge \frac{1}{2}$
. The only lower bound we have is
![]() $\mathrm{exp}(\textbf{P}) \ge \mathrm{exp}(C_5) = \frac{2}{5}$
. In the other direction, the previous best upper bound is
$\mathrm{exp}(\textbf{P}) \ge \mathrm{exp}(C_5) = \frac{2}{5}$
. In the other direction, the previous best upper bound is
![]() $\mathrm{exp}(\textbf{P}) \le \frac{3}{4}$
that follows from [Reference Conlon, Fox and Zhao17] (it is not too difficult to prove that
$\mathrm{exp}(\textbf{P}) \le \frac{3}{4}$
that follows from [Reference Conlon, Fox and Zhao17] (it is not too difficult to prove that
![]() $d_2(\textbf{P}) = \frac{3}{2}$
).
$d_2(\textbf{P}) = \frac{3}{2}$
).

Figure 1. The induced subgraph of
![]() $\textbf{P}$
on
$\textbf{P}$
on
![]() $\{2,4,5,7,8,10\}$
is a tree.
$\{2,4,5,7,8,10\}$
is a tree.
Theorem 1.4.
We have
![]() $\mathrm{exp}(\textbf{P}) \le \frac{2}{3}$
.
$\mathrm{exp}(\textbf{P}) \le \frac{2}{3}$
.
It is easy to observe that Theorem 1.4 follows from Theorem 1.3 by letting the ordering of
![]() $V(\textbf{P})$
be
$V(\textbf{P})$
be
![]() $(v_1, \ldots, v_{10}) = (1,3,6,9,2,4,5,7,8,10)$
and choosing
$(v_1, \ldots, v_{10}) = (1,3,6,9,2,4,5,7,8,10)$
and choosing
![]() $k=5$
(see Figure 1). We conjecture that
$k=5$
(see Figure 1). We conjecture that
![]() $\mathrm{exp}(\textbf{P}) = \frac{2}{3}$
. We think that the construction of
$\mathrm{exp}(\textbf{P}) = \frac{2}{3}$
. We think that the construction of
![]() $K_3$
-free pseudorandom graphs due to Kopparty does not contain the Petersen graph as a subgraph. If this is true, then it will prove the lower bound
$K_3$
-free pseudorandom graphs due to Kopparty does not contain the Petersen graph as a subgraph. If this is true, then it will prove the lower bound
![]() $\mathrm{exp}(\textbf{P}) \ge \frac{2}{3}$
. For completeness, we include his construction here.
$\mathrm{exp}(\textbf{P}) \ge \frac{2}{3}$
. For completeness, we include his construction here.
Let
![]() $p\neq 3$
be a prime, and let
$p\neq 3$
be a prime, and let
![]() $\mathbb{F}_{q}$
be a finite field with where
$\mathbb{F}_{q}$
be a finite field with where
![]() $q = p^h$
for some integer
$q = p^h$
for some integer
![]() $h\ge 1$
. Recall that the absolute trace function
$h\ge 1$
. Recall that the absolute trace function
![]() $\mathrm{Tr}\colon \mathbb{F}_{q} \to \mathbb{F}_{p}$
is defined as
$\mathrm{Tr}\colon \mathbb{F}_{q} \to \mathbb{F}_{p}$
is defined as
![]() $\mathrm{Tr}(\alpha ) = \alpha + \alpha ^{p} + \cdots + \alpha ^{p^{h-1}}$
for every
$\mathrm{Tr}(\alpha ) = \alpha + \alpha ^{p} + \cdots + \alpha ^{p^{h-1}}$
for every
![]() $\alpha \in \mathbb{F}_{q}$
.
$\alpha \in \mathbb{F}_{q}$
.
Let
![]() $V = \mathbb{F}_{q}^{3}$
,
$V = \mathbb{F}_{q}^{3}$
,
![]() $T = \left \{x \in \mathbb{F}_{q} \colon \mathrm{Tr}(x) \in \{1, -1\}\right \}$
, and
$T = \left \{x \in \mathbb{F}_{q} \colon \mathrm{Tr}(x) \in \{1, -1\}\right \}$
, and
![]() $S\subset \mathbb{F}_{q}^3$
be a subset defined as
$S\subset \mathbb{F}_{q}^3$
be a subset defined as
Kopparty’s construction is the graph
![]() $G$
on
$G$
on
![]() $V$
in which two vertices
$V$
in which two vertices
![]() $\textbf{u}, \textbf{v} \in V$
are adjacent iff
$\textbf{u}, \textbf{v} \in V$
are adjacent iff
![]() $\textbf{u}-\textbf{v} \in S$
. Using some simple linear algebra one can show that
$\textbf{u}-\textbf{v} \in S$
. Using some simple linear algebra one can show that
![]() $G$
is triangle-free, and using some results about finite fields and abelian groups one can prove that
$G$
is triangle-free, and using some results about finite fields and abelian groups one can prove that
![]() $G$
is an
$G$
is an
![]() $(n,d,\lambda )$
-graph with
$(n,d,\lambda )$
-graph with
![]() $n = q^3$
,
$n = q^3$
,
![]() $d = \Theta (\frac{q^2}{p})$
, and
$d = \Theta (\frac{q^2}{p})$
, and
![]() $\lambda = \Theta (\frac{q}{p})$
.
$\lambda = \Theta (\frac{q}{p})$
.
Remark 2. Ferdinand Ihringer informed us that the construction above contains an induced copy of the Petersen graph when
![]() $p=2$
and
$p=2$
and
![]() $h=3$
, and he thinks that, in general, Kopparty’s construction contains many copies of the Petersen graph. Nevertheless, it is still might be true that
$h=3$
, and he thinks that, in general, Kopparty’s construction contains many copies of the Petersen graph. Nevertheless, it is still might be true that
![]() $\mathrm{exp}(\textbf{P}) = \frac{2}{3}$
.
$\mathrm{exp}(\textbf{P}) = \frac{2}{3}$
.
Our next result about
![]() $K_{2,3}$
was motivated by an old problem of Erdős [Reference Erdős19], which asks if
$K_{2,3}$
was motivated by an old problem of Erdős [Reference Erdős19], which asks if
is true. A construction due to Parsons [Reference Parsons33] for the lower bound comes from the Erdős–Rényi graph by removing half of its vertices. Since the Erdős–Rényi graph is optimally pseudorandom, Parsons’ construction also implies that
![]() $\mathrm{ex}_{\mathrm{rand}}(n,C,\{K_3, C_4\}) \ge \left (\frac{1}{2\sqrt{2}}+o(1)\right )n^{3/2}$
for some absolute constant
$\mathrm{ex}_{\mathrm{rand}}(n,C,\{K_3, C_4\}) \ge \left (\frac{1}{2\sqrt{2}}+o(1)\right )n^{3/2}$
for some absolute constant
![]() $C$
. In [Reference Allen, Keevash, Sudakov and Verstraëte1], Allen, Keevash, Sudakov, and Verstraëte proved that the extremal constructions for
$C$
. In [Reference Allen, Keevash, Sudakov and Verstraëte1], Allen, Keevash, Sudakov, and Verstraëte proved that the extremal constructions for
![]() $\mathrm{ex}(n,\{K_3, K_{2,t}\})$
cannot be bipartite for every
$\mathrm{ex}(n,\{K_3, K_{2,t}\})$
cannot be bipartite for every
![]() $t\ge 3$
by constructing a
$t\ge 3$
by constructing a
![]() $\{K_3, K_{2,t}\}$
-free graph whose number of edges is greater than the maximum number of edges in a
$\{K_3, K_{2,t}\}$
-free graph whose number of edges is greater than the maximum number of edges in a
![]() $\{K_3, K_{2,t}\}$
-free bipartite graph. However, their construction is
$\{K_3, K_{2,t}\}$
-free bipartite graph. However, their construction is
![]() $(t-1)$
-partite, and therefore it does not give a lower bound for
$(t-1)$
-partite, and therefore it does not give a lower bound for
![]() $\mathrm{ex}_{\mathrm{rand}}(n,C,\{K_3, K_{2,3}\})$
. The previous best lower bound is
$\mathrm{ex}_{\mathrm{rand}}(n,C,\{K_3, K_{2,3}\})$
. The previous best lower bound is
that follows from Parsons’ construction. We improve this and present a construction of the densest known
![]() $\{K_3, K_{2,3}\}$
-free pseudorandom graphs.
$\{K_3, K_{2,3}\}$
-free pseudorandom graphs.
Theorem 1.5.
We have
![]() $\mathrm{ex}_{\mathrm{rand}}(n,2,\{K_3, K_{2,3}\}) \ge \left (\frac{1}{2}-o(1)\right )n^{3/2}$
.
$\mathrm{ex}_{\mathrm{rand}}(n,2,\{K_3, K_{2,3}\}) \ge \left (\frac{1}{2}-o(1)\right )n^{3/2}$
.
Remark 3. Thang Pham pointed out to us that the following constructionFootnote 1 also provides a lower bound for
![]() $\mathrm{ex}_{\mathrm{rand}}(n,2,\{K_3, K_{2,3}\})$
. Let
$\mathrm{ex}_{\mathrm{rand}}(n,2,\{K_3, K_{2,3}\})$
. Let
![]() $q$
be an odd prime power. The distance graph
$q$
be an odd prime power. The distance graph
![]() $D$
on
$D$
on
![]() $\mathbb{F}_{q}^2$
is a graph whose vertex set is
$\mathbb{F}_{q}^2$
is a graph whose vertex set is
![]() $\mathbb{F}_{q}^2$
, and two points
$\mathbb{F}_{q}^2$
, and two points
![]() $(x_1,x_2), (y_1, y_2)$
are adjacent iff
$(x_1,x_2), (y_1, y_2)$
are adjacent iff
![]() $(x_1-y_1)^2+(x_2-y_2)^2=1$
. The
$(x_1-y_1)^2+(x_2-y_2)^2=1$
. The
![]() $K_{2,3}$
-freeness of
$K_{2,3}$
-freeness of
![]() $D$
follows from the fact that any two cycles have at most two points in the intersection. The
$D$
follows from the fact that any two cycles have at most two points in the intersection. The
![]() $K_3$
-freeness of
$K_3$
-freeness of
![]() $D$
follows from results in [Reference Bennett, Iosevich and Pakianathan8]. The pseudorandomness of
$D$
follows from results in [Reference Bennett, Iosevich and Pakianathan8]. The pseudorandomness of
![]() $D$
follows from results in [Reference Iosevich and Rudnev22]. Additionally, a referee informed us that constructions in an even earlier work by Bannai et al. [Reference Bannai, Shimabukuro and Tanaka7] also satisfy the desired properties.
$D$
follows from results in [Reference Iosevich and Rudnev22]. Additionally, a referee informed us that constructions in an even earlier work by Bannai et al. [Reference Bannai, Shimabukuro and Tanaka7] also satisfy the desired properties.
In Section 2, we prove Theorems 1.3. In Section 3, we prove Theorem 1.5. In Section 4 we present a new proof of Theorem 1.1. Throughout the paper, we will omit the use of floors and ceilings to make the presentation cleaner.
2. Proof of Theorem 1.3
We prove Theorem 1.3 in this section.
Let us present two standard lemmas. We start with the following direct consequence of the definition of a jumbled graph.
Lemma 2.1.
Fix a real number
![]() $q \gt 1$
. Let
$q \gt 1$
. Let
![]() $G$
be a
$G$
be a
![]() $(p,\alpha )$
-jumbled graph on
$(p,\alpha )$
-jumbled graph on
![]() $n$
vertices and let
$n$
vertices and let
![]() $X,Y_1, \ldots, Y_{m} \subseteq V(G)$
be pairwise disjoint subsets. If
$X,Y_1, \ldots, Y_{m} \subseteq V(G)$
be pairwise disjoint subsets. If
![]() $|X||Y_i| \geq q^2m\left (\frac{\alpha }{p} \right )^2$
for all
$|X||Y_i| \geq q^2m\left (\frac{\alpha }{p} \right )^2$
for all
![]() $i\in [m]$
, then there exists a vertex
$i\in [m]$
, then there exists a vertex
![]() $x \in X$
with at least
$x \in X$
with at least
![]() $\frac{q-1}{q}p|Y_i|$
neighbours in
$\frac{q-1}{q}p|Y_i|$
neighbours in
![]() $Y_i$
for all
$Y_i$
for all
![]() $i\in [m]$
. In particular,
$i\in [m]$
. In particular,
![]() $e(X,Y_i) \gt 0$
for all
$e(X,Y_i) \gt 0$
for all
![]() $i\in [m]$
.
$i\in [m]$
.
Proof. Define
![]() $X_i \;:\!=\; \{v\in X \colon |N_{G}(v) \cap Y_i| \lt \frac{q-1}{q}p|Y_i|\}$
for
$X_i \;:\!=\; \{v\in X \colon |N_{G}(v) \cap Y_i| \lt \frac{q-1}{q}p|Y_i|\}$
for
![]() $i\in [m]$
. It suffices to prove that
$i\in [m]$
. It suffices to prove that
![]() $|X_i| \lt \frac{|X|}{m}$
for all
$|X_i| \lt \frac{|X|}{m}$
for all
![]() $i\in [m]$
. Suppose to the contrary that
$i\in [m]$
. Suppose to the contrary that
![]() $|X_i| \ge \frac{|X|}{m}$
for some
$|X_i| \ge \frac{|X|}{m}$
for some
![]() $i\in [m]$
. By the definition of jumbleness, we get
$i\in [m]$
. By the definition of jumbleness, we get
It follows from
![]() $|X||Y_i| \geq q^2m\left (\frac{\alpha }{p} \right )^2$
that
$|X||Y_i| \geq q^2m\left (\frac{\alpha }{p} \right )^2$
that
![]() $\alpha \le \frac{p}{q} \sqrt{\frac{|X||Y_i|}{m}} \le \frac{p}{q} \sqrt{|X_i||Y_i|}$
. Therefore, it follows from the inequality above that
$\alpha \le \frac{p}{q} \sqrt{\frac{|X||Y_i|}{m}} \le \frac{p}{q} \sqrt{|X_i||Y_i|}$
. Therefore, it follows from the inequality above that
but our definition of
![]() $X_i$
yields
$X_i$
yields
![]() $e(X_i,Y_i) \lt \frac{q-1}{q} p |X_i||Y_i|$
, a contradiction.
$e(X_i,Y_i) \lt \frac{q-1}{q} p |X_i||Y_i|$
, a contradiction.
The next lemma is a simple cleaning procedure which is useful in problems concerning
![]() $(p,\alpha )$
-jumbled graphs.
$(p,\alpha )$
-jumbled graphs.
Lemma 2.2.
Let
![]() $G$
be a
$G$
be a
![]() $(p,\alpha )$
-jumbled graph on
$(p,\alpha )$
-jumbled graph on
![]() $n$
vertices. Then, for all sets
$n$
vertices. Then, for all sets
![]() $X,Y \subseteq V(G)$
such that
$X,Y \subseteq V(G)$
such that
![]() $|X||Y| \geq 100 (\alpha/ p)^2$
the following holds. There exist subsets
$|X||Y| \geq 100 (\alpha/ p)^2$
the following holds. There exist subsets
![]() $X' \subseteq X, Y' \subseteq Y$
respectively of size at least
$X' \subseteq X, Y' \subseteq Y$
respectively of size at least
![]() $9|X|/10$
and
$9|X|/10$
and
![]() $9|Y|/10$
such that all
$9|Y|/10$
such that all
![]() $v \in X'$
have
$v \in X'$
have
![]() $d(v,Y') \geq p|Y'|/10$
and all
$d(v,Y') \geq p|Y'|/10$
and all
![]() $u \in Y'$
have
$u \in Y'$
have
![]() $d(u,X') \geq p|X'|/10$
.
$d(u,X') \geq p|X'|/10$
.
Proof. Consider the following process. Start with
![]() $X_0 \;:\!=\; X, Y_0 \;:\!=\; Y$
and at step
$X_0 \;:\!=\; X, Y_0 \;:\!=\; Y$
and at step
![]() $i \geq 0$
, do the following. Take
$i \geq 0$
, do the following. Take
![]() $G_i \;:\!=\; G[X_i,Y_i]$
and if there exists a vertex
$G_i \;:\!=\; G[X_i,Y_i]$
and if there exists a vertex
![]() $v \in X_i$
such that
$v \in X_i$
such that
![]() $d(v,Y_i) \lt p|Y_i|/10$
or a vertex
$d(v,Y_i) \lt p|Y_i|/10$
or a vertex
![]() $v \in Y_i$
such that
$v \in Y_i$
such that
![]() $d(v,X_i) \lt p|X_i|/10$
, remove it from
$d(v,X_i) \lt p|X_i|/10$
, remove it from
![]() $X_i$
,
$X_i$
,
![]() $Y_i$
respectively, giving new
$Y_i$
respectively, giving new
![]() $X_{i+1},Y_{i+1}$
. We claim that this process stops before
$X_{i+1},Y_{i+1}$
. We claim that this process stops before
![]() $|X_i| \leq 9|X|/10$
or
$|X_i| \leq 9|X|/10$
or
![]() $|Y_i| \leq 9|Y|/10$
, which would imply that we are done. Indeed, if it did not stop before that, consider the step at which, w.l.o.g.,
$|Y_i| \leq 9|Y|/10$
, which would imply that we are done. Indeed, if it did not stop before that, consider the step at which, w.l.o.g.,
![]() $|X_i| = 9|X|/10$
and
$|X_i| = 9|X|/10$
and
![]() $|Y_i| \ge 9|Y|/10$
. By construction, every vertex in
$|Y_i| \ge 9|Y|/10$
. By construction, every vertex in
![]() $X \setminus X_i$
has less than
$X \setminus X_i$
has less than
![]() $p|Y|/10 \leq p|Y_i|/9$
neighbours in
$p|Y|/10 \leq p|Y_i|/9$
neighbours in
![]() $Y_i$
. So,
$Y_i$
. So,
On the other hand, the definition of a
![]() $(p,\alpha )$
-jumbled graph implies that
$(p,\alpha )$
-jumbled graph implies that
which is a contradiction since
![]() $|X \setminus X_i||Y_i| \geq \frac{1}{10} \cdot \frac{9}{10} \cdot |X||Y| \geq 4 \left (\frac{\alpha }{p} \right )^2$
.
$|X \setminus X_i||Y_i| \geq \frac{1}{10} \cdot \frac{9}{10} \cdot |X||Y| \geq 4 \left (\frac{\alpha }{p} \right )^2$
.
We also need the following embedding lemma for forests.
Lemma 2.3.
Suppose that
![]() $T$
is a forest on
$T$
is a forest on
![]() $[m]$
and
$[m]$
and
![]() $G$
is an
$G$
is an
![]() $n$
-vertex
$n$
-vertex
![]() $(p,\alpha )$
-jumbled graph. Let
$(p,\alpha )$
-jumbled graph. Let
![]() $X_1, \ldots, X_{m} \subset V(G)$
be nonempty pairwise disjoint subsets of
$X_1, \ldots, X_{m} \subset V(G)$
be nonempty pairwise disjoint subsets of
![]() $V(G)$
that satisfy
$V(G)$
that satisfy
for all edges
![]() $ij$
in
$ij$
in
![]() $T$
. Then there exists an embedding of
$T$
. Then there exists an embedding of
![]() $f\colon T \to G$
such that
$f\colon T \to G$
such that
![]() $f(i) \in X_i$
for all
$f(i) \in X_i$
for all
![]() $i\in [m]$
.
$i\in [m]$
.
Proof. We prove this lemma by induction on
![]() $m$
. The base case
$m$
. The base case
![]() $m=1$
is clear since
$m=1$
is clear since
![]() $X_1$
is nonempty. So we may assume that
$X_1$
is nonempty. So we may assume that
![]() $m \ge 2$
. Without loss of generality, we may assume that the vertex
$m \ge 2$
. Without loss of generality, we may assume that the vertex
![]() $m$
is a leaf of
$m$
is a leaf of
![]() $T$
and the vertex
$T$
and the vertex
![]() $m-1$
is its neighbour in
$m-1$
is its neighbour in
![]() $T$
. Let
$T$
. Let
![]() $T' \;:\!=\; T-m$
. Let
$T' \;:\!=\; T-m$
. Let
We claim that
![]() $|X'_{m-1}| \ge |X_{m-1}|/2$
. Indeed, suppose to the contrary that
$|X'_{m-1}| \ge |X_{m-1}|/2$
. Indeed, suppose to the contrary that
![]() $|X'_{m-1}| \lt |X_{m-1}|/2$
. Then we would have
$|X'_{m-1}| \lt |X_{m-1}|/2$
. Then we would have
![]() $|X_{m}||X_{m-1}\setminus X'_{m-1}| \ge |X_{m}||X_{m-1}|/2 \ge 2^{m-1}(\alpha/p)^2 \ge 2(\alpha/p)^2$
, it follows from Lemma 2.1 (with
$|X_{m}||X_{m-1}\setminus X'_{m-1}| \ge |X_{m}||X_{m-1}|/2 \ge 2^{m-1}(\alpha/p)^2 \ge 2(\alpha/p)^2$
, it follows from Lemma 2.1 (with
![]() $q=\sqrt{2}\gt 1$
) that
$q=\sqrt{2}\gt 1$
) that
![]() $e(X_m, X_{m-1}\setminus X'_{m-1})\gt 0$
. This contradicts the fact that
$e(X_m, X_{m-1}\setminus X'_{m-1})\gt 0$
. This contradicts the fact that
![]() $e(X_m, X_{m-1}\setminus X'_{m-1}) =0$
. Hence,
$e(X_m, X_{m-1}\setminus X'_{m-1}) =0$
. Hence,
![]() $|X'_{m-1}| \ge |X_{m-1}|/2$
.
$|X'_{m-1}| \ge |X_{m-1}|/2$
.
Now apply the induction hypothesis to the sets
![]() $X_1, \ldots, X_{m-2}, X'_{m-1}$
, we obtain an embedding
$X_1, \ldots, X_{m-2}, X'_{m-1}$
, we obtain an embedding
![]() $f \colon T' \to G$
such that
$f \colon T' \to G$
such that
![]() $f(i) \in X_i$
for
$f(i) \in X_i$
for
![]() $i\in [m-2]$
and
$i\in [m-2]$
and
![]() $f(m-1) \in X'_{m-1}$
. By the definition of
$f(m-1) \in X'_{m-1}$
. By the definition of
![]() $X'_{m-1}$
, there exists
$X'_{m-1}$
, there exists
![]() $v \in X_{m}$
such that
$v \in X_{m}$
such that
![]() $\{f(m-1), v\} \in G$
. Hence we can extend
$\{f(m-1), v\} \in G$
. Hence we can extend
![]() $f$
to get an embedding of
$f$
to get an embedding of
![]() $T$
to
$T$
to
![]() $G$
by setting
$G$
by setting
![]() $f(m) = v$
. This completes the proof of Lemma 2.3.
$f(m) = v$
. This completes the proof of Lemma 2.3.
Now we are ready to prove Theorem 1.3.
Proof of Theorem
1.3
. Let
![]() $G$
be a
$G$
be a
![]() $(p, \alpha )$
-jumbled graph with
$(p, \alpha )$
-jumbled graph with
![]() $\alpha \lt \frac{p^{d+1}n}{C}$
for an arbitrarily large constant
$\alpha \lt \frac{p^{d+1}n}{C}$
for an arbitrarily large constant
![]() $C \gt m4^m$
. We will show that
$C \gt m4^m$
. We will show that
![]() $G$
contains a copy of
$G$
contains a copy of
![]() $F$
. This implies that
$F$
. This implies that
![]() $\mathrm{exp}(F) \leq 1 - \frac{1}{2d+1}$
. Indeed, if
$\mathrm{exp}(F) \leq 1 - \frac{1}{2d+1}$
. Indeed, if
![]() $C_1\gt 0$
and
$C_1\gt 0$
and
![]() $C_2 \gt (C_1C)^{\frac{2}{2d+1}}$
and
$C_2 \gt (C_1C)^{\frac{2}{2d+1}}$
and
![]() $G$
is
$G$
is
![]() $(p, \alpha )$
-jumbled with
$(p, \alpha )$
-jumbled with
![]() $p \gt C_2 n^{-\frac{1}{2d+1}}$
and
$p \gt C_2 n^{-\frac{1}{2d+1}}$
and
![]() $\alpha \lt C_1\sqrt{pn}$
, then a short calculation shows that
$\alpha \lt C_1\sqrt{pn}$
, then a short calculation shows that
![]() $\alpha \lt \frac{p^{d+1}n}{C}$
and our result will imply the theorem.
$\alpha \lt \frac{p^{d+1}n}{C}$
and our result will imply the theorem.
Consider an ordering
![]() $v_1,v_2, \ldots, v_m$
of the vertices of
$v_1,v_2, \ldots, v_m$
of the vertices of
![]() $F$
and a
$F$
and a
![]() $1 \leq k \leq m$
such that:
$1 \leq k \leq m$
such that:
-
(i)
 $F[\{v_{k}, \ldots, v_m\}]$
is a forest,
$F[\{v_{k}, \ldots, v_m\}]$
is a forest, -
(ii) for all edges
 $v_iv_j \in F$
with
$v_iv_j \in F$
with
 $i\lt j$
,
$i\lt j$
,
 $i\lt k$
, we have
$i\lt k$
, we have
 $N_{\lt i}(v_i) + N_{\lt i}(v_j) \leq 2d$
, and
$N_{\lt i}(v_i) + N_{\lt i}(v_j) \leq 2d$
, and -
(iii) for all edges
 $v_iv_j \in F$
with
$v_iv_j \in F$
with
 $k \leq i \lt j$
, we have
$k \leq i \lt j$
, we have
 $N_{\lt k}(v_i) + N_{\lt k}(v_j) \leq 2d$
.
$N_{\lt k}(v_i) + N_{\lt k}(v_j) \leq 2d$
.
Let us denote
![]() $F[\{v_1, \ldots, v_{k-1}\}]$
by
$F[\{v_1, \ldots, v_{k-1}\}]$
by
![]() $F_1$
and
$F_1$
and
![]() $F[\{v_k, \ldots, v_m\}]$
by
$F[\{v_k, \ldots, v_m\}]$
by
![]() $F_2$
. We will first embed a copy of
$F_2$
. We will first embed a copy of
![]() $F_1$
using (b). At the same time, we will also ensure by (c), that the candidate sets for the vertices
$F_1$
using (b). At the same time, we will also ensure by (c), that the candidate sets for the vertices
![]() $v_k, \ldots, v_m$
are still large enough so that the forest
$v_k, \ldots, v_m$
are still large enough so that the forest
![]() $F_2$
can be embedded in them, thus giving an embedding of
$F_2$
can be embedded in them, thus giving an embedding of
![]() $F$
.
$F$
.
Take a partition
![]() $V(G) = V_1 \cup \cdots \cup V_{m}$
such that
$V(G) = V_1 \cup \cdots \cup V_{m}$
such that
![]() $|V_i| \ge \frac{n}{2m}$
for all
$|V_i| \ge \frac{n}{2m}$
for all
![]() $i\in [m]$
.
$i\in [m]$
.
Claim 2.4.
Let
![]() $s\in [k-1]$
. Then there exist vertices
$s\in [k-1]$
. Then there exist vertices
![]() $u_j \in V_j$
for all
$u_j \in V_j$
for all
![]() $j \in [s]$
such that
$j \in [s]$
such that
![]() $G[\{u_1, \ldots, u_{s}\}]$
contains a copy of
$G[\{u_1, \ldots, u_{s}\}]$
contains a copy of
![]() $F[\{v_1, \ldots, v_{s}\}]$
and
$F[\{v_1, \ldots, v_{s}\}]$
and
 \begin{align*} V_{i,s}\;:\!=\;V_i \cap \left (\bigcap _{j \le s \colon v_iv_j\in F} N_G(u_j)\right ) \end{align*}
\begin{align*} V_{i,s}\;:\!=\;V_i \cap \left (\bigcap _{j \le s \colon v_iv_j\in F} N_G(u_j)\right ) \end{align*}
satisfies the inequality
for all
![]() $i\in [s+1,m]$
.
$i\in [s+1,m]$
.
Proof. For every
![]() $j\in [m]$
let
$j\in [m]$
let
![]() $I_{j}\;:\!=\; \{\ell \in [j+1,m] \colon v_j v_{\ell } \in F\}$
. The proof is by induction on
$I_{j}\;:\!=\; \{\ell \in [j+1,m] \colon v_j v_{\ell } \in F\}$
. The proof is by induction on
![]() $s$
. For the base case
$s$
. For the base case
![]() $s=1$
, first observe that
$s=1$
, first observe that
for all
![]() $j \in I_1$
. Hence we can apply Lemma 2.1 to
$j \in I_1$
. Hence we can apply Lemma 2.1 to
![]() $V_1$
and
$V_1$
and
![]() $V_j$
for all
$V_j$
for all
![]() $j \in I_1$
with
$j \in I_1$
with
![]() $q=2$
to obtain a vertex
$q=2$
to obtain a vertex
![]() $u_1 \in V_1$
such that
$u_1 \in V_1$
such that
![]() $d(u_1, V_j) \ge p |V_j|/2$
for all
$d(u_1, V_j) \ge p |V_j|/2$
for all
![]() $j \in I_1$
. Now suppose that
$j \in I_1$
. Now suppose that
![]() $s \ge 2$
. Apply the induction hypothesis to get
$s \ge 2$
. Apply the induction hypothesis to get
![]() $u_i \in V_i$
for
$u_i \in V_i$
for
![]() $i\in [s-1]$
such that
$i\in [s-1]$
such that
![]() $G[\{u_1, \ldots, u_{s-1}\}]$
contains a copy of
$G[\{u_1, \ldots, u_{s-1}\}]$
contains a copy of
![]() $F[\{v_1, \ldots, v_{s-1}\}]$
and for every
$F[\{v_1, \ldots, v_{s-1}\}]$
and for every
![]() $i\in [s,m]$
the set
$i\in [s,m]$
the set
![]() $U_i \;:\!=\; V_{i, s-1}$
satisfies
$U_i \;:\!=\; V_{i, s-1}$
satisfies
Observe that for every
![]() $j \in I_s$
we have
$j \in I_s$
we have
 \begin{align} |U_s||U_j| \ge \frac{p^{\left |N_{\le s-1}(v_s) \right |} n}{m2^{m}} \cdot \frac{p^{\left |N_{\le s-1}(v_j) \right |} n}{m2^{m}} = \frac{p^{\left |N_{\le s-1}(v_s) \right |+ \left |N_{\le s-1}(v_j) \right |} n^2}{m^22^{2m}} & \ge \frac{p^{2d} n^2}{m^22^{2m}} \notag \\ & \gt 2^m \left (\frac{\alpha }{p} \right )^2. \end{align}
\begin{align} |U_s||U_j| \ge \frac{p^{\left |N_{\le s-1}(v_s) \right |} n}{m2^{m}} \cdot \frac{p^{\left |N_{\le s-1}(v_j) \right |} n}{m2^{m}} = \frac{p^{\left |N_{\le s-1}(v_s) \right |+ \left |N_{\le s-1}(v_j) \right |} n^2}{m^22^{2m}} & \ge \frac{p^{2d} n^2}{m^22^{2m}} \notag \\ & \gt 2^m \left (\frac{\alpha }{p} \right )^2. \end{align}
In the second last inequality we used (b), and in the last inequality we used the assumption that
![]() $\alpha \le p^{d+1}n/(m4^m)$
. So we may apply Lemma 2.1 to
$\alpha \le p^{d+1}n/(m4^m)$
. So we may apply Lemma 2.1 to
![]() $U_s$
and
$U_s$
and
![]() $U_j$
for all
$U_j$
for all
![]() $j \in I_s$
with
$j \in I_s$
with
![]() $q=2$
and obtain
$q=2$
and obtain
![]() $u_{s}\in U_{s}$
such that
$u_{s}\in U_{s}$
such that
![]() $d(u_s, U_j) \ge p|U_j|/2$
for all
$d(u_s, U_j) \ge p|U_j|/2$
for all
![]() $j\in I_s$
. Now by (2), for every
$j\in I_s$
. Now by (2), for every
![]() $i\in I_{s}$
we have
$i\in I_{s}$
we have
On the other hand, by (2), for every
![]() $i\in [s+1, m]\setminus I_{s}$
, we have
$i\in [s+1, m]\setminus I_{s}$
, we have
Finally, it is clear that
![]() $G[\{u_1, u_2, \ldots, u_{s}\}]$
contains a copy of
$G[\{u_1, u_2, \ldots, u_{s}\}]$
contains a copy of
![]() $F[\{v_1, v_2, \ldots, v_{s}\}]$
, so the proof of the claim is complete.
$F[\{v_1, v_2, \ldots, v_{s}\}]$
, so the proof of the claim is complete.
Applying Claim 2.4 with
![]() $s=k-1$
we obtain
$s=k-1$
we obtain
![]() $u_j\in V_j$
for
$u_j\in V_j$
for
![]() $j\in [k-1]$
such that
$j\in [k-1]$
such that
![]() $G[\{u_1, \ldots, u_{k-1}\}]$
contains a copy of
$G[\{u_1, \ldots, u_{k-1}\}]$
contains a copy of
![]() $F_1$
and
$F_1$
and
for all
![]() $i\in [k,m]$
. Now that the first portion of the graph has been embedded, it remains only to embed a forest on the given candidate sets
$i\in [k,m]$
. Now that the first portion of the graph has been embedded, it remains only to embed a forest on the given candidate sets
![]() $X_i\;:\!=\;V_{i,k-1}$
. If we find an embedding
$X_i\;:\!=\;V_{i,k-1}$
. If we find an embedding
![]() $f\colon F_2 \to G$
with
$f\colon F_2 \to G$
with
![]() $f(v_i) \in X_i$
for all
$f(v_i) \in X_i$
for all
![]() $i\in [k,m]$
, then
$i\in [k,m]$
, then
![]() $G[\{u_1,\ldots,u_{k-1}, f(v_k), \ldots, f(v_m)\}]$
contains a copy of
$G[\{u_1,\ldots,u_{k-1}, f(v_k), \ldots, f(v_m)\}]$
contains a copy of
![]() $F$
. Similar to (3), by (c) and Claim 2.4, for every
$F$
. Similar to (3), by (c) and Claim 2.4, for every
![]() $\{v_i,v_j\}\in F_2$
we have
$\{v_i,v_j\}\in F_2$
we have
Applying Lemma 2.3 with
![]() $T = F_2$
and the sets
$T = F_2$
and the sets
![]() $X_{k}, \ldots, X_{m}$
, we know that such an embedding
$X_{k}, \ldots, X_{m}$
, we know that such an embedding
![]() $f$
exists. This completes the proof of Theorem 1.3.
$f$
exists. This completes the proof of Theorem 1.3.
We remark that there are some graphs to which the precise statement of the above theorem cannot be applied in order to get a tight result - for example, odd cycles. However, the proof can be slightly adapted to deal with them. For odd cycles we take
![]() $k = 2$
, so that
$k = 2$
, so that
![]() $F[v_k, \ldots, v_m]$
is a path; this
$F[v_k, \ldots, v_m]$
is a path; this
![]() $F_2$
can then be embedded in a different way than in the general theorem above (see [Reference Conlon, Fox and Zhao17] for more details), in particular, using also the expansion properties of
$F_2$
can then be embedded in a different way than in the general theorem above (see [Reference Conlon, Fox and Zhao17] for more details), in particular, using also the expansion properties of
![]() $(\alpha,p)$
-jumbled graphs.
$(\alpha,p)$
-jumbled graphs.
We now give a further generalisation of Theorem 1.3 where instead of partitioning the graph into two parts which are dealt with separately, we partition the graph into several parts.
For every graph
![]() $F$
on
$F$
on
![]() $m$
vertices, let
$m$
vertices, let
![]() $\hat{d}_{2}(F)$
denote the smallest number
$\hat{d}_{2}(F)$
denote the smallest number
![]() $d$
for which there exists an ordering
$d$
for which there exists an ordering
![]() $v_1,v_2, \ldots, v_m$
of
$v_1,v_2, \ldots, v_m$
of
![]() $V(F)$
such that the following statements hold for some
$V(F)$
such that the following statements hold for some
![]() $\ell \in \mathbb{N}$
and
$\ell \in \mathbb{N}$
and
![]() $1 = k_1 \lt k_2 \lt \cdots \lt k_{\ell } \lt k_{\ell +1} = m$
:
$1 = k_1 \lt k_2 \lt \cdots \lt k_{\ell } \lt k_{\ell +1} = m$
:
-
(i)
 $F[\{v_{k_s}, \ldots, v_{k_{s+1}-1}\}]$
is a forest for all
$F[\{v_{k_s}, \ldots, v_{k_{s+1}-1}\}]$
is a forest for all
 $s\in [\ell ]$
,
$s\in [\ell ]$
, -
(ii) for all edges
 $v_iv_j \in F\setminus \left (\bigcup _{s=1}^{\ell }F[\{v_{k_s}, \ldots, v_{k_{s+1}-1}\}]\right )$
with
$v_iv_j \in F\setminus \left (\bigcup _{s=1}^{\ell }F[\{v_{k_s}, \ldots, v_{k_{s+1}-1}\}]\right )$
with
 $i\lt j$
, we have
$i\lt j$
, we have
 $N_{\lt i}(v_i) + N_{\lt i}(v_j) \leq 2d$
, and
$N_{\lt i}(v_i) + N_{\lt i}(v_j) \leq 2d$
, and -
(iii) for all
 $s\in [\ell ]$
and for all edges
$s\in [\ell ]$
and for all edges
 $v_iv_j \in F[\{v_{k_s}, \ldots, v_{k_{s+1}-1}\}]$
, we have
$v_iv_j \in F[\{v_{k_s}, \ldots, v_{k_{s+1}-1}\}]$
, we have
 $N_{\lt k_s}(v_i) + N_{\lt k_s}(v_j) \leq 2d$
.
$N_{\lt k_s}(v_i) + N_{\lt k_s}(v_j) \leq 2d$
.
It is clear that
![]() $\hat{d}_{2}(F) \le d_{2}(F)$
since in the definition of
$\hat{d}_{2}(F) \le d_{2}(F)$
since in the definition of
![]() $d_{2}(F)$
we always let
$d_{2}(F)$
we always let
![]() $\ell =m-1$
and
$\ell =m-1$
and
![]() $k_i = i$
for all
$k_i = i$
for all
![]() $i\in [m]$
.
$i\in [m]$
.
Theorem 2.5.
For every graph
![]() $F$
we have
$F$
we have
![]() $\mathrm{exp}(F) \leq 1 - \frac{1}{2\hat{d}_{2}(F)+1}$
.
$\mathrm{exp}(F) \leq 1 - \frac{1}{2\hat{d}_{2}(F)+1}$
.
Remark 4. One can extend Theorem 2.5 to get a counting result for
![]() $F$
in pseudorandom graphs that improves Theorem 1.14 in [Reference Conlon, Fox and Zhao17] (by replacing
$F$
in pseudorandom graphs that improves Theorem 1.14 in [Reference Conlon, Fox and Zhao17] (by replacing
![]() $d_2(F)$
there with
$d_2(F)$
there with
![]() $\hat{d}_2(F)$
here). This could result in some improvements for the corresponding Turán and Ramsey problems in pseudorandom graphs (see Theorems 1.4, 1.5, and 1.6 in [Reference Conlon, Fox and Zhao17]).
$\hat{d}_2(F)$
here). This could result in some improvements for the corresponding Turán and Ramsey problems in pseudorandom graphs (see Theorems 1.4, 1.5, and 1.6 in [Reference Conlon, Fox and Zhao17]).
3.
 $\{K_{2,3}, K_3\}$
-free pseudorandom graphs
$\{K_{2,3}, K_3\}$
-free pseudorandom graphs
In this section we present a construction of
![]() $\{K_{2,3}, K_3\}$
-free pseudorandom graphs thereby proving Theorem 1.5.
$\{K_{2,3}, K_3\}$
-free pseudorandom graphs thereby proving Theorem 1.5.
Suppose that
![]() $F$
is a finite group and
$F$
is a finite group and
![]() $S \subset H$
is a symmetric subset, i.e.
$S \subset H$
is a symmetric subset, i.e.
![]() $S = S^{-1}$
. Then the Cayley graph
$S = S^{-1}$
. Then the Cayley graph
![]() $\mathrm{Cay}(H,S)$
is a graph on
$\mathrm{Cay}(H,S)$
is a graph on
![]() $F$
with edge set
$F$
with edge set
The spectrum, i.e. the eigenvalues of the adjacency matrix, of a Cayley graph can be represented by the characters of
![]() $F$
(see e.g. [Reference Babai6, Reference Lovász29]). For our purpose, we only need the following result for the case that
$F$
(see e.g. [Reference Babai6, Reference Lovász29]). For our purpose, we only need the following result for the case that
![]() $F$
is an abelian group.
$F$
is an abelian group.
Recall that an abelian group
![]() $H$
can be represented as
$H$
can be represented as
![]() $H = \bigoplus _{i=1}^{k}\mathbb{Z}_{n_i}$
for some integers
$H = \bigoplus _{i=1}^{k}\mathbb{Z}_{n_i}$
for some integers
![]() $k$
and
$k$
and
![]() $n_1, \ldots, n_{k}$
. For abelian groups we have a simple description of all the characters. For each
$n_1, \ldots, n_{k}$
. For abelian groups we have a simple description of all the characters. For each
![]() $\textbf{a} = (a_1, \ldots, a_{k}) \in \bigoplus _{i=1}^{k}\mathbb{Z}_{n_i}$
we have a character
$\textbf{a} = (a_1, \ldots, a_{k}) \in \bigoplus _{i=1}^{k}\mathbb{Z}_{n_i}$
we have a character
![]() $\psi _{\textbf{a}} \colon H\to \mathbb{C}$
defined by
$\psi _{\textbf{a}} \colon H\to \mathbb{C}$
defined by
 \begin{align*} \psi _{\textbf{a}}(h_1, \ldots, h_k) = \prod _{i=1}^{k} \omega _{n_i}^{a_i h_i}, \end{align*}
\begin{align*} \psi _{\textbf{a}}(h_1, \ldots, h_k) = \prod _{i=1}^{k} \omega _{n_i}^{a_i h_i}, \end{align*}
where
![]() $\omega _t = e^{2\pi i/t}$
.
$\omega _t = e^{2\pi i/t}$
.
Lemma 3.1 (see e.g. [Reference Babai6, Reference Lovász29]). Suppose that
![]() $H = \bigoplus _{i=1}^{k}\mathbb{Z}_{n_i}$
is an abelian group. Then the spectrum of the Cayley graph
$H = \bigoplus _{i=1}^{k}\mathbb{Z}_{n_i}$
is an abelian group. Then the spectrum of the Cayley graph
![]() $\mathrm{Cay}(H,S)$
is
$\mathrm{Cay}(H,S)$
is
 \begin{align*} \left \{\sum _{\textbf{s}\in S}\psi _{\textbf{a}}(\textbf{s}) \colon \textbf{a}\in H \right \}. \end{align*}
\begin{align*} \left \{\sum _{\textbf{s}\in S}\psi _{\textbf{a}}(\textbf{s}) \colon \textbf{a}\in H \right \}. \end{align*}
Our main result is as follows.
Theorem 3.2.
Suppose that
![]() $p\neq 3$
is a prime number,
$p\neq 3$
is a prime number,
![]() $H = \mathbb{Z}_{p}^2$
, and
$H = \mathbb{Z}_{p}^2$
, and
Then
![]() $\mathrm{Cay}(H,S)$
is a
$\mathrm{Cay}(H,S)$
is a
![]() $\{K_{3}, K_{2,3}\}$
-free
$\{K_{3}, K_{2,3}\}$
-free
![]() $(n,d,\lambda )$
-graph with
$(n,d,\lambda )$
-graph with
![]() $n = p^2$
,
$n = p^2$
,
![]() $d = p-1$
, and
$d = p-1$
, and
![]() $\lambda \le 2 \sqrt{p}+1$
.
$\lambda \le 2 \sqrt{p}+1$
.
We will use the following well known estimate of Weil in the proof of Theorem 3.2.
Recall that the order of a character
![]() $\chi$
is the smallest positive integer
$\chi$
is the smallest positive integer
![]() $d$
such that
$d$
such that
![]() $\chi ^d = \chi _0$
, where
$\chi ^d = \chi _0$
, where
![]() $\chi _0$
is the trivial character.
$\chi _0$
is the trivial character.
Theorem 3.3 (see e.g. [Reference Bollobás11, Theorem 13.3]). Let
![]() $\chi$
be a character of order
$\chi$
be a character of order
![]() $d \gt 1$
. Suppose that
$d \gt 1$
. Suppose that
![]() $f(X)\in \mathbb{F}[X]$
has precisely
$f(X)\in \mathbb{F}[X]$
has precisely
![]() $m$
distinct zeros and it is not a
$m$
distinct zeros and it is not a
![]() $d$
th power, that is
$d$
th power, that is
![]() $f(X)$
is not the form
$f(X)$
is not the form
![]() $c\left (g(X)\right )^{d}$
, where
$c\left (g(X)\right )^{d}$
, where
![]() $c\in \mathbb{F}$
and
$c\in \mathbb{F}$
and
![]() $g(X)\in \mathbb{F}[X]$
. Then
$g(X)\in \mathbb{F}[X]$
. Then
 \begin{align*} \left | \sum _{x\in \mathbb{F}}\chi \left (f(x)\right ) \right | \le (m-1)\sqrt{p}. \end{align*}
\begin{align*} \left | \sum _{x\in \mathbb{F}}\chi \left (f(x)\right ) \right | \le (m-1)\sqrt{p}. \end{align*}
Proof of Theorem
3.2
. Let
![]() $G = \mathrm{Cay}(H,S)$
. Let
$G = \mathrm{Cay}(H,S)$
. Let
![]() $n=p^2$
. It is clear that the number of vertices in
$n=p^2$
. It is clear that the number of vertices in
![]() $G$
is
$G$
is
![]() $n$
, and it follows from the definition of Cayley graphs that
$n$
, and it follows from the definition of Cayley graphs that
![]() $G$
is
$G$
is
![]() $|S|$
-regular. Let
$|S|$
-regular. Let
![]() $\lambda _1 \ge \cdots \ge \lambda _n$
be the eigenvalues of the adjacency matrix
$\lambda _1 \ge \cdots \ge \lambda _n$
be the eigenvalues of the adjacency matrix
![]() $A_{G}$
of
$A_{G}$
of
![]() $G$
. Since
$G$
. Since
![]() $G$
is regular, we have
$G$
is regular, we have
![]() $\lambda _1 = |S| = p-1$
.
$\lambda _1 = |S| = p-1$
.
First we prove that
![]() $G$
is
$G$
is
![]() $K_3$
-free. Suppose to the contrary that there exist three vertices
$K_3$
-free. Suppose to the contrary that there exist three vertices
![]() $\textbf{u}, \textbf{v}, \textbf{w} \in \mathbb{Z}_{p}^2$
that form a copy of
$\textbf{u}, \textbf{v}, \textbf{w} \in \mathbb{Z}_{p}^2$
that form a copy of
![]() $K_3$
in
$K_3$
in
![]() $G$
. Assume that
$G$
. Assume that
![]() $\textbf{v}-\textbf{u} = (a,a^3)$
,
$\textbf{v}-\textbf{u} = (a,a^3)$
,
![]() $\textbf{w}-\textbf{v}=(b,b^3)$
, and
$\textbf{w}-\textbf{v}=(b,b^3)$
, and
![]() $\textbf{u}-\textbf{w}=(c,c^3)$
. Then
$\textbf{u}-\textbf{w}=(c,c^3)$
. Then
Therefore,
Since
![]() $p\neq 3$
, we must have
$p\neq 3$
, we must have
![]() $0\in \{a,b,c\}$
, a contradiction.
$0\in \{a,b,c\}$
, a contradiction.
Next we prove that
![]() $G$
is
$G$
is
![]() $K_{2,3}$
-free. It is equivalent to show that every pair of vertices
$K_{2,3}$
-free. It is equivalent to show that every pair of vertices
![]() $\{ \textbf{u}, \textbf{v} \} \subset \mathbb{Z}_{p}^2$
has at most two common neighbours. Let
$\{ \textbf{u}, \textbf{v} \} \subset \mathbb{Z}_{p}^2$
has at most two common neighbours. Let
![]() $(a,b) = \textbf{u} - \textbf{v}$
. A common neighbour of
$(a,b) = \textbf{u} - \textbf{v}$
. A common neighbour of
![]() $\textbf{u}$
and
$\textbf{u}$
and
![]() $\textbf{v}$
implies that there exist
$\textbf{v}$
implies that there exist
![]() $x,y\in \mathbb{Z}_{p}\setminus \{0\}$
such that
$x,y\in \mathbb{Z}_{p}\setminus \{0\}$
such that
These two equations imply that
![]() $(x+a)^3 = x^3+b$
, which simplifies to
$(x+a)^3 = x^3+b$
, which simplifies to
![]() $3ax^2+3a^2x+a^3-b=0$
. Since
$3ax^2+3a^2x+a^3-b=0$
. Since
![]() $(a,b) \ne (0,0)$
and
$(a,b) \ne (0,0)$
and
![]() $p \ne 3$
, this quadratic equation in
$p \ne 3$
, this quadratic equation in
![]() $x$
has at most two solutions in
$x$
has at most two solutions in
![]() $\mathbb{Z}_{p}\setminus \{0\}$
. Therefore,
$\mathbb{Z}_{p}\setminus \{0\}$
. Therefore,
![]() $\textbf{u}$
and
$\textbf{u}$
and
![]() $\textbf{v}$
have at most two common neighbours.
$\textbf{v}$
have at most two common neighbours.
Finally, we prove that
![]() $|\lambda _i| \le 2\sqrt{p}$
for all
$|\lambda _i| \le 2\sqrt{p}$
for all
![]() $i\in [2,n]$
. By Lemma 3.1, for every
$i\in [2,n]$
. By Lemma 3.1, for every
![]() $i\in [n]$
there exists
$i\in [n]$
there exists
![]() $(a_1, a_2) \in \mathbb{Z}_{p}^2$
such that
$(a_1, a_2) \in \mathbb{Z}_{p}^2$
such that
 \begin{align*} \lambda _i = \lambda _{(a_1,a_2)} = \sum _{\textbf{s}\in S}\varphi _{(a_1,a_2)}(\textbf{s}) = \sum _{x=1}^{p-1}\omega _{p}^{a_1x+a_2x^3} \end{align*}
\begin{align*} \lambda _i = \lambda _{(a_1,a_2)} = \sum _{\textbf{s}\in S}\varphi _{(a_1,a_2)}(\textbf{s}) = \sum _{x=1}^{p-1}\omega _{p}^{a_1x+a_2x^3} \end{align*}
If
![]() $(a_1,a_2) = (0,0)$
, then
$(a_1,a_2) = (0,0)$
, then
![]() $\lambda _{(a_1,a_2)} = |S| = p-1$
, and this corresponds to
$\lambda _{(a_1,a_2)} = |S| = p-1$
, and this corresponds to
![]() $\lambda _1$
. So we may assume that
$\lambda _1$
. So we may assume that
![]() $(a_1,a_2) \neq (0,0)$
.
$(a_1,a_2) \neq (0,0)$
.
First, it is easy to see that the character
![]() $\chi \colon \mathbb{Z}_p \to \mathbb{C}^{\times }$
defined by
$\chi \colon \mathbb{Z}_p \to \mathbb{C}^{\times }$
defined by
![]() $\chi (\alpha ) = \omega _{p}^{\alpha }$
for all
$\chi (\alpha ) = \omega _{p}^{\alpha }$
for all
![]() $\alpha \in \mathbb{Z}_p$
has order
$\alpha \in \mathbb{Z}_p$
has order
![]() $p$
. On the other hand, since
$p$
. On the other hand, since
![]() $(a_1,a_2) \neq (0,0)$
and
$(a_1,a_2) \neq (0,0)$
and
![]() $p\neq 3$
, the polynomial
$p\neq 3$
, the polynomial
![]() $f(X) = a_1 X + a_2 X^3$
is not of the form
$f(X) = a_1 X + a_2 X^3$
is not of the form
![]() $c\left (g(X)\right )^p$
for any
$c\left (g(X)\right )^p$
for any
![]() $c\in \mathbb{Z}_p$
and for any polynomial
$c\in \mathbb{Z}_p$
and for any polynomial
![]() $g(X)$
. Therefore, it follows from Theorem 3.3 that
$g(X)$
. Therefore, it follows from Theorem 3.3 that
 \begin{align*} \left |\sum _{x=1}^{p-1}\omega _{p}^{a_1x + a_2x^3} \right | = \left |\sum _{x=0}^{p-1}\omega _{p}^{a_1x + a_2x^3} - 1\right | \le \left |\sum _{x=0}^{p-1}\omega _{p}^{a_1x + a_2x^3}\right |+1 \le 2\sqrt{p}+1. \end{align*}
\begin{align*} \left |\sum _{x=1}^{p-1}\omega _{p}^{a_1x + a_2x^3} \right | = \left |\sum _{x=0}^{p-1}\omega _{p}^{a_1x + a_2x^3} - 1\right | \le \left |\sum _{x=0}^{p-1}\omega _{p}^{a_1x + a_2x^3}\right |+1 \le 2\sqrt{p}+1. \end{align*}
This implies that
![]() $|\lambda _i| \le 2\sqrt{p}+1$
for all
$|\lambda _i| \le 2\sqrt{p}+1$
for all
![]() $i\in [2, n]$
, and hence completes the proof of Theorem 3.2.
$i\in [2, n]$
, and hence completes the proof of Theorem 3.2.
4.
 $K_t$
-free pseudorandom graphs
$K_t$
-free pseudorandom graphs
In this section, we present a construction that is isomorphic to the construction of Bishnoi, Ihringer, and Pepe [Reference Bishnoi, Ihringer and Pepe10], and provide a new proof of Theorem 1.1. For simplicity, we omit the short proof of the
![]() $(p,\alpha )$
-jumbledness part (which can be found in [Reference Alon and Krivelevich4, p. 220] and [Reference Bishnoi, Ihringer and Pepe10, Theorem 9]) and focus only on the
$(p,\alpha )$
-jumbledness part (which can be found in [Reference Alon and Krivelevich4, p. 220] and [Reference Bishnoi, Ihringer and Pepe10, Theorem 9]) and focus only on the
![]() $K_t$
-freeness part.
$K_t$
-freeness part.
Denote by
![]() $\mathrm{PG}(t-1,q)$
the
$\mathrm{PG}(t-1,q)$
the
![]() $(t-1)$
-dimensional projective space over
$(t-1)$
-dimensional projective space over
![]() $\mathbb{F}_{q}$
, i.e.
$\mathbb{F}_{q}$
, i.e.
![]() $\mathrm{PG}(t-1,q) = \mathbb{F}_{q}^{t}/{\sim }$
, where two vectors
$\mathrm{PG}(t-1,q) = \mathbb{F}_{q}^{t}/{\sim }$
, where two vectors
![]() $\textbf{x}, \textbf{y} \in \mathbb{F}_{q}^{t}$
are equivalent under
$\textbf{x}, \textbf{y} \in \mathbb{F}_{q}^{t}$
are equivalent under
![]() $\sim$
if there exists a non-zero element
$\sim$
if there exists a non-zero element
![]() $a\in \mathbb{F}_{q}$
such that
$a\in \mathbb{F}_{q}$
such that
![]() $\textbf{x} = a \textbf{y}$
. For a vector
$\textbf{x} = a \textbf{y}$
. For a vector
![]() $\textbf{x} \in \mathbb{F}_{q}^{t}$
we use
$\textbf{x} \in \mathbb{F}_{q}^{t}$
we use
![]() $[\![\textbf{x}]\!]$
to denote its equivalence class in
$[\![\textbf{x}]\!]$
to denote its equivalence class in
![]() $\mathbb{F}_{q}^{t}/{\sim }$
. It is easy to see that the number of points in
$\mathbb{F}_{q}^{t}/{\sim }$
. It is easy to see that the number of points in
![]() $\mathrm{PG}(t-1,q)$
is
$\mathrm{PG}(t-1,q)$
is
![]() $\frac{q^t-1}{q-1} = (1+o(1))q^{t-1}$
. Recall that the dot-product
$\frac{q^t-1}{q-1} = (1+o(1))q^{t-1}$
. Recall that the dot-product
![]() $ \textbf{x}\cdot \textbf{y}$
of two vectors
$ \textbf{x}\cdot \textbf{y}$
of two vectors
![]() $\textbf{x}, \textbf{y} \in \mathbb{F}_{q}^{t}$
is defined as
$\textbf{x}, \textbf{y} \in \mathbb{F}_{q}^{t}$
is defined as
![]() $\textbf{x}\cdot \textbf{y} = \sum _{i=1}^{t}x_iy_i$
. A point
$\textbf{x}\cdot \textbf{y} = \sum _{i=1}^{t}x_iy_i$
. A point
![]() $\textbf{x}=(x_1,\ldots,x_t) \in \mathbb{F}_{q}^{t}$
is called
$\textbf{x}=(x_1,\ldots,x_t) \in \mathbb{F}_{q}^{t}$
is called
-
• absolute if
 $\textbf{x}\cdot \textbf{x} = 0$
,
$\textbf{x}\cdot \textbf{x} = 0$
, -
• square if
 $\textbf{x}\cdot \textbf{x} = a^2$
for some
$\textbf{x}\cdot \textbf{x} = a^2$
for some
 $a\in \mathbb{F}_{q}$
,
$a\in \mathbb{F}_{q}$
, -
• non-square if
 $\textbf{x}\cdot \textbf{x} \neq a^2$
for all
$\textbf{x}\cdot \textbf{x} \neq a^2$
for all
 $a\in \mathbb{F}_{q}$
,
$a\in \mathbb{F}_{q}$
,
We use
![]() $X_{0}(t,q), X_{\Box }(t,q), X_{\boxtimes }(t,q)$
to denote the collection of all absolute points, square points, and non-square points in
$X_{0}(t,q), X_{\Box }(t,q), X_{\boxtimes }(t,q)$
to denote the collection of all absolute points, square points, and non-square points in
![]() $\mathbb{F}_{q}^{t}$
, respectively. If
$\mathbb{F}_{q}^{t}$
, respectively. If
![]() $t$
and
$t$
and
![]() $q$
are clear from the context, we will omit them and use
$q$
are clear from the context, we will omit them and use
![]() $X_{0}, X_{\Box }, X_{\boxtimes }$
for simplicity. It is easy to see from the definition that if
$X_{0}, X_{\Box }, X_{\boxtimes }$
for simplicity. It is easy to see from the definition that if
![]() $\textbf{x} \in X_{0}$
,
$\textbf{x} \in X_{0}$
,
![]() $\textbf{x} \in X_{\Box }$
, or
$\textbf{x} \in X_{\Box }$
, or
![]() $\textbf{x} \in X_{\boxtimes }$
, then
$\textbf{x} \in X_{\boxtimes }$
, then
![]() $[\![\textbf{x}]\!] \subset X_{0}$
,
$[\![\textbf{x}]\!] \subset X_{0}$
,
![]() $[\![\textbf{x}]\!] \subset X_{\Box }$
, or
$[\![\textbf{x}]\!] \subset X_{\Box }$
, or
![]() $[\![\textbf{x}]\!] \subset X_{\boxtimes }$
, respectively.
$[\![\textbf{x}]\!] \subset X_{\boxtimes }$
, respectively.
Recall that a character of a group
![]() $H$
is a homomorphism
$H$
is a homomorphism
![]() $\psi \colon H \to \mathbb{C}^{\times }$
, and the quadratic character
$\psi \colon H \to \mathbb{C}^{\times }$
, and the quadratic character
![]() $\chi (\cdot )$
of
$\chi (\cdot )$
of
![]() $\mathbb{F}_{q}$
is defined as
$\mathbb{F}_{q}$
is defined as
 \begin{align*} \chi (x) = \begin{cases} 0, & \text{if } x = 0, \\ 1, & \text{if } x \text{ is a square}, \\ -1, & \text{if } x \text{ is a non-square}. \end{cases} \end{align*}
\begin{align*} \chi (x) = \begin{cases} 0, & \text{if } x = 0, \\ 1, & \text{if } x \text{ is a square}, \\ -1, & \text{if } x \text{ is a non-square}. \end{cases} \end{align*}
Let
![]() $\mathrm{AK}(t-1,q)$
be the graph whose vertices are non-absolute points of
$\mathrm{AK}(t-1,q)$
be the graph whose vertices are non-absolute points of
![]() $\mathrm{PG}(t-1,q)$
and two vertices
$\mathrm{PG}(t-1,q)$
and two vertices
![]() $[\![\textbf{x}]\!]$
and
$[\![\textbf{x}]\!]$
and
![]() $[\![\textbf{y}]\!]$
are adjacent iff
$[\![\textbf{y}]\!]$
are adjacent iff
![]() $\textbf{x}\cdot \textbf{y} = 0$
. Note that
$\textbf{x}\cdot \textbf{y} = 0$
. Note that
![]() $\mathrm{AK}(2,q)$
is just the Erdős–Renyi graph. In [Reference Alon and Krivelevich4], Alon and Krivelevich proved that
$\mathrm{AK}(2,q)$
is just the Erdős–Renyi graph. In [Reference Alon and Krivelevich4], Alon and Krivelevich proved that
![]() $\mathrm{AK}(t-1,q)$
is a
$\mathrm{AK}(t-1,q)$
is a
![]() $K_{t+1}$
-free
$K_{t+1}$
-free
![]() $(n,d,\lambda )$
-graph with
$(n,d,\lambda )$
-graph with
![]() $n = (1+o(1))q^{t-1}$
,
$n = (1+o(1))q^{t-1}$
,
![]() $d = \Theta (n^{1-\frac{1}{t-1}})$
, and
$d = \Theta (n^{1-\frac{1}{t-1}})$
, and
![]() $\lambda = \Theta (\sqrt{d})$
.
$\lambda = \Theta (\sqrt{d})$
.
Parsons [Reference Parsons33] proved that for
![]() $q$
odd, the induced subgraph of
$q$
odd, the induced subgraph of
![]() $\mathrm{AK}(2,q)$
on
$\mathrm{AK}(2,q)$
on
![]() $X_{\boxtimes }/{\sim }$
is
$X_{\boxtimes }/{\sim }$
is
![]() $K_3$
-free. Indeed, suppose to the contrary that there exist three distinct points
$K_3$
-free. Indeed, suppose to the contrary that there exist three distinct points
![]() $[\![\textbf{x}_1]\!], [\![\textbf{x}_2]\!], [\![\textbf{x}_3]\!] \in X_{\boxtimes }/{\sim }$
that induce a copy of
$[\![\textbf{x}_1]\!], [\![\textbf{x}_2]\!], [\![\textbf{x}_3]\!] \in X_{\boxtimes }/{\sim }$
that induce a copy of
![]() $K_3$
in
$K_3$
in
![]() $\mathrm{AK}(2,q)$
. Then
$\mathrm{AK}(2,q)$
. Then
![]() $\textbf{x}_1, \textbf{x}_2, \textbf{x}_3$
are pairwise orthogonal, which means that there exists a non-zero element
$\textbf{x}_1, \textbf{x}_2, \textbf{x}_3$
are pairwise orthogonal, which means that there exists a non-zero element
![]() $a\in \mathbb{F}_{q}$
such that
$a\in \mathbb{F}_{q}$
such that
![]() $\textbf{x}_3 = a \textbf{x}_1 \times \textbf{x}_2$
, where
$\textbf{x}_3 = a \textbf{x}_1 \times \textbf{x}_2$
, where
![]() $\textbf{x}_1 \times \textbf{x}_2$
is the cross-product of
$\textbf{x}_1 \times \textbf{x}_2$
is the cross-product of
![]() $\textbf{x}_1$
and
$\textbf{x}_1$
and
![]() $\textbf{x}_2$
. Therefore, we have
$\textbf{x}_2$
. Therefore, we have
where in the last equality we used the fact that
![]() $\textbf{x}_1 \cdot \textbf{x}_{2} = 0$
. Applying the quadratic character
$\textbf{x}_1 \cdot \textbf{x}_{2} = 0$
. Applying the quadratic character
![]() $\chi (\cdot )$
to both sides of the equation above we obtain
$\chi (\cdot )$
to both sides of the equation above we obtain
a contradiction. Therefore, the induced subgraph of
![]() $\mathrm{AK}(2,q)$
on
$\mathrm{AK}(2,q)$
on
![]() $X_{\boxtimes }/{\sim }$
is
$X_{\boxtimes }/{\sim }$
is
![]() $K_3$
-free.
$K_3$
-free.
Our aim in this section is to extend Parsons’ proof to the following general symmetric bilinear forms on
![]() $\mathbb{F}^{t} \times \mathbb{F}^{t}$
for all
$\mathbb{F}^{t} \times \mathbb{F}^{t}$
for all
![]() $t \ge 4$
.
$t \ge 4$
.
Fix a non-degenerate symmetric bilinear form
![]() $B \colon \mathbb{F}^{t} \times \mathbb{F}^{t} \to \mathbb{F}$
such that
$B \colon \mathbb{F}^{t} \times \mathbb{F}^{t} \to \mathbb{F}$
such that
where
![]() $a_1, \ldots, a_t$
are non-zero elements in
$a_1, \ldots, a_t$
are non-zero elements in
![]() $\mathbb{F}_{q}$
. A point
$\mathbb{F}_{q}$
. A point
![]() $\textbf{x}=(x_1,\ldots,x_t) \in \mathbb{F}_{q}^{t}$
is called
$\textbf{x}=(x_1,\ldots,x_t) \in \mathbb{F}_{q}^{t}$
is called
-
•
 $B$
-absolute if
$B$
-absolute if
 $B(\textbf{x},\textbf{x}) = 0$
,
$B(\textbf{x},\textbf{x}) = 0$
, -
•
 $B$
-square if
$B$
-square if
 $B(\textbf{x},\textbf{x}) = a^2$
for some
$B(\textbf{x},\textbf{x}) = a^2$
for some
 $a\in \mathbb{F}_{q}$
,
$a\in \mathbb{F}_{q}$
, -
• non-
 $B$
-square if
$B$
-square if
 $B(\textbf{x},\textbf{x}) \neq a^2$
for all
$B(\textbf{x},\textbf{x}) \neq a^2$
for all
 $a\in \mathbb{F}_{q}$
,
$a\in \mathbb{F}_{q}$
,
We use
![]() $X_{B,0}(t,q), X_{B,\Box }(t,q), X_{B,\boxtimes }(t,q)$
to denote the collection of all
$X_{B,0}(t,q), X_{B,\Box }(t,q), X_{B,\boxtimes }(t,q)$
to denote the collection of all
![]() $B$
-absolute points,
$B$
-absolute points,
![]() $B$
-square points, and non-
$B$
-square points, and non-
![]() $B$
-square points in
$B$
-square points in
![]() $\mathbb{F}_{q}^{t}$
, respectively. Similarly, let
$\mathbb{F}_{q}^{t}$
, respectively. Similarly, let
![]() $\mathrm{AK}_{B}(t-1,q)$
be the graph whose vertices are non-
$\mathrm{AK}_{B}(t-1,q)$
be the graph whose vertices are non-
![]() $B$
-absolute points of
$B$
-absolute points of
![]() $\mathrm{PG}(t-1,q)$
and two vertices
$\mathrm{PG}(t-1,q)$
and two vertices
![]() $[\![\textbf{x}]\!]$
and
$[\![\textbf{x}]\!]$
and
![]() $[\![\textbf{y}]\!]$
are adjacent iff
$[\![\textbf{y}]\!]$
are adjacent iff
![]() $B(\textbf{x}, \textbf{y}) = 0$
.
$B(\textbf{x}, \textbf{y}) = 0$
.
The cross-product used by Parsons [Reference Parsons33] in
![]() $\mathbb{F}_{q}^{3}$
can be extended to
$\mathbb{F}_{q}^{3}$
can be extended to
![]() $t$
-dimensional space
$t$
-dimensional space
![]() $\mathbb{F}_{q}^{t}$
under the general symmetric bilinear form defined by (4) for every
$\mathbb{F}_{q}^{t}$
under the general symmetric bilinear form defined by (4) for every
![]() $t\ge 4$
by letting
$t\ge 4$
by letting
Here
![]() ${\star } \colon \bigwedge ^{t-1} \mathbb{F}_{q}^{t} \to \bigwedge ^{1} \mathbb{F}_{q}^{t}$
is the Hodge star map defined by
${\star } \colon \bigwedge ^{t-1} \mathbb{F}_{q}^{t} \to \bigwedge ^{1} \mathbb{F}_{q}^{t}$
is the Hodge star map defined by
where
![]() $\textbf{e}_1 \;:\!=\; (1, 0, \ldots, 0), \cdots, \textbf{e}_t \;:\!=\; (0, \ldots, 0, 1)$
(see [Reference Brown and Gray14, Section 3]). We refer the reader to [Reference Dittmer18, Reference Spivak35] for more discussions on this definition. Here we only list some basic properties of the cross-product defined above.
$\textbf{e}_1 \;:\!=\; (1, 0, \ldots, 0), \cdots, \textbf{e}_t \;:\!=\; (0, \ldots, 0, 1)$
(see [Reference Brown and Gray14, Section 3]). We refer the reader to [Reference Dittmer18, Reference Spivak35] for more discussions on this definition. Here we only list some basic properties of the cross-product defined above.
Fact 4.1 (see e.g. [Reference Dittmer18]). Suppose that
![]() $\textbf{x}_1, \ldots, \textbf{x}_{t-1} \in \mathbb{F}_{q}^t$
are
$\textbf{x}_1, \ldots, \textbf{x}_{t-1} \in \mathbb{F}_{q}^t$
are
![]() $t-1$
vectors. Then
$t-1$
vectors. Then
-
(i)
 $\textbf{x}_1 \times \cdots \times \textbf{x}_{t-1}$
is skew-symmetric and linear in each
$\textbf{x}_1 \times \cdots \times \textbf{x}_{t-1}$
is skew-symmetric and linear in each
 $\textbf{x}_i$
,
$\textbf{x}_i$
, -
(ii)
 $\textbf{x}_1 \times \cdots \times \textbf{x}_{t-1}$
is a vector that is orthogonal to each of
$\textbf{x}_1 \times \cdots \times \textbf{x}_{t-1}$
is a vector that is orthogonal to each of
 $\textbf{x}_1, \ldots, \textbf{x}_{t-1}$
,
$\textbf{x}_1, \ldots, \textbf{x}_{t-1}$
, -
(iii)
 $\textbf{x}_1 \times \cdots \times \textbf{x}_{t-1} = 0$
iff
$\textbf{x}_1 \times \cdots \times \textbf{x}_{t-1} = 0$
iff
 $\textbf{x}_1, \ldots, \textbf{x}_{t-1}$
are linearly dependent.
$\textbf{x}_1, \ldots, \textbf{x}_{t-1}$
are linearly dependent.
A proof of the following theorem for the case where
![]() $B(\cdot, \cdot )$
is the dot-product can be found in [Reference Dittmer18, Reference Shaw and Yeadon34]. In fact, their proofFootnote 2 works for the symmetric bilinear form defined by (4) (see [Reference Shaw and Yeadon34, Proof C] and [Reference Dittmer18, p. 888] for more details).
$B(\cdot, \cdot )$
is the dot-product can be found in [Reference Dittmer18, Reference Shaw and Yeadon34]. In fact, their proofFootnote 2 works for the symmetric bilinear form defined by (4) (see [Reference Shaw and Yeadon34, Proof C] and [Reference Dittmer18, p. 888] for more details).
Theorem 4.2 (see e.g. [Reference Dittmer18]). Let
![]() $\textbf{x}_1,\ldots,\textbf{x}_{t-1}, \textbf{y}_1,\ldots, \textbf{y}_{t-1}\in \mathbb{F}_{q}^t$
and
$\textbf{x}_1,\ldots,\textbf{x}_{t-1}, \textbf{y}_1,\ldots, \textbf{y}_{t-1}\in \mathbb{F}_{q}^t$
and
![]() $B \colon \mathbb{F}^{t} \times \mathbb{F}^{t} \to \mathbb{F}$
be the non-degenerate symmetric bilinear form defined by (4). Then
$B \colon \mathbb{F}^{t} \times \mathbb{F}^{t} \to \mathbb{F}$
be the non-degenerate symmetric bilinear form defined by (4). Then
 \begin{align*} B(\textbf{x}_1\times \cdots \times \textbf{x}_{t-1},\ \textbf{y}_1\times \cdots \times \textbf{y}_{t-1}) & =\prod _{i\in [t]}a_i \cdot \mathrm{det} \begin{bmatrix} B(\textbf{x}_1, \textbf{y}_1) & & \dots & & B(\textbf{x}_1, \textbf{y}_{t-1}) \\ \vdots && \ddots && \vdots \\ B(\textbf{x}_{t-1}, \textbf{y}_1) && \dots && B(\textbf{x}_{t-1}, \textbf{y}_{t-1}) \end{bmatrix}. \end{align*}
\begin{align*} B(\textbf{x}_1\times \cdots \times \textbf{x}_{t-1},\ \textbf{y}_1\times \cdots \times \textbf{y}_{t-1}) & =\prod _{i\in [t]}a_i \cdot \mathrm{det} \begin{bmatrix} B(\textbf{x}_1, \textbf{y}_1) & & \dots & & B(\textbf{x}_1, \textbf{y}_{t-1}) \\ \vdots && \ddots && \vdots \\ B(\textbf{x}_{t-1}, \textbf{y}_1) && \dots && B(\textbf{x}_{t-1}, \textbf{y}_{t-1}) \end{bmatrix}. \end{align*}
Our main result in this section is as follows.
Theorem 4.3.
Suppose that
![]() $q$
is an odd prime power,
$q$
is an odd prime power,
![]() $t\ge 3$
is an integer, and
$t\ge 3$
is an integer, and
![]() $B \colon \mathbb{F}^{t} \times \mathbb{F}^{t} \to \mathbb{F}$
is the non-degenerate symmetric bilinear form defined by (4). Then the following statements hold.
$B \colon \mathbb{F}^{t} \times \mathbb{F}^{t} \to \mathbb{F}$
is the non-degenerate symmetric bilinear form defined by (4). Then the following statements hold.
-
(i) If
 $t$
is odd and
$t$
is odd and
 $\prod _{i\in [t]}a_i$
is a square, then the induced subgraph of
$\prod _{i\in [t]}a_i$
is a square, then the induced subgraph of
 $\mathrm{AK}_{B}(t-1,q)$
on
$\mathrm{AK}_{B}(t-1,q)$
on
 $X_{B,\boxtimes }/{\sim }$
is a
$X_{B,\boxtimes }/{\sim }$
is a
 $K_{t}$
-free.
$K_{t}$
-free.
-
(ii) If
 $t$
is even and
$t$
is even and
 $\prod _{i\in [t]}a_i$
is a non-square, then the induced subgraph of
$\prod _{i\in [t]}a_i$
is a non-square, then the induced subgraph of
 $\mathrm{AK}_{B}(t-1,q)$
on
$\mathrm{AK}_{B}(t-1,q)$
on
 $X_{B,\boxtimes }/{\sim }$
is a
$X_{B,\boxtimes }/{\sim }$
is a
 $K_{t}$
-free.
$K_{t}$
-free.
-
(iii) If
 $\prod _{i\in [t]}a_i$
is a non-square, then the induced subgraph of
$\prod _{i\in [t]}a_i$
is a non-square, then the induced subgraph of
 $\mathrm{AK}_{B}(t-1,q)$
on
$\mathrm{AK}_{B}(t-1,q)$
on
 $X_{B,\Box }/{\sim }$
is a
$X_{B,\Box }/{\sim }$
is a
 $K_{t}$
-free.
$K_{t}$
-free.
Proof. Suppose that there exists a set
![]() $S = \left \{[\![\textbf{x}_1]\!],\ldots, [\![\textbf{x}_t]\!] \right \} \subset (X_{B,\boxtimes }\cup X_{B,\Box })/{\sim }$
is a set of
$S = \left \{[\![\textbf{x}_1]\!],\ldots, [\![\textbf{x}_t]\!] \right \} \subset (X_{B,\boxtimes }\cup X_{B,\Box })/{\sim }$
is a set of
![]() $t$
distinct points such that the induced subgraph of
$t$
distinct points such that the induced subgraph of
![]() $\mathrm{AK}_{B}(t-1,q)$
on
$\mathrm{AK}_{B}(t-1,q)$
on
![]() $S$
is complete. Then it follows from Fact 4.1 that there exists a non-zero element
$S$
is complete. Then it follows from Fact 4.1 that there exists a non-zero element
![]() $a\in \mathbb{F}_{q}$
such that
$a\in \mathbb{F}_{q}$
such that
![]() $\textbf{x}_{t} = a \textbf{x}_{1}\times \cdots \times \textbf{x}_{t-1}$
. Therefore, by Theorem 4.2, we have
$\textbf{x}_{t} = a \textbf{x}_{1}\times \cdots \times \textbf{x}_{t-1}$
. Therefore, by Theorem 4.2, we have
 \begin{align*} B(\textbf{x}_{t}, \textbf{x}_{t}) & = B(a \textbf{x}_{1}\times \cdots \times \textbf{x}_{t-1},\ a\textbf{x}_{1}\times \cdots \times \textbf{x}_{t-1}) \\ & =a^2 \cdot \prod _{i\in [t]}a_i \cdot \mathrm{det} \begin{bmatrix} B(\textbf{x}_1, \textbf{x}_1) && \dots && B(\textbf{x}_1, \textbf{x}_{t-1}) \\ \vdots && \ddots && \vdots \\ B(\textbf{x}_{t-1}, \textbf{x}_1) && \dots && B(\textbf{x}_{t-1}, \textbf{x}_{t-1}) \end{bmatrix} = a^2 \cdot \prod _{i\in [t]}a_i \cdot \prod _{i=1}^{t-1} B\left (\textbf{x}_i, \textbf{x}_i\right ). \end{align*}
\begin{align*} B(\textbf{x}_{t}, \textbf{x}_{t}) & = B(a \textbf{x}_{1}\times \cdots \times \textbf{x}_{t-1},\ a\textbf{x}_{1}\times \cdots \times \textbf{x}_{t-1}) \\ & =a^2 \cdot \prod _{i\in [t]}a_i \cdot \mathrm{det} \begin{bmatrix} B(\textbf{x}_1, \textbf{x}_1) && \dots && B(\textbf{x}_1, \textbf{x}_{t-1}) \\ \vdots && \ddots && \vdots \\ B(\textbf{x}_{t-1}, \textbf{x}_1) && \dots && B(\textbf{x}_{t-1}, \textbf{x}_{t-1}) \end{bmatrix} = a^2 \cdot \prod _{i\in [t]}a_i \cdot \prod _{i=1}^{t-1} B\left (\textbf{x}_i, \textbf{x}_i\right ). \end{align*}
In the last equality, we used the fact that
![]() $B(\textbf{x}_i, \textbf{x}_j) = 0$
for all
$B(\textbf{x}_i, \textbf{x}_j) = 0$
for all
![]() $i\neq j$
. Applying the quadratic character
$i\neq j$
. Applying the quadratic character
![]() $\chi (\cdot )$
to both sides of the equation above, we obtain
$\chi (\cdot )$
to both sides of the equation above, we obtain
 \begin{align*} \chi \left (B(\textbf{x}_{t}, \textbf{x}_{t}) \right ) & = \chi \left (a^2\cdot \prod _{i\in [t]}a_i \cdot \prod _{i=1}^{t-1} B\left (\textbf{x}_i, \textbf{x}_i\right )\right ) \\ & = \chi (a^2) \cdot \chi \left (\prod _{i\in [t]}a_i\right ) \cdot \prod _{i=1}^{t-1} \chi \left (B(\textbf{x}_i, \textbf{x}_i)\right ) = \chi \left (\prod _{i\in [t]}a_i\right ) \cdot \prod _{i=1}^{t-1} \chi \left (B(\textbf{x}_i, \textbf{x}_i)\right ), \end{align*}
\begin{align*} \chi \left (B(\textbf{x}_{t}, \textbf{x}_{t}) \right ) & = \chi \left (a^2\cdot \prod _{i\in [t]}a_i \cdot \prod _{i=1}^{t-1} B\left (\textbf{x}_i, \textbf{x}_i\right )\right ) \\ & = \chi (a^2) \cdot \chi \left (\prod _{i\in [t]}a_i\right ) \cdot \prod _{i=1}^{t-1} \chi \left (B(\textbf{x}_i, \textbf{x}_i)\right ) = \chi \left (\prod _{i\in [t]}a_i\right ) \cdot \prod _{i=1}^{t-1} \chi \left (B(\textbf{x}_i, \textbf{x}_i)\right ), \end{align*}
which is impossible in the following three cases:
![]() $t$
is odd,
$t$
is odd,
![]() $\prod _{i\in [t]}a_i$
is a square, and
$\prod _{i\in [t]}a_i$
is a square, and
![]() $S \subset X_{B,\boxtimes }/{\sim }$
;
$S \subset X_{B,\boxtimes }/{\sim }$
;
![]() $t$
is even,
$t$
is even,
![]() $\prod _{i\in [t]}a_i$
is a non-square, and
$\prod _{i\in [t]}a_i$
is a non-square, and
![]() $S \subset X_{B,\boxtimes }/{\sim }$
;
$S \subset X_{B,\boxtimes }/{\sim }$
;
![]() $\prod _{i\in [t]}a_i$
is a non-square, and
$\prod _{i\in [t]}a_i$
is a non-square, and
![]() $S \subset X_{B,\Box }/{\sim }$
.
$S \subset X_{B,\Box }/{\sim }$
.
Acknowledgement
We would like to thank Anurag Bishnoi, Ferdinand Ihringer, Jie Han, Thang Pham, and a referee for their insightful comments. Special thanks to a referee for informing us about reference [Reference Bannai, Shimabukuro and Tanaka7] and for providing valuable feedback that significantly enhanced Section 4. The first author would also like to thank Minghui Ma for very helpful discussions on the Hodge star map.