No CrossRef data available.
Article contents
Twin-width of sparse random graphs
Part of:
Graph theory
Published online by Cambridge University Press: 11 December 2024
Abstract
We show that the twin-width of every  $n$-vertex
$n$-vertex 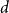 $d$-regular graph is at most
$d$-regular graph is at most 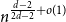 $n^{\frac{d-2}{2d-2}+o(1)}$ for any fixed integer
$n^{\frac{d-2}{2d-2}+o(1)}$ for any fixed integer 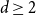 $d \geq 2$ and that almost all
$d \geq 2$ and that almost all 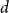 $d$-regular graphs attain this bound. More generally, we obtain bounds on the twin-width of sparse Erdős–Renyi and regular random graphs, complementing the bounds in the denser regime due to Ahn, Chakraborti, Hendrey, Kim, and Oum.
$d$-regular graphs attain this bound. More generally, we obtain bounds on the twin-width of sparse Erdős–Renyi and regular random graphs, complementing the bounds in the denser regime due to Ahn, Chakraborti, Hendrey, Kim, and Oum.
Keywords
MSC classification
Secondary:
05C80: Random graphs
Information
- Type
- Paper
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press
References
Ahn, J., Chakraborti, D., Hendrey, K., Kim, D. and Oum, S.-il. (2024) Twin-width of random graphs. Random Struct. Algor. 65 794–831. DOI: 10.1002/rsa.21247.CrossRefGoogle Scholar
Ahn, J., Chakraborti, D., Hendrey, K. and Oum, S.-il. (2023) Twin-width of subdivisions of multigraphs. URL: http://arxiv.org/abs/2306.05334
Google Scholar
Ahn, J., Hendrey, K., Kim, D. and Oum, S.-il. (2022) Bounds for the Twin-Width of Graphs. SIAM J. Discrete Math. 36 2352–2366. DOI: 10.1137/21M1452834.CrossRefGoogle Scholar
Anantharam, V. and Salez, J. (2016) The densest subgraph problem in sparse random graphs. Ann. Appl. Probab. 26 305–327. DOI: 10.1214/14-AAP1091
CrossRefGoogle Scholar
Bonnet, É., Geniet, C., Kim, E. J., Thomassé, S. and Watrigant, R. (2022) Twin-width II: small classes. Comb. Theory 2 DOI: 10.5070/C62257876
Google Scholar
Bonnet, É., Kim, E. J., Thomassé, S. and Watrigant, R. (2022) Twin-width I: Tractable FO Model Checking. J Acm. 69 1–46. DOI: 10.1145/3486655.CrossRefGoogle Scholar
Hajek, B. (1990) Performance of global load balancing by local adjustment. IEEE T. Inform. Theory 36 1398–1414. DOI: 10.1109/18.59935.CrossRefGoogle Scholar
Hajnal, A. and Szemerédi, E. (1970) Proof of a Conjecture of Erdős. In Combinatorial Theory and Its Applications, Vol. 2 (P. Erdős, A. Rényi, and V. T. Sós, eds). Amsterdam, Netherlands: North-Holland, pp. 601–623.Google Scholar
Lord, N. (2010) Binomial averages when the mean is an integer. Math. Gaz. 94 331–332. DOI: 10.1017/S0025557200006690.CrossRefGoogle Scholar
McDiarmid, C. (1998) Concentration. In Probabilistic methods for algorithmic discrete mathematics, Algorithms and Combinatorics, Vol. 16, Springer, pp. 195–248.
CrossRefGoogle Scholar
McKay, B. D. and Wormald, N. C. (1991) Asymptotic enumeration by degree sequence of graphs with degreeso(n 1/2). Combinatorica 11 369–382. DOI: 10.1007/BF01275671.CrossRefGoogle Scholar
Sylvester, J. Open Problems - 1st Twin-Width Workshop 2023, Problem 9. Private communicationGoogle Scholar


