Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Anthony, M.
1995.
Interpolation and Learning in Artificial Neural Networks.
Vol. 6,
Issue. ,
p.
2928.
Natarajan, B.
2000.
On Learning Functions from Noise-Free and Noisy Samples via Occam's Razor.
SIAM Journal on Computing,
Vol. 29,
Issue. 3,
p.
712.
Meer, Klaus
and
Ziegler, Martin
2024.
Unconventional Computation and Natural Computation.
Vol. 14776,
Issue. ,
p.
58.

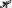 and
and 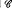 be sets of functions from domain
be sets of functions from domain  on
on