Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-10T11:20:12.110Z Has data issue: false hasContentIssue false
  • English
  • Français

Kinetic Energy Preserving and Entropy Stable Finite Volume Schemes for Compressible Euler and Navier-Stokes Equations

Published online by Cambridge University Press:  03 June 2015

Praveen Chandrashekar
Praveen Chandrashekar*
Affiliation:
TIFR Center for Applicable Mathematics, Bangalore 560065, India
*
*Corresponding author.Email:praveen@math.tifrbng.res.in
Get access

Abstract

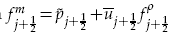Centered numerical fluxes can be constructed for compressible Euler equations which preserve kinetic energy in the semi-discrete finite volume scheme. The essential feature is that the momentum flux should be of the form where 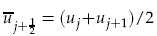and 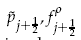are any consistent approximations to the pressure and the mass flux. This scheme thus leaves most terms in the numerical flux unspecified and various authors have used simple averaging. Here we enforce approximate or exact entropy consistency which leads to a unique choice of all the terms in the numerical fluxes. As a consequence novel entropy conservative flux that also preserves kinetic energy for the semi-discrete finite volume scheme has been proposed. These fluxes are centered and some dissipation has to be added if shocks are present or if the mesh is coarse. We construct scalar artificial dissipation terms which are kinetic energy stable and satisfy approximate/exact entropy condition. Secondly, we use entropy-variable based matrix dissipation flux which leads to kinetic energy and entropy stable schemes. These schemes are shown to be free of entropy violating solutions unlike the original Roe scheme. For hypersonic flows a blended scheme is proposed which gives carbuncle free solutions for blunt body flows. Numerical results for Euler and Navier-Stokes equations are presented to demonstrate the performance of the different schemes.

Keywords

65M0865M12Euler equationNavier-Stokes equationfinite volume methodkinetic energy preservationentropy conservation
Type
Research Article
Information
Communications in Computational Physics , Volume 14 , Issue 5 , November 2013 , pp. 1252 - 1286
Copyright
Copyright © Global Science Press Limited 2013

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Barth, T. and Ohlberger, M.Finite volume methods: Foundation and analysis. In Stein, E., Borst, R. D., and Hughes, T. J., editors, Encyclopedia of Computational Mechanics, volume 1, chapter 15. Wiley, 2004.Google Scholar
[2]Blaisdell, G., Spyropoulos, E., and Qin, J.The effect of the formulation of nonlinear terms on aliasing errors in spectral methods. Applied Numerical Mathematics, 21(3):207–219, 1996.Google Scholar
[3]Dumbser, M. and Toro, E. F.On universal Osher-type schemes for general nonlinear hyperbolic conservation laws. Commun. Comput. Phys., 10:635–671, 2011.CrossRefGoogle Scholar
[4]Fjordholm, U., Mishra, S., and Tadmor, E.Arbitrarily high-order accurate entropy stable essentially nonoscillatory schemes for systems of conservation laws. SIAM Journal on Numerical Analysis, 50(2):544–573, 2012.CrossRefGoogle Scholar
[5]Gerritsen, M. and Olsson, P.Designing an efficient solution strategy for fluid flows: 1. A stable high orderfinite differencescheme and sharp shock resolution for the Euler equations. Journal of Computational Physics, 129(2):245–262, 1996.Google Scholar
[6]Geuzaine, C. and Remacle, J.-F.Gmsh: A 3-d finite element mesh generator with built-in preand post-processing facilities. International Journal for Numerical Methods in Engineering, 79(11):1309–1331, 2009.Google Scholar
[7]Harten, A.On the symmetric form of systems of conservation laws with entropy. Journal of Computational Physics, 49(1):151–164, 1983.Google Scholar
[8]Honein, A. E. and Moin, P.Higher entropy conservation and numerical stability of compressible turbulence simulations. Journal of Computational Physics, 201(2):531–545, 2004.Google Scholar
[9]Hughes, T., Franca, L., and Mallet, M.A new finite element formulation for computational fluid dynamics: I. Symmetric forms of the compressible Euler and Navier-Stokes equations and the second law of thermodynamics. Computer Methods in Applied Mechanics and Engineering, 54(2):223–234, 1986.CrossRefGoogle Scholar
[10]Ismail, F. and Roe, P. L.Affordable, entropy-consistent Euler flux functions II: Entropy production at shocks. J. Comput. Phys., 228(15):5410–5436, Aug. 2009.Google Scholar
[11]Ismail, F., Roe, P. L., and Nishikawa, H.A proposed cure to the carbuncle phenomenon. In Computational Fluid Dynamics (2006): Proc. of Fourth International Conference on CFD, Ghent, Belgium, July 2006.Google Scholar
[12]Jameson, A.Formulation of kinetic energy preserving conservative schemes for gas dynamics and direct numerical simulation of one-dimensional viscous compressible flow in a shock tube using entropy and kinetic energy preserving schemes. J. Sci. Comput., 34(2):188–208, Feb. 2008.Google Scholar
[13]Jameson, A., Schmidt, W., and Turkel, E.Numerical solution of the Euler equations by finite volume methods using Runge-Kutta time-stepping schemes. In AIAA 14th Fluid and Plasma Dynamic Conference, Palo Alto, California, June 1981.Google Scholar
[14]Kennedy, C. A. and Gruber, A.Reduced aliasing formulations of the convective terms within the Navier-Stokes equations for a compressible fluid. Journal of Computational Physics, 227(3):1676–1700, 2008.Google Scholar
[15]Le, P.Floch, Mercier, J., and Rohde, C.Fully discrete, entropy conservative schemes of arbitraryorder. SIAM Journal on Numerical Analysis, 40(5):1968–1992, 2002.Google Scholar
[16]Morinishi, Y.Skew-symmetric form of convective terms and fully conservative finite difference schemes for variable density low-mach number flows. Journal of Computational Physics, 229(2):276–300, 2010.Google Scholar
[17]Muller, J.-D.On Triangles and flow. PhD thesis, The University of Michigan, 1996.Google Scholar
[18]Pirozzoli, S.Numerical methods for high-speed flows. Annual Review of Fluid Mechanics, 43(1):163–194, 2011.Google Scholar
[19]Quirk, J. J.A contribution to the great Riemann solver debate. International Journal for Numerical Methods in Fluids, 18(6):555–574, 1994.Google Scholar
[20]Roe, P. L.Approximate Riemann solvers, parameter vectors, and differenceschemes. Journal of Computational Physics, 43(2):357–372, 1981.Google Scholar
[21]Roe, P. L.Affordable, entropy consistent flux functions. In Eleventh International Conference on Hyperbolic Problems: Theory, Numerics and Applications, Lyon, 2006.Google Scholar
[22]Scandaliato, A. L. and Liou, M.-S.AUSM-based high-order solution for Euler equations. Commun. Comput. Phys., 12:1096–1120, 2012.Google Scholar
[23]Shoeybi, M., Svard, M., Ham, F. E., and Moin, P.An adaptive implicit-explicit scheme for the DNS and LES of compressible flows on unstructured grids. Journal of Computational Physics, 229(17):5944–5965, 2010.Google Scholar
[24]Shu, C.-W. and Osher, S.Efficient implementation of essentially non-oscillatory shock-capturing schemes. Journal of Computational Physics, 77(2):439–471, 1988.CrossRefGoogle Scholar
[25]Subbareddy, P. K. and Candler, G. V.A fully discrete, kinetic energy consistent finite-volume scheme for compressible flows. Journal of Computational Physics, 228(5):1347–1364, 2009.Google Scholar
[26]Tadmor, E.The numerical viscosity of entropy stable schemes for systems of conservation laws. I. Mathematics of Computation, 49(179):91–103,1987.Google Scholar
[27]Tadmor, E.Entropy stability theory for difference approximations of nonlinear conservation laws and related time-dependent problems. Acta Numerica, pp. 451–512, 2004.Google Scholar
[28] B.Thornber, Drikakis, D., Williams, R., and Youngs, D.On entropy generation and dissipation of kinetic energy in high-resolution shock-capturing schemes. Journal of Computational Physics, 227(10):4853–4872, 2008.Google Scholar
[29]Leer, B. van. Upwind and high-resolution methods for compressible flow: From donor cell to residual-distribution schemes. Commun. Comput. Phys., 1:192–206, 2006.Google Scholar
[30]Woodward, P. and Colella, P.The numerical simulation of two-dimensional fluid flow with strong shocks. Journal of Computational Physics, 54(1):115–173, 1984.Google Scholar
[31]Wu, H., Shen, L., and Shen, Z.A hybrid numerical method to cure numerical shock instability. Commun. Comput. Phys., 8:1264–1271, 2010.CrossRefGoogle Scholar