Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-10T15:44:58.495Z Has data issue: false hasContentIssue false
  • English
  • Français

A Novel Numerical Method of 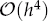for Three-Dimensional Non-Linear Triharmonic Equations

Published online by Cambridge University Press:  20 August 2015

R. K. Mohanty ,
M. K. Jain  and
B. N. Mishra
R. K. Mohanty*
Affiliation:
Department of Mathematics, Faculty of Mathematical Sciences, University of Delhi, Delhi-110 007, India
M. K. Jain
Affiliation:
Department of Mathematics, Indian Institute of Technology, Hauz Khas, New Delhi-110 016, India
B. N. Mishra*
Affiliation:
Department of Mathematics, Utkal University, Vani Vihar, Bhubaneswar-751 004, India
*
Corresponding author.Email address:rmohanty@maths.du.ac.in
Email address:bn_misramath@hotmail.com
Get access

Abstract

In this article, we present two new novel finite difference approximations of order two and four, respectively, for the three dimensional non-linear triharmonic partial differential equations on a compact stencil where the values of u, ∂2u/∂n2 and ∂4u/∂n4 are prescribed on the boundary. We introduce new ideas to handle the boundary conditions and there is no need to discretize the derivative boundary conditions. We require only 7- and 19-grid points on the compact cell for the second and fourth order approximation, respectively. The Laplacian and the biharmonic of the solution are obtained as by-product of the methods. We require only system of three equations to obtain the solution. Numerical results are provided to illustrate the usefulness of the proposed methods.

Keywords

65N0602.60.Lj02.70.BfFinite differencesthree dimensional non-linear triharmonic equationsfourth order compact discretizationLaplacianbiharmonicmaximum absolute errors
Type
Research Article
Information
Communications in Computational Physics , Volume 12 , Issue 5 , November 2012 , pp. 1417 - 1433
Copyright
Copyright © Global Science Press Limited 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Smith, J., The coupled equation approach to the numerical solution of the biharmonic equation by finite differences, SIAM. J. Numer. Anal., 5 (1970), 104–111.Google Scholar
[2]Ehrlich, L. W., Solving the Biharmonic equation as coupled finite difference equations, SIAM. J. Numer. Anal., 8 (1971), 278–287.Google Scholar
[3]Ehrlich, L. W., Point and block SOR applied to a coupled set of difference equations, Computing, 12 (1974), 181–194.Google Scholar
[4]Bauer, L. and Riess, E. L., Block five diagonal matrices and the fast numerical solution of the biharmonic equation, Math. Comput., 26 (1972), 311–326.Google Scholar
[5]Kwon, Y., Manohar, R. and Stephenson, J. W., Single cell fourth order methods for the biharmonic equation, Congress Numerantium, 34 (1982), 475–482.Google Scholar
[6]Stephenson, J. W., Single cell discretization of order two and four for biharmonic problems, J. Comput. Phys., 55 (1984), 65–80.CrossRefGoogle Scholar
[7]Evans, D. J. and Mohanty, R. K., Block iterative methods for the numerical solution of two-dimensional non-linear biharmonic equations, Int. J. Comput. Math., 69 (1998), 371–390.CrossRefGoogle Scholar
[8]Mohanty, R. K., Jain, M. K. and Pandey, P. K., Finite difference methods of order two and four for 2D non-linear biharmonic problems of first kind, Int. J. Comput. Math., 61 (1996), 155163.Google Scholar
[9]Mohanty, R. K. and Pandey, P. K., Difference methods of order two and four for systems of mildly non-linear biharmonic problems of second kind in two space dimensions, Numer. Meth.Partial Diff. Eq., 12 (1996), 707–717.3.0.CO;2-W>CrossRefGoogle Scholar
[10]Mohanty, R. K. and Pandey, P. K., Families of accurate discretization of order two and four for 3D mildlyy non-linear biharmonic problems of second kind, Int. J. Comput. Math., 68 (1998), 363–380.CrossRefGoogle Scholar
[11]Mohanty, R. K., Evans, D. J. and Pandey, P. K., Block iterative methods for the numerical solution of three-dimensional non-linear biharmonic equations of first kind, Int. J. Comput. Math., 77 (2001), 319–332.Google Scholar
[12]Jain, M. K., Jain, R. K. and Mohanty, R. K., Fourth order finite difference method for three dimensional elliptic equations with non-linear first derivative terms, Numer. Meth. Partial Diff. Eq., 8 (1992), 575–559.Google Scholar
[13]Mohanty, R. K. and Singh, S., A new highly accurate discretization for three dimensional singularly perturbed non-linear elliptic partial differential equations, Numer. Meth. Partial Diff. Eq., 22 (2006), 1379–1395.Google Scholar
[14]Spotz, W. F. and Carey, G. F., High-order compact scheme for the steady stream-function vorticity equations, Int. J. Numer. Meth. Eng., 38 (1995), 3497–3512.CrossRefGoogle Scholar
[15]Li, M., Tang, T. and Fornberg, B., A compact fourth order finite difference scheme for the steady incompressible Navier-Stokes equations, Int. J. Numer. Meth. Fluids, 20 (1995), 11371151.CrossRefGoogle Scholar
[16]Tian, Z. F. and Ge, Y. B., A fourth-order compact finite difference scheme for the steady stream function-vorticity formulation of the Navier-Stokes/Boussinesq equations, Int. J. Numer. Meth. Fluids, 41 (2003), 495–518.Google Scholar
[17]Tian, Z. F. and Ge, Y. B., A fourth order compact ADI method for solving two-dimensional unsteady convection-diffusion problems, J. Comput. Appl. Math., 198 (2007), 268–286.Google Scholar
[18]Tian, Z. F. and Dai, S. Q., High order compact exponential finite difference methods for convection-diffusion type problems, J. Comput. Phys., 220 (2007), 952–974.Google Scholar
[19]Erturk, E. and Gokcol, C., Fourth order compact formulation of Navier-Stokes equations and driven cavity flow at high Reynolds number, Int. J. Numer. Meth. Fluids, 50 (2006), 421–436.Google Scholar
[20]Singh, Swarn, Khattar, Dinesh and Mohanty, R. K., A new coupled approach high accuracy numerical method for the solution of 2D non-linear biharmonic equations, Neural Parallel and Scientific Computations, 17 (2009), 239–256.Google Scholar
[21]Khattar, Dinesh, Singh, Swarn and Mohanty, R. K., A new coupled approach high accuracy method for the solution of 3D non-linear biharmonic equations, Appl. Math. Comput., 215 (2009), 3036–3044.Google Scholar
[22]Mohanty, R. K., Single-cell compact finite-difference discretization of order two and four for multidimensional triharmonic problems, Numer. Meth. Partial Diff. Eq., 26 (2010), 14201426.Google Scholar
[23]Mohanty, R. K., A new high accuracy finite difference discretizationr for the solution of 2D non-linear biharmonic equations using coupled approach, Numer. Meth. Partial Diff. Eq., 26 (2010), 931–944.CrossRefGoogle Scholar
[24]Mohanty, R. K., Jain, M. K. and Mishra, B. N., A compact discretization of O(h4) for twodimensional nonlinear triharmonic equations, Phys. Scr., 84 (2011), 025002.Google Scholar
[25]Parter, S. V., Block Iterative Methods in Elliptic Problem Solvers, Schultz, M. H. Ed., Academic Press, 1981.Google Scholar
[26]Kelly, C. T., Iterative Methods for Linear and Non-Linear Equations, SIAM publications, Philadelphia, 1995.Google Scholar
[27]Meurant, G., Computer Solution of Large Linear Systems, North-Holland, 1999.Google Scholar
[28]Varga, R. S., Matrix Iterative Analysis, Springer Verlag, 2000.Google Scholar
[29]Saad, Y., Iterative Methods for Sparse Linear Systems, SIAM publications, Philadelphia, 2003.Google Scholar
[30]Hageman, L. A. and Young, D. M., Applied Iterative Methods, Dover Publication, New York, 2004.Google Scholar