Hostname: page-component-78c5997874-8bhkd Total loading time: 0 Render date: 2024-11-10T16:28:18.910Z Has data issue: false hasContentIssue false
  • English
  • Français

An Essential Extension of the Finite-Energy Condition for Extended Runge-Kutta-Nyström Integrators when Applied to Nonlinear Wave Equations

Part of: Partial differential equations, initial value and time-dependent initial-boundary value problems Numerical analysis: Ordinary differential equations

Published online by Cambridge University Press:  06 July 2017

Lijie Mei ,
Changying Liu  and
Xinyuan Wu
Lijie Mei*
Affiliation:
School of Mathematics & Computer Science, Shangrao Normal University, Shangrao 334001, P.R. China
Changying Liu*
Affiliation:
Department of Mathematics, Nanjing University; State Key Laboratory for Novel Software Technology at Nanjing University, Nanjing 210093, P.R. China
Xinyuan Wu*
Affiliation:
School of Mathematical Sciences, Qufu Normal University, Qufu 273165, P.R. China
*
*Corresponding author. Email addresses:bxhanm@126.com (L. Mei), chyliu88@gmail.com (C. Liu), xywu@nju.edu.cn (X.Wu)
*Corresponding author. Email addresses:bxhanm@126.com (L. Mei), chyliu88@gmail.com (C. Liu), xywu@nju.edu.cn (X.Wu)
*Corresponding author. Email addresses:bxhanm@126.com (L. Mei), chyliu88@gmail.com (C. Liu), xywu@nju.edu.cn (X.Wu)
Get access

Abstract

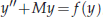This paper is devoted to an extension of the finite-energy condition for extended Runge-Kutta-Nyström (ERKN) integrators and applications to nonlinear wave equations. We begin with an error analysis for the integrators for multi-frequency highly oscillatory systems , where M is positive semi-definite, 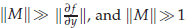. The highly oscillatory system is due to the semi-discretisation of conservative, or dissipative, nonlinear wave equations. The structure of such a matrix M and initial conditions are based on particular spatial discretisations. Similarly to the error analysis for Gaustchi-type methods of order two, where a finite-energy condition bounding amplitudes of high oscillations is satisfied by the solution, a finite-energy condition for the semi-discretisation of nonlinear wave equations is introduced and analysed. These ensure that the error bound of ERKN methods is independent of 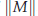. Since stepsizes are not restricted by frequencies of M, large stepsizes can be employed by our ERKN integrators of arbitrary high order. Numerical experiments provided in this paper have demonstrated that our results are truly promising, and consistent with our analysis and prediction.

Keywords

Finite-energy conditionmulti-frequency highly oscillatory systemerror analysisERKN methodnonlinear wave equation

MSC classification

Secondary: 65L70: Error bounds 65L05: Initial value problems 65L06: Multistep, Runge-Kutta and extrapolation methods 65M20: Method of lines
Type
Research Article
Information
Communications in Computational Physics , Volume 22 , Issue 3 , September 2017 , pp. 742 - 764
Copyright
Copyright © Global-Science Press 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1] Bratsos, A. G., On the Numerical Solution of the Klein-Gordon Equation, Numer. Methods Partial Differ. Equ. 25 (2009) 939–951.CrossRefGoogle Scholar
[2] Brugnano, L., G. Frasca Caccia, Iavernaro, F., Energy conservation issues in the numerical solution of the semilinear wave equation, Appl. Math. Comput. (270) (2015) 842–870.Google Scholar
[3] Cohen, D., Hairer, E., Lubich, C., Numerical energy conservation for multi-frequency oscillatory differential equations, BIT 45 (2005) 287–305.CrossRefGoogle Scholar
[4] Franco, J. M., Runge-Kutta-Nyström methods adapted to the numerical integration of perturbed oscillators, Comput. Phys. Comm. 147 (2002) 770–787.CrossRefGoogle Scholar
[5] Franco, J.M., Exponentially fitted explicit Runge-Kutta-Nyström methods, J. Comput. Appl. Math. 167 (2004) 1–19.CrossRefGoogle Scholar
[6] Franco, J. M., New methods for oscillatory systems based on ARKN methods, Appl. Numer. Math. 56 (2006) 1040–1053.CrossRefGoogle Scholar
[7] GarcÍa-Archillay, B., Sanz-Serna, J. M., Skeel, R. D., Long-time-step methods for oscillatory differential equations, SIAM J. Sci. Comput. 20 (1998) 930–963.CrossRefGoogle Scholar
[8] Grimm, V., On error bounds for the Gautschi-type exponential integrator applied to oscillatory second-order differential equations, Numer. Math. 100 (2005) 71–89.CrossRefGoogle Scholar
[9] Grimm, V., On the use of the Gautschi-type exponential integrator for wave equations, The 6th European Conference on Numerical Mathematics and Advanced Applications, Santiago de Compostela, Spain, 2005.Google Scholar
[10] Grimm, V., Hochbruck, M., Error analysis of exponential integrators for oscillatory second-order differential equations, J. Phys. A: Math. Gen. 39 (2006) 5495–5507.CrossRefGoogle Scholar
[11] Hairer, E., Lubich, C.. Long-time energy conservation of numerical methods for oscillatory differential equations, SIAM J. Numer. Anal. 38 (2000) 414–441.CrossRefGoogle Scholar
[12] Hairer, E., Lubich, C., Wanner, G., Geometric Numerical Integration: Structure-Preserving Algorithms for Ordinary Differential Equations, 2nd ed., Springer-Verlag, Berlin, Heidelberg, 2006.Google Scholar
[13] Hochbruck, M., Lubich, C., A Gautschi-type method for oscillatory second-order differential equations, Numer. Math. 83 (1999) 403–426.CrossRefGoogle Scholar
[14] Hochbruck, M., Ostermann, A., Explicit exponential Runge-Kutta methods for semilinear parabolic problems, SIAM J. Numer. Anal. 43 (2005) 1069–1090.CrossRefGoogle Scholar
[15] Hochbruck, M., Ostermann, A., Exponential integrators, Acta Numer. 19 (2010) 209–286.CrossRefGoogle Scholar
[16] Kress, R., Numerical Analysis, Springer-Verlag, Berlin, 1998.CrossRefGoogle Scholar
[17] Li, J., Wu, X., Error analysis of explicit TSERKN methods for highly oscillatory systems, Numer. Algor. 65 (2014) 465–483.CrossRefGoogle Scholar
[18] Li, Y.W., Wu, X., Exponential integrators preserving first integrals or Lyapunov functions for conservative or dissipative systems, SIAM J. Sci. Comput. 38 (2016) A1876–A1895.CrossRefGoogle Scholar
[19] Li, Y.W., Wu, X., Functionally-fitted energy-preserving methods for solving oscillatory nonlinear Hamiltonian systems, SIAM J. Numer. Anal. 54 (2016) 2036–2059.CrossRefGoogle Scholar
[20] Liu, K., Shi, W., Wu, X., An extended discrete gradient formula for oscillatory Hamiltonian systems, J. Phys. A: Math. Theor. 46 (2013) 165203 (1-19).CrossRefGoogle Scholar
[21] Liu, C., Shi, W., Wu, X., An efficient high-order explicit scheme for solving Hamiltonian nonlinear wave equations, Appl. Math. Compu. 246 (2014) 696–710.Google Scholar
[22] Liu, K., Wu, X., Multidimensional ARKN methods for general oscillatory second-order initial value problems, Comput. Phys. Comm. 185 (2014) 1999–2007.CrossRefGoogle Scholar
[23] Liu, K., Wu, X., High-order symplectic and symmetric composition methods for multi-frequency and multi-dimensional oscillatory Hamiltonian systems, J. Comput. Math. 33 (2015) 356–378.Google Scholar
[24] Schiesser, W. E., Griffiths, G. W., A Compendium of Partial Differential Equation Models: Method of Lines Analysis with Matlab, Cambridge University Press, Cambridge, New York, 2009.CrossRefGoogle Scholar
[25] Shi, W., Wu, X., Xia, J., Explicit multi-symplectic extended leap-frog methods for Hamiltonian wave equations, J. Comput. Phys., 231 (2012) 7671–7694.CrossRefGoogle Scholar
[26] Trefethen, L.N., Spectral Methods in MATLAB, SIAM, Philadelphia, 2000.CrossRefGoogle Scholar
[27] Vanden Berghe, G., De Meyer, H., Van Daele, M., Van Hecke, T., Exponentially fitted Runge-Kutta methods, J. Comput. Appl. Math. 125 (2000) 107–115.CrossRefGoogle Scholar
[28] Verwer, J. G., Sanz-Serna, J. M., Convergence of method of lines approximations to partial differential equations, Computing 33 (1984) 297–313.CrossRefGoogle Scholar
[29] Wang, B., Iserles, A., Wu, X., Arbitrary-order trigonometric Fourier collocation methods for multi-frequency oscillatory systems, Found. Comput. Math. 16 (2016) 151–181.CrossRefGoogle Scholar
[30] Wang, B., Wu, X., Explicit multi-frequency symmetric extended RKN integrators for solving multi-frequency and multidimensional oscillatory reversible systems, Calcolo, 52 (2015) 207–231.CrossRefGoogle Scholar
[31] Wang, B., Wu, X., Xia, J., Error bounds for explicit ERKN integrators for systems of multi-frequency oscillatory second-order differential equations, Appl. Numer. Math. 74 (2013) 17–34.CrossRefGoogle Scholar
[32] Wu, X., Liu, K., Shi, W., Structure-Preserving Algorithms for Oscillatory Differential Equations II, Springer-Verlag, Berlin, Heidelberg, 2015.CrossRefGoogle Scholar
[33] Wu, X., Liu, C., An integral formula adapted to different boundary conditions for arbitrarily high-dimensional nonlinear Klein-Gordon equations with its applications, J. Math. Phys. 57 (2016), 021504.CrossRefGoogle Scholar
[34] Wu, X., Mei, L., Liu, C., An analytical expression of solutions to nonlinear wave equations in higher dimensions with Robin boundary conditions, J. Math. Anal. Appl. 426 (2015) 1164–1173.CrossRefGoogle Scholar
[35] Wu, X., Wang, B., Liu, K., Zhao, H., ERKN methods for long-term integration of multidimensional orbital problems, Appl. Math. Modell. 37 (2013) 2327–2336.CrossRefGoogle Scholar
[36] Wu, X., Wang, B., Shi, W., Efficient energy-preserving integrators for oscillatory Hamiltonian systems, J. Comput. Phys. 235 (2013) 587–605.CrossRefGoogle Scholar
[37] Wu, X., Wang, B., Xia, J., Explicit symplectic multidimensional exponential fitting modified Runge-Kutta-Nyström methods, BIT 52 (2012) 773–795.CrossRefGoogle Scholar
[38] Wu, X., You, X., Wang, B., Structure-Preserving Algorithms for Oscillatory Differential Equations, Springer-Verlag, Berlin, Heidelberg, 2013.CrossRefGoogle Scholar
[39] Wu, X., You, X., Shi, W., Wang, B., ERKN integrators for systems of oscillatory second-order differential equations, Comput. Phys. Comm. 181 (2010) 1873–1887.CrossRefGoogle Scholar
[40] Wu, X., You, X., Xia, J., Order conditions for ARKN methods solving oscillatory systems, Comput. Phys. Comm. 180 (2009) 2250–2257.CrossRefGoogle Scholar
[41] Yan, J., Zhang, Z., New energy-preserving schemes using Hamiltonian Boundary Value and Fourier pseudospectral methods for the numerical solution of the “good” Boussinesq equation, Comput. Phys. Comm. 201 (2016) 33–42.CrossRefGoogle Scholar
[42] Yang, H., Wu, X., You, X., Fang, Y., Extended RKN-type methods for numerical integration of perturbed oscillators, Comput. Phys. Comm. 180 (2009) 1777–1794.CrossRefGoogle Scholar
[43] Yang, H., Zeng, X., Wu, X., Ru, Z., A simplified Nyström-tree theory for extended Runge-Kutta-Nyström integrators solving multi-frequency oscillatory systems, Comput. Phys. Comm. 185 (2014) 2841–2850.CrossRefGoogle Scholar