Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-10T11:13:06.712Z Has data issue: false hasContentIssue false
  • English
  • Français

A Frequency Determination Method for Digitized NMR Signals

Published online by Cambridge University Press:  03 June 2015

H. Yan ,
K. Li ,
R. Khatiwada ,
E. Smith ,
W. M. Snow ,
C. B. Fu ,
P.-H. Chu ,
H. Gao  and
W. Zheng
H. Yan*
Affiliation:
Indiana University, Bloomington, Indiana 47408, USA Center for Exploration of Energy and Matter, Indiana University, Bloomington, IN 47408, USA
K. Li
Affiliation:
Indiana University, Bloomington, Indiana 47408, USA Center for Exploration of Energy and Matter, Indiana University, Bloomington, IN 47408, USA
R. Khatiwada
Affiliation:
Indiana University, Bloomington, Indiana 47408, USA Center for Exploration of Energy and Matter, Indiana University, Bloomington, IN 47408, USA
E. Smith
Affiliation:
Indiana University, Bloomington, Indiana 47408, USA Center for Exploration of Energy and Matter, Indiana University, Bloomington, IN 47408, USA
W. M. Snow
Affiliation:
Indiana University, Bloomington, Indiana 47408, USA Center for Exploration of Energy and Matter, Indiana University, Bloomington, IN 47408, USA
C. B. Fu
Affiliation:
Indiana University, Bloomington, Indiana 47408, USA Center for Exploration of Energy and Matter, Indiana University, Bloomington, IN 47408, USA Department of Physics, Shanghai Jiaotong University, Shanghai, 200240, China
P.-H. Chu
Affiliation:
Triangle Universities Nuclear Laboratory and Department of Physics, Duke University, Durham, North Carolina 27708, USA
H. Gao
Affiliation:
Triangle Universities Nuclear Laboratory and Department of Physics, Duke University, Durham, North Carolina 27708, USA
W. Zheng
Affiliation:
Triangle Universities Nuclear Laboratory and Department of Physics, Duke University, Durham, North Carolina 27708, USA
*
*Corresponding author.Email:haiyan@umail.iu.edu
Get access

Abstract

We present a high precision frequency determination method for digitized NMR FID signals. The method employs high precision numerical integration rather than simple summation as in many other techniques. With no independent knowledge of the other parameters of a NMR FID signal (phase ф, amplitude A, and transverse relaxation time T2) this method can determine the signal frequency f0 with a precision of 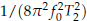if the observation time T ≫ T2. The method is especially convenient when the detailed shape of the observed FT NMR spectrum is not well defined. When T2 is +∞ and the signal becomes pure sinusoidal, the precision of the method is 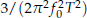which is one order more precise than the ±1 count error induced precision of a typical frequency counter. Analysis of this method shows that the integration reduces the noise by bandwidth narrowing as in a lock-in amplifier, and no extra signal filters are needed. For a pure sinusoidal signal we find from numerical simulations that the noise-induced error in this method reaches the Cramer-Rao Lower Band (CRLB) on frequency determination. For the damped sinusoidal case of most interest, the noise-induced error is found to be within a factor of 2 of CRLB when the measurement time T is 2 or 3 times larger than T2. We discuss possible improvements for the precision of this method.

Keywords

95.75.Wx02.70.-c43.50.+yNMRFIDnumerical integrationfrequency determinationnoise reduction
Type
Research Article
Information
Communications in Computational Physics , Volume 15 , Issue 5 , May 2014 , pp. 1343 - 1351
Copyright
Copyright © Global Science Press Limited 2014

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Zheng, W., Gao, H., Lalremruata, B., Zhang, Y., Laskaris, G., Fu, C.B., and Snow, W.M., Phys. Rev. D, 85, 031505(R) (2012).Google Scholar
[2]Bulatowicz, M., Larsen, M., Mirijanian, J., Walker, T.G., Fu, C.B., Smith, E., Snow, W.M., and Yan, H., to be published.Google Scholar
[3]Chu, P.-H., Fu, C.H., Gao, H., Khatiwada, R., Laskaris, G., Li, K., Smith, E., Snow, W.M., Yan, H., and Zheng, W., Phys. Rev. D, 87, 011105(R) (2013).Google Scholar
[4]Yang, J.-Z. and Liu, C.-W., IEEE Transactions on Power Delivery, 16, 361 (2001).Google Scholar
[5]Terzija, V.V., IEEE Transactions on Instrumentation and Measurement, 52, 1654 (2000).Google Scholar
[6]Obukhov, Y., Fong, K.C., Daughton, D., and Hammel, P.C., Journal of Applied Physics, 101, 034315 (2007).Google Scholar
[7]Press, W.H., Flannery, B.P., Teukolsky, S.A., and Vetterling, W.T., Numerical Recipes, Cambridge University Press (1989).Google Scholar
[8]Libbrecht, K.G., Black, E.D., and Hirta, C.M., Phys, Am. J., 71, 1208 (2003).Google Scholar
[9]Gemmel, C.et al., The European Physical Journal D, 57, 303 (2010).CrossRefGoogle Scholar
[10]Kay, S.M., Fundamentals of Statistical Signal Processing: Estimation Theory, Pearson (2011).Google Scholar
[11]Agilent Technologies, Fundamentals of the Electronic Counters.Google Scholar
[12]Verdun, F.R., Giancaspro, C., and Marshall, A.G., Applied Spectroscopy, 42, 715 (1988).Google Scholar