Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Zhang, Zhi-Dong
2013.
Mathematical structure of the three-dimensional (3D) Ising model.
Chinese Physics B,
Vol. 22,
Issue. 3,
p.
030513.
March, N. H.
and
Zhang, Z. D.
2013.
Theory and phenomenology for a variety of classical and quantum phase transitions.
Journal of Mathematical Chemistry,
Vol. 51,
Issue. 7,
p.
1694.
Brics, Martins
Kaupužs, Jevgenijs
and
Mahnke, Reinhard
2013.
Scaling behavior of an airplane-boarding model.
Physical Review E,
Vol. 87,
Issue. 4,
Zhang, Z.D.
2017.
The nature of three dimensions: Non-local behavior in the three-dimensional (3D) Ising model.
Journal of Physics: Conference Series,
Vol. 827,
Issue. ,
p.
012001.
Kaupužs, J.
Melnik, R. V. N.
and
Rimšāns, J.
2017.
Corrections to finite-size scaling in the 3D Ising model based on nonperturbative approaches and Monte Carlo simulations.
International Journal of Modern Physics C,
Vol. 28,
Issue. 04,
p.
1750044.
Suzuki, Osamu
and
Zhang, Zhidong
2021.
A Method of Riemann–Hilbert Problem for Zhang’s Conjecture 1 in a Ferromagnetic 3D Ising Model: Trivialization of Topological Structure.
Mathematics,
Vol. 9,
Issue. 7,
p.
776.

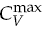 data suggests that
data suggests that 