Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-27T13:16:40.521Z Has data issue: false hasContentIssue false
  • English
  • Français

Space-Time Discontinuous Galerkin Method for Maxwell’s Equations

Published online by Cambridge University Press:  03 June 2015

Ziqing Xie ,
Bo Wang  and
Zhimin Zhang
Ziqing Xie*
Affiliation:
School of Mathematics and Computer Science, Guizhou Normal University, Guiyang, Guizhou 550001, China Key Laboratory of High Performance Computing and Stochastic Information Processing, Ministry of Education of China, Hunan Normal University, Changsha, Hunan 410081, China
Bo Wang*
Affiliation:
College of Mathematics and Computer Science, Hunan Normal University, Changsha, Hunan 410081, China Singapore-MIT Alliance, 4 Engineering Drive 3, National University of Singapore, Singapore 117576, Singapore
Zhimin Zhang*
Affiliation:
Department of Mathematics, Wayne State University, Detroit, MI 48202, USA Guangdong Province Key Laboratory of Computational Science, School of Mathematics and Computational Science, Sun Yat-sen University, Guangzhou, 510275, China
*
Email:ziqingxie@yahoo.com.cn
Corresponding author.Email:bowanghn@gmail.com
Email:ag7761@wayne.edu
Get access

Abstract

A fully discrete discontinuous Galerkin method is introduced for solving time-dependent Maxwell’s equations. Distinguished from the Runge-Kutta discontinuous Galerkin method (RKDG) and the finite element time domain method (FETD), in our scheme, discontinuous Galerkin methods are used to discretize not only the spatial domain but also the temporal domain. The proposed numerical scheme is proved to be unconditionally stable, and a convergent rate is established under the L2-norm when polynomials of degree atmost r and k are used for temporal and spatial approximation, respectively. Numerical results in both 2-D and 3-D are provided to validate the theoretical prediction. An ultra-convergence of order 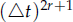in time step is observed numerically for the numerical fluxes w.r.t. temporal variable at the grid points.

Keywords

35Q6165M1265M6065N12Discontinuous Galerkin methodMaxwell’s equationsfull-discretization L2-error estimateL2-stabilityultra-convergence
Type
Research Article
Information
Communications in Computational Physics , Volume 14 , Issue 4 , October 2013 , pp. 916 - 939
Copyright
Copyright © Global Science Press Limited 2013

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Argyris, J. H. and Scharpf, D. W., Finite elements in time and space, Nucl. Engrg. Des., 10 (1969), 456–464.Google Scholar
[2]Boffi, D., Fernandes, P., Gastaldi, L., and Perugia, I., Computational models of electromagnetic resonators: analysis of edge element approximation, SIAM J. Numer. Anal., 36 (1999), 1264–1290.Google Scholar
[3]Bonnerot, R. and Jamet, P., Numerical computation of the free boundary for the two-dimensional Stefan problem by space-time finite elements, J. Comput. Phys., 25 (1977), 163–181.Google Scholar
[4]Buffa, A., Remarks on the discretization of some noncoercive operator with applications to heterogeneous Maxwell equations, SIAM J. Numer. Anal., 43 (2005), 1–18.Google Scholar
[5]Bruch, J. C. and Zyvoloski, G., Transient two-dimensional heat conduction problems solved by the finite element method, Internat. J. Numer. Methods Engrg., 8 (1974), 481–494.Google Scholar
[6]Castillo, P., Cockburn, B., Schötzau, D. and Schwab, C., Optimal a priori error estimates for the hp-version of the local discontinuous Galerkin method for convection-diffusion problems, Math. Comput., 71 (2001), 455–478.Google Scholar
[7]Chen, C. M., Structure theory of superconvergence of finite elements, Hunan Science and Technology Press, Changsha, China (in Chinese), 2001.Google Scholar
[8]Chen, M. H., Cockburn, B., and Reitich, F., High-order RKDG methods for computational electromagnetics, J. Sci. Comput., 22–23 (2005), 205–226.Google Scholar
[9]Ciarlet, P. Jr and Zou, J., Fully discretefinite element approaches for time-dependent Maxwell equations, Numer. Math., 82 (1999), 193–219.Google Scholar
[10]Cialet, P., The finite element method for elliptic problems, North Holland, 1978.Google Scholar
[11]Cockburn, B., Li, F., and Shu, C. W., Locally divergence-free discontinuous Galerkin methods for the Maxwell equations, J. Comput. Phys., 194 (2004), 588–610.Google Scholar
[12]Cockburn, B. and Shu, C. W., Runge-Kutta Discontinuous Galerkin methods for time-depedent convection-diffusion systems, SIAM J. Numer. Anal., 35 (1998), 2440–2463.Google Scholar
[13]Douglas, T., Dupont, T., and Wheeler, M. F., An L ∞ estimate and superconvergence result for a Galerkin method for elliptic equations based on tensor products of piecewise polynomials, RAIRO Anal. Numer., 8 (1974), 61–66.Google Scholar
[14]Gao, L. P. and Liang, D., New energy-conserved identities and super-convergence of the symmetric EC-S-FDTD scheme for Maxwell’s equations in 2D, Commun. Comput. Phys., 11 (2012), 1673–1696.Google Scholar
[15]Hesthaven, J. S. and Warburton, T., Nodal high-order methods on unstructured grids, I: Timedomain solution of Maxwell equations, J. Comput. Phys., 181 (2002), 186–221.Google Scholar
[16]Hughes, T. J. R. and Hulbert, G. M., Space-time finite element methods for elastodynamics: formulations and error estimates, Comput. Methods Appl. Mech. Engrg., 66 (1988), 339–363.Google Scholar
[17]Hulbert, G. M. and Hughes, T. J. R., Space-time finite element methods for second-order hyperbolic equations, Comput. Methods Appl. Mech. Engrg., 84 (1990), 327–348.Google Scholar
[18]Johnson, C., Error estimates and automatic time step control for numerical methods for stiff ordinary differential equations, Technical Report 1984-27, Department of Mathematics, Chalmers University of Technology and University of Göteborg, Göteborg, Sweden, 1984.Google Scholar
[19]Lesaint, P. and Raviart, P. A., On a finite elment method for solving the neutron transport equation, in: deBoor, C. ed., Mathematical Aspects of Finite Elements in Partial Differential Equations (Academic Press, New York, 1974), 89–123.Google Scholar
[20]Li, J., Error analysis of finite element methods for 3-D Maxwell’s equations in dispersive media, J. Comput. Appl. Math., 188 (2006), 107–120.Google Scholar
[21]Li, J., Error analysis of fully discrete mixed finite element schemes for 3-D Maxwell’s equations in dispersive media, Comput. Methods Appl. Mech. Engrg., 196 (2007), 3081–3094.Google Scholar
[22]Li, J. and Chen, Y., Analysis of a time-domain finite element method for 3-D Maxwell’s equations in dispersive media, Comput. Methods Appl. Mech. Engrg., 195 (2006), 4220–4229.Google Scholar
[23]Li, J., Optimal L 2 error estimates for the interior penalty DG method for Maxwell’s equations in cold plasma, Commun. Comput. Phys. 11 (2012), 319–334.Google Scholar
[24]Lu, T., Zhang, P., and Cai, W., Discontinuous Galerkin methods for dispersive and lossy Maxwell’s equations and PML boundary conditions, J. Comput. Phys., 200 (2004), 549–580.CrossRefGoogle Scholar
[25]Ma, C. F., Finite-element method for time-dependent Maxwell’s equations based on an explicit-magnetic-field scheme, J. Comput. and Appl. Math., 194 (2006), 409–424.Google Scholar
[26]Makridakis, C. G. and Monk, P., Time-discrete finite element schemes for Maxwell’s equations. RAIRO Math. Modeling Numer. Anal., 29 (1995), 171–197.Google Scholar
[27]Monk, P., Anlysis of a finite element method for Maxwell’s equations, SIAM J. Numer. Anal, 29 (1992), 714–729.CrossRefGoogle Scholar
[28]Monk, P., A finite element methods for approximating the time-harmonic Maxwell equations, Numer. Math., 63 (1992), 243–261.Google Scholar
[29]Monk, P. and Richter, G. R., A Discontinuous Galerkin Method for Linear Symmetric Hyperbolic Systems in Inhomogeneous Media, J. Sci. Comput., 22–23 (2005), 443–477.Google Scholar
[30]Oden, J. T., A general theory of finite elements II: Applications, Internat. J. Numer. Methods in Engrg., 1 (1969), 247–259.Google Scholar
[31]Reed, W. H. and Hill, T. R., Triangular mesh methods for the neutron transport equation, Report LA-UR-73479, Los Alamos Scientific Laboratory, Los Alamos, 1973.Google Scholar
[32]Richter, G. R., An explicit finite element method for the wave equation, Appl. Numer. Math., 16 (1994), 65–80Google Scholar
[33]Tu, S. Z., Skelton, G. W., and Pang, Q., Extension of the high-order space-time discontinuous Galerkin cell vertex scheme to solve time dependent diffusion equations, Commun. Comput. Phys., 11 (2012), 1503–1524.Google Scholar
[34]Wang, B., Xie, Z. Q., and Zhang, Z., Error analysis of a discontinuous Galerkin method for Maxwell equations in dispersive media, J. Comput. Phys., 229 (2010), 8552–8563.Google Scholar