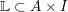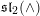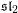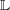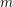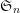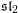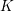Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Zhang, Melissa
2018.
A rank inequality for the annular Khovanov
homology of 2–periodic links.
Algebraic & Geometric Topology,
Vol. 18,
Issue. 2,
p.
1147.
Feller, Peter
and
Hubbard, Diana
2019.
Braids with as many full twists as strands realize the braid index.
Journal of Topology,
Vol. 12,
Issue. 4,
p.
1069.
Akhmechet, Rostislav
Krushkal, Vyacheslav
and
Willis, Michael
2021.
Stable homotopy refinement of quantum annular homology.
Compositio Mathematica,
Vol. 157,
Issue. 4,
p.
710.
EHRIG, M.
and
TUBBENHAUER, D.
2021.
RELATIVE CELLULAR ALGEBRAS.
Transformation Groups,
Vol. 26,
Issue. 1,
p.
229.
Truong, Linh
and
Zhang, Melissa
2022.
Annular Link Invariants from the Sarkar–Seed–Szabó Spectral Sequence.
Michigan Mathematical Journal,
Vol. 71,
Issue. 4,
SAUNDERS, N.
and
WILBERT, A.
2022.
EXOTIC SPRINGER FIBERS FOR ORBITS CORRESPONDING TO ONE-ROW BIPARTITIONS.
Transformation Groups,
Vol. 27,
Issue. 3,
p.
1111.
Anno, Rina
and
Nandakumar, Vinoth
2022.
Exotic t-structures for two-block Springer fibres.
Transactions of the American Mathematical Society,
Vol. 376,
Issue. 3,
p.
1523.
Manolescu, Ciprian
and
Neithalath, Ikshu
2022.
Skein lasagna modules for 2-handlebodies.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2022,
Issue. 788,
p.
37.
Khovanov, Mikhail
and
Lipshitz, Robert
2022.
Categorical lifting of the Jones polynomial: a survey.
Bulletin of the American Mathematical Society,
Vol. 60,
Issue. 4,
p.
483.
Akhmechet, Rostislav
Krushkal, Vyacheslav
and
Willis, Michael
2022.
Towards an sl2 action on the annular Khovanov spectrum.
Advances in Mathematics,
Vol. 408,
Issue. ,
p.
108581.
Manolescu, Ciprian
Walker, Kevin
and
Wedrich, Paul
2023.
Skein lasagna modules and handle decompositions.
Advances in Mathematics,
Vol. 425,
Issue. ,
p.
109071.
Morrison, Scott
Walker, Kevin
and
Wedrich, Paul
2023.
Invariants of 4–manifolds from Khovanov–Rozansky
link homology.
Geometry & Topology,
Vol. 26,
Issue. 8,
p.
3367.
Akhmechet, Rostislav
and
Khovanov, Mikhail
2023.
Anchored foams and annular homology.
Algebraic & Geometric Topology,
Vol. 23,
Issue. 7,
p.
3129.
Gorsky, Eugene
and
Wedrich, Paul
2023.
Evaluations of annular Khovanov–Rozansky homology.
Mathematische Zeitschrift,
Vol. 303,
Issue. 1,
Akhmechet, Rostislav
2023.
Equivariant annular Khovanov homology.
Journal of Knot Theory and Its Ramifications,
Vol. 32,
Issue. 02,
Binns, Fraser
and
Martin, Gage
2024.
Knot Floer homology, link Floer homology and link detection.
Algebraic & Geometric Topology,
Vol. 24,
Issue. 1,
p.
159.
Necheles, Casey
and
Wehrli, Stephan
2024.
Odd annular Bar-Natan category and 𝔤𝔩(1|1).
Journal of Knot Theory and Its Ramifications,
Vol. 33,
Issue. 08,
Stoffregen, Matthew
and
Zhang, Melissa
2024.
Localization in Khovanov homology.
Geometry & Topology,
Vol. 28,
Issue. 4,
p.
1501.
Queffelec, Hoel
and
Wedrich, Paul
2024.
Extremal weight projectors II, 𝔤𝔩 N case.
Algebraic Combinatorics,
Vol. 7,
Issue. 1,
p.
187.
Lipshitz, Robert
and
Sarkar, Sucharit
2024.
Frontiers in Geometry and Topology.
Vol. 109,
Issue. ,
p.
157.