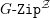Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Goldring, Wushi
and
Koskivirta, Jean-Stefan
2018.
Quasi-constant characters: Motivation, classification and applications.
Advances in Mathematics,
Vol. 339,
Issue. ,
p.
336.
Goldring, Wushi
2019.
The Griffiths bundle is generated by groups.
Mathematische Annalen,
Vol. 375,
Issue. 3-4,
p.
1283.
Goldring, Wushi
and
Koskivirta, Jean-Stefan
2019.
Strata Hasse invariants, Hecke algebras and Galois representations.
Inventiones mathematicae,
Vol. 217,
Issue. 3,
p.
887.
Goldring, Wushi
2020.
Quasi-constant fundamental weights in terms of Levi Weyl groups.
Journal of Algebra,
Vol. 559,
Issue. ,
p.
87.
Imai, Naoki
and
Koskivirta, Jean-Stefan
2021.
Automorphic vector bundles on the stack ofG-zips.
Forum of Mathematics, Sigma,
Vol. 9,
Issue. ,
Diamond, Fred
and
Kassaei, Payman L
2023.
The Cone of Minimal Weights for Mod p Hilbert Modular Forms.
International Mathematics Research Notices,
Vol. 2023,
Issue. 14,
p.
12148.
Cooper, Simon
2024.
Tautological rings of Hilbert modular varieties.
Mathematische Zeitschrift,
Vol. 308,
Issue. 1,
Imai, Naoki
and
Koskivirta, Jean-Stefan
2024.
Partial Hasse invariants for Shimura varieties of Hodge-type.
Advances in Mathematics,
Vol. 440,
Issue. ,
p.
109518.