Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-26T08:06:44.931Z Has data issue: false hasContentIssue false
  • English
  • Français

Correlations of multiplicative functions and applications

Part of: Exponential sums and character sums

Published online by Cambridge University Press:  31 May 2017

Oleksiy Klurman
Oleksiy Klurman*
Affiliation:
Départment de Mathématiques et de Statistique, Université de Montréal, CP 6128, succ. Centre-ville, Montréal, QC H3C 3J7, Canada email lklurman@gmail.com Department of Mathematics, University College London, Gower Street, London WC1E 6BT, UK
Get access Rights & Permissions [Opens in a new window]

Abstract

We give an asymptotic formula for correlations

$$\begin{eqnarray}\mathop{\sum }_{n\leqslant x}f_{1}(P_{1}(n))f_{2}(P_{2}(n))\cdots f_{m}(P_{m}(n)),\end{eqnarray}$$
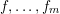where $f,\ldots ,f_{m}$ are bounded ‘pretentious’ multiplicative functions, under certain natural hypotheses. We then deduce several desirable consequences. First, we characterize all multiplicative functions 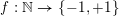$f:\mathbb{N}\rightarrow \{-1,+1\}$ with bounded partial sums. This answers a question of Erdős from 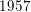$1957$ in the form conjectured by Tao. Second, we show that if the average of the first divided difference of the multiplicative function is zero, then either 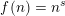$f(n)=n^{s}$ for 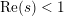$\operatorname{Re}(s)<1$ or 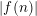$|f(n)|$ is small on average. This settles an old conjecture of Kátai. Third, we apply our theorem to count the number of representations of 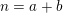$n=a+b$, where 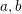$a,b$ belong to some multiplicative subsets of 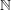$\mathbb{N}$. This gives a new ‘circle method-free’ proof of a result of Brüdern.

Keywords

multiplicative functionsDelange’s theoremcorrelations

MSC classification

Primary: 11L40: Estimates on character sums
Type
Research Article
Information
Compositio Mathematica , Volume 153 , Issue 8 , August 2017 , pp. 1622 - 1657
Copyright
© The Author 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Brüdern, J., Binary additive problems and the circle method, multiplicative sequences and convergent sieves , in Analytic number theory (Cambridge University Press, Cambridge, 2009), 91–132.Google Scholar
Elliott, P. D. T. A., On the correlation of multiplicative functions , Notas Soc. Mat. Chile 11 (1992), 1–11.Google Scholar
Erdős, P., On the distribution function of additive functions , Ann. of Math. (2) 47 (1946), 1–20.Google Scholar
Erdős, P., Some unsolved problems , Michigan Math. J. 4 (1957), 291–300.Google Scholar
Erdős, P., On some of my problems in number theory I would most like to see solved , in Number theory (Ootacamund, 1984), Lecture Notes in Mathematics, vol. 1122 (Springer, Berlin, 1985), 74–84.CrossRefGoogle Scholar
Erdős, P., Some applications of probability methods to number theory , in Mathematical statistics and applications, Vol. B (Bad Tatzmannsdorf, 1983) (Reidel, Dordrecht, 1985), 1–18.Google Scholar
Granville, A. and Soundararajan, K., Large character sums: pretentious characters and the Pólya–Vinogradov theorem , J. Amer. Math. Soc. 20 (2007), 357–384.CrossRefGoogle Scholar
Granville, A. and Soundararajan, K., Sieving and the Erdős–Kac theorem , in Equidistribution in number theory, an introduction, NATO Science Series II: Mathematics, Physics and Chemistry, vol. 237 (Springer, Dordrecht, 2007), 15–27.Google Scholar
Halász, G., On the distribution of additive and the mean values of multiplicative arithmetic functions , Studia Sci. Math. Hungar. 6 (1971), 211–233.Google Scholar
Halász, G., On the distribution of additive arithmetic functions , Acta Arith. 27 (1975), 143–152; collection of articles in memory of Juriĭ Vladimirovič Linnik.CrossRefGoogle Scholar
Hildebrand, A., An Erdős–Wintner theorem for differences of additive functions , Trans. Amer. Math. Soc. 310 (1988), 257–276.Google Scholar
Hildebrand, A., Multiplicative functions at consecutive integers. II , Math. Proc. Cambridge Philos. Soc. 103 (1988), 389–398.Google Scholar
Kátai, I., On a problem of P. Erdős , J. Number Theory 2 (1970), 1–6.Google Scholar
Kátai, I., Some problems in number theory , Studia Sci. Math. Hungar. 16 (1983), 289–295.Google Scholar
Kátai, I., Multiplicative functions with regularity properties. VI , Acta Math. Hungar. 58 (1991), 343–350.Google Scholar
Kátai, I., Continuous homomorphisms as arithmetical functions, and sets of uniqueness , in Number theory, Trends in Mathematics (Birkhäuser, Basel, 2000), 183–200.Google Scholar
Matomäki, K. and Radziwiłł, M., Multiplicative functions in short intervals , Ann. of Math. (2) 183 (2016), 1015–1056.Google Scholar
Matomäki, K., Radziwiłł, M. and Tao, T., An averaged form of Chowla’s conjecture , Algebra Number Theory 9 (2015), 2167–2196.Google Scholar
Mauclaire, J.-L. and Murata, L., On the regularity of arithmetic multiplicative functions. I , Proc. Japan Acad. Ser. A Math. Sci. 56 (1980), 438–440.Google Scholar
Phong, B., A characterization of some unimodular multiplicative functions , Publ. Math. Debrecen 57 (2000), 339–366.Google Scholar
Phong, B. M., Additive functions at consecutive integers , Acta Math. Hungar. 142 (2014), 260–274.CrossRefGoogle Scholar
Stepanauskas, G., The mean values of multiplicative functions. V , in Analytic and probabilistic methods in number theory (Palanga, 2001) (TEV, Vilnius, 2002), 272–281.Google Scholar
Tao, T., The Erdős discrepancy problem , Discrete Anal. 1 (2016), 27pp, arXiv:1509.05363.Google Scholar
Tao, T., The logarithmically averaged Chowla and Elliott conjectures for two-point correlations , Forum Math. Pi 4 (2016), 36pp.CrossRefGoogle Scholar
Wirsing, E., Tang, Y. and Shao, P., On a conjecture of Kátai for additive functions , J. Number Theory 56 (1996), 391–395.CrossRefGoogle Scholar
Wirsing, E. and Zagier, D., Multiplicative functions with difference tending to zero , Acta Arith. 100 (2001), 75–78.Google Scholar