No CrossRef data available.
Article contents
Cycles in the de Rham cohomology of abelian varieties over number fields
Published online by Cambridge University Press: 08 March 2018
Abstract
In his 1982 paper, Ogus defined a class of cycles in the de Rham cohomology of smooth proper varieties over number fields. This notion is a crystalline analogue of 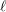 $\ell$ -adic Tate cycles. In the case of abelian varieties, this class includes all the Hodge cycles by the work of Deligne, Ogus, and Blasius. Ogus predicted that such cycles coincide with Hodge cycles for abelian varieties. In this paper, we confirm Ogus’ prediction for some families of abelian varieties. These families include geometrically simple abelian varieties of prime dimension that have non-trivial endomorphism ring. The proof uses a crystalline analogue of Faltings’ isogeny theorem due to Bost and the known cases of the Mumford–Tate conjecture.
$\ell$ -adic Tate cycles. In the case of abelian varieties, this class includes all the Hodge cycles by the work of Deligne, Ogus, and Blasius. Ogus predicted that such cycles coincide with Hodge cycles for abelian varieties. In this paper, we confirm Ogus’ prediction for some families of abelian varieties. These families include geometrically simple abelian varieties of prime dimension that have non-trivial endomorphism ring. The proof uses a crystalline analogue of Faltings’ isogeny theorem due to Bost and the known cases of the Mumford–Tate conjecture.
Information
- Type
- Research Article
- Information
- Copyright
- © The Author 2018

