Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T03:57:44.427Z Has data issue: false hasContentIssue false
  • English
  • Français

Discrepancy in modular arithmetic progressions

Part of: Probabilistic theory: distribution modulo $1$; metric theory of algorithms Extremal combinatorics Elementary number theory Sequences and sets

Published online by Cambridge University Press:  01 December 2022

Jacob Fox ,
Max Wenqiang Xu  and
Yunkun Zhou
Jacob Fox
Affiliation:
Department of Mathematics, Stanford University, Stanford, CA, USA jacobfox@stanford.edu
Max Wenqiang Xu
Affiliation:
Department of Mathematics, Stanford University, Stanford, CA, USA maxxu@stanford.edu
Yunkun Zhou
Affiliation:
Department of Mathematics, Stanford University, Stanford, CA, USA yunkunzhou@stanford.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Celebrated theorems of Roth and of Matoušek and Spencer together show that the discrepancy of arithmetic progressions in the first 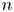$n$ positive integers is 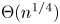$\Theta (n^{1/4})$. We study the analogous problem in the 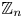$\mathbb {Z}_n$ setting. We asymptotically determine the logarithm of the discrepancy of arithmetic progressions in 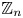$\mathbb {Z}_n$ for all positive integer 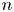$n$. We further determine up to a constant factor the discrepancy of arithmetic progressions in 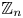$\mathbb {Z}_n$ for many 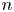$n$. For example, if 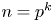$n=p^k$ is a prime power, then the discrepancy of arithmetic progressions in 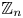$\mathbb {Z}_n$ is 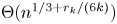$\Theta (n^{1/3+r_k/(6k)})$, where 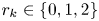$r_k \in \{0,1,2\}$ is the remainder when 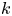$k$ is divided by 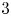$3$. This solves a problem of Hebbinghaus and Srivastav.

Keywords

discrepancycongruencearithmetic progressionpartial coloring methodFourier analysis

MSC classification

Primary: 11K38: Irregularities of distribution, discrepancy 11B25: Arithmetic progressions 11A07: Congruences; primitive roots; residue systems 11B30: Arithmetic combinatorics; higher degree uniformity 05D40: Probabilistic methods
Secondary: 05D10: Ramsey theory 11A25: Arithmetic functions; related numbers; inversion formulas 11B50: Sequences (mod $m$)
Type
Research Article
Information
Compositio Mathematica , Volume 158 , Issue 11 , November 2022 , pp. 2082 - 2108
Check for updates
Copyright
© 2022 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Fox is supported by a Packard Fellowship and by NSF Awards DMS-1800053 and DMS-2154169. Xu is supported by the Cuthbert C. Hurd Graduate Fellowship in the Mathematical Sciences, Stanford. Zhou is supported by NSF GRFP Grant DGE-1656518.

References

Alon, N. and Spencer, J. H., The probabilistic method, fourth edition (Wiley, Hoboken, NJ, 2016).Google Scholar
Beck, J., Roth's estimate of the discrepancy of integer sequences is nearly sharp, Combinatorica 1 (1981), 319–325.CrossRefGoogle Scholar
Beck, J. and Chen, W. W. L., Irregularities of distribution, Cambridge Tracts in Mathematics, vol. 89 (Cambridge University Press, Cambridge, 1987).CrossRefGoogle Scholar
Chazelle, B., The discrepancy method: randomness and complexity (Cambridge University Press, New York, 2000).CrossRefGoogle Scholar
Chen, W., Srivastav, A. and Travaglini, G., eds., A panorama of discrepancy theory, Lecture Notes in Mathematics, vol. 2107 (Springer, 2014).CrossRefGoogle Scholar
Erdös, P. and Sárközy, A., Some solved and unsolved problems in combinatorial number theory, Math. Slovaca 28 (1978), 407–421.Google Scholar
Hardy, G. H. and Wright, E. M., An introduction to the theory of numbers, sixth edition (Oxford University Press, Oxford, 2008).Google Scholar
Hebbinghaus, N. and Srivastav, A., Discrepancy of (centered) arithmetic progressions in $\mathbb {Z}_p$, European J. Combin. 35 (2014), 324–334.CrossRefGoogle Scholar
Landau, E., Ueber die zahlentheoretische Funktion $\phi (n)$ und ihre Beziehung zum Goldbachschen Satz, Nachr. Ges. Wiss. Göttingen Math. Phys. Klasse 1900 (1900), 177–186.Google Scholar
Lovett, S. and Meka, R., Constructive discrepancy minimization by walking on the edges, SIAM J. Comput. 44 (2015), 1573–1582.CrossRefGoogle Scholar
Matoušek, J., Geometric discrepancy: an illustrated guide, Algorithms and Combinatorics, vol. 18 (Springer, Berlin, 1999).CrossRefGoogle Scholar
Matoušek, J. and Spencer, J., Discrepancy in arithmetic progressions, J. Amer. Math. Soc. 9 (1996), 195–204.CrossRefGoogle Scholar
Roth, K. F., Remark concerning integer sequences, Acta Arith. 9 (1964), 257–260.CrossRefGoogle Scholar
Tao, T., The Erdös discrepancy problem, Discrete Anal. 2016 (2016), 1.Google Scholar
Weyl, H., Über die Gleichverteilung von Zahlen mod. Eins., Math. Ann. 77 (1916), 313–352 (in German).CrossRefGoogle Scholar