Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-10T21:12:26.571Z Has data issue: false hasContentIssue false
  • English
  • Français

The distribution of the maximum of partial sums of Kloosterman sums and other trace functions

Part of: Exponential sums and character sums Limit theorems (Co)homology theory Finite fields and commutative rings (number-theoretic aspects)

Published online by Cambridge University Press:  28 June 2021

Pascal Autissier ,
Dante Bonolis  and
Youness Lamzouri
Pascal Autissier
Affiliation:
I.M.B., Université de Bordeaux, 351, cours de la Libération, 33405Talence, Francepascal.autissier@math.u-bordeaux.fr
Dante Bonolis
Affiliation:
IST Austria, Am Campus 1, 3400Klosterneuburg, Austriadante.bonolis@ist.ac.at
Youness Lamzouri
Affiliation:
Institut Élie Cartan de Lorraine, Université de Lorraine, BP 70239, 54506Vandoeuvre-lès-Nancy Cedex, France and youness.lamzouri@univ-lorraine.fr Department of Mathematics and Statistics, York University, 4700 Keele Street, Toronto, ONM3J1P3, Canada
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we investigate the distribution of the maximum of partial sums of families of 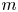$m$-periodic complex-valued functions satisfying certain conditions. We obtain precise uniform estimates for the distribution function of this maximum in a near-optimal range. Our results apply to partial sums of Kloosterman sums and other families of 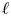$\ell$-adic trace functions, and are as strong as those obtained by Bober, Goldmakher, Granville and Koukoulopoulos for character sums. In particular, we improve on the recent work of the third author for Birch sums. However, unlike character sums, we are able to construct families of 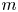$m$-periodic complex-valued functions which satisfy our conditions, but for which the Pólya–Vinogradov inequality is sharp.

MSC classification

Primary: 11L03: Trigonometric and exponential sums, general
Secondary: 11T23: Exponential sums 14F20: Étale and other Grothendieck topologies and (co)homologies 60F10: Large deviations
Type
Research Article
Information
Compositio Mathematica , Volume 157 , Issue 7 , July 2021 , pp. 1610 - 1651
Check for updates
Copyright
© 2021 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The third author is partially supported by a Discovery Grant from the Natural Sciences and Engineering Research Council of Canada.

References

Birch, B. J., How the number of points of an elliptic curve over a fixed prime field varies, J. Lond. Math. Soc. (2) 43 (1968), 57–60.CrossRefGoogle Scholar
Bober, J., Goldmakher, L., Granville, A. and Koukoulopoulos, D., The frequency and the structure of large character sums, J. Eur. Math. Soc. (JEMS) 20 (2018), 1759–1818.CrossRefGoogle Scholar
Bonolis, D., On the size of the maximum of incomplete Kloosterman sums, Math. Proc. Cambridge Philos. Soc. (2021), doi:10.1017/S030500412100030X.CrossRefGoogle Scholar
Conrey, B., Notes on eigenvalue distributions for the classical compact groups, in Recent perspectives in random matrix theory and number theory, London Mathematical Society Lecture Note Series, vol. 322 (Cambridge University Press, 2005), 111–145.CrossRefGoogle Scholar
Deligne, P., Cohomologie étale (SGA $4\frac {1}2$), Lecture Notes in Mathematics, vol. 569 (Springer, 1977).Google Scholar
Deligne, P., La conjecture de Weil. II, Publ. Math. Inst. Hautes Études Sci. 52 (1980), 137–252.CrossRefGoogle Scholar
Fouvry, É., Kowalski, E. and Michel, P., Counting sheaves using spherical codes, Math. Res. Lett. 20 (2013), 305–323.CrossRefGoogle Scholar
Fouvry, É., Kowalski, E. and Michel, P., Trace functions over finite fields and their applications, in Colloquium De Giorgi 2013 and 2014, Colloquia, vol. 5 (Ed. Norm., Pisa, 2014), 7–35.Google Scholar
Fouvry, É., Kowalski, E. and Michel, P., Algebraic twists of modular forms and Hecke orbits, Geom. Funct. Anal. 25 (2015), 580–657.CrossRefGoogle Scholar
Fouvry, É., Kowalski, E. and Michel, P., A study in sums of products, Philos. Trans. Roy. Soc. A 373 (2015), 20140309.Google Scholar
Fouvry, É., Kowalski, E. and Michel, P., On the conductor of cohomological transforms, Preprint (2020), arXiv:1310.3603.Google Scholar
Fouvry, E., Kowalski, E., Michel, P., Raju, C. S., Rivat, J. and Soundararajan, K., On short sums of trace functions, Ann. Inst. Fourier (Grenoble) 67 (2017), 423–449.CrossRefGoogle Scholar
Iwaniec, H. and Kowalski, E., Analytic number theory, American Mathematical Society Colloquium Publications, vol. 53 (American Mathematical Society, Providence, RI, 2004).Google Scholar
Katz, N. M., Sommes exponentielles, Astérisque 79 (1980), 1–209.Google Scholar
Katz, N. M., Gauss sums, Kloosterman sums, and monodromy groups, Annals of Mathematics Studies, vol. 116 (Princeton University Press, 1988).CrossRefGoogle Scholar
Katz, N. M., Exponential sums and differential equations, Annals of Mathematics Studies, vol. 124 (Princeton University Press, 1990).CrossRefGoogle Scholar
Katz, N. M., Rigid local systems, Annals of Mathematics Studies, vol. 139 (Princeton University Press, 1996).CrossRefGoogle Scholar
Katz, N. M., Convolution and equidistribution, Annals of Mathematics Studies, vol. 180 (Princeton University Press, 2012).Google Scholar
Kowalski, E. and Sawin, W., Kloosterman paths and the shape of exponential sums, Compos. Math. 152 (2016), 1489–1516.CrossRefGoogle Scholar
Lamzouri, Y., On the distribution of the maximum of cubic exponential sums, J. Inst. Math. Jussieu 19 (2020), 1259–1286.CrossRefGoogle Scholar
Livné, R., The average distribution of cubic exponential sums, J. Reine Angew. Math. 375–376 (1987), 362–379.Google Scholar
Montgomery, H. L. and Vaughan, R. C., Exponential sums with multiplicative coefficients, Invent. Math. 43 (1977), 69–82.CrossRefGoogle Scholar
Paley, R. E. A. C., A theorem on characters, J. Lond. Math. Soc. 7 (1932), 28–32.CrossRefGoogle Scholar
Perret-Gentil, C., Gaussian distribution of short sums of trace functions over finite fields, Math. Proc. Cambridge Philos. Soc. 163 (2017), 385–422.CrossRefGoogle Scholar
Weil, A., On some exponential sums, Proc. Natl. Acad. Sci. USA 34 (1948), 204–207.CrossRefGoogle ScholarPubMed