Article contents
Dynamics on ℙ1: preperiodic points and pairwise stability
Published online by Cambridge University Press: 05 January 2024
Abstract
DeMarco, Krieger, and Ye conjectured that there is a uniform bound B, depending only on the degree d, so that any pair of holomorphic maps 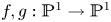 $f, g :{\mathbb {P}}^1\to {\mathbb {P}}^1$ with degree
$f, g :{\mathbb {P}}^1\to {\mathbb {P}}^1$ with degree 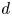 $d$ will either share all of their preperiodic points or have at most
$d$ will either share all of their preperiodic points or have at most 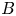 $B$ in common. Here we show that this uniform bound holds for a Zariski open and dense set in the space of all pairs,
$B$ in common. Here we show that this uniform bound holds for a Zariski open and dense set in the space of all pairs, 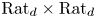 $\mathrm {Rat}_d \times \mathrm {Rat}_d$, for each degree
$\mathrm {Rat}_d \times \mathrm {Rat}_d$, for each degree 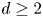 $d\geq 2$. The proof involves a combination of arithmetic intersection theory and complex-dynamical results, especially as developed recently by Gauthier and Vigny, Yuan and Zhang, and Mavraki and Schmidt. In addition, we present alternate proofs of the main results of DeMarco, Krieger, and Ye [Uniform Manin-Mumford for a family of genus 2 curves, Ann. of Math. (2) 191 (2020), 949–1001; Common preperiodic points for quadratic polynomials, J. Mod. Dyn. 18 (2022), 363–413] and of Poineau [Dynamique analytique sur
$d\geq 2$. The proof involves a combination of arithmetic intersection theory and complex-dynamical results, especially as developed recently by Gauthier and Vigny, Yuan and Zhang, and Mavraki and Schmidt. In addition, we present alternate proofs of the main results of DeMarco, Krieger, and Ye [Uniform Manin-Mumford for a family of genus 2 curves, Ann. of Math. (2) 191 (2020), 949–1001; Common preperiodic points for quadratic polynomials, J. Mod. Dyn. 18 (2022), 363–413] and of Poineau [Dynamique analytique sur 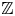 $\mathbb {Z}$ II : Écart uniforme entre Lattès et conjecture de Bogomolov-Fu-Tschinkel, Preprint (2022), arXiv:2207.01574 [math.NT]]. In fact, we prove a generalization of a conjecture of Bogomolov, Fu, and Tschinkel in a mixed setting of dynamical systems and elliptic curves.
$\mathbb {Z}$ II : Écart uniforme entre Lattès et conjecture de Bogomolov-Fu-Tschinkel, Preprint (2022), arXiv:2207.01574 [math.NT]]. In fact, we prove a generalization of a conjecture of Bogomolov, Fu, and Tschinkel in a mixed setting of dynamical systems and elliptic curves.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © 2024 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence
References
- 3
- Cited by


