Article contents
Equidistribution of Hodge loci II
Published online by Cambridge University Press: 12 January 2023
Abstract
Let 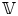 $\mathbb {V}$ be a polarized variation of Hodge structure over a smooth complex quasi-projective variety
$\mathbb {V}$ be a polarized variation of Hodge structure over a smooth complex quasi-projective variety 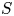 $S$. In this paper, we give a complete description of the typical Hodge locus for such variations. We prove that it is either empty or equidistributed with respect to a natural differential form, the pull–push form. In particular, it is always analytically dense when the pull–push form does not vanish. When the weight is two, the Hodge numbers are
$S$. In this paper, we give a complete description of the typical Hodge locus for such variations. We prove that it is either empty or equidistributed with respect to a natural differential form, the pull–push form. In particular, it is always analytically dense when the pull–push form does not vanish. When the weight is two, the Hodge numbers are 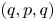 $(q,p,q)$ and the dimension of
$(q,p,q)$ and the dimension of 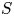 $S$ is least
$S$ is least 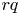 $rq$, we prove that the typical locus where the Picard rank is at least
$rq$, we prove that the typical locus where the Picard rank is at least 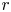 $r$ is equidistributed in
$r$ is equidistributed in 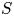 $S$ with respect to the volume form
$S$ with respect to the volume form 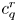 $c_q^r$, where
$c_q^r$, where 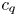 $c_q$ is the
$c_q$ is the 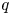 $q$th Chern form of the Hodge bundle. We obtain also several equidistribution results of the typical locus in Shimura varieties: a criterion for the density of the typical Hodge loci of a variety in
$q$th Chern form of the Hodge bundle. We obtain also several equidistribution results of the typical locus in Shimura varieties: a criterion for the density of the typical Hodge loci of a variety in 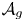 $\mathcal {A}_g$, equidistribution of certain families of CM points and equidistribution of Hecke translates of curves and surfaces in
$\mathcal {A}_g$, equidistribution of certain families of CM points and equidistribution of Hecke translates of curves and surfaces in  $\mathcal {A}_g$. These results are proved in the much broader context of dynamics on homogeneous spaces of Lie groups which are of independent interest. The pull–push form appears in this greater generality, we provide several tools to determine it, and we compute it in many examples.
$\mathcal {A}_g$. These results are proved in the much broader context of dynamics on homogeneous spaces of Lie groups which are of independent interest. The pull–push form appears in this greater generality, we provide several tools to determine it, and we compute it in many examples.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © 2023 The Author(s). The publishing rights in this article are licensed to Foundation Compositio Mathematica under an exclusive licence
References
- 8
- Cited by


