Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T08:01:36.720Z Has data issue: false hasContentIssue false
  • English
  • Français

Étale motives

Part of: (Co)homology theory Cycles and subschemes $K$-theory in geometry

Published online by Cambridge University Press:  24 September 2015

Denis-Charles Cisinski  and
Frédéric Déglise
Denis-Charles Cisinski
Affiliation:
Université Paul Sabatier, Institut de Mathématiques de Toulouse, Institut Universitaire de France, 118, route de Narbonne, 31062 Toulouse Cedex 9, France email denis-charles.cisinski@math.univ-toulouse.fr
Frédéric Déglise
Affiliation:
E.N.S. Lyon, UMPA, 46, allée d’Italie, 69364 Lyon Cedex 07, France email frederic.deglise@ens-lyon.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

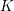We define a theory of étale motives over a noetherian scheme. This provides a system of categories of complexes of motivic sheaves with integral coefficients which is closed under the six operations of Grothendieck. The rational part of these categories coincides with the triangulated categories of Beilinson motives (and is thus strongly related to algebraic $K$-theory). We extend the rigidity theorem of Suslin and Voevodsky over a general base scheme. This can be reformulated by saying that torsion étale motives essentially coincide with the usual complexes of torsion étale sheaves (at least if we restrict ourselves to torsion prime to the residue characteristics). As a consequence, we obtain the expected results of absolute purity, of finiteness, and of Grothendieck duality for étale motives with integral coefficients, by putting together their counterparts for Beilinson motives and for torsion étale sheaves. Following Thomason’s insights, this also provides a conceptual and convenient construction of the 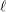$\ell$-adic realization of motives, as the homotopy 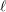$\ell$-completion functor.

Keywords

étale motivesh-topologyGrothendieck six functorsrigidity theoreml-adic realizationl-adic completion

MSC classification

Primary: 14F20: Étale and other Grothendieck topologies and (co)homologies 14F42: Motivic cohomology; motivic homotopy theory 14F05: Sheaves, derived categories of sheaves and related constructions 19E15: Algebraic cycles and motivic cohomology 14C25: Algebraic cycles
Type
Research Article
Information
Compositio Mathematica , Volume 152 , Issue 3 , March 2016 , pp. 556 - 666
Copyright
© The Authors 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ayoub, J., Les six opérations de Grothendieck et le formalisme des cycles évanescents dans le monde motivique (I, II), Astérisque 314, 315 (2007).Google Scholar
Ayoub, J., La réalisation étale et les opérations de Grothendieck, Ann. Sci. École Norm. Sup. (4) 47 (2014), 1–145.Google Scholar
Beilinson, A. A., Bernstein, J. and Deligne, P., Faisceaux pervers, Astérisque 100 (1982), 5–171.Google Scholar
Beilinson, A. A., Height pairing between algebraic cycles, in K-theory, arithmetic and geometry (Moscow, 1984–1986), Lecture Notes in Mathematics, vol. 1289 (Springer, Berlin, 1987), 1–25.Google Scholar
Bondarko, M. V., On weights for relative motives with integral coefficients, Preprint (2013),arXiv:1304.2335 [math.AG].Google Scholar
Bondarko, M. V., Weights for relative motives: relation with mixed complexes of sheaves, Int. Math. Res. Not. IMRN 2014 (2014), 4715–4767.Google Scholar
Balmer, P. and Schlichting, M., Idempotent completion of triangulated categories, J. Algebra 236 (2001), 819–834.CrossRefGoogle Scholar
Cisinski, D.-C., Descente par éclatements en K-théorie invariante par homotopie, Ann. of Math. (2) 177 (2013), 425–448.Google Scholar
Cisinski, D.-C. and Déglise, F., Local and stable homological algebra in Grothendieck abelian categories, Homology, Homotopy Appl. 11 (2009), 219–260.Google Scholar
Cisinski, D.-C. and Déglise, F., Triangulated categories of mixed motives, Preprint (2012),arXiv:0912.2110v3 [math.AG].Google Scholar
Cisinski, D.-C. and Déglise, F., Integral mixed motives in equal characteristic, Doc. Math. (2015), to appear, arXiv:1410.6359 [math.AG].Google Scholar
Conrad, B., Deligne’s notes on Nagata compactifications, J. Ramanujan Math. Soc. 22 (2007), 205–257.Google Scholar
Déglise, F., Finite correspondences and transfers over a regular base, in Algebraic cycles and motives, Vol. 1, London Mathematical Society Lecture Note Series, vol. 343 (Cambridge University Press, Cambridge, 2007), 138–205.Google Scholar
Déglise, F., Around the Gysin triangle II, Doc. Math. 13 (2008), 613–675.Google Scholar
Déglise, F., Motifs génériques, Rend. Semin. Mat. Univ. Padova 119 (2008), 173–244.Google Scholar
Déglise, F., Coniveau filtration and motives, in Regulators, Contemporary Mathematics, vol. 571 (American Mathematical Society, Providence, RI, 2012), 51–76.CrossRefGoogle Scholar
Déglise, F., Orientation theory in arithmetic geometry, Preprint (2014), http://perso.ens-lyon.fr/frederic.deglise/docs/2014/RR.pdf.Google Scholar
Deligne, P., Voevodsky lectures on cross functors, Notes, http://www.math.ias.edu/∼vladimir/seminar.html (2001).Google Scholar
Dwyer, W. G. and Greenlees, J. P. C., Complete modules and torsion modules, Amer. J. Math. 124 (2002), 199–220.Google Scholar
Grothendieck, A. and Dieudonné, J., Éléments de géométrie algébrique. II. Étude globale élémentaire de quelques classes de morphismes, Publ. Math. Inst. Hautes Études Sci. 8 (1961).Google Scholar
Grothendieck, A. and Dieudonné, J., Éléments de géométrie algébrique. IV. Étude locale des schémas et des morphismes de schémas IV, Publ. Math. Inst. Hautes Études Sci. 20, 24, 28, 32 (1964–1967).Google Scholar
Ekedahl, T., On the adic formalism, in The Grothendieck Festschrift, Vol. II, Progress in Mathematics, vol. 87 (Birkhäuser, Boston, MA, 1990), 197–218.Google Scholar
Fujiwara, K., A proof of the absolute purity conjecture (after Gabber), in Algebraic geometry 2000, Azumino (Hotaka), Advanced Studies in Pure Mathematics, vol. 36 (Mathematical Society of Japan, Tokyo, 2002), 153–183.Google Scholar
Geisser, T. and Levine, M., The K-theory of fields in characteristic p, Invent. Math. 139 (2000), 459–493.Google Scholar
Geisser, T. and Levine, M., The Bloch–Kato conjecture and a theorem of Suslin–Voevodsky, J. Reine Angew. Math. 530 (2001), 55–103.Google Scholar
Goodwillie, T. G. and Lichtenbaum, S., A cohomological bound for the h-topology, Amer. J. Math. 123 (2001), 425–443.Google Scholar
Hébert, D., Structure de poids à la Bondarko sur les motifs de Beilinson, Compos. Math. 147 (2011), 1447–1462.CrossRefGoogle Scholar
Hovey, M., Spectra and symmetric spectra in general model categories, J. Pure Appl. Algebra 165 (2001), 63–127.Google Scholar
Illusie, L., Lazslo, Y. and Orgogozo, F., Travaux de Gabber sur l’uniformisation locale et la cohomologie étale des schémas quasi-excellents, Astérisque 361, 362 (2014).Google Scholar
Jannsen, U., Continuous étale cohomology, Math. Ann. 280 (1988), 207–245.Google Scholar
Jannsen, U., Mixed motives and algebraic K-theory, Lecture Notes in Mathematics, vol. 1400 (Springer, Berlin, 1990).Google Scholar
Lichtenbaum, S., Values of zeta-functions at nonnegative integers, in Number theory, Noordwijkerhout 1983 (Noordwijkerhout, 1983), Lecture Notes in Mathematics, vol. 1068 (Springer, Berlin, 1984), 127–138.CrossRefGoogle Scholar
McCleary, J., A user’s guide to spectral sequences, Cambridge Studies in Advanced Mathematics, vol. 58, second edition (Cambridge University Press, Cambridge, 2001).Google Scholar
Mazza, C., Voevodsky, V. and Weibel, C., Lecture notes on motivic cohomology, Clay Mathematics Monographs, vol. 2 (American Mathematical Society, Providence, RI, 2006).Google Scholar
Morel, F., On the Friedlander–Milnor conjecture for groups of small rank, Current developments in mathematics, 2010 (International Press, Somerville, MA, 2011), 45–93.Google Scholar
Neeman, A., Triangulated categories, Annals of Mathematics Studies, vol. 148 (Princeton University Press, Princeton, NJ, 2001).CrossRefGoogle Scholar
Quillen, D., Higher algebraic K-theory, in Higher K-theories I (Proc. Conf., Battelle Memorial Inst., Seattle, WA, 1972), Lecture Notes in Mathematics, vol. 341 (Springer, 1973), 85–147.Google Scholar
Rosenschon, A. and Srinivas, V., Étale motivic cohomology and algebraic cycles, J. Inst. Math. Jussieu (2014), doi:10.1017/S1474748014000401.Google Scholar
Rydh, D., Submersions and effective descent of étale morphisms, Bull. Soc. Math. France 138 (2010), 181–230.CrossRefGoogle Scholar
Grothendieck, A. and Dieudonné, J., Revêtements étales et groupe fondamental, Documents mathématiques, vol. 3, édition recomposée et annotée (Société mathématique de France, Paris, 2003); Séminaire de Géométrie Algébrique du Bois–Marie 1960–61 (SGA 1), original edition published as Revêtements étales et groupe fondamental, Lecture Notes in Mathematics, vol. 224 (Springer, Berlin, 1971).Google Scholar
Artin, M., Grothendieck, A. and Verdier, J.-L., Théorie des topos et cohomologie étale des schémas, Lecture Notes in Mathematics, vols 269, 270, 305 (Springer, Berlin, 1972–1973); Séminaire de Géométrie Algébrique du Bois–Marie 1963–64 (SGA 4).Google Scholar
Deligne, P., Cohomologie étale, Lecture Notes in Mathematics, vol. 569 (Springer, Berlin, 1977); Séminaire de Géométrie Algébrique du Bois–Marie $\text{SGA}4{\textstyle \frac{1}{2}}$.Google Scholar
Grothendieck, A., Cohomologie ℓ-adique et fonctions L, Lecture Notes in Mathematics, vol. 589 (Springer, Berlin, 1977); Séminaire de Géométrie Algébrique du Bois–Marie 1965–66 (SGA 5).Google Scholar
Suslin, A. and Voevodsky, V., Singular homology of abstract algebraic varieties, Invent. Math. 123 (1996), 61–94.Google Scholar
Suslin, A. and Voevodsky, V., Bloch–Kato conjecture and motivic cohomology with finite coefficients, NATO Sciences Series, Series C: Mathematical and Physical Sciences, vol. 548 (Kluwer, Dordrecht, 2000), 117–189.Google Scholar
Suslin, A. and Voevodsky, V., Relative cycles and Chow sheaves, Annals of Mathematics Studies, vol. 143 (Princeton University Press, 2000), 10–86.Google Scholar
Voevodsky, V., Homology of schemes, Selecta Math. (N.S.) 2 (1996), 111–153.Google Scholar
Voevodsky, V., Motivic cohomology groups are isomorphic to higher Chow groups in any characteristic, Int. Math. Res. Not. IMRN 7 (2002), 351–355.Google Scholar
Voevodsky, V., On motivic cohomology with Z∕l-coefficients, Ann. of Math. (2) 174 (2011), 401–438.Google Scholar
Voevodsky, V., Suslin, A. and Friedlander, E. M., Cycles, transfers and motivic homology theories, Annals of Mathematics Studies, vol. 143 (Princeton University Press, 2000).Google Scholar