Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T09:22:54.700Z Has data issue: false hasContentIssue false
  • English
  • Français

Extensions de représentations de de Rham et vecteurs localement algébriques

Published online by Cambridge University Press:  03 March 2015

Gabriel Dospinescu
Gabriel Dospinescu*
Affiliation:
CNRS UMPA, École Normale Supérieure de Lyon, 46 allée d’Italie, 69007 Lyon, France email gabriel.dospinescu@ens-lyon.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 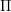${\rm\Pi}$ be an irreducible unitary completion of a locally algebraic 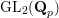$\text{GL}_{2}(\mathbf{Q}_{p})$-representation. We describe those first-order deformations of 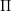${\rm\Pi}$ which are themselves completions of a locally algebraic representation. This answers a question of Paškūnas and has direct applications to the Breuil–Mézard conjecture.

Soit 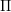${\rm\Pi}$ une complétion unitaire irréductible d’une représentation localement algébrique de 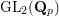$\text{GL}_{2}(\mathbf{Q}_{p})$. On décrit les déformations infinitésimales 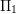${\rm\Pi}_{1}$ de 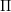${\rm\Pi}$ qui sont elles-mêmes complétions d’une représentation localement algébrique. Cela répond à une question de Paškūnas et a des applications directes à la conjecture de Breuil–Mézard.

Keywords

(𝜙, Γ)-moduleFontaine theoryp-adic local Langlands correspondenceadmissible Banach space representation
Type
Research Article
Information
Compositio Mathematica , Volume 151 , Issue 8 , August 2015 , pp. 1462 - 1498
Copyright
© The Author 2015 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Berger, L., Représentations p-adiques et équations différentielles, Invent. Math. 148 (2002), 219–284.CrossRefGoogle Scholar
Berger, L., Équations différentielles p-adiques et (𝜙, N)-modules filtrés, Astérisque 319 (2008), 13–38.Google Scholar
Berger, L. and Breuil, C., Sur quelques représentations potentiellement cristallines de G Qp, Astérisque 330 (2010), 155–211.Google Scholar
Bloch, S. and Kato, K., L-functions and Tamagawa numbers of motives, in The Grothendieck festschrift, Vol. I, Progress in Mathematics, vol. 86 (Birkhäuser, Boston, MA, 1990), 333–400.Google Scholar
Breuil, C., Invariant L et série spéciale p-adique, Ann. Sci. Éc. Norm. Supér. (4) 37 (2004), 559–610.CrossRefGoogle Scholar
Breuil, C. and Mézard, A., Multiplicités modulaires et représentations de GL2(Zp) et de Gal(Qp∕Qp) en l = p (avec un appendice par G. Henniart), Duke Math. J. 115 (2002), 205–310.Google Scholar
Breuil, C. and Mézard, A., Multiplicités modulaires raffinées, Bull. Soc. Math. France 142 (2014), 127–175.CrossRefGoogle Scholar
Cherbonnier, F. and Colmez, P., Représentations p-adiques surconvergentes, Invent. Math. 133 (1998), 581–611.CrossRefGoogle Scholar
Colmez, P., Théorie d’Iwasawa des représentations de de Rham d’un corps local, Ann. of Math. (2) 148 (1998), 485–571.CrossRefGoogle Scholar
Colmez, P., Espaces vectoriels de dimension finie et représentations de de Rham, Astérisque 319 (2008), 117–186.Google Scholar
Colmez, P., (𝜙, Γ)-modules et représentations du mirabolique de G, Astérisque 330 (2010), 61–153.Google Scholar
Colmez, P., Représentations de GL2(Qp) et (𝜙, Γ)-modules, Astérisque 330 (2010), 281–509.Google Scholar
Colmez, P., La série principale unitaire de $\text{GL}_{2}(\mathbf{Q}_{p})$: vecteurs localement analytiques, Proceedings of the Durham LMS Symposium (2011), to appear.Google Scholar
Colmez, P. and Dospinescu, G., Complétés universels de représentations de GL2(Qp), Algebra Number Theory 8 (2014), 1447–1519.CrossRefGoogle Scholar
Colmez, P., Dospinescu, G. and Paškūnas, V., The p-adic local Langlands correspondence for GL2(Qp), Cambridge J. Math. 2 (2014), 1–47.CrossRefGoogle Scholar
Colmez, P., Dospinescu, G. and Paškūnas, V., Irreducible components of deformation spaces: wild 2-adic exercises, Int. Math. Res. Not. IMRN 2014 (2014); doi:10.1093/imrn/rnu089.Google Scholar
Dospinescu, G., Actions infinitésimales dans la correspondance de Langlands locale p-adique pour GL2(Qp), Math. Ann. 354 (2012), 627–657.CrossRefGoogle Scholar
Dospinescu, G., Actions infinitésimales dans la correspondance de Langlands locale $p$-adique, PhD thesis, École Polytechnique (2012).CrossRefGoogle Scholar
Emerton, M., A local-global compatibility conjecture in the p-adic Langlands programme for GL2∕Q, Pure Appl. Math. Q. 2 (2006), 279–393.CrossRefGoogle Scholar
Emerton, M., Local-global compatibility in the p-adic Langlands programme for $\text{GL}_{2}/\mathbf{Q}$, Preprint, http://www.math.northwestern.edu/∼emerton/preprints.html.Google Scholar
Emerton, M., Locally analytic vectors in representations of locally p-adic analytic groups, Mem. Amer. Math. Soc., to appear, http://www.math.northwestern.edu/∼emerton/preprints.html.Google Scholar
Fontaine, J.-M., Sur certains types de représentations p-adiques du groupe de Galois d’un corps local; construction d’un anneau de Barsotti–Tate, Ann. of Math. (2) 115 (1982), 529–577.CrossRefGoogle Scholar
Fontaine, J.-M., Représentations p-adiques des corps locaux. I, in The Grothendieck festschrift, Vol II, Progress in Mathematics, vol. 87 (Birkhäuser, Boston, MA, 1990), 249–309.Google Scholar
Ghate, E. and Mézard, A., Filtered modules with coefficients, Trans. Amer. Math. Soc. 361 (2009), 2243–2261.CrossRefGoogle Scholar
Kisin, M., The Fontaine–Mazur conjecture for GL2, J. Amer. Math. Soc. 22 (2009), 641–690.CrossRefGoogle Scholar
Liu, R., Xie, B. and Zhang, Y., Locally analytic vectors of unitary principal series of GL2(Qp), Ann. Sci. Éc. Norm. Supér. (4) 45 (2012), 167–190.CrossRefGoogle Scholar
Nekovar, J., On p-adic height pairings, inSéminaire de théorie des nombres, Paris, 1990–91, 127–202, Progress in Mathematics, vol. 108 (Birkhäuser, Boston, MA, 1993).Google Scholar
Paškūnas, V., On the Breuil–Mézard conjecture, Preprint (2012), arXiv:1209.5205.Google Scholar
Paškūnas, V., The image of Colmez’s Montréal functor, Publ. Math. Inst. Hautes Études Sci. 118 (2013), 1–191.CrossRefGoogle Scholar
Schneider, P. and Teitelbaum, J., Banach space representations and Iwasawa theory, Israel J. Math. 127 (2002), 359–380.CrossRefGoogle Scholar
Schneider, P. and Teitelbaum, J., Algebras of p-adic distributions and admissible representations, Invent. Math. 153 (2003), 145–196.CrossRefGoogle Scholar
Sen, S., Continuous cohomology and p-adic Galois representations, Invent. Math 62 (1980/1981), 89–116.CrossRefGoogle Scholar