Article contents
Foliations on unitary Shimura varieties in positive characteristic
Published online by Cambridge University Press: 11 October 2018
Abstract
When 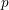 $p$ is inert in the quadratic imaginary field
$p$ is inert in the quadratic imaginary field 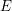 $E$ and
$E$ and 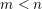 $m<n$, unitary Shimura varieties of signature
$m<n$, unitary Shimura varieties of signature 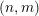 $(n,m)$ and a hyperspecial level subgroup at
$(n,m)$ and a hyperspecial level subgroup at 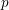 $p$, carry a natural foliationof height 1 and rank
$p$, carry a natural foliationof height 1 and rank 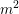 $m^{2}$ in the tangent bundle of their special fiber
$m^{2}$ in the tangent bundle of their special fiber 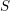 $S$. We study this foliation and show that it acquires singularities at deep Ekedahl–Oort strata, but that these singularities are resolved if we pass to a natural smooth moduli problem
$S$. We study this foliation and show that it acquires singularities at deep Ekedahl–Oort strata, but that these singularities are resolved if we pass to a natural smooth moduli problem 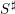 $S^{\sharp }$, a successive blow-up of
$S^{\sharp }$, a successive blow-up of 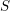 $S$. Over the (
$S$. Over the (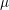 $\unicode[STIX]{x1D707}$-)ordinary locus we relate the foliation to Moonen’s generalized Serre–Tate coordinates. We study the quotient of
$\unicode[STIX]{x1D707}$-)ordinary locus we relate the foliation to Moonen’s generalized Serre–Tate coordinates. We study the quotient of 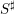 $S^{\sharp }$ by the foliation, and identify it as the Zariski closure of the ordinary-étale locus in the special fiber
$S^{\sharp }$ by the foliation, and identify it as the Zariski closure of the ordinary-étale locus in the special fiber 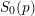 $S_{0}(p)$ of a certain Shimura variety with parahoric level structure at
$S_{0}(p)$ of a certain Shimura variety with parahoric level structure at 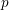 $p$. As a result, we get that this ‘horizontal component’ of
$p$. As a result, we get that this ‘horizontal component’ of 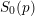 $S_{0}(p)$, as well as its multiplicative counterpart, are non-singular (formerly they were only known to be normal and Cohen–Macaulay). We study two kinds of integral manifolds of the foliation: unitary Shimura subvarieties of signature
$S_{0}(p)$, as well as its multiplicative counterpart, are non-singular (formerly they were only known to be normal and Cohen–Macaulay). We study two kinds of integral manifolds of the foliation: unitary Shimura subvarieties of signature 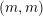 $(m,m)$, and a certain Ekedahl–Oort stratum that we denote
$(m,m)$, and a certain Ekedahl–Oort stratum that we denote 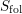 $S_{\text{fol}}$. We conjecture that these are the only integral submanifolds.
$S_{\text{fol}}$. We conjecture that these are the only integral submanifolds.
MSC classification
Information
- Type
- Research Article
- Information
- Copyright
- © The Authors 2018
References
- 2
- Cited by

